基于像差影响的星间角距修正方法

张凯胜，苏秀琴，刘凯

（1 中国科学院西安光学精密机械研究所，西安 710119）

（2 中国科学院大学，北京 100049）

0 引言

星敏感器作为天文导航的一种高精度空间姿态测量设备，是通过对恒星角距的观测获得空间飞行器的姿态［1-3］。目前，星敏感器地面测试主要设备是星模拟器，星模拟器按照工作方式不同分为标定型星模拟器和功能检测型星模拟器。标定型星模拟器结构简单，没有实时性要求，对单星张角、星点位置和星等的模拟精度要求较高［4］；功能检测型星模拟器的核心显示器件是光阀，由于其国内研制水平较低，国外出口的限制制约了星模拟器的发展［5］。因此，球幕投影技术越来越多的在该领域展现出优越性，它不仅能够实现对高精度星敏感器功能的测试，还可以实现复杂光背景下的性能验证测试和动态性能仿真测试［6-7］。

星间角距作为星模拟器的关键技术参数，是衡量其测试精度的重要指标［8］，它是任意两星点之间所存在的角位置关系，其大小取决于各星点位置［9-10］。光学系统作为星模拟器的重要组成部分，其彗差、场曲、像散和畸变均会引起星点位置发生变化，导致由星点位置计算的星间角距与理论星间角距存在差异，影响仿真精度，因此，研究光学系统像差对星间角距的影响是确保星模拟器高精度的重要保障。

本文提出了一种基于光学系统像差影响的星间角距修正方法，即通过分析光学系统像差对星间角距的影响，建立了相应的数学模型并进行了实验验证。

1 球幕投影的星模拟器工作原理及平台设计

1.1 工作原理

球幕投影的星模拟器工作原理如图1 所示，球幕坐标系等比缩放惯性坐标系，球心代表地心，投影仪将星图投射在球幕上，每个星点相对于球心的方位角和俯仰角分别等于其赤经和赤纬。三轴转台坐标系代表卫星坐标系，实时模拟卫星姿态信息。基于卫星时间、主星和目标星的初始轨道参数，进行卫星姿态动力学方程的解算，并将解算后的姿态信息实时传送至三轴转台。同时根据轨道信息和参数进行的高精度轨道递推，完成主星目标星相对位置关系计算，解算出在惯性坐标系下的目标天区指向，实时传输给二轴转台。星敏感器放置在三轴转台上，视轴指向为初始设置值，当启动搜索目标时，按照既定轨道进行搜索，当指向球幕上的投影区时，探测到目标并进行识别。动目标投影仪和恒星投影仪放置在二轴转台上，随着动力学解算出的目标星相对视线角的变化，二轴转台将跟随动力学视线角运动，带动投影仪输出方向发生变化，则投影区在球幕上的位置也发生变化，从而完成对星敏感器全天区、复杂背景下的静态标定和动态性能测试。

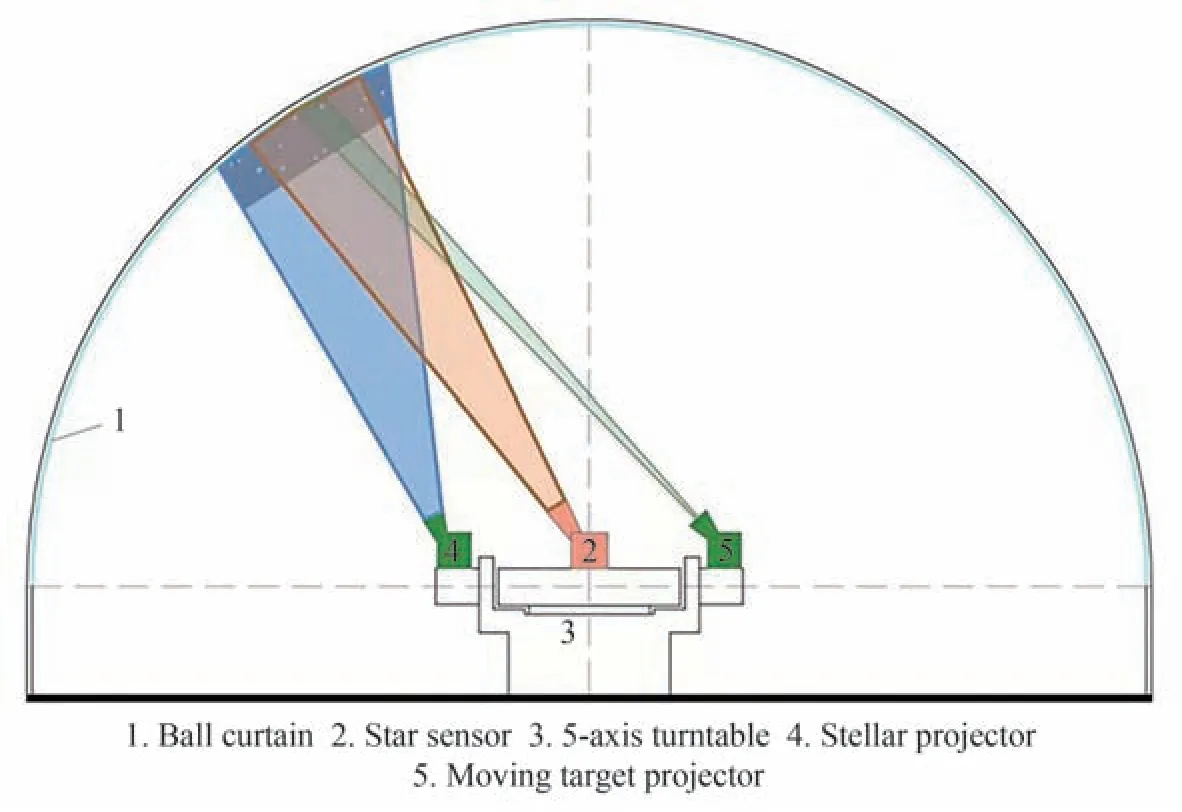
图1 球幕投影的星模拟器原理Fig.1 Schematic diagram of star simulator for spherical screen projection

主星和目标星相对运动示意图如图2 所示，Oi-XiYiZi表示惯性坐标系，Rc为主星地心距矢量，Rt为目标星地心距矢量，r为目标星相对于主星的位置矢量。根据矢量关系有r=Rt-Rc，矢量r指向的天区即是星敏感器看到的天区。根据r的指向查找星图，并根据同一时间太阳、月亮的轨道参数，计算太阳和月亮的位置矢量与视轴矢量关系，经过坐标转换，可得到视场范围内相应的星空背景图像和目标星图像，这个图像输出给投影仪，投影仪将输入的图像投影到球幕上，当星敏感器指向投影区时能够探测到图像，并与其在轨飞行期间看到的图像一致。

图2 主星和目标星相对运动示意图Fig.2 Schematic diagram of relative motion of main star and target star

1.2 平台设计

如图3 所示，该平台主要包括球幕、动目标投影仪、恒星投影仪、五轴飞行转台、图形工作站、实时仿真计算机等。实时仿真计算机根据轨道高度、时间及日期解算当时卫星在轨姿态，为三轴转台和两轴转台及图像生成软件提供输入数据；五轴转台由一个三轴转台和一个与之共轴安装的二轴转台及相关控制柜组成，其中三轴转台与二轴转台独立运行，互不影响，主要用于模拟卫星姿态运动，以完成星体姿态角和角速度的模拟，并根据两星视角关系将投影仪的镜头调整到正确的投影方向上，以确保能够始终看到图像；图形工作站接收来自实时仿真计算机的时间、主星和目标星的轨道参数等数据，根据星敏感器在卫星上的安装矩阵和指向角数据，计算其视场大小，调用图像生成软件，模拟当前视场内的光学图像，并分别送给动目标投影仪和恒星投影仪。将目标星的图像和背景星空的图像投影到球幕上，呈现出恒星背景和目标星图像。

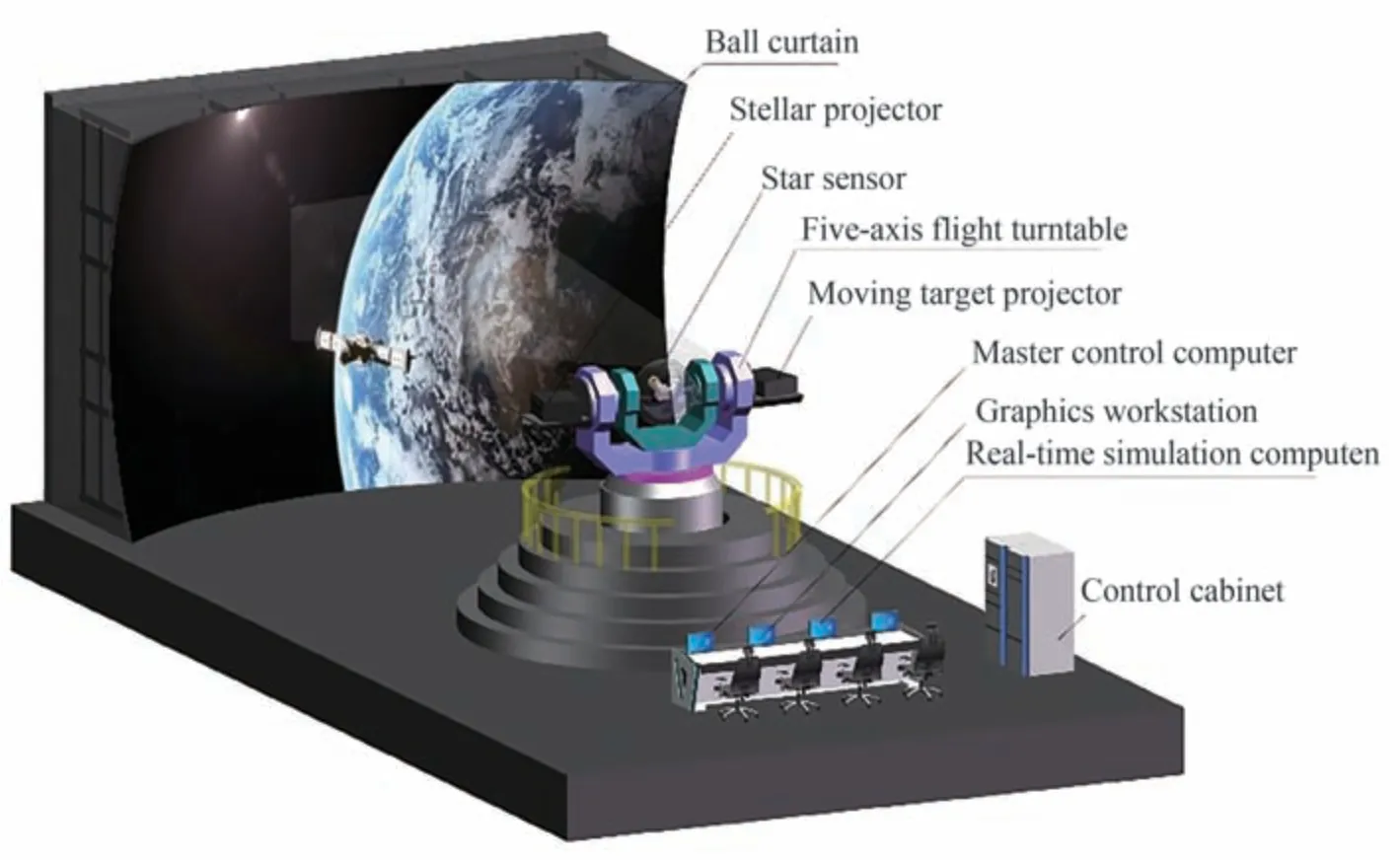
图3 平台设计图Fig.3 Design drawing of platform

2 基于像差影响的星间角距数学模型

2.1 数学模型建立

任意两个星点所确定的角位置关系如图4 所示［11］，星点经过光学系统投射在像面上的坐标关系如图5所示。

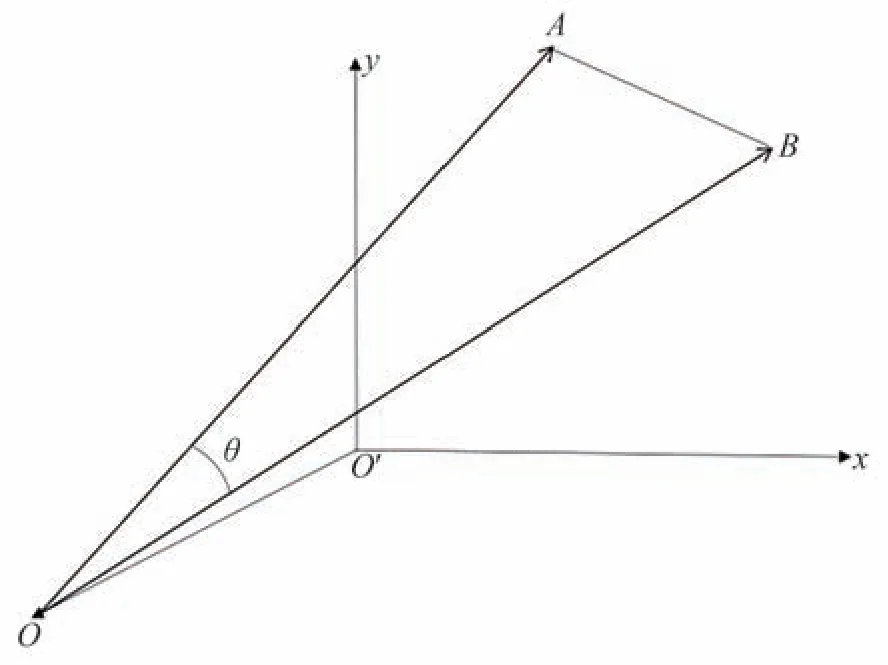
图4 任意两星点间的角位置关系Fig.4 Angular position relationship of two star points

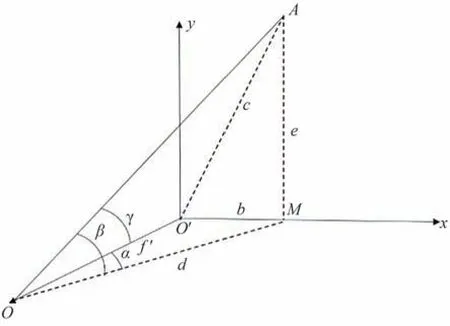
图5 星点在像面上的坐标关系Fig.5 Coordinate diagram of star points on image plane

根据图5 可知

根据图4 和图5 中的几何关系及式（1）～式（5）计算得到两星点之间的星间角距为［12］

星点位置误差是影响星间角距的主要因素，而星点位置误差产生的一个主要的原因是光学系统像差［13-14］，在高精度星模拟器系统中，分析星间角距误差时，不能单纯只考虑畸变一种像差带来的影响，应该综合整个光学系统各类像差带来的星点位置偏移所引起的星间角距误差［13-14］。如图6 所示，对于星点A，在像差影响的情况下，其位置变为A'，图中的位置b，e，c相应的变为b'，e'，c'，方位角α和俯仰角β分别变为α′和β′。对于任意两星点A和B，在像差的影响下，星点A和B的位置分别变为A'和B'，O点相对A'，B'两点的俯仰角分别为，相对A'和B'两点的方位角分别为，相应的b1，e1，c1变为，b2，e2，c2变为，如图7 所示。

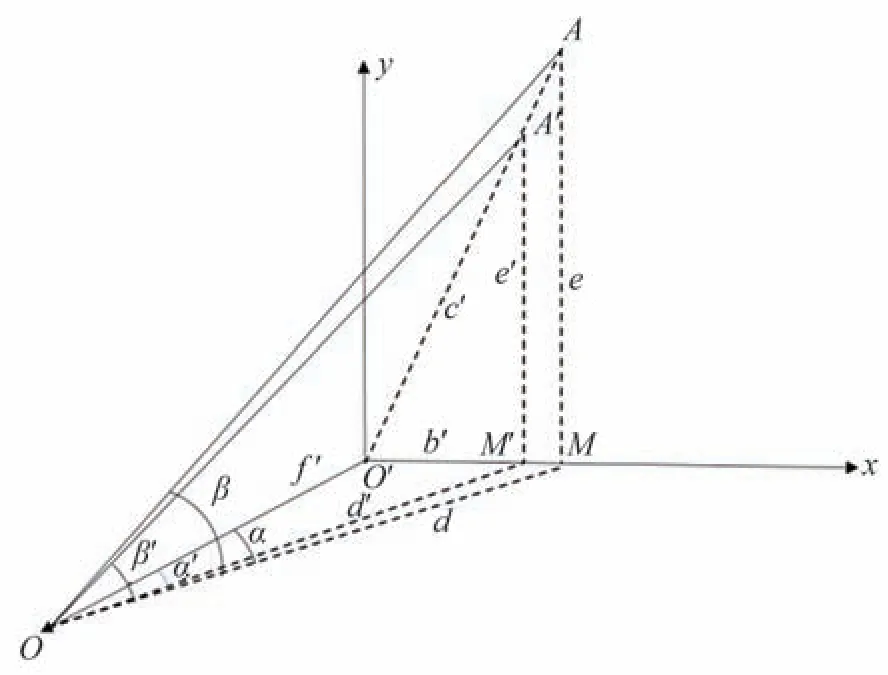
图6 像差对星点位置影响示意图Fig.6 Schematic diagram of influence of aberration on star position

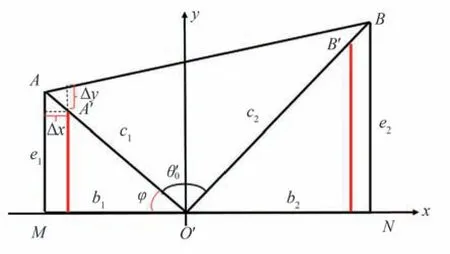
图7 像差对星点星间角距影响示意图Fig.7 Schematic diagram of the influence of aberration on the angular distance between stars

根据图6 可知，各参数之间的关系为

根据图7 可知，像差引起星点A、B位置变化，其偏移量与理想位置的关系可表示为

式中，Δx，Δy是与像差有关的小量，光学系统像差的大小用δy′表示，则有

式中，φ为星点A在x轴上的投影与O′A的夹角，故有

化简式（17）得到

联合式（1）～式（3）及式（15）～式（18）式代入到式（12）和式（13）中化简得到

将式（19）和式（20）代入式（7）和式（9）中化简得到

最终，将式（21）和式（22）代入到星间角距公式中可以得到基于像差的星间角距，即

因此，像差对任意两星点的星间角距的误差为

2.2 光学系统像差影响

在光学系统中，几何像差表示实际光线在理想像平面上的交点与理想位置的差值，其表达式为［15］

式中，δy′，δx′表示光学系统的几何像差，A1，A2，A3，A4，A5分别表示球差、彗差、像散、场曲和畸变系数，h表示光束孔径，y′表示像高。

1）彗差的影响

彗差是轴外物点宽光束像差，式（25）和式（26）中的第二项表示彗差的大小，可以看出，彗差与h2和y′成比例，将式（25）和式（26）中彗差引起的星点横向偏移量代入式（21）和式（22）中得到彗差对方位角α和俯仰角β的影响为

最后将式（27）和式（28）代入式（23）和式（24）中可计算得到彗差对星间角距的影响。

2）场曲和像散的影响

细光束场曲会引起高斯像面的变化，不同视场像高也会随着变化，如图8 所示，场曲引起星点位置的偏移记为δy，则

式中，δy′为细光束场曲的大小，ω为视场角，式（25）和式（26）中的第三项表示场曲和像散的大小。

将式（25）和式（26）中的场曲项代入式（29）得到场曲和像散引起的星点横向偏移为

将式（30）、式（31）中的场曲项代入到式（21）、式（22）中得到细光束场曲对方位角α和俯仰角β的影响，即

将式（30）、式（31）中的像散项代入到式（21）、式（22）中得到像散对方位角α和俯仰角β的影响，即

最后将式（32）～式（35）分别代入式（23）和式（24）中可计算得到场曲和像散对星间角距的影响。

3）畸变的影响

畸变是主光线的像差，根据式（25）第四项得到畸变的横向偏移量，将其代入到式（21）、（22）中得到畸变对方位角α和俯仰角β的影响，即

最后将式（36）和式（37）分别代入式（23）和式（24）中可计算得到畸变对星间角距的影响。

3 像差对星间角距影响的实例分析

3.1 投影光学系统像差

本文以球幕投影的星模拟器平台为例，其投影光学系统参数如表1 所示，光路如图9 所示，投影系统焦距为52.8 mm，投射距离12 m。

表1 投影系统的技术指标Table 1 Technical indicators of projection system

图9 焦距为52.8 mm 光学系统Fig.9 Optical system with focal length of 52.8 mm

该投影系统MTF 如图10 所示，从图中可以看出，MTF 曲线均平滑过渡，在高频93 lp/mm 时，全视场MTF 均大于0.48。不同视场彗差大小可通过彗差和数计算得到，计算得到不同视场彗差大小如表2 所示。

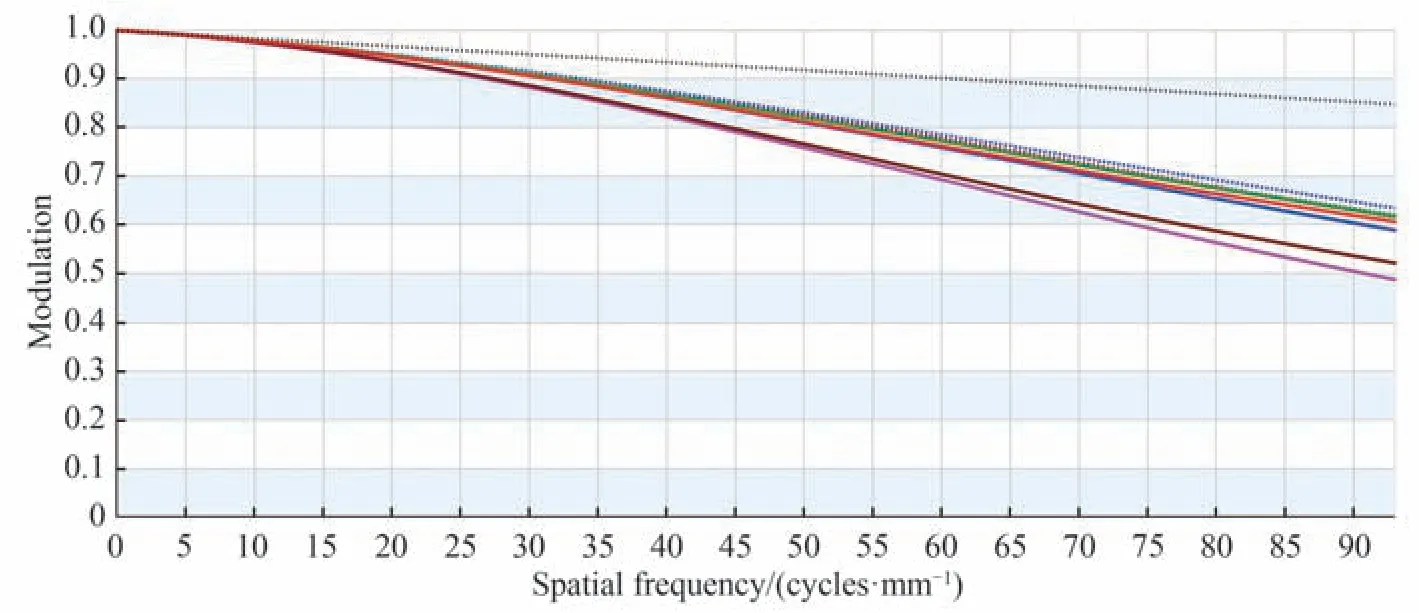
图10 光学系统MTF 曲线Fig.10 MTF curve of optical system

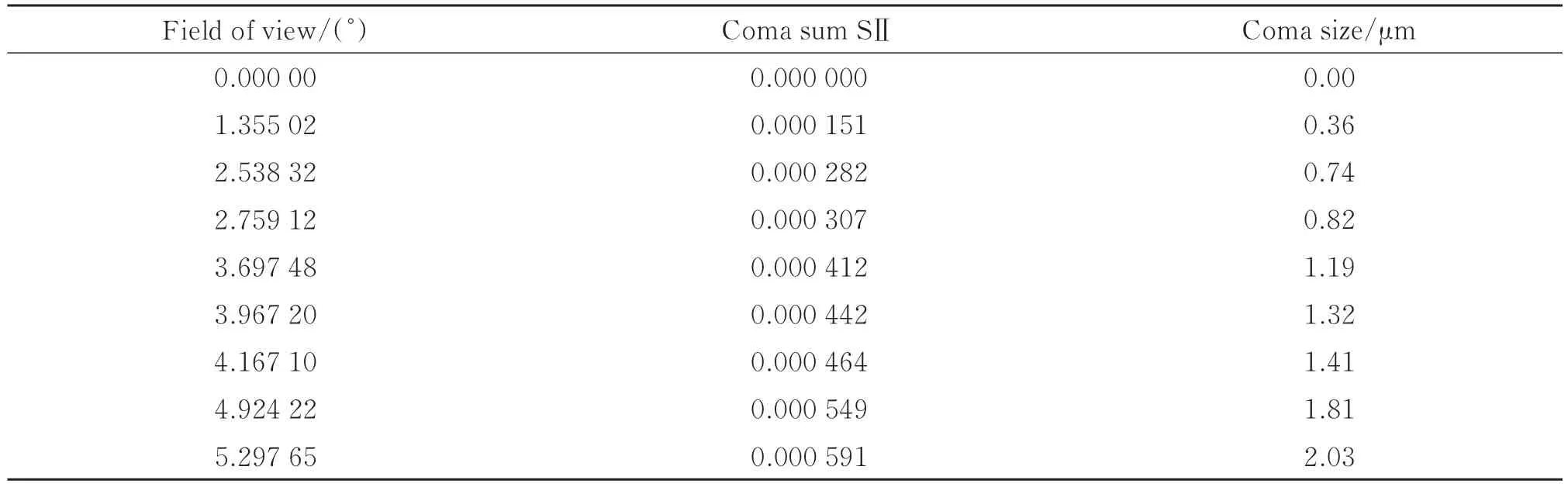
表2 各视场彗差和数及彗差大小Table 2 Coma sum and coma size of each field of view

光学系统场曲、像散和畸变曲线如图11 和图12 所示，从图中可以看出，该投影系统为负畸变，畸变大小为−0.5%。

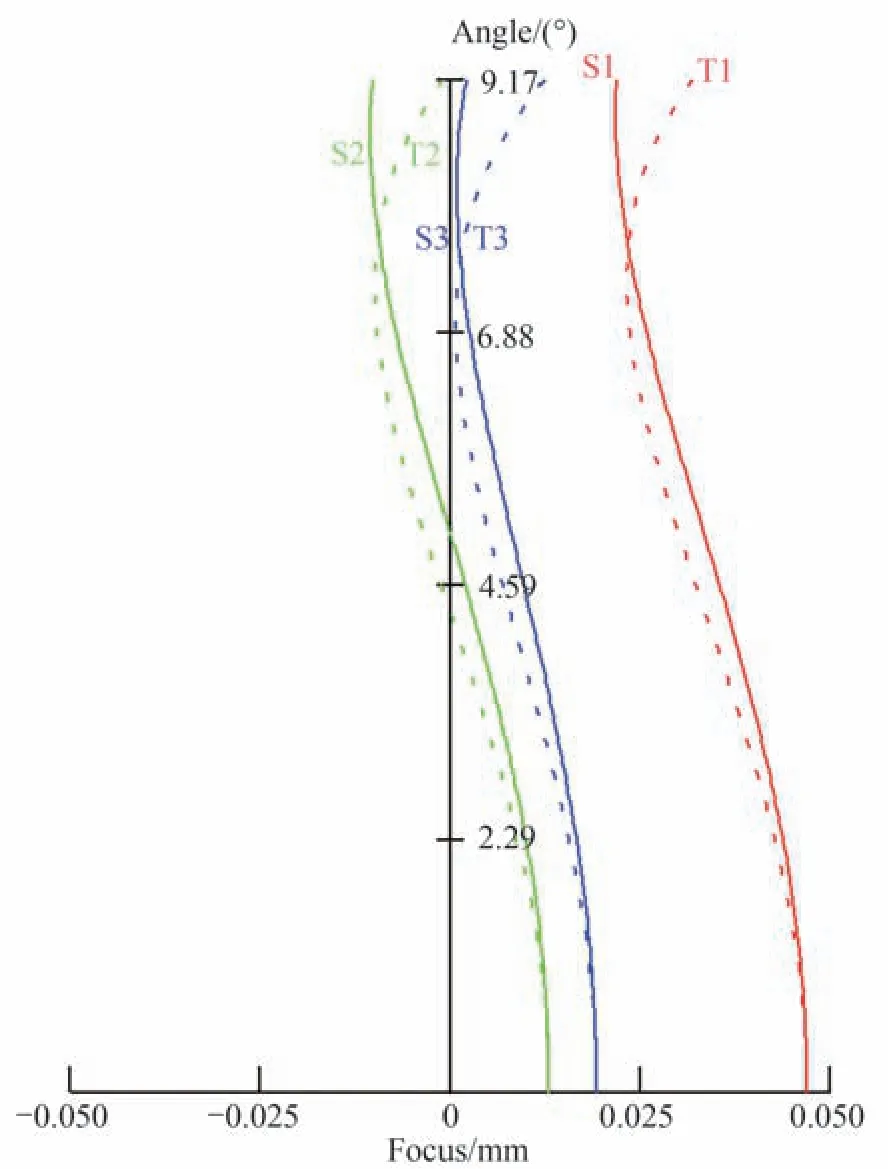
图11 场曲和像散曲线Fig.11 Field & Astigmatism curve

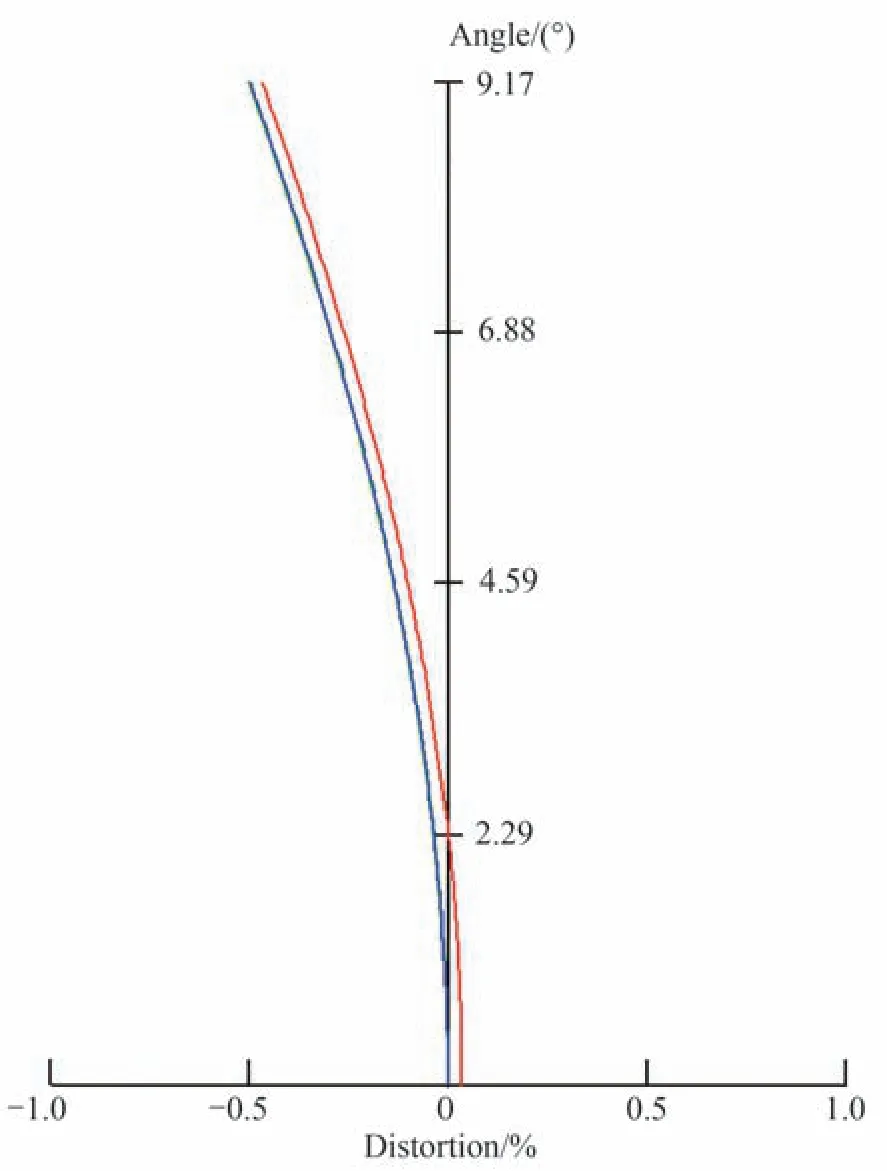
图12 畸变曲线Fig.12 Distortion curve

3.2 结果仿真

软件生成部分星图如图13 所示，该星图中各星点的理论方位角和俯仰角如表3 所示。将该星图中各星点的方位角和俯仰角及其所在视场的像差代入式（27）～式（37）中，计算得到不同像差影响下的各星点的方位角和俯仰角，最后通过式（23）和式（24）计算的到像差对星间角距影响的误差，计算结果如图14 所示。

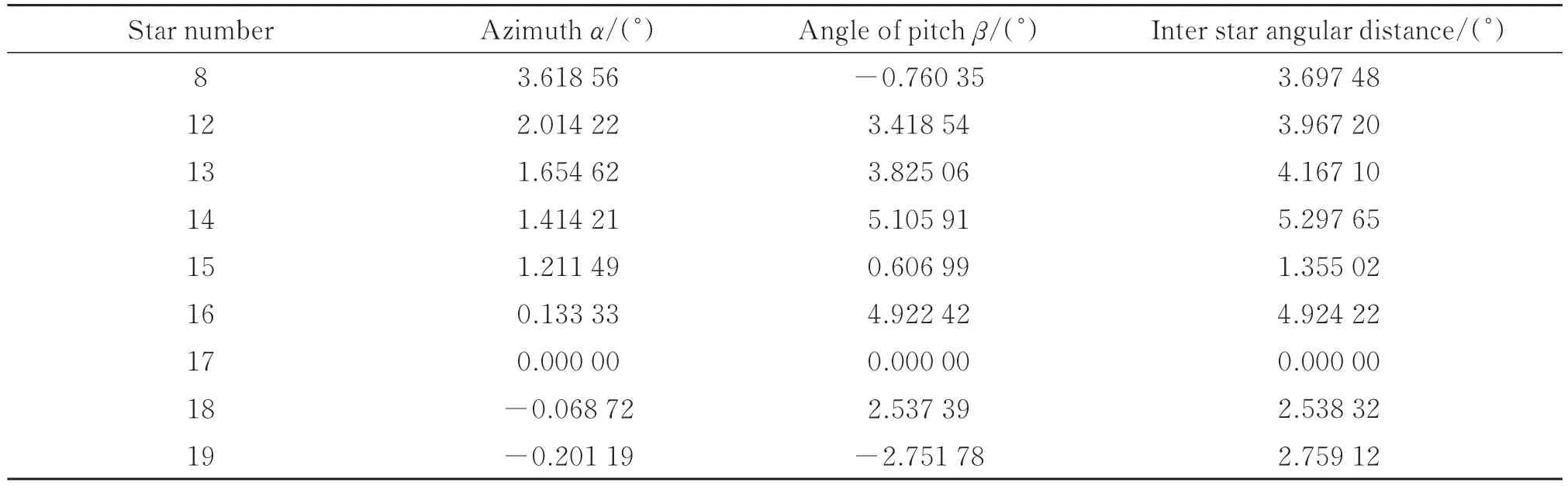
表3 各星点位置Table 3 Positions of stars

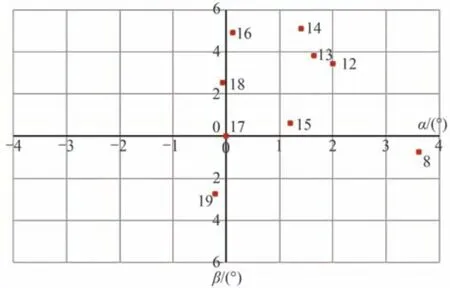
图13 软件生成的部分星图Fig.13 Partial star map generated by software

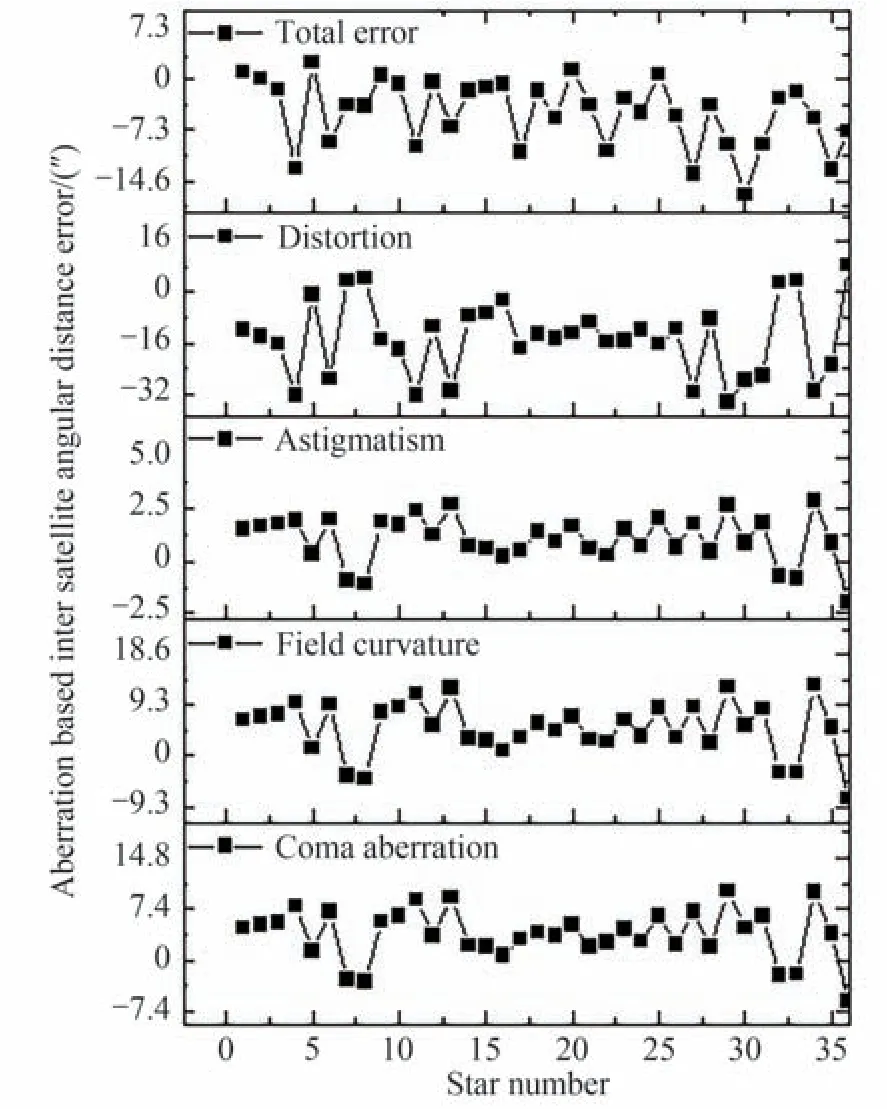
图14 像差对星间角距影响Fig.14 Aberration effect on inter satellite angular distance

由图14 可以看出，彗差对星间角距影响最大为−10.04″，场曲对星间角距最大影响为−13.07″，像散对星间角距影响最大为−2.92″，畸变对星间角距最大影响为34.78″，考虑到各像差对星间角距的补偿性，得到像差对星间角距影响的总误差最大为16.53″。

4 实验验证与分析

4.1 实验验证

球幕投影的星模拟器实物图如图15 所示，软件生成的星图经过光学系统投射到球幕上，通过调整经纬仪高度，使其与中央星点处于同一高度和水平，观测是否能看到全视场内所有星点，采用经纬仪测量球幕上显示的所有待测星点的方位角和俯仰角，如图16 所示，通过测量得到各星点的方位角和俯仰角如表4 所示。

图15 平台实物图Fig.15 Physical drawing of platform

图16 投射星点测试实物图Fig.16 Projection star point test object

表4 各星点实测位置Table 4 Measured position of each star point

通过表4 中测量的方位角和俯仰角计算得到各星之间的星间角距误差如图17 所示，从图中可以看出，实际测试所得的星间角距误差最大为27.56″，而经纬仪的固有误差为0.5″，因此，经纬仪固有误差的影响可忽略不计。

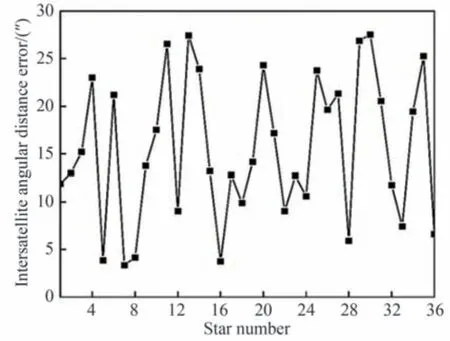
图17 星间角距误差实测值Fig.17 Measured value of inter satellite angular distance error

4.2 误差修正

在星间角距误差修正过程中，首先对视场分辨率大小的区域进行网格分区，本文将水平方向分了6 个区域，将垂直方向分了6 个区域，根据像差大小与所建立的星间角距数学模型，进行多项式曲线拟合，如图18所示。其中，水平灰色区域带里面星点的俯仰角按照水平X坐标和垂直修正量进行拟合，垂直灰色区域带中的星点的方位角按照垂直Y坐标和水平修正量进行拟合。对于交叉区域来说方位角和俯仰角就都进行了拟合，然后以同样的方法对其他区域进行拟合，从而完成整个区域方位角和俯仰角的拟合。

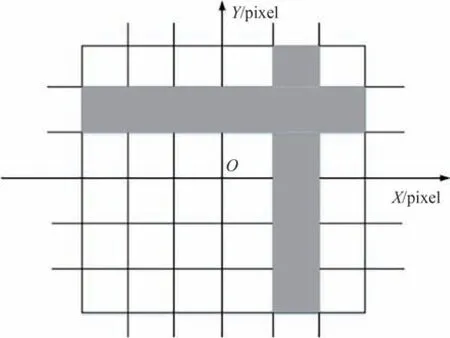
图18 拟合示意图Fig.18 Fitting diagram

结合所建立的星间角距数学模型，针对各星点的方位角和俯仰角进行曲线拟合，得到各星点位置误差拟合曲线如图19 所示。其中，像差x向对方位角影响的拟合曲线方程为

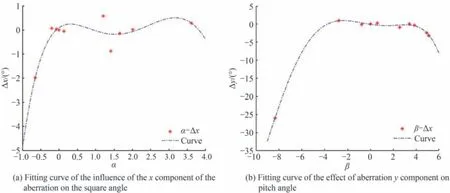
图19 像差对方位角影响的拟合曲线Fig.19 Fitting curve of coma effect on azimuth

像差y向对俯仰角的拟合曲线方程为

根据式（38）和式（39）可得到星点位置误差与方位角和俯仰角的关系，代入下式中计算得到修正后方位角和俯仰角的大小。

式中，Δx和Δy可从拟合曲线中得到，a和b是星点的理论位置，f是焦距，αi和βi是测量得到的方位角和俯仰角，s为像素大小，α0i为各星点与中央星点的方位角。修正后各星点方位角和俯仰角如表5 所示，修正后星间角距误差如图20 所示，结果表明，修正后星间角距最大误差为16.96″，相对于修正前（27.56″）减小了10.60″。

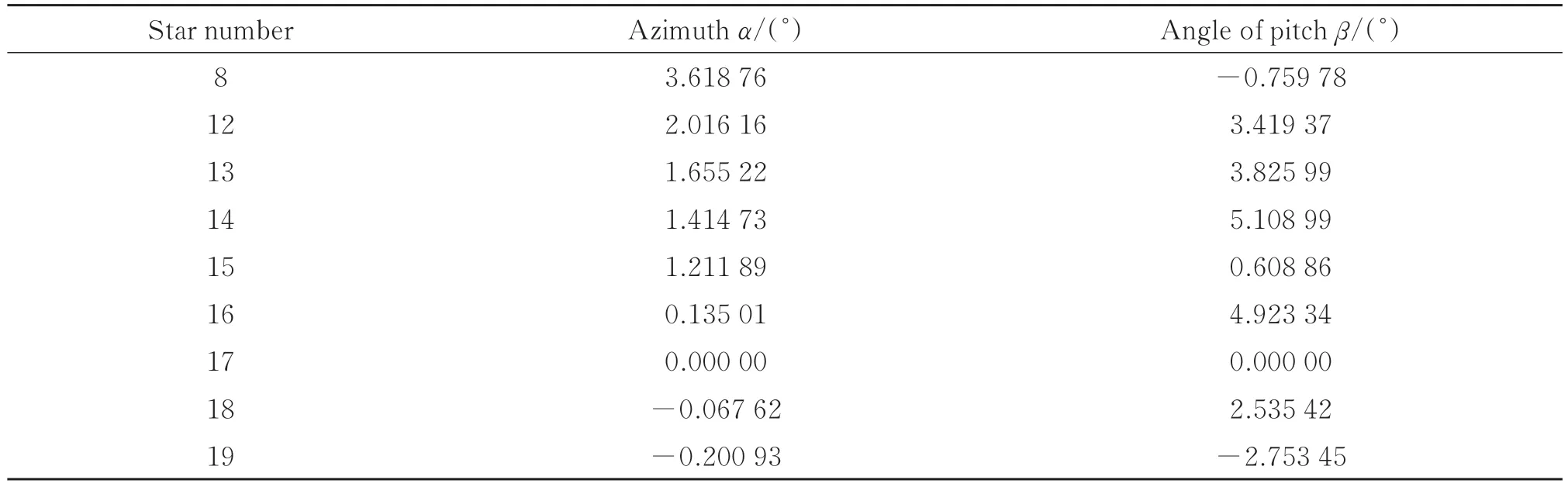
表5 修正后各星点位置Table 5 Position of star points after correction

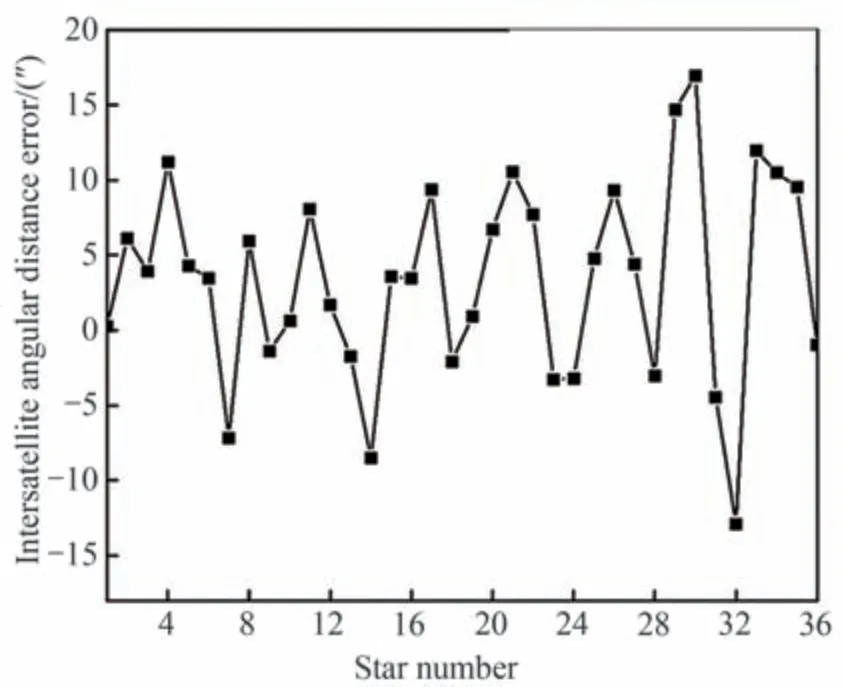
图20 修正后星间角距误差Fig.20 Corrected inter satellite angular distance error

5 结论

针对经典星间角距数学公式没有考虑像差影响的问题，提出了一种基于光学系统像差影响的星间角距修正方法，建立了相应的星间角距数学模型。以球幕投影的星模拟器平台为例，分析了不同像差对星点位置的影响，通过对该实例中各星点之间的星角距进行测量，结合所建立的星间角距数学模型，完成星间角距的修正，从而有效地提高了星模拟器的仿真精度。