星载光电跟瞄转台动态特性分析
2023-08-21彭加力阮萍谢友金李治国王佳浩韩璟宇
彭加力,阮萍,谢友金,李治国,王佳浩,韩璟宇
(1 中国科学院西安光学精密机械研究所,西安 710119)
(2 中国科学院大学,北京 100049)
(3 中国科学院空间精密测量技术重点实验室,西安 710119)
0 引言
星载光电跟瞄转台是一种空间光电载荷,用以在干扰因素复杂的空间环境中实现系统光轴的稳定及对目标的跟踪,广泛应用于空间观测和激光通信等领域,是光电测控领域的重要单机装备[1-5],美国天基空间目标监视(Space-Based Space Surveillance, SBSS)系统,日本(Optical Inter-orbit Communications Engineering Test Satellite, OICETS)卫星上搭载的(Laser Utilizing Communication Equipment, LUCE)激光通信终端以及我国探月工程中的极紫外相机(Extreme Ultraviolet Camera, EUVC)等均使用了星载光电跟瞄转台[6-9]。
在发射过程中,星载光电跟瞄转台受运载火箭产生的加速度动载荷作用,转台及光电载荷将会产生不同程度的振动响应, 响应大小与动载荷量级成正比。当激励频率与系统本身固有频率接近时,将会产生共振现象,响应被放大,由于系统存在一定的阻尼,响应不会至无穷大,但过高的响应放大依旧会对光学系统的工作性能、精度、效率、寿命、安全性和可靠性等产生直接影响。因此分析星载光电跟瞄转台的动态特性,确定系统固有频率及响应,对光机系统的设计以及环境试验的实施具有重要指导作用。
工程中往往通过有限元方法获取转台动态特性,因而建立能够准确反映转台刚度和阻尼特性的有限元模型是准确分析固有频率及响应特性的关键。转台刚度特性由材料、构件的截面以及各构件连接处的刚度决定,对于确定结构来说,各构件连接部位作为载荷的传递路径,其刚度特性直接影响着转台整体的刚度特性。国内对于星载光电跟瞄转台动态特性的仿真并不少见,但对于连接部位(轴承、锁紧机构)的建模容易失真。轴承建模方面,张永强等[10]保留轴承实体,基于Hertz 接触理论进行了轴承参数化建模,由于计算规模极大,该方法一般只在专门对轴承进行研究时才会选择;贺帅[11]利用多点约束单元(Multi Point Constraints, MPC)对二维转台中的轴承进行了刚性等效建模,只保留了轴承绕轴线旋转自由度,其它自由度的刚度无穷大,与实际情况相差较大,只在轴承连接关系对仿真结果影响不大时使用;秦涛等[12]利用两组一维弹簧单元(Spring)分别模拟轴承径向位移刚度和轴向位移刚度,是目前轴承等效建模的主要方法,这种方法能真实反映轴承的位移刚度,但忽略了轴承的角刚度。锁紧机构建模方面的相关研究较少,陈卓[13]去除锁紧机构中爆炸螺栓等结构,锁紧支架和支座利用MPC 单元刚性等效建模,将连接接合面之间的刚度考虑为无穷大,与实际情况相差较大。上述建模方法虽然能在一定程度上等效轴承和锁紧机构,但均存在诸如收敛难度大、建模复杂或连接刚度过大等问题,不能真实反映系统动态特性。
基于上述原因,本文根据某星载光电跟瞄转台的结构组成,提出一种使用广义弹簧单元对轴承和锁紧机构进行等效建模的方法,通过理论计算以及基于模态和扫频试验数据的参数辨识,确定各连接部位的刚度及结构的模态阻尼,分析星载光电跟瞄转台动态特性。
1 星载光电跟瞄转台建模
1.1 转台结构组成
星载光电跟瞄转台主要包括载物台及光电负载、方位轴、俯仰左轴、俯仰右轴、U 型架和锁紧机构等,总体结构如图1 所示。

图1 星载光电跟瞄转台总体结构Fig.1 Overall structure of space electro-optical tracking and pointing turntable
U 型架是连接俯仰轴系和方位轴系的主体,既是俯仰轴系的支撑结构,又固连于方位轴系;方位轴系采用一对背靠背安装的角接触球轴承,用于承受各向载荷;俯仰轴系两端轴承采用一端固定一端游动的安装方式,左轴为固定端,选用一对背靠背安装的角接触球轴承;右轴为游动端,选用深沟球轴承,实现温度补偿;光电负载依靠U 型架结构来支撑和驱动,实现绕方位轴和俯仰轴的旋转;锁紧机构是星载光电跟瞄转台的重要组成部分,在发射过程中锁紧,抑制轴系旋转并且提供辅助支撑,提高整体刚度,入轨运行后解锁,释放转台转动自由度。
1.2 轴系及锁紧机构等效建模
采用广义弹簧单元(Bushing)对跟瞄转台中的轴承和锁紧机构进行等效建模。Bushing 单元又称衬套单元,是一种三向弹簧-阻尼单元,常用于绳索和柔节等多自由度结构的建模[14-16],至多具有6 个自由度,包括3 个主方向的平动和转动,如图2 所示。
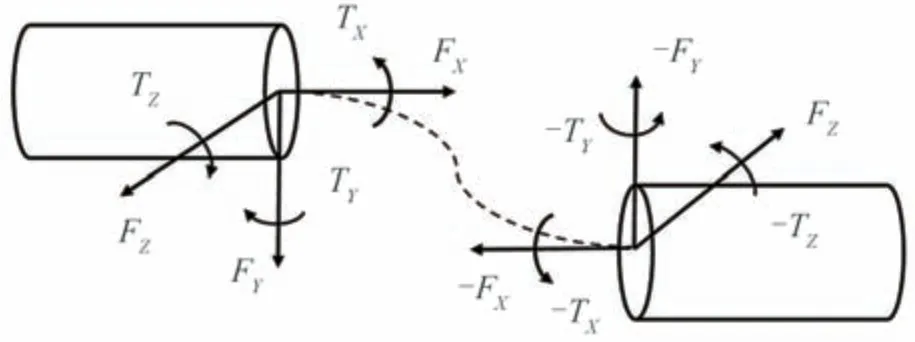
图2 Bushing 单元力学模型Fig. 2 Mechanical model of the Bushing element
Bushing 单元提供一个6 阶刚度矩阵,通过调整刚度矩阵中的参数,可以起到抑制或释放对应自由度运动的作用,模拟单元内部的刚度分布,其刚度矩阵表述为
式中,kx、ky、kz表示三个主方向的位移刚度,kθx、kθy、kθz表示三个主方向的角刚度,其余各项为各自由度刚度的耦合[17]。为简化分析,忽略耦合项,式(1)简化为
1.2.1 轴系等效建模
轴系结构复杂,主要包括电机、主轴、轴承和谐波减速器等部件,结构如图3 所示。其中谐波减速器和轴承的刚度对系统动态特性影响较大。

图3 轴系结构设计剖面图Fig.3 Shafting structure design section
谐波减速器作为传动减速装置,只具有绕旋转轴的角刚度。轴承通常只考虑轴向位移刚度与径向位移刚度,但在实际工作中,滚子往往承受径向、轴向和力矩载荷的联合作用,内外滚道之间产生轴向相对位移δa,径向相对位移δr以及相对角位移θ,如图4 所示。对应于相对位移,轴承具有径向位移刚度、轴向位移刚度、径向角刚度[18]。径向位移刚度一般各向一致,径向角刚度则与实际结构及安装情况有关。

图4 径向、轴向和力矩载荷联合作用下轴承相对位移Fig.4 Relative displacement of inner-outer rings under the combined action of radial, axial and moment loads
假设轴系轴向为Z,则在轴系刚度矩阵式(2)中的kx、ky代表轴承径向位移刚度,kz代表轴向位移刚度;kθx、kθy代表径向角刚度;轴承本身轴向自由旋转,即kθz应为0,但谐波减速器使得轴系又具有一定的轴向角刚度。
1.2.2 锁紧机构等效建模
锁紧机构由锁紧支架、锁紧支座以及火工螺栓组成。其结构与普通螺栓类似,火工螺栓贯穿锁紧支架和支座,在预紧力作用下形成一对结合面。动载荷作用时,结合面间存在法向接触力FN和切向摩擦力FT,各方向有滑移、分离、翻转等趋势[19],如图5 所示。

图5 锁紧机构力学模型Fig.5 Mechanical model of the locking devices
假设爆炸螺栓轴向为Z,则在锁紧机构刚度矩阵式(2)中,kx、ky和kz分别代表锁紧机构三个主方向的位移刚度,表征动载荷作用下结合面间各方向的分离趋势;kθx、kθy和kθz分别代表锁紧机构三个主方向的角刚度,表征动载荷作用下结合面绕各方向的翻转趋势。
简化轴系,去除电机、谐波减速器等构件,只保留主轴和U 型架,分别建立方位轴、俯仰左轴及俯仰右轴共3 个Bushing 单元,简化建模过程中导致的质量缺失,通过0 维质量单元(Point Mass)补足,如图6 所示。

图6 轴系Bushing 单元Fig.6 Bushing element of shafting
简化锁紧机构,去除火工螺栓,只保留锁紧支架和支座,分别建立俯仰锁紧机构及4 个方位锁紧机构共5 个Bushing 单元,如图7所示。
简化其它结构,去除不必要的构件以及倒圆角、孔等特征。除轴承和锁紧机构外,其它各构件连接处均使用刚性连接处理。方位轴座和方位锁紧支座底部约束,最终建立的有限元模型质量为49.5 kg,接近真实质量。节点数为98 万,网格数为64 万,有限元模型如图8 所示。

图8 星载光电跟瞄转台有限元模型示意图Fig.8 Finite element model of space electro-optical tracking and pointing turntable
2 跟瞄转台刚度特性分析
通过轴承刚度理论计算和基于多工况模态试验数据的参数辨识,获取各Bushing 单元的刚度矩阵。
2.1 轴承刚度理论计算
方位轴和俯仰左轴的角接触球轴承,通过预紧消除游隙,提高轴系的刚度以及旋转。角接触球轴承同时承受径向载荷和轴向载荷,对轴承进行受力平衡分析,得到预紧力作用下的角接触球轴承的位移刚度为[10,20]
式中,kx,y为径向刚度,kz为轴向刚度,Dw为滚子直径,Z为滚子数,α为接触角,Fa为轴向预紧力。
由于左右轴承间支承跨距较大,俯仰左轴角接触球轴承具有一定径向角刚度,根据右轴径向位移刚度推导得出
式中,kθx,θy为左轴径向角刚度;kr为右轴径向位移刚度;l为俯仰轴系支承跨距。
右轴的深沟球轴承径向悬空布置,其静刚度为0,但在承受动载荷时,轴承外圈与负载压紧,轴承实际具有一定动刚度。这种动载荷下深沟球轴承的刚度特性目前尚未有文献进行深入探讨,往往通过工程经验给出刚度值。
通过理论计算并结合工程经验,给出轴承刚度部分参数如表1,其余难以理论计算的刚度参数利用多工况的模态试验数据,进行模型参数辨识得出。

表1 轴承刚度矩阵计算值Table 1 Bearing stiffness calculation results
2.2 模态试验设计
模态试验采用德国M+P International 公司的32 通道数据采集系统和Smart Office Analyzer 数据处理分析软件进行,试验现场如图9 所示。试验采用锤击法,按结构划分测点,使用10 个量程为50g(g为重力加速度)的加速度传感器,分4 个批次采集结构上选定的40 个测点的振动响应信号。

图9 星载光电跟瞄转台模态试验Fig.9 Modal test of space electro-optical tracking and pointing turntable
模态试验前6 阶固有频率及振型描述如表2,振型如图10 所示。

表2 模态试验前6 阶固有频率Table 2 The first six natural frequencies of modal test

图10 模态试验前6 阶振型图Fig. 10 The first six mode shapes of modal test
为单独分析各锁紧机构及轴系对整体刚度的影响,根据锁紧机构的不同状态,设置表3 所示3 种试验工况。通过将各振型的仿真固有频率与试验固有频率匹配,得出影响各阶振型的刚度参数。
结合地面调查、物探、钻探验证等工作,可以看出,治理区的地下采空区主要为侯家镇镇办企业采矿形成的采空区,规模较小,形态特征比较规则。采空区分布于I-1号矿脉以北约5~35m范围,东西长约170m。

表3 模态试验工况Table 3 Modal test setting
2.3 基于模态试验数据的刚度参数辨识
2.3.1 俯仰轴系刚度辨识
工况1 中俯仰锁紧机构解锁,光电负载绕俯仰轴旋转只由俯仰谐波的角刚度决定。即俯仰左轴刚度参数kθz决定光电负载绕俯仰轴旋转阶振型固有频率,根据工况1 试验结果,试算确定kθz=4×105N·mm/°,试验与仿真结果如表4。

表4 俯仰轴系刚度辨识Table 4 Stiffness identification of pitching shafting
2.3.2 方位轴系刚度辨识
工况1 中方位锁紧机构解锁,转台只靠方位轴系支撑,转台的左右摆动、前后摆动以及绕方位轴旋转均由方位轴系的角刚度决定。即方位轴系刚度参数kθx决定转台左右摆动阶振型固有频率;kθy决定转台前后摆动阶振型固有频率;方位谐波角刚度kθz决定转台绕方位轴扭转阶振型固有频率。根据工况1 试验结果,试算确定kθx=2.5×107N·mm/°,kθy=4.5×107N·mm/°,kθz=5.5×105N·mm/°,试验与仿真结果如表5。

表5 方位轴系刚度辨识Table 5 Stiffness identification of azimuthal shafting
2.3.3 俯仰锁紧刚度辨识
工况2 在工况1 的基础上,俯仰锁紧机构处于锁紧状态,单独分析俯仰锁紧刚度。光电负载绕俯仰轴旋转、转台的前后摆动以及左右摆动均由俯仰锁紧刚度决定。即俯仰锁紧刚度参数kx决定转台前后摆动阶振型固有频率;ky和kθz决定转台左右摆动阶振型固有频率;kz和kθy决定载物台绕俯仰轴旋转阶振型固有频率。根据工况2的试验结果,试算确定kx=50 000 N/mm,ky=50 000 N/mm,kz=30 000 N/mm,kθy=3×107N·mm/°,kθz=3×107N·mm/°,试验与仿真结果如表6。

表6 俯仰锁紧刚度辨识Table 6 Stiffness identification of pitching locking devices
2.3.4 方位锁紧刚度辨识

表7 方位锁紧刚度辨识Table 7 Stiffness identification of azimuth locking devices
通过理论计算及模型参数识别,最终得到各Bushing 单元刚度矩阵如表8。

表8 各Bushing 单元刚度Table 8 The stiffness coefficient of each Bushing elements
分别采用Bushing 单元对锁紧机构和轴系等效建模(仿真1),采用MPC 单元对锁紧机构和轴系等效建模(仿真2),采用MPC 单元对锁紧机构等效建模,Spring 单元对轴系等效建模(仿真3),模态仿真及试验结果对比如表9。
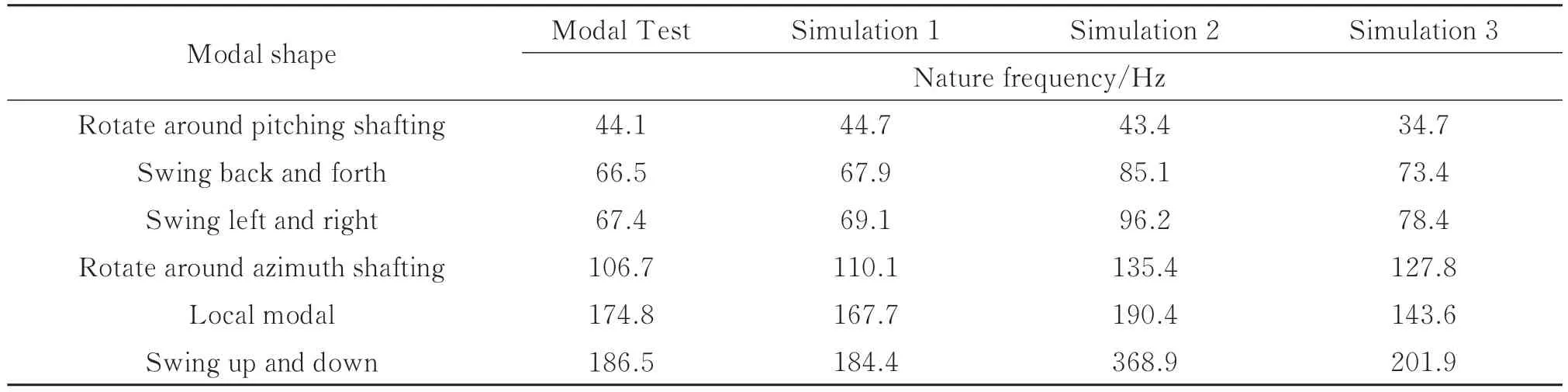
表9 仿真与试验固有频率对比Table 9 Comparison of nature frequency between simulation and modal test
对比上述仿真和试验结果可得:Bushing 单元等效建模能准确反映结构动态特性,固有频率与振型匹配度高,如图11 所示。仿真2 中使用MPC 单元等效锁紧机构和轴系,连接刚度过大,各阶固有频率均高于模态试验结果,尤其转台沿着方位轴上下摆动阶固有频率偏差过大,建模失真严重。相比于仿真2,仿真3 中轴系采用Spring 单元等效建模,各阶固有频率有一定降低,能在一定程度上反映结构动态特性,但仍与模态试验结果有较大偏差。

图11 仿真分析前6 阶振型图Fig.11 The first six mode shapes by modal test
3 跟瞄转台阻尼特性分析
阻尼作为结构动态特性的基本参数,对固有频率影响很小,但会抑制共振频率处的响应幅值。有限元分析中常用的阻尼形式为恒定阻尼(Constant Damping),即每个频率对应的阻尼比都是恒定的,通常取0.01~0.05,但在实际转台振动试验中,阻尼往往随频率非线性变化。直接模态阻尼(Modal Damping)是与频率相关的函数,通过定义对应于每阶振型的阻尼,抑制对应频段响应。由于阻尼效应是叠加的,在恒定阻尼比取0.02 的基础上,通过扫频试验的数据对各阶模态阻尼进行辨识,分析跟瞄转台的阻尼特性。
带工装夹具的转台固定在振动台上,试验采用四点平均控制,即用安装在试验夹具上表面的四个传感器频响测量值的平均值控制振动台激励,8 个三向加速度传感器粘接在转台不同位置,输入条件如表10,试验现场及测点如图12 所示。

表10 0.2 g 正弦扫频试验条件Table 10 Test condition of 0.2 g swept-sine vibration test

图12 扫频试验测点图Fig.12 Measurement points in swept-sine vibration test
扫频试验响应曲线如图13 所示,与第2 节中Bushing 单元模型有限元分析结果对比如表11,试验结果与仿真结果一致性良好,最大相对误差为5.1%,在误差允许的范围内,验证了连接部位刚度特性分析的准确性。
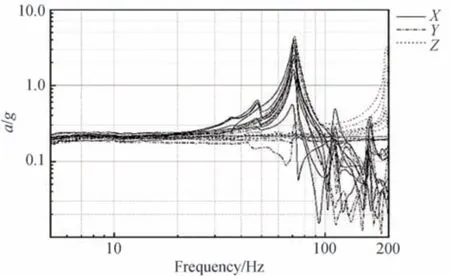
图13 0.2 g 正弦扫频试验曲线Fig.13 0.2 g swept-sine vibration test curve

表11 0.2 g 扫频试验结果及仿真误差Table 11 0.2 g swept-sine vibration test results and simulation errors
提取响应曲线中X、Y、Z三个主方向上的最大响应及其对应的共振频率,根据最大响应确定系统阻尼参数。取恒定阻尼比为0.02,采样频率为1 Hz,进行谐响应仿真分析,通过调整模态阻尼试算,使对应测点处的响应结果与试验结果匹配,得出2 阶模态阻尼参数为0.015,3 阶模态阻尼参数为0.01,6 阶模态阻尼参数为0.005。代入最终得出的阻尼参数,仿真与试验结果对比如表12,试验响应曲线与仿真响应曲线对比如图14所示。

表12 模态阻尼系数辨识Table 12 Modal damping coefficient identification

图14 试验与仿真响应曲线对比Fig.14 The response curves comparison of test with simulation
图中A1、A6、A8为三个测点的试验响应曲线,a1、a6、a8为三个测点的仿真响应曲线。仿真和试验曲线拟合度较高,三个主方向的最大响应匹配,最大相对误差为3.2%。
5 结论
本文根据某星载光电跟瞄转台的结构组成,建立整机等效有限元模型,对其动态特性进行了研究。使用广义弹簧单元(Bushing)对轴承和锁紧机构进行等效建模,通过理论计算和多工况模态试验数据确定了各连接部位刚度参数,有限元分析固有频率相对误差最大为5.1%,相比于传统建模方法能更准确反映转台刚度特性;通过0.2g正弦扫频试验数据确定了系统模态阻尼,主方向最大响应相对误差最大为3.2%,均在允许的误差范围内,动态特性分析准确。
