挑战“数图形”

数学里的图形太迷人了！虽然我刚刚认识线段、角、三角形、长方形等基本图形，但当这些图形重重叠叠地交错在一起，就能构成一幅美丽又复杂的几何图形。每次看到这些复杂图形，我的大脑就会自主运转，分析各种信息，抽丝剥茧，得到结果。

想准确地数出这类图形中所包含的某一种基本图形的个数，需要仔细地观察，灵活地运用有关的知识和思考方法，掌握规律才能获得正确的结果。

浙江省 许智涵

NO.4  从广州到北京的某次快车中途要停靠8个大站，铁路局要为这次快车准备多少种不同车的车票？这些车票中有多少种不同的票价？

【思路导航】

看到这道题，你是不是想说这道题里没有图形啊？其实这道题是数线段的方法在实际生活中的应用。连同广州、北京在内，这条铁路上共有10个站，共有1+2+3+…+9=45条线段，因此要准备45种不同的车票。由于这些车站之间的距离各不相等，因此，有多少种不同的车票，就有多少种不同的票价，所以共有45种不同的票价。

【练一练】從上海到武汉的航运线上，有9个停靠码头，航运公司要为这条航运线准备多少种不同的船票？

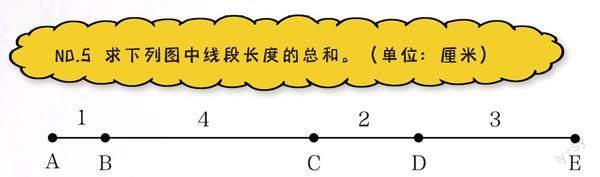
NO.5  求下列图中线段长度的总和。（单位：厘米）

【思路导航】

要求图中的线段长度的总和，可以这样计算：

AB+AC+AD+AE+BC+BD+BE+CD+CE+DE

=1+（1+4）+（1+4+2）+（1+4+2+3）+4+（4+2）+（4+2+3）+2+（2+3）+3

=52厘米。

从上面的计算中可以发现这样一个规律，算式中长1厘米的基本线段（我们把不能再划分的线段称为基本线段）出现了4次，长4厘米的线段出现了（3×2）次，长2厘米的线段出现了（2×3）次，长3厘米的线段出现了（1×4）次。所以，各线段长度的总和还可以这样算：

1×4+4×（3×2）+2×（2×3）+3×（1×4）

=1×（5-1）+4×（5-2）×2+2×（5-3）×3+3×（5-4）×4=52厘米。

上式中的5是线段上的5个点，如果设线段上的点数为n，基本线段分别为a1、a2、…a（n-1）。以上各线段长度的总和为L，那么L=a1×（n-1）×1+a2×（n-2）×2+a3×（n-3）×3+…+a（n-1）×1×（n-1）。

【练一练】一条线段上有21个点（包括两个端点），相邻两点的距离都是4厘米，所有线段长度的总和是多少？