Geogebra软件在高中物理复习课中的应用

宁镇宇 冯洁 李红梅

摘   要：通过常规的绘图工具绘图和理论知识讲解的方式复习平抛运动，学生难以深入理解平抛运动的动态问题和立体空间类型的问题。结合Geogebra应用的复习课，可以将平抛运动的知识点进行归纳总结，通过公式的推导、情境的动态分析和立体空间呈现，将复杂抽象的问题以轨迹图和3 D模型的方式展现出来，帮助学生构建平抛运动的空间模型，降低理解难度，促进学生科学思维的发展。

关键词：Geogebra；平抛运动；复习课

引言

教育部印发的《教育信息化“十三五规化”》指出教育信息化的工作要坚持促进信息技术与教育教学深度融合的核心理念，将信息技术融入到教学和管理模式创新的过程中，以创新促发展，推动教育服务供给方式、教学和管理模式的变革，形成中国特色的教育信息化发展路径；而且随着信息技术与教育教学融合进一步深入，教师信息化教学能力、学生的创新意识、创新能力和信息素养显著提升，养成数字化学习习惯，促进学生的全面发展[ 1 ]。

Geogebra是一套结合几何、代数、数据表、图形、统计和计算的动态数学软件，同时具有处理代数与几何的功能，其功能强大，操作简单[ 2 ]。

将Geogebra软件应用于“平抛运动”的复习课中，可以将平抛运动直观化，激发学生的学习兴趣，促进学生物理观念、科学思维的形成。

1  课前分析

1.1  平抛运动复习课的教学目标

复习课的教学目的是结合考试要求与学生学习中的疑难问题，重新组织教学内容，帮助学生构建系统化的知识结构，通过有针对性的问题分析，暴露学生思维过程中的困惑，进而对知识进行自主重构。

本节复习课的教学目标：利用Geogebra将平抛运动的知识点进行总结归纳，促进学生物理观念的形成；利用Geogebra推导出平抛运动的公式，帮助学生构建物理模型，促进学生科学思维的形成；将Geogebra的3 D模型应用于例题的研究中，帮助学生形成空间立体模型，从而使学生进一步掌握探究和处理问题的能力。

2  结合Geogebra软件的教学过程

2.1 利用Geogebra软件归纳总结

首先在Geogebra软件中画出平抛运动的轨迹，如图1所示；其次通过改变滑动条v0和t，可以发现在Geogebra软件中不论速度和时间如何改变，平抛运动的轨迹始终是一条曲线；最后引导学生复习平抛运动的条件是以一定的初速度v0水平抛出，且只受重力的作用。

接着用Geogebra 软件绘制平抛运动的合运动和分运动图像，体现“一分为二”和“化曲为直”的方法，如图2。在繪制的图中收集数据证据（如表1位移的变化），学生通过数据证据找出平抛运动在水平方向和竖直方向上的运动特点。

观察表中的数据发现，在相等的时间内，水平方向的位移相等，满足水平方向上做匀速直线运动；而在竖直方向上，发现连续相等时间T内下落的高度之差都为10 cm，则满足自由落体运动规律中的？驻Y=gT2，所以物体在竖直上做自由落体运动。

设计意图：在复习课中单纯采用理论知识来讲解平抛运动，过程无趣、呆板，学生不易接受，影响学习效率。结合Geogebra软件来复习平抛运动，一方面可以激起学生学习的兴趣和好奇心，帮助学生巩固知识，构建知识框架；另一方面通过数据证据可以加深学生对平抛运动的理解以及巩固运动学的知识；培养学生科学探究能力。

2.2 利用Geogebra推导公式

平抛运动有两个非常重要的推论：一个是速度偏向角的正切值是位移偏向角的2倍（tanα=2tanθ）；另一个是瞬时速度的反向延长线一定通过此时水平位移的中点[ 3 ]。在以往教学中采用代数关系讲解，过程枯燥抽象，难度较大，学生不易理解。利用Geogebra软件可以将平抛运动的两条推论通过绘图的方式表征出来，它比黑板上绘制的图更加规范，能显示水平位移的中点、距离和速度延长线与X轴交点的坐标，还能证明两条推论在平抛运动的任何位置都成立，增加复习课的趣味性。如图3和图4所示，观察图3发现位移偏向角为53.7°用计算器得出tan（53.7°）=1.361；速度偏向角为69.83°用计算器得出tan（69.63°）=2.722，可以证明位移偏向角和速度偏向角的关系。观察图4发现平抛运动的水平位移OB是120 cm，瞬时速度的反向延长线是I点，OI是60 cm，推出OB等于2倍的OI，可以证明瞬时速度的反向延长线与水平位移的关系。

设计意图：通过Geogebra软件来复习平抛运动的两条推论，可以将平抛运动推论的图像更加直观化，学生易理解，促进学生科学思维的形成。

2.3  Geogebra在例题中的应用

2.3.1 平抛运动中多物体抛出问题

例题1：飞机在水平面上空的某一高度水平匀速飞行，每隔相等时间投放一个物体，如果以第一个物体a的落地点为坐标原点、飞机飞行方向为横坐标的正方向。在竖直平面内建立直角坐标系。如图5所示是第5个物体e离开飞机后，被抛出的5个物体（a、b、c、d、e）在空间位置的示意图，其中不可能的是（     ）。

难点分析：本题的难点是多个物体在相等时间间隔内做平抛运动的落点分析，考察学生对动态分析题目的掌握程度。本题属于平抛运动单点的知识，难度一般。

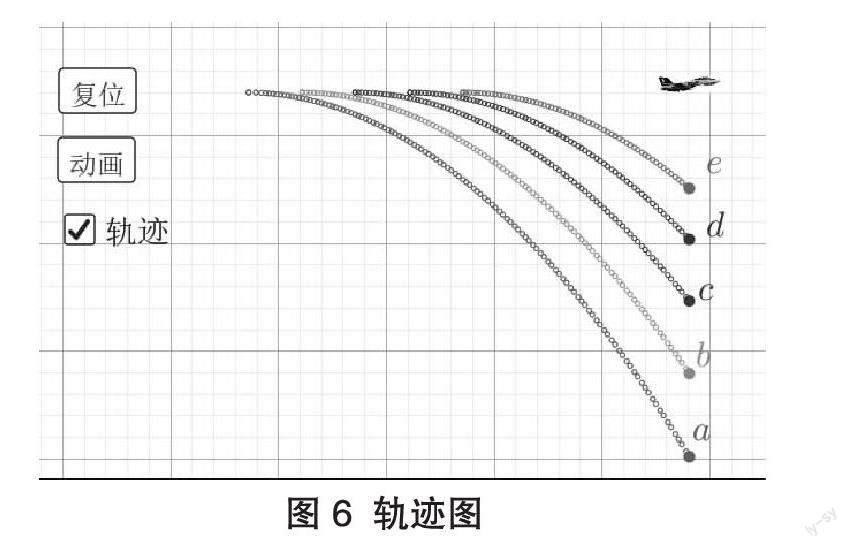
解析：采用Geogebra软件来辅助讲解这道题，首先用软件将四个选项中的图形模拟出来，其次在软件中可以采用动态分析来将物体的运动轨迹描绘出来如图6-9，最后通过运动的轨迹来判断选项中哪个是错误的。观察图6可以看出它和A选项是一致，则A是正确的；观察图7看出它与选项C是一样的落点，则C是正确的；再观察图8，发现它和D选项是一样的落点；则D也是正确的；最终可以判定B选项是不可能存在的。

设计意图：通过Geogebra的辅助，可以将物体的轨迹和落点清晰地描绘出来，将原本固定的点转变为移动的点，这样便于学生更加理解平抛运动的轨迹，而且在理论知识讲解和软件的轨迹分析后，使学生对平抛运动的知识点有更进一步的理解，对今后有关动态分析的题目有了更多的帮助，提高学生的理解能力、推理能力和分析综合能力。

2.3.2 平抛运动中的圆盘问题

例题2：如图10所示，半径分别为R和2R的甲、乙两圆盘固定在同一转轴上，距地面的高度分别为2h和h，两物塊a、b分别置于圆盘边缘，a、b于圆盘间的动摩擦因数μ相等，转轴从静止开始缓慢加速转动，观察发现，a离开盘甲后未与圆盘乙发生碰撞，重力加速度g，最大静摩擦力等于滑动摩擦力，则（    ）。

A.动摩擦因数μ一定大于

B.离开圆盘前，a所受的摩擦力方向一定与速度方向相同

C.离开圆盘落地时，a、b运动的水平位移相等

D.离开圆盘落地时，a、b到转轴的距离相等

难点分析：本题的难点是圆盘在做圆周运动同时物体还在圆盘上做平抛运动，考察学生对物体在两种运动情况下的动态分析，一方面要考虑物体在做平抛运动时的运动过程，另一方面还要考虑圆盘做圆周运动时对物体的影响。属于两种运动结合的题目，难度中等。

解析：从题目中已知甲、乙两个圆盘的角速度相等，在转轴转动后两个物块将做平抛运动且a不会落在乙圆盘上。采用物理方面的知识和结合Geogebra软件来解决该题。

对于A选项，已知圆盘甲做圆周运动，则当a刚好离开圆盘甲时有μmg=m，刚好a离开盘甲后开始做平抛运动，有h=gt2，x=vt；而且还已知a离开盘甲后未与圆盘乙发生碰撞，则可以根据Geogenbra软件画出a点做平抛运动和未与乙碰撞的3 D模型。如图11、12所示，由图中可以观察到x是物块a的水平位移，M点是Ob的中点，则根据勾股定理得出R2+x2≥（2R）2，最终根据三个式子得出μ≥，所以A是正确的。

对于B选项：发现圆盘在做匀速圆周运动，因为题目中说转轴是从静止开始缓慢加速转动，则物块a的速度是围着圆盘运动的切线方向，而物块的摩擦力是与切线方向是相反的，所以B选项不正确。

对于选项C，利用Geogebra画出a、b的运动轨迹图13、14，通过轨迹图，可以利用平抛运动的公式进行解答，当a离开圆盘落地时，有μmg=m当a离开盘甲后做平抛运动有2h=gt2，x1=v1t1则a运动的水平位移为x1=2，利用同样的方法可以得出b的水平位移为x2=2，所以C选项是正确的。

对于D选项：根据软件绘画出的3 D模型进行分析如图15，从图中可以发现a、b到轴的距离是不相等。因为a、b到转轴的距离为L=R2+x，L=（2R2）2+x，所以离开圆盘落地时，a、b到转轴的距离不相等。

设计意图：结合Geogebra软件的3 D模型，可以将物体做平抛运动的轨迹展现出来，并且通过正面和侧面的3 D模型来研究物体的运动状态，可以让学生更加直观化，进而让学生对平抛运动和圆周运动的知识点有了进一步的加强，培养学生的空间思维能力，提高学生解决问题的能力。

2.3.3 平抛运动中临界问题

例题3：一带有乒乓球发射机的乒乓球台如图16所示。水平台面的长和宽分别为L1和L2，中间球网高度为h。发射机安装于台面左侧边缘的中点，能以不同速率向右侧不同方向水平发射乒乓球，发射点距桌面高度3 h。不计空气的作用，重力加速度大小为g。若乒乓球的发射速率v在某范围内，通过选择合适的方向，就能使乒乓球到球网右侧台面上，则v的最大取值范围是（     ）

难点分析：本题的难点是小球在发射过程中，落在什么位置时速度最大或是最小。考察学生对平抛运动的临界问题的掌握程度，本题属于综合型题目，难度大。

解析：该题采用平抛运动的知识和Geogebra的3 D模型进行分析就能得出结果。由题目分析和观察3 D模型图17，可以看出当小球沿中线巧好过网时，速度v最小；而当球落到台面的两个边角速度v最大。由此可以计算在速度最小时有3h-h=时，=vt联立两公式得v1=，当速度最大时有：=vt，3h=gt，联立两式得出v所以D选项正确。

设计意图：通过Goegebra软件绘制出小球在乒乓球桌上的3 D模型，观察小球的落点位置来判断出最大速度和最小速度，进而让学生掌握平抛运动临界问题的知识点，做到对平抛运动知识点的全面应用，培养学生的综合能力和处理问题的能力。

3  总结

在复习课中运用Geogebra软件可以帮助学生将问题和研究的对象更加直观化地表现出来，有利于问题的解决。从而促进学生物理观念、科学思维的形成。另一方面，在Geogebra的辅助功能下，学生对平抛运动的经典例题有更深的理解，对动态分析有了更深入的研究，而且这种可视化教学还可以激发学生学习的兴趣，营造良好的课堂氛围，提高复习课的效率和教学质量。

参考文献：

［1］ 中华人民共和国教育部.教育部关于印发《教育信息化“十三五”规划》的通知[Z].鼓技[2016]2号.

［2］ 肖丽芙.利用GeoGebra辅助物理教学：以高三第一轮“电势”的复习为例[J].中学理科园地，2021，17（4）：73-74，76.

［3］ 刘健智，程婷.GeoGebra软件在物理可视化教学中的应用[J].物理教师，2021，42（6）：70-73.