淹没植被和河床吸收边界对湿地污染物输移影响

方浩泽 杨中华

摘要：湿地是生态系统的重要组成部分，研究淹没植被和河床吸收边界联合作用下的湿地污染物迁移规律可为湿地设计与维护提供参考。采用基于拉格朗日观点的随机位移模型，设置不同的植被密度以及河床对污染物的吸收概率，模拟同时存在密集刚性淹没植被和河床吸收边界的湿地内瞬时释放污染物的输移过程。研究结果表明：河床吸收概率的提升加快了污染物粒子团的平均移动速度并减弱其纵向离散强度，而植被密度的增加会抑制河床对污染物粒子的吸收，使污染物在湿地中的停留时间更长且分布更加分散，从而充分发挥湿地综合净化作用;当吸收概率超过10%后，河床吸收边界可视为完全吸收边界，因此，在湿地设计中不必采用吸收概率更高的基质。

关键词：污染物输移;湿地;随机位移模型;吸收边界;淹没植被

中图分类号：TV131.2

文献标志码：A

文章编号：1001-6791（2023）01-0126-08

收稿日期：2022-08-15;

网络出版日期：2022-11-23

网络出版地址：https：∥kns.cnki.net/kcms/detail/32.1309.P.20221122.1531.002.html

基金项目：国家自然科学基金资助项目（52020105006;51879199）

作者简介：方浩泽（1995—），男，广西南宁人，博士研究生，主要从事环境水力学方面研究。

E-mail：haozefang@whu.edu.cn

通信作者：杨中华，E-mail：yzh@whu.edu.cn

湿地在生态系统中扮演着重要角色^［1］，工业化飞速发展致使含有重金属元素以及氮磷的污染物被排放到自然湿地中，导致自然湿地遭受污染，进而威胁整个生态系统^［2］。与此同时，人工湿地因与传统污水处理厂相比具有投资少、运行成本低等优点，正在人口密度较低的农村地区兴起。研究污染物在湿地中的输移过程可为人工湿地设计与天然湿地维护提供理论参考^［3-4］。

现有研究表明，湿地植被的存在改变了水流结构^［5-7］，而水中的物质迁移受到水流结构的影响。许多学者已针对挺水植被进行了研究，分析其对纵向离散系数以及污染物停留时间分布的影响^［8-9］。而对于淹没植被，Lou等^［10］发现垂向流速分布在其顶部附近出现拐点，但对污染物输移的影响尚不明确。河床的吸收作用也是影响湿地溶质运移的一个重要因素，Guo等^［11］研究發现河床吸收影响了物质的纵向和垂向浓度分布，并导致污染物集中在上层。在瞬时释放条件下，Wang等^［12］指出吸收作用对浓度垂向分布的影响在上下游存在差异。同时考虑淹没植被和河床吸收作用对湿地污染物输移过程的影响更接近湿地实际情况，值得进行更深入的研究。

解析方法的结果一般具有明确物理意义，但考虑到数学推导可行性的限制，解析方法一般会对流动进行一定程度的简化，对于复杂实际情况其结果准确性会受到影响^［4］。原位观测能提供最接近实际情况的数据，但常受到外界条件的干扰，数据精度不高且变量较难控制。室内水槽试验排除外界条件干扰，能提供较为准确的数据，但试验运行存在成本高和时间长的缺点^［10］。数值模拟方法在解析方法或试验的成果基础上形成，在节约成本和时间的同时能得到较为准确的模拟结果，因此许多学者采用数值模拟方法研究污染物输移。研究污染物输移过程的数值模拟方法大致分为两大类：欧拉方法和拉格朗日方法。到目前为止，多数研究都是利用欧拉方法完成的^［13-14］。随机位移模型（RDM）是一种拉格朗日方法，污染物的输移过程是通过大量离散的无质量粒子来模拟的，每个粒子都被单独跟踪，虽然计算成本更高，但结果更加精确^［15］。相对于欧拉方法，随机位移模型具有粒子运动显示直观、源的表示简单、计算区域划分高效以及无数值耗散等优点。考虑到以上优点，许多学者采用随机位移模型来模拟湿地中复杂的污染物输移过程。Lu等^［16］在研究柔性植被流中的污染物输移时，采用了随机位移模型来计算冠层内的离散;槐文信等^［17］利用随机位移模型模拟了部分挺水植被水流中污染物的混合输移，揭示了粒子在横断面的堆积和扩散情况。需要说明的是，由于随机位移模型只描述离散粒子的随流运动，一般适用于模拟不会与水体发生生物化学反应且不会显著改变水流结构的物质，即保守的动力惰性物质或示踪质。

本研究旨在采用随机位移模型研究淹没植被和河床对湿地污染物输移的影响。采用解析解对模型进行验证，设置具有不同植被密度以及河床对污染物吸收概率的7个工况，模拟污染物的输移过程，计算河床对污染物粒子的相对吸收量、污染物粒子团的平均移动速度和污染物粒子团纵向离散强度，探讨淹没植被和河床对湿地污染物输移的影响。

1 模型原理及验证

本研究将模拟限制在立面二维。在这种情况下，物质输运由纵向流速沿垂向不均匀分布引起的纵向随流输运和垂向紊动扩散所主导。随机位移模型属于拉格朗日方法，它追踪每个污染物粒子的运动过程。随机位移模型模拟的污染物粒子的运动由其所在位置的纵向流速和垂向紊动扩散系数决定，如式（1）和式（2）所示^［18］。

式中：x_i为粒子纵向坐标，m;z_i为粒子垂向坐标，m;下标i表示第i时刻;U为纵向流速，m/s;E_z为垂向紊动扩散系数，m²/s;R为一个遵循标准正态分布的随机变量;Δt为时间步长，s。

无河床吸收情况下，为防止粒子移动到水体外，越过水面的粒子将以水面为镜面被反射回水体中，如式（3）所示;低于湿地底面的粒子则以底面为镜面被反射回水体中，如式（4）所示。存在河床吸收的情况下，当粒子接触底面时，生成0～1之间均匀分布的随机数，若其小于等于吸收概率（p_a），粒子被河床吸收;反之粒子被反射回湿地内。

式中：H为总水深，m。

为验证模型及算法的有效性，需模拟无植被且无河床吸收的明渠水流中的瞬时污染排放过程，并采用解析解进行验证。式（5）为垂向有界的剪切流瞬时点源二维紊动扩散解析解。纵向离散系数（K）和断面平均纵向紊动扩散系数

（E_x）采用Elder公式计算^［19］，如式（6）、式（7）所示，假设紊动为各向同性，即断面平均垂向紊动扩散系数E_z=E_x。纵向流速呈对数分布，采用式（8）^［15］计算。明渠总水深固定为1 m，污染物总质量（M）设为3.6 kg，3.6F10⁶个粒子在x=0处、水深0.5 m处一次性释放，每颗粒子质量为1 mg，时间步长取0.01 s。取粒子释放后

1 500 s时刻浓度的沿程分布进行比较，模拟结果如图1所示，随机位移模型模拟结果与解析解基本吻合。

式中：C为质量浓度，kg/m²;t为时间，s;U为纵向流速的断面平均值，m/s;x为纵向坐标，m;z为垂向坐标，m;u_*为摩阻流速，取0.01 m/s;k为卡门常数，取0.41;k_s为粗糙高度，取0.01m。

2 植被和河床吸收作用下的模拟

考虑淹没植被的影响，纵向流速分布和垂向紊动扩散系数分布采用Nepf等^［20］的模型来描述，该模型适用于具有均匀密集刚性淹没植被的流动，视植被ah_v>0.1为密集分布，其中a为单位体积植被迎流面面积，hv为植被高度。纵向流速分布模型分为3个部分，其中边界层主导区和尾流区的流速均匀分布，混合层流速分布如式（9）所示。垂向紊动扩散系数分布模型分为4个部分，如式（10）所示。该模型的准确性和有效性已由Follett等^［21］进行了验证，故本文直接将其应用于模拟中。

式中：U₁为尾流区流速，m/s;U₂为边界层主导区流速，m/s;z₁为尾流区厚度，m;t_ml为混合层厚度，m;ΔU为边界层主导区和尾流区之间的速度差，m/s;d为植被直径，m。

本研究设计了7个工况进行模拟（图2），参考相关水槽试验^［22-23］，总水深、植被直径和底坡（S）分别固定为0.4 m、0.006 m和2F10^-5，植被高度参考矮生苦草（0.1～0.2 m）、光叶眼子菜（0.2～0.3 m）和伊乐藻（0.3～0.35 m）取0.2 m，在x=0处水面一次性释放120 000个粒子，时间步长设为0.05 s。各工况具体模拟条件和参数如表1所示，参数z₁、t_ml、U₁和U₂采用Ghisalberti等^［22］迭代模型获得，该模型在0.016≤ad<0.081内适用。工况1—工况3的河床吸收概率相同，单位体积植被迎流面面积不同，参数值的选取同样参考了相关水槽试验^［22-23］，用以对比分析淹没植被密度变化对污染物运移的影响;工况1、工况4—工况7的单位体积植被迎流面面积相同，河床吸收概率不同，取值范围从0变化至100%覆盖理论上可能出现的所有情况，用以对比分析河床吸收概率变化对污染物运移的影响。每个工况重复模拟5次，结果取平均值。

采用Sankarasubramanian等^［24］提出的3个量纲一参数评价淹没植被和河床吸收对湿地污染物输移的影响，计算公式如下：

式中：K₀为量纲一有效衰减系数，表示河床对污染物粒子的相对吸收量;K₁为量纲一有效速度系数，表示污染物粒子团的平均移动速度;K₂为量纲一有效纵向离散系数，表示污染物粒子团纵向离散强度;为量纲一化的时间;n为湿地内部粒子总数;x为粒子纵向坐标平均值，m;V（x_i）为粒子纵向坐标的方差，m²。

3 結果和讨论

粒子释放后，各工况下3个量纲一参数的值在=1时虽然存在震荡但已基本稳定。如图3（a）所示，在河床吸收概率不变的情况下，K₀的绝对值随着淹没植被密度增大而减小。根据式（11），K₀的绝对值越大表示河床吸收的污染物粒子越多，因此，淹没植被密度降低有助于河床对污染物的吸收。由图3（b）可以发现，河床吸收概率从0变化至10%时，K₀的绝对值大幅度增加，但从10%变化至100%，K₀基本没有变化。这可能是因为依靠垂向紊动扩散到达河床附近的粒子数有限，具有10%吸收概率的河床基本可以全部吸收这部分粒子，而具有更大吸收概率的河床没有额外的粒子可以吸收，所以结果与前者基本相同。此外底部粒子减少表明污染物垂向浓度分布偏离了均匀分布，因此，采用垂向均匀分布可能会在模拟湿地污染物迁移时产生误差。

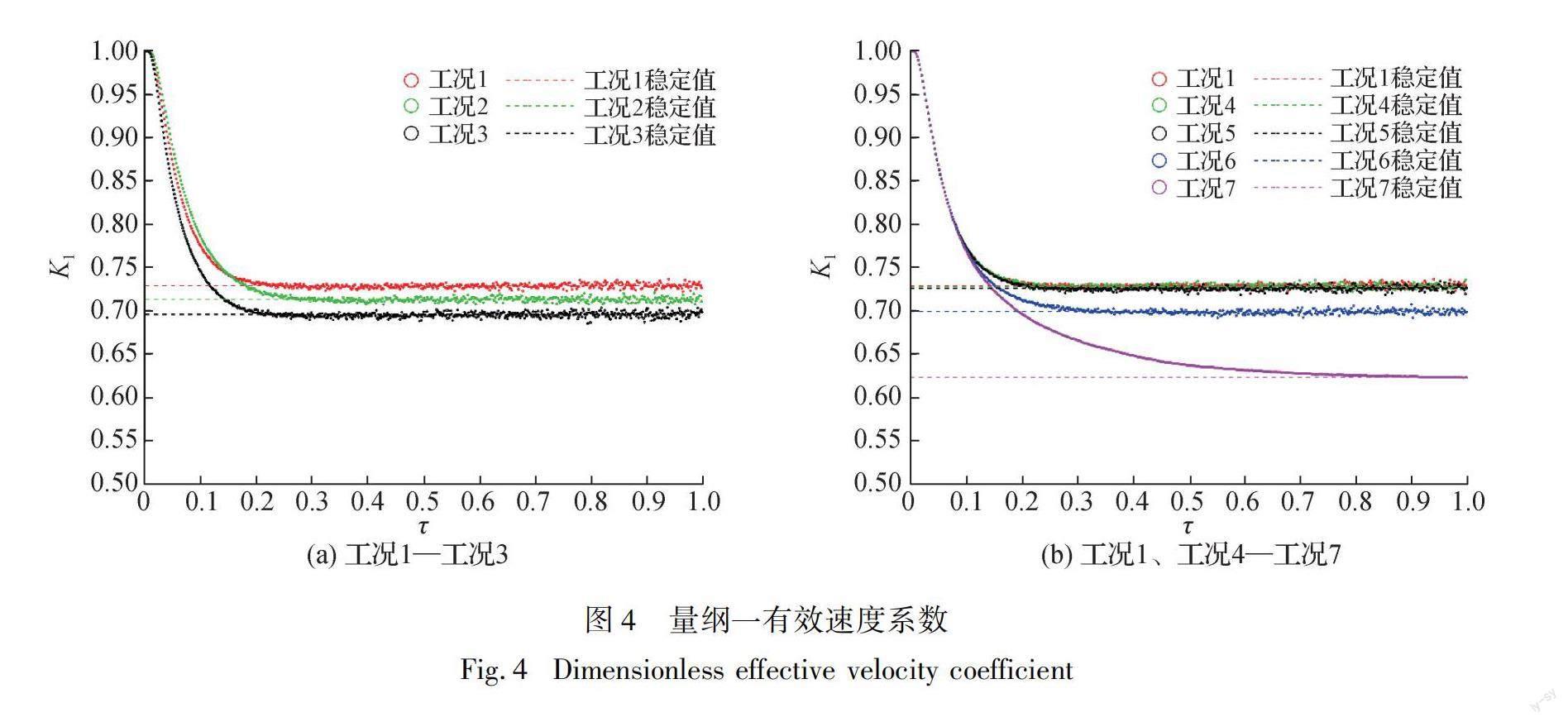
K₁表示污染物粒子团的平均移动速度，由图4（a）可以看出淹没植被密度的增大减慢了粒子团的平均速度移动，使污染物在湿地中的停留时间更长，从而充分发挥湿地净化效果。而在图4（b）中，随着河床吸收概率的提高，污染物粒子团的平均移动速度变快，但类似K₀，吸收概率超过10%以后，平均移动速度的增幅变得很小，这与Wang等^［25］在无植被情况下发现的规律相似。结合纵向流速分布模型分析可知，移动速度较慢的粒子都集中在靠近底面的尾流区，淹没植被密度的减小以及河床吸收概率的提高都会增加慢速粒子的被吸收量，进而提高粒子团的平均移动速度。

由图5（a）可见，K₂随着淹没植被密度的增大而增大，说明浓密的植被会导致更强的纵向离散，使湿地中的污染物分布更分散，避免分布过于集中导致局部区域净化负荷过高。如图5（b）所示，河床吸收概率的提升，使更多靠近河床的慢速粒子被吸收，粒子团在纵向上更加集中，导致纵向离散减小，K₂因此减小。此现象与其他学者^{［24，26］}在存在不可逆一阶吸收边界条件下的理论预测相符，但除此之外，本研究还发现河床吸收概率对纵向离散的影响在超过10%后会变得不明显，因此从高效利用河床对污染物吸收作用的角度出发，在湿地设计和建设中，无需采用吸收概率更高的基质。受随机位移模型原理以及纵向流速模型和垂向紊动扩散系数模型的限制，以上结果仅适用于存在均匀密集刚性淹没植被的湿地中保守的动力惰性污染物，其他湿地条件下不同性质污染物的输移规律有待进一步研究。

4 结论

本研究采用随机位移模型模拟同时存在均匀密集刚性淹没植被和河床吸收边界的湿地内瞬时释放的污染物的输移过程，研究淹没植被和河床吸收作用对湿地污染物输移的影响，得到以下结论：

（1）  河床吸收概率的提升加快了污染物粒子团的平均移动速度并减弱污染物的纵向离散，而植被密度的增加会抑制河床吸收，从而产生相反的影响。采用更密集的淹没植被布置形式能使污染物在湿地中的停留时间更长且分布更加分散，从而更充分发挥湿地的综合净化作用。

（2）  当吸收概率超过10%后，河床吸收边界可视为完全吸收边界。从高效利用河床对污染物的吸收作用的角度出发，在湿地设计和建设中，不必采用吸收概率更高的基质。

参考文献：

［1］CHENG F Y，van METER K J，BYRNES D K，et al.Maximizing US nitrate removal through wetland protection and restoration［J］.Nature，2020，588（7839）：625-630.

［2］TEMMINK R J M，LAMERS L P M，ANGELINI C，et al.Recovering wetland biogeomorphic feedbacks to restore the world′s biotic carbon hotspots［J］.Science，2022，376（6593）：eabn1479.

［3］SARKAR D J，DAS SARKAR S，DAS B K，et al.Occurrence，fate and removal of microplastics as heavy metal vector in natural wastewater treatment wetland system［J］.Water Research，2021，192：116853.

［4］WANG H L，LI S L，ZHU Z T，et al.Analyzing solute transport in modeled wetland flows under surface wind and bed absorption conditions［J］.International Journal of Heat and Mass Transfer，2020，150：119319.

［5］張英豪，赖锡军，张琳，等.风浪作用下水生植物对水流结构的影响：以太湖中两种典型沉水植物为例［J］.水科学进展，2020，31（3）：441-449.（ZHANG Y H，LAI X J，ZHANG L，et al.Influence of aquatic vegetation on flow structure under wind-driven waves：a case study in Lake Taihu （China） with two typical submerged vegetations［J］.Advances in Water Science，2020，31（3）：441-449.（in Chinese））

［6］赵汗青，唐洪武，闫静，等.淹没植物明渠床面冲淤及其对水流运动的影响［J］.水科学进展，2021，32（2）：250-258.（ZHAO H Q，TANG H W，YAN J，et al.Interactions between bedforms and open channel flows through submerged vegetation［J］.Advances in Water Science，2021，32（2）：250-258.（in Chinese））

［7］陆彦，王唯旭，陆永军，等.灌木植被分布区阻力特性理论及试验研究［J］.水科学进展，2020，31（4）：556-564.（LU Y，WANG W X，LU Y J，et al.Theoretical and experimental study on resistance characteristics of shrub vegetation distribution area［J］.Advances in Water Science，2020，31（4）：556-564.（in Chinese））

［8］ZHANG J，HUAI W X，SHI H R，et al.Estimation of the longitudinal dispersion coefficient using a two-zone model in a channel partially covered with artificial emergent vegetation［J］.Environmental Fluid Mechanics，2021，21（1）：155-175.

［9］ZHOU W Z，DONG B，YANG J Z，et al.Correction of residence time distributions and hydraulic indexes affected by tracer release duration in surface flow constructed wetlands［J］.Journal of Hydrology，2021，603：127106.

［10］LOU S，LIU H Z，LIU S G，et al.Longitudinal and lateral diffusion of solute transport in flow with rigid vegetation［J］.Environmental Sciences Europe，2020，32：40.

［11］GUO J L，WU X D，JIANG W Q，et al.Contaminant transport from point source on water surface in open channel flow with bed absorption［J］.Journal of Hydrology，2018，561：295-303.

［12］WANG H L，ZHU Z T，LI S L，et al.Solute dispersion in wetland flows with bed absorption［J］.Journal of Hydrology，2019，579：124149.

［13］WANG J Y，HE G J，DEY S，et al.Influence of submerged flexible vegetation on turbulence in an open-channel flow［J］.Journal of Fluid Mechanics，2022，947：A31.

［14］D′IPPOLITO A，CALOMINO F，ALFONSI G，et al.Flow resistance in open channel due to vegetation at reach scale：a review［J］.Water，2021，13（2）：116.

［15］LIANG D F，WU X F.A random walk simulation of scalar mixing in flows through submerged vegetations［J］.Journal of Hydrodynamics，2014，26（3）：343-350.

［16］LU J，DAI H C.Numerical modeling of pollution transport in flexible vegetation［J］.Applied Mathematical Modelling，2018，64：93-105.

［17］槐文信，梁雪融.基于隨机位移方法的植被水流纵向离散研究［J］.工程科学与技术，2019，51（3）：138-143.（HUAI W X，LIANG X R.Simulation of longitudinal dispersion in vegetated flows based on random displacement model［J］.Advanced Engineering Sciences，2019，51（3）：138-143.（in Chinese））

［18］HOTEIT H，MOS R，YOUNES A，et al.Three-dimensional modeling of mass transfer in porous media using the mixed hybrid finite elements and the random-walk methods［J］.Mathematical Geology，2002，34：435-456.

［19］ELDER J W.The dispersion of marked fluid in turbulent shear flow［J］.Journal of Fluid Mechanics，1959，5（4）：544.

［20］NEPF H，GHISALBERTI M.Flow and transport in channels with submerged vegetation［J］.Acta Geophysica，2008，56（3）：753-777.

［21］FOLLETT E，HAYS C G，NEPF H.Canopy-mediated hydrodynamics contributes to greater allelic richness in seeds produced higher in meadows of the coastal eelgrass zostera marina［J］.Frontiers in Marine Science，2019，6：8.

［22］GHISALBERTI M，NEPF H M.The limited growth of vegetated shear layers［J］.Water Resources Research，2004，40（7）：1-12.

［23］MURPHY E，GHISALBERTI M，NEPF H.Model and laboratory study of dispersion in flows with submerged vegetation［J］.Water Resources Research，2007，43（5）：1-12.

［24］SANKARASUBRAMANIAN R，GILL W N.Unsteady convective diffusion with interphase mass transfer［J］.Proceedings of the Royal Society of London：A：Mathematical and Physical Sciences，1973，333（1592）：115-132.

［25］WANG Y F，HUAI W X.Random walk particle tracking simulation on scalar diffusion with irreversible first-order absorption boundaries［J］.Environmental Science and Pollution Research，2019，26（32）：33621-33630.

［26］BARTON N G.An asymptotic theory for dispersion of reactive contaminants in parallel flow［J］.The Journal of the Australian Mathematical Society，Series B：Applied Mathematics，1984，25（3）：287-310.

Effects of submerged vegetation and bed absorption boundary on pollutant transport in wetland

The study is financially supported by the National Natural Science Foundation of China（No.52020105006;No.51879199）.

FANG Haoze，YANG Zhonghua

（State Key Laboratory of Water Resources and Hydropower Engineering Science，Wuhan University，Wuhan 430072，China）

Abstract：Wetland is an important part of the ecosystem，and the investigation of wetland pollutant migration under the combined effect of submerged vegetation and bed absorption boundary can provide a reference for wetland design and maintenance.The random displacement model based on the Lagrangian method is adopted to simulate the transport process of instantaneously released pollutants in wetlands with dense rigid submerged vegetation and bed absorption boundary by setting different vegetation densities and bed absorption probabilities for the pollutants.Results indicate that the increase of the bed absorption probability accelerates the average migration velocity of the pollutant particle cloud and weakens its longitudinal dispersion，while the increase of vegetation density inhibits the bed absorption，extending the stay and greatly dispersing the distribution of the pollutants in the wetland，thereby giving full play to the comprehensive purification function of the wetland.When the absorption probability exceeds 10%，the absorption boundary of the bed can be regarded as a completely absorptive boundary.Conseqently，the use of a substrate with high absorption probability in wetland design is unnecessary.

Key words：pollutants transport;wetland;random displacement model;absorption boundary;submerged vegetation