变化环境下海河流域天然河川径流丰枯概率演变规律
2023-08-17鲁帆江明蒋云钟周毓彦徐扬
鲁帆 江明 蒋云钟 周毓彦 徐扬

摘要:海河流域天然河川径流持续衰减,水文丰枯情势显著变化,亟需研究适用于非一致性水文序列的丰枯概率计算方法。基于标准化径流指数、GAMLSS模型等方法,提出一种不同等级丰枯水事件期望发生次数和期望等待时间的计算方法,研究变化环境下海河流域天然河川径流丰枯概率的演变规律。结果表明:① 径流丰枯概率呈现出显著的枯增丰减趋势;② 同传统的一致性分布等多类概率分布相比,以时间t为协变量的LOGNO分布拟合流域径流系列的效果最优,且基于该分布计算的期望发生次数更接近于历史实际;③ 非一致性最优模型不同情景条件下计算的流域极端枯水和极端丰水事件的期望等待时间分别为4.9~9.4 a、14.5~36.0 a,说明海河流域近期发生极端枯水的概率远大于极端丰水。
关键词:河川径流;丰枯概率;非一致性;GAMLSS模型;海河流域
中图分类号:P333.1
文献标志码:A
文章编号:1001-6791(2023)01-0012-09
收稿日期:2022-09-08;
网络出版日期:2023-02-01
网络出版地址:https:∥kns.cnki.net/kcms/detail∥32.1309.P.20230131.1539.006.html
基金项目:国家重点研發计划资助项目(2021YFC3000200;2018YFC0406500)
作者简介:鲁帆(1981—),男,湖北天门人,正高级工程师,主要从事水文水资源研究。E-mail:lufan@iwhr.com
通信作者:江明,E-mail:1541427645@qq.com
河川径流对气候、下垫面等环境变化的响应敏感[1-2],部分流域由于环境变化破坏了径流序列的一致性,基于传统一致性假设的水文频率分析方法已不再适用[3-4],分析径流丰枯变化趋势与成因、深入研究环境变化对极值丰枯水事件时间间隔和发生概率的影响,对于流域水资源安全保障具有重要的实际意义。
已有研究常基于距平百分率、Z指数、标准化指数、概率矩阵等方法计算丰枯变化阈值和评价等级[5-7]。传统水文频率分析则采用矩法、三点法、权函数、极大似然等方法估计分布参数,计算水文极值的发生概率和重现期。当变量总体分布不便确定时,可采用核密度估计或基于径流形成因子推求分布概率[8]。许多研究考虑环境变化影响,引入时间、降水等协变量,构建变参数概率分布模型分析水文频率[9-11],其中GAMLSS(Generalized Additive Model for Location,Scale and Shape)模型研究较多[12-13]。非一致性条件下水文系列服从的分布参数每年不再是常量,国内外学者提出利用期望超过次数、期望等待时间、设计水平年限和等可靠度等方法推求变参数下指定设计标准(如百年一遇)的水文设计值[14-16],但上述方法的推演计算存在不确定性,应考虑水文序列的变化趋势和驱动机制,例如期望等待时间法在收敛前的预估时间越长,不确定性将越大[17-18] 。
近年来,海河流域径流呈现出显著的衰减趋势,对比2001—2021年与1956—2000年2个时期,流域后一时期多年平均降水量比前一时期减幅为1.9%,天然河川径流量减幅高达31.8%,已有研究认为社会经济取用水增加、下垫面变化、地下水超采等人类活动是径流减少的主要原因[19-20],洪水与径流的设计值均发生了较大变化[9]。
本文提出一套揭示变化环境下径流丰枯概率演变规律的计算方法,分析非一致性条件下海河流域天然河川径流丰枯变化及极值丰枯水事件发生次数、发生时间间隔的演变特征,并比较不同情景的计算结果,以期为未来水资源评价和旱涝风险管理提供科学依据。
1 研究区概况
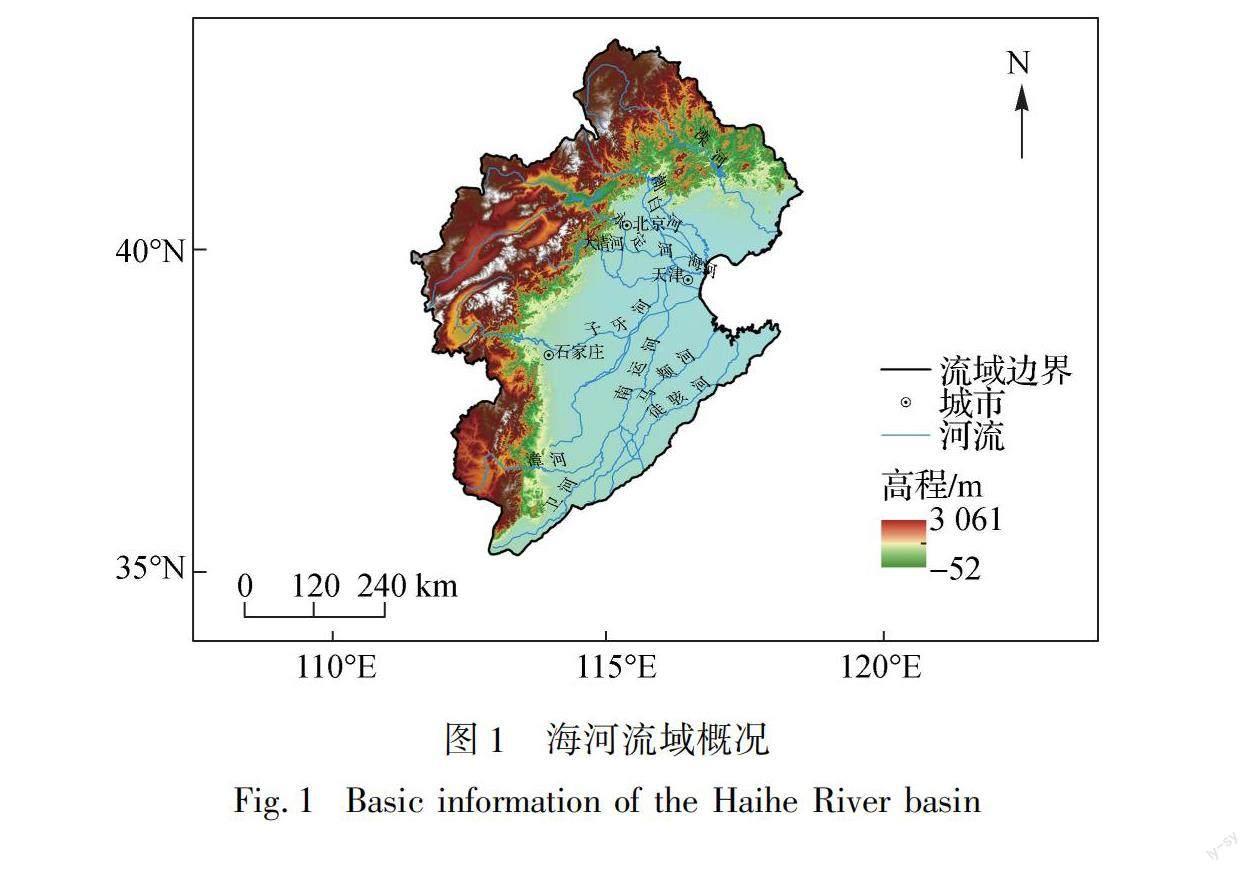
海河流域位于112°E—120°E、35°N—43°N之间,总面积约32万km2,包括滦河水系、海河北系、海河南系和徒骇马颊河水系4个水资源二级区,见图1。流域西部为山西高原和太行山区,北部为内蒙古高原和燕山山区,东部和东南部为广阔平原,山地和高原约占流域总面积的60%。流域属于温带半湿润、半干旱大陆性季风气候区,年平均气温为1.5~14 ℃,气温自西北向东南递增,年均气温差距较大,1961年来以每10 a超过0.30 ℃的速率显著上升,升温速率在中国仅次于青藏高原。1956—2021年多年平均年降水量为531.6 mm,年内分配极不均匀,夏季降水量占全年的60%~80%。流域河川径流变化剧烈,水土资源分布严重不匹配,本地水资源极度匮乏。多年来,通过开展生态清洁小流域建设、风沙源治理、坡耕地治理、退耕还林等工程,流域水土流失综合治理成效显著,林草覆盖率持续增加。遥感监测结果表明:1980—2020年间,海河流域山区耕地面积减少4 360 km2,林地面积增加840 km2,城镇居民用地增加5 450 km2。在多元因素共同作用下,山区植被生长状况明显改善,年均归一化植被指数(NDVI)由2000年的0.36增加到2020年的0.43(土地利用数据来源于中国科学院地理科学与资源研究所资源环境科学与数据中心,https:∥www.resdc.cn;NDVI数据来自美国NASA的MODIS产品数据MOD13A3v006,https:∥lpdaac.usgs.gov/products/mod13a3v006/)。
2 研究方法
M-K趋势检验和Pettitt突变检验法广泛应用于水文气象序列的统计检验[21]。本文首先基于上述方法分析海河流域降水及天然河川径流的变化趋势,利用标准化径流指数(SRI)划分径流丰枯,然后针对径流持续衰减的特征,通过GAMLSS模型确定径流系列的最优时变参数分布,得到最优分布下不同等级丰枯水事件的时变概率,在此基础上结合期望发生次数和期望等待时间法揭示非一致性条件下不同等级丰枯事件发生次数及极值丰枯水发生时间间隔的变化规律。
2.1 基于GAMLSS的丰枯概率计算
SRI是监测和评估水文干旱的一种指标,反映径流丰枯的变化程度。该指数通过对某个时间段的径流系列选取合适的概率分布,估计分布最优参数,采用等概率转换将径流量对应的累积概率进行正态标准化,从而得到一定时间尺度范围的SRI值。本文以SRI作为海河流域天然河川径流量的丰枯表征指标,其计算类似于表征气象干旱指标的标准化降水指数(SPI)[6],选用与SPI相同的等级划分标准,将径流丰枯划分为7个等级,详见表1。用ZSRI=y(y=-2,-1.5,-1,1,1.5,2)分别表示发生极端枯水、严重枯水、中等枯水、中等丰水、较大丰水和极端丰水的临界径流阈值。
GAMLSS模型包含众多分布函数,同时可灵活建立分布参数与时间、气象等协变量之间的函数关系[22-23] 。假设水文样本序列yt (t=1,2,…,n)服从分布函数Fz(yt|θt),其中θt=(θt1,θt2,θt3,…,θtp)是包含p个参数的向量,通常在建模中p≤4。用gk表示参数向量θt与解释变量Xk和随机效应项之间的单调连接函数,在实际建模过程中,通常忽略随机效应的影响,GAMLSS模型可表示为
式中:ηk和θt是长度为n的参数向量;βk为长度为Jk的回归参数向量;
Xk为n×Jk的解释变量矩阵;hjk为解释变量的函数,模型原理介绍可参考文献[23]。
采用AIC(Akaike Information Criterion)准则优选分布,值最小时对应的模型最优,同时借助残差正态QQ图和蠕虫图[24]评价模型拟合优度。基于最优GAMLSS分布模型,结合不同丰枯等级对应的临界径流阈值,可推导出非一致性条件下第t年不同等级丰枯水事件累积时变概率,见式(2)。
式中:ZSRI为丰枯等级阈值;θt为第t年的分布参数;pt为径流低于阈值ZSRI的累积时变概率。
2.2 期望发生次数
期望发生次数定义为从某一年开始在T年内某一等级丰枯水事件发生次数的期望值。记N(N=1,2,3,…,T)為在T年间出现某一等级以上丰枯水事件的可能次数。对于枯水事件,N=∑Tt=1I(Zt≤ZSRI),其中I(·)为示性函数,Zt为第t年的径流量。一致性条件下,随机变量N服从二项分布,记q0为径流低于某一等级枯水事件阈值的概率,则在T年内对应等级枯水事件的期望发生次数为Tq0。非一致性条件下,各等级水文事件在每年的发生概率不再为常数,此时N不再服从二项分布,在T年内某一等级以上枯水事件的期望发生次数为
式中:P(·)为发生括号内丰枯事件的概率。
对于丰水事件,记q1为一致性条件下径流高于某一等级丰水事件阈值的发生概率,则在T年内该等级以上丰水事件的期望发生次数为Tq1,非一致性条件下对应的期望发生次数为
2.3 期望等待时间
记T为首次出现某一等级丰枯事件的年份(T=1,2,3…,∞),期望等待时间E(T)定义为从某一年开始直到下一次某一等级丰枯事件出现的平均时间间隔。对于某一等级以上枯水事件,一致性条件下随机变量T服从几何分布,期望等待时间为1/q0,非一致性条件下T的概率密度函数及对应的期望等待时间分别为:
对于某一等级以上丰水事件,一致性条件下的期望等待时间为1/q1,非一致性条件下对应的期望等待时间为
3 结果与分析
3.1 径流变化趋势
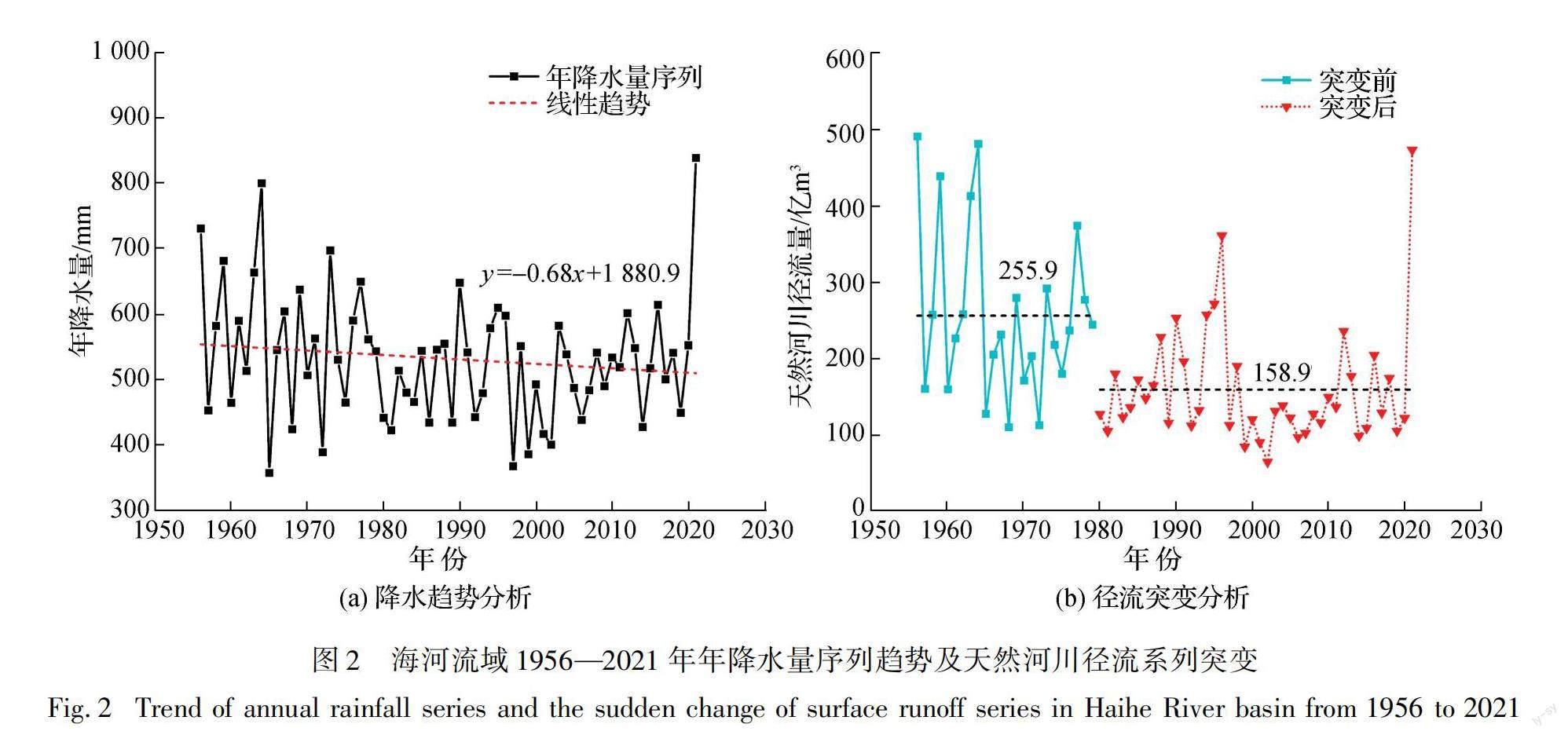
本文采用的海河流域1956—2021年降水及径流数据序列来源于第二次全国水资源调查评价和历年的《中国水资源公报》,趋势分析结果见图2。结果表明,流域年降水量存在轻微的下降趋势,M-K检验及Pettitt检验的p值分别为0.29和0.26,均未通过显著性水平95%检验,可认为该序列仍保持平稳性,而天然河川径流量下降趋势明显,M-K检验统计量为-3.58,通过了显著性水平为99%的趋势检验。Pettitt突变检验表明
,径流量向下跳跃突变发生于1979年,通过了显著性为95%的突变检验,1956—1979年多年平均天然河川径流量为255.9亿m3,1980—2021年则变为158.9亿m3,衰减幅度达38%。
3.2 概率计算模型优选
选取GAMLSS模型中6种常用的两参数分布为备选概率分布集,包括正态分布(Normal,NO)、对数正态分布(Log Normal,LOGNO)、耿贝尔分布(Gumbel,GU)、伽玛分布(Gamma,GA)、威布尔分布(Weibull,WEI)和逻辑斯谛分布(Logistic,LO),分布参数设置为常变量和以时间t为协变量,对流域天然河川径流量序列进行频率计算。为避免分布参数与时间t的回归方程太过复杂,分布位置参数和尺度参数与时间t的多项式次数不超过2,分别设为常变量及与时间t成1次方、2次方的多项式函数共9种组合对序列进行拟合,选取AIC值最小的概率分布和参数作为最优模型。结果表明,LOGNO分布的位置参数μ(t)=1 310-1.3t+0.000 32t2,尺度参数为常数时的模型AIC值最小,位置参数反映整个水文序列均值情况,体现了海河流域2010年前径流量持续减小、2010年后略有回升的趋势,与实际情况吻合。
为进一步验证最优非一致时变参数模型的拟合效果,防止模型过度拟合,图3展示了最优模型残差的正态QQ图和蠕虫图。QQ图上的散点分布在1∶1直线附近,认为最优模型的残差序列服从标准正态分布。蠕虫图中间的红线是由图中散点系列拟合的三次多项式曲线,所有散点都位于上下2条曲线之间的置信区间内,从而判断最优模型的分布类型和参数选择合理,模型拟合效果较好。
3.3 发生次数的比较
计算海河流域逐年SRI值(ISR),同时根据前面的径流量突变点分析结果,划分1956—1979年(简称PⅠ时期)及1980—2021年(简称PⅡ时期)2个时期揭示径流丰枯变化特征,ISR年际变化及不同时期丰枯等级发生次数见图4。结果表明:ISR呈显著的下降趋势(M-K检验统计量-3.6),通过置信水平95%的显著性检验,下降速率为0.34/(10 a),均值由PⅠ时期的0.84下降至PⅡ的-0.70。PⅠ时期丰水事件出现次数较多,而PⅡ时期丰水事件次数远低于枯水事件,枯水事件主要集中于1997—2010年间,甚至在2000—2001年连续出现极枯事件,河川径流的丰枯概率呈现出显著的枯增丰减趋势。Ling等[25]采用标准化降水蒸散指数(SPEI)研究海河流域气象干旱变化特征,结论与上述SRI有同样的变化规律,但SRI表征河川径流干枯程度更为嚴重。1964年和2021年分别是PⅠ、PⅡ时期降水量最大的年份,前者降水量相比后者少4.6%,但径流量却高出1.7%,可见流域内产流能力减弱,人类活动导致下垫面变化是河川径流减少的重要影响因素,同时气温升高、人类活动取用水、地下水超采等均有一定影响[19] 。
利用优选的LOGNO时变分布,计算不同等级丰枯事件在非一致性条件下的发生概率,采用期望发生次数法计算一致性和非一致性条件下海河流域历史期丰枯事件的期望发生次数,并与实际发生次数比较。由表2可知,一致性假设情况下,不同等级丰水和枯水事件的发生次数在PⅠ时期分别被低估和高估,而在PⅡ时期则分别被高估和低估。与一致性假设相比,考虑非一致性计算丰枯事件的期望发生次数与历史期的实际发生次数更接近,比较符合海河流域径流演变特征。因此,非一致性模型描述海河流域历史期丰枯特征要优于一致性模型。
3.4 极值丰枯事件的期望等待时间
探求未来极值丰枯事件发生的期望等待时间,重点是给出未来t=1 a,2 a,3 a,…的分布参数。鉴于径流变化存在一定的不确定性,本文立足于流域现状,基于3.2节拟合的最优时变LOGNO分布模型设置2种情景:一是假设未来年份维持非一致性模型的2021年分布(记为M1分布),此情景代表流域径流变化近期已接近稳定,分布参数及逐年发生极值丰枯事件的概率为固定值;二是以时间t为协变量往后延伸计算(记为M2分布),此情景下分布位置参数与时间t呈二次方,近期将呈现一定的增大趋势,代表流域在近期降水回升和水源涵养加强背景下未来径流将呈现一定的回升趋势。选取历史序列的下一年(2022年)作为起始年,计算不同分布下未来极端丰枯事件在第t年首次发生的概率及期望等待时间,如图5所示。
图5(a)和图5(b)纵坐标分别为极端丰水、极端枯水事件在未来第t年首次发生的概率。在M1分布下极丰事件的纵坐标随着t增大而减小,M2分布下极丰事件的纵坐标则先增加后减少,而极枯事件纵坐标均随着t增大而减小,但两者衰减速率有差异。图5(c)和图5(d)纵坐标分别为预估极端丰水、极端枯水事件的期望等待时间,M1、M2分布下极端丰水事件的期望等待时间分别为36.0 a、14.5 a,而在过去65 a中平均9.2 a出现一次极端丰水;在M1、M2分布下极端枯水事件的期望等待时间分别为9.4 a、4.9 a,而在过去65 a中平均21.6 a出现一次极端枯水,极枯事件的平均间隔时间将大幅缩短。本文中不同等级丰枯水事件期望等待时间的计算均能在未来15~30 a内收敛,模型预测的不确定性相对较小。综合上述分析,预估海河流域近期发生枯水的频率较高,发生丰水的频率相对较小,预估极枯、极丰事件下一次发生的期望等待时间分别为4.9~9.4 a和14.5~36.0 a。目前已有文献普遍认为下垫面与人类活动影响是海河流域径流减少的主要原因[19-20],由于这种影响带有一定的不可逆性,径流丰枯很难在短期内恢复到20世纪80年代以前的水平,因此,本文关于期望等待时间的计算结果与已有文献的认识相符。此外,由于不同气候变化排放情景和模式的预估结果间可能存在较大差异,本文在分析径流丰枯概率变化时没有考虑未来气候变化情景。
4 结论
本文针对海河流域径流量变化剧烈、水量锐减等问题,提出了一套研究变化环境下径流丰枯特征的计算方法,基于1956—2021年流域降水及天然河川径流量数据,研究了天然河川径流丰枯概率及未来发生时间间隔的演变规律,主要结论如下:
(1) 基于GAMLSS的时变矩模型中,以时间t为协变量的LOGNO分布为拟合径流系列的最优分布,且位置参数表征水文系列均值存在显著的非一致性,与时间t成二次多项式,尺度参数为常数。
(2) 流域标准化径流指数持续减小,径流丰枯概率呈现出显著的枯增丰减趋势。
(3) 非一致性条件下不同丰枯水等级在PⅠ与PⅡ 2个时期的期望发生次数更接近于实际发生情况,对于丰枯水事件拟合结果非一致性情况优于一致性假设情况。
(4) 预估极枯、极丰水文事件下一次发生的期望等待时间分别为4.9~9.4 a、14.5~36.0 a,发生枯水的频率相对较高,存在一定的不确定性。
参考文献:
[1]王国庆,张建云,管晓祥,等.中国主要江河径流变化成因定量分析[J].水科学进展,2020,31(3):313-323.(WANG G Q,ZHANG J Y,GUAN X X,et al.Quantifying attribution of runoff change for major rivers in China[J].Advances in Water Science,2020,31(3):313-323.(in Chinese))
[2]周祖昊,刘佳嘉,严子奇,等.黄河流域天然河川径流量演变归因分析[J].水科学进展,2022,33(1):27-37.(ZHOU Z H,LIU J J,YAN Z Q,et al.Attribution analysis of the natural runoff evolution in the Yellow River basin[J].Advances in Water Science,2022,33(1):27-37.(in Chinese))
[3]SUN P,WEN Q Z,ZHANG Q,et al.Nonstationarity-based evaluation of flood frequency and flood risk in the Huai River basin,China[J].Journal of Hydrology,2018,567:393-404.
[4]梁忠民,胡義明,王军.非一致性水文频率分析的研究进展[J].水科学进展,2011,22(6):864-871.(LIANG Z M,HU Y M,WANG J.Advances in hydrological frequency analysis of non-stationary time series[J].Advances in Water Science,2011,22(6):864-871.(in Chinese))
[5]白君瑞,徐宗学,班春广,等.基于Z指数的雅鲁藏布江流域径流丰枯变化及其特征分析[J].北京师范大学学报(自然科学版),2019,55(6):715-723.(BAI J R,XU Z X,BAN C G,et al.Runoff variation and characteristics in Yarlung Zangbo River by Z-index[J].Journal of Beijing Normal University(Natural Science),2019,55(6):715-723.(in Chinese))
[6]气象干旱等级:GB/T 20481—2017[S].北京:中国标准出版社,2017.(Grades of meteorological drought:GB/T 20481—2017[S].Beijing:Standards Press of China,2017.(in Chinese))
[7]涂新军,谢育廷,吴海鸥,等.基于概率矩阵的干旱等级变化评估及应用[J].水科学进展,2021,32(4):520-533.(TU X J,XIE Y T,WU H O,et al.An evaluation method for drought level changes based on probability matrix and its application[J].Advances in Water Science,2021,32(4):520-533.(in Chinese))
[8]熊立华,邝韵琪,于坤霞,等.年径流频率分析的一次二阶矩法及其应用[J].水科学进展,2017,28(3):390-397.(XIONG L H,KUANG Y Q,YU K X,et al.Derived moment approach for analyzing the annual runoff frequency and its application[J].Advances in Water Science,2017,28(3):390-397.(in Chinese))
[9]SONG X Y,LU F,WANG H,et al.Penalized maximum likelihood estimators for the nonstationary Pearson type 3 distribution[J].Journal of Hydrology,2018,567:579-589.
[10]LU F,SONG X Y,XIAO W H,et al.Detecting the impact of climate and reservoirs on extreme floods using nonstationary frequency models[J].Stochastic Environmental Research and Risk Assessment,2020,34(1):169-182.
[11]XIONG B,XIONG L H,GUO S L,et al.Nonstationary frequency analysis of censored data:a case study of the floods in the Yangtze River from 1470 to 2017[J].Water Resources Research,2020,56(8):e2020WR027112.
[12]顧西辉,张强,孔冬冬,等.新疆塔里木河流域洪水发生率非平稳性特征及气候变化影响研究[J].自然资源学报,2016,31(9):1499-1513.(GU X H,ZHANG Q,KONG D D,et al.Nonstationarity of flooding processes in the Tarim River basin and climate-related impacts[J].Journal of Natural Resources,2016,31(9):1499-1513.(in Chinese))
[13]XU Y R,LU F,ZHOU Y Y,et al.Dryness-wetness encounter probabilities analysis for lake ecological water replenishment considering non-stationarity effects[J].Frontiers in Environmental Science,2022,10:806794.
[14]YAN L,XIONG L H,GUO S L,et al.Comparison of four nonstationary hydrologic design methods for changing environment[J].Journal of Hydrology,2017,551:132-150.
[15]王银堂,李伶杰,胡庆芳,等.考虑局部趋势的非一致性水文频率分析方法[J].水科学进展,2017,28(3):406-414.(WANG Y T,LI L J,HU Q F,et al.Nonstationary hydrologic frequency analysis method considering local trends[J].Advances in Water Science,2017,28(3):406-414.(in Chinese))
[16]梁忠民,胡义明,王军,等.基于等可靠度法的变化环境下工程水文设计值估计方法[J].水科学进展,2017,28(3):398-405.(LIANG Z M,HU Y M,WANG J,et al.Estimation of design flood using equivalent reliability method under changing environment[J].Advances in Water Science,2017,28(3):398-405.(in Chinese))
[17]DU T,XIONG L H,XU C Y,et al.Return period and risk analysis of nonstationary low-flow series under climate change[J].Journal of Hydrology,2015,527:234-250.
[18]READ L K,VOGEL R M.Reliability,return periods,and risk under nonstationarity[J].Water Resources Research,2015,51(8):6381-6398.
[19]鲍振鑫,张建云,严小林,等.基于四元驱动的海河流域河川径流变化归因定量识别[J].水科学进展,2021,32(2):171-181.(BAO Z X,ZHANG J Y,YAN X L,et al.Quantitative assessment of the attribution of runoff change caused by four factors in the Haihe River basin[J].Advances in Water Science,2021,32(2):171-181.(in Chinese))
[20]YANG L,ZHAO G J,TIAN P,et al.Runoff changes in the major river basins of China and their responses to potential driving forces[J].Journal of Hydrology,2022,607:127536.
[21]WANG M H,JIANG S H,REN L L,et al.Nonstationary flood and low flow frequency analysis in the upper reaches of Huaihe River basin,China,using climatic variables and reservoir index as covariates[J].Journal of Hydrology,2022,612:128266.
[22]JEHANZAIB M,ALI SHAH S,YOO J,et al.Investigating the impacts of climate change and human activities on hydrological drought using non-stationary approaches[J].Journal of Hydrology,2020,588:125052.
[23]RIGBY R A,STASINOPOULOS D M.Generalized additive models for location,scale and shape (with discussion)[J].Journal of the Royal Statistical Society:Series C (Applied Statistics),2005,54(3):507-554.
[24]魯帆,肖伟华,戴雁宇,等.黄河干流年径流量非一致性频率计算[J].水力发电学报,2020,39(12):76-84.(LU F,XIAO W H,DAI Y Y,et al.Study on non-stationary frequency calculations for the annual runoff of Yellow River mainstream[J].Journal of Hydroelectric Engineering,2020,39(12):76-84.(in Chinese))
[25]LING M H,GUO X M,SHI X L,et al.Temporal and spatial evolution of drought in Haihe River basin from 1960 to 2020[J].Ecological Indicators,2022,138:108809.
Evolution law of wet and dry probability of natural river runoff in Haihe River basin under changing environment
The study is financially supported by the National Key R&D Program of China(No.2021YFC3000200;No.2018YFC0406500).
LU Fan1,JIANG Ming1,JIANG Yunzhong1,ZHOU Yuyan1,XU Yang1,2
(1. Department of Water Resources,China Institute of Water Resources and Hydropower Research,Beijing 100038,China;2. School of Resources and Earth Science,China University of Mining and Technology,Xuzhou 221116,China)
Abstract:The natural river flow in the Haihe River basin has been continuously reducing in recent years,which leads to significant changes particularly in the wet and dry conditions of hydrology.As such,research on the calculation method of wet and dry probability catering for nonstationary hydrological series is needed.Based on the standardized runoff index and GAMLSS model,a new method computing expected number of occurrences (ENO) and expected waiting time (EWT) was proposed according to different levels of wet and dry hydrological events.Then,we further investigate on the evolution law of probability of wet and dry of natural river flow in Haihe River basin under changing environment.Our main finding are outlined as follows:① The probability of wet and dry of surface runoff showed a significant trend of increasing low flow and decreasing high flow.② Compared with other probability distributions including the traditional stationary hypothesis,the LOGNO distribution with time(t) as the covariate has the best performance when fitting the surface runoff series.The ENO of wet and dry hydrological events in the historical period calculated based on this distribution is closer to the actual situation.③ The EWT of extremely dry and wet hydrological events in the Haihe River basin calculated under different scenarios of the nonstationary optimal model were 4.9—9.4 a and 14.5—36.0 a respectively,indicating that the considerably higher likelihood of extreme dry event in oncoming future.
Key words:river runoff;wet and dry probability;nonstationary;GAMLSS model;Haihe River basin
