考虑风场影响的城市建筑区产流计算方法
2023-08-17高希超王浩杨志勇高凯牟亚莉
高希超 王浩 杨志勇 高凯 牟亚莉


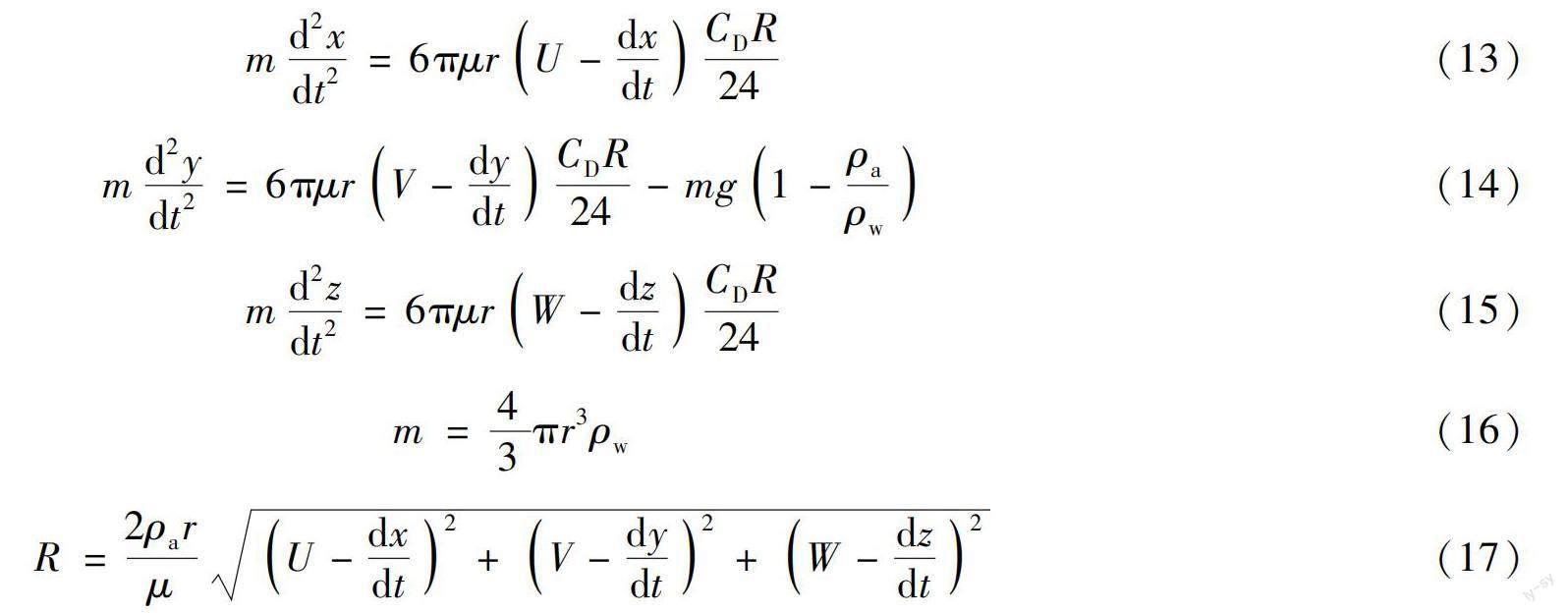
摘要:风场作用下城市建筑物的遮挡作用直接影响区域产流过程,为提高城市雨洪模拟精度,需揭示风场作用下建筑区的独特产流机理并构建相应的计算方法。将建筑区的产流面划分为水平面和竖直面,基于计算流体力学理论求解降雨倾角,结合几何关系确定降雨在水平面和竖直面上的分布,通过产流理论分别计算2类产流面的产流,提出建筑区的产流计算方法,并将其耦合入SWMM模型在试验流域进行了验证。结果表明:① 改动模型所模拟的径流的纳什效率系数整体高于原始SWMM模型,且洪峰模拟效果更好;② 改动模型的土壤饱和导水率等关键参数取值更为合理;③ 改动模型对不同气象条件下建筑区产流模拟的稳定性更好。该方法可提高建筑区产流模拟精度。
关键词:产流;城市建筑区;倾斜降雨;风场
中图分类号:TV11
文献标志码:A
文章编号:1001-6791(2023)01-0088-14
收稿日期:2022-06-28;
网络出版日期:2022-11-21
网络出版地址:https:∥kns.cnki.net/kcms/detail/32.1309.P.20221118.1731.002.html
基金项目:国家自然科学基金资助项目(51879274;52209044)
作者简介:高希超(1988—),男,山東滨洲人,博士,主要从事城市水文方面研究。E-mail:999gaoxichao@163.com
通信作者:杨志勇,E-mail:yangzy@iwhr.com
受气候变化与城镇化影响,中国城市洪涝防治形势日益严峻[1-4]。明晰城市流域的产汇流机理、准确预测城市流域的产汇流过程是认识并解决城市洪涝问题的关键[5-8]。相较于自然流域,建筑区是影响城市区域降水产汇流的重要因素,且其面积占整个城市建成区面积的比例超过63.7%(《中国城市建设统计年鉴:2020》),因此,厘清建筑区的产汇流机理是准确模拟城市区域产汇流过程的必要条件。风场作用下雨滴运动轨迹会发生倾斜,倾斜降雨被建筑物遮挡导致部分原应作用于地表的降雨作用于建筑物侧壁;加之建筑物侧壁的渗透能力一般远小于地表的渗透能力,建筑物侧壁的产流会经由散水、截水沟等装置直接进入地下管网等快速排水系统,导致建筑区产流特点发生改变。此外,前人研究表明中国主要城市存在明显的风雨同期现象[9],上述风场造成的建筑区的独特产流现象不可忽视。Gao等[10]和Yoo等[11]通过实验室物理模型试验和数值模拟试验证实了风场对建筑区的产流过程具有显著的影响。
然而,当前大多数的城市水文模型在计算建筑区产流时将建筑区概化为一个平面,通过不透水面占比情况来考虑建筑物对降雨产流的影响[12-13],此类方法不能描述风雨遭遇情况下建筑物壁面的产流过程。虽然在模型应用时可通过调整不透水率等参数来获取较满意的结果,但其存在以下问题:① 建筑物遮挡对区域产汇流的影响随风速、风向的变化而变化,通过不透水率等静态参数无法考虑此动态过程,导致模型的预测能力存在不确定性;② 建筑群中建筑物的几何构成和空间分布存在异质性,导致建筑物的遮挡作用可能存在区域差异。因此,尽管2个子汇水区具有相同的集水面积和水文参数,产汇流过程却可能呈现出各异的变化特征,而现有模型的产流计算模式无法区分这一差异。
为解决上述当前城市水文模拟中存在的问题,本文在深入剖析城市建筑区下垫面特点的基础上,揭示城市建筑区的产流机理,提出城市建筑区的产流计算方法,并应用该方法对SWMM模型的产流模块进行改进,旨在为城市建筑区的水文模拟提供更为准确的模拟方法。
1 城市建筑区产流计算方法
1.1 倾斜降雨条件下建筑区产流计算方法
城市建筑区的产流特点如图1所示。由于建筑物的遮挡作用,发生倾斜降雨时,原本作用于建筑物背风侧地表(图1中大括号所示区域)的降雨改为作用于建筑物侧壁,导致城市建筑区的产流表现为建筑物侧壁、建筑物屋面和地表组合产流的特点;根据《建筑与小区雨水控制及利用工程技术规范:GB50400—2016》,建筑物侧壁的径流系数显著大于地面(渗透铺装)的径流系数(表1),而且建筑物侧壁产生的径流一般会经由建筑物周边的散水直接进入地下排水管网等快排系统(图1);以上因素叠加,导致有风情况下建筑区径流系数较无风情况下增加。此外,一般情况下风场和降雨是非恒定的,导致降雨的倾斜程度呈现出时变的特征。降雨倾斜程度的变化会导致雨水在建筑物侧壁和地表的分配比例发生变化,进而改变建筑区的产流特点,导致城市建筑区的径流系数呈现出明显的时变特征。
基于上述机理分析,本文以图2所示简化城市建筑区为例,推导了考虑风场影响的城市建筑区的产流计算公式。图中,h为建筑物高度;θ为降雨倾角;b和l分别为建筑物的宽度和长度;B和L分别为整个建筑区的宽度和长度;φ为风速方向与建筑物长边法线方向的夹角简称为风向角,φ∈0,π/2;A为任意面积;r为受风场干扰前雨强;rinc为受风场干扰后倾斜降雨的雨强;rh为倾斜降雨雨强的水平向分量;rw为倾斜降雨雨强的竖直向分量(地面监测站所测量到的雨强),以上各类雨强的单位均为m/s。受不均匀风场的影响,城市建筑区落地雨的雨强分布不均,为便于计算,在推导中上述雨强皆采用其作用范围内的平均雨强。在倾斜降雨的作用下,建筑区的产流可分为由竖直向降雨分量驱动的水平面产流和由水平向降雨分量驱动的竖直面产流2部分。
建筑区水平面产流包括建筑物屋面产流和地表产流,其产流量可表示为
式中:Qw为水平面产流流量,m3/s;f和froof分别为地表渗透速率和屋面渗透速率,m/s;n为建筑区中建筑物的个数(图2中n=1);bcosφ+lsinφ为建筑物在与风速垂直方向上的等效宽度,m。式(1)中右端第1项为单位时间内作用于地表和建筑物屋面的降水量總和,右端第2项为单位时间内地表的渗透水量,右端第3项为单位时间内屋面的渗透水量。
建筑区竖直面产流主要是建筑物侧壁的产流,其产流量可表示为
式中:Qh为竖直面产流流量,m3/s;fwall为竖直面渗透速率,m/s。
将式(1)和式(2)相加即可获得整个建筑区的产流流量(Q):
将式(4)带入式(3)可得:
1.2 降雨倾角计算
降雨倾角是公式(5)中唯一的未知量,本节介绍如何对降雨倾角进行求解。求解降雨倾角需获取风场中雨滴的运动轨迹。目前求解风场中雨滴运动轨迹的常规方法是基于欧拉-拉格朗日观点的计算流体力学(CFD)方法。该方法假设建筑物周边的风场为恒定场,首先基于欧拉的观点采用雷诺时均方程对风场进行模拟,然后采用拉格朗日的观点将雨滴视为球形粒子,通过运动方程来求解雨滴在风场中的运动轨迹。根据雨滴运动轨迹与建筑物及地表的相交情况即可求得降雨的倾斜角度。
1.2.1 基于CFD方法的降雨倾角计算
(1) 建筑区风场模拟。建筑物周围的风场通过连续方程、雷诺时均方程和标准k-ε湍流方程进行模拟,其数学表达式如下:
式中:Ui、Uj分别为i、j(i=1,2,3;j=1,2,3)方向的平均风速;xi、xj分别为i、j方向的位置;ui、uj分别为i、j方向的紊动风速;P为压强;ρ为空气密度;-uiuj为雷诺切应力;k为紊动能;ε为紊动能耗散系数;vt为紊流涡黏性;ν为运动黏性;δij为Kronecker算子;Cμ、Cε1、Cε2、σk和σε为量纲一参数,取值一般如下:
(2) 风场中雨滴运动轨迹模拟及降雨倾角计算。雨滴在风场中受重力和风场施加的拖拽力控制,其运动状态可通过运动方程求解,具体如下:
式中:r为雨滴等效半径;ρa、ρw分别为空气和水的密度;μ 为空气黏性;U、V、W 分别为x、y、z方向的风速;m为雨滴质量;R为雨滴相对于风场运动的雷诺数;CD为风场施加于雨滴的拖拽力系数。
雨滴运动轨迹与建筑物和地面相交点之间的平均割线倾角即为降雨倾角,求得雨滴的运动轨迹之后便可通过三角函数关系获取降雨倾角。
1.2.2 降雨倾角计算算例
受建筑物扰动影响,不同建筑区的风场分布可能存在明显差异,进而导致其降雨倾角不同。本文以GAO等[10]设计的城市建筑区产汇流试验平台为例来说明应用上述方法来进行降雨倾角计算的具体流程。
该试验平台由人工降雨系统、送风系统、建筑区比尺物理模型等部分构成。试验平台参照某典型小区按照1∶100的比例构建,平台上按照500 mm的间隔依次放置3栋建筑物模型,每栋建筑物模型的尺寸(长×宽×高)为700 mm×250 mm×1 000 mm,试验平台各组成部分的详细介绍参见文献[10]。
由于试验平台为对称结构,为节约计算时间,本文以试验平台的对称面为基准,建立了针对试验平台的二维CFD模型(图3)。为减小出口边界对模拟结果的影响,选择背风侧距离建筑物模型为15h的平面作为计算域的出口。其他边界按照试验平台的具体情况确定,具体为:风速测量装置所在的平面作为计算域的风速入口边界,试验大厅顶板(降雨喷头)所在的平面作为计算域的上边界,试验平台的底部平台上层(建筑物底层)所在的平面作为计算域的下边界。计算域的上下边界和建筑物表面采用无滑移边界,靠近壁面处流场采用标准壁面函数处理。入口边界处采用速度入口边界条件,受送风装置的尺寸影响,入口处的风速剖面表现为分段特征,其表达式如式(18)所示,入口处的紊流边界由紊动能及紊动能耗散率表示。出口边界处采用自由出流边界条件。降雨由从计算域顶部释放球形惰性粒子进行模拟,粒子直径相同,粒子数沿着释放平面呈均匀分布,释放范围为从风速入口边界到建筑物模型背风侧5h处。另外,在应用运动方程计算粒子的运动轨迹时不考虑粒子的扩散情况。
式中:U0为面平均风速;UL为入口边界处的风速。
采用Fluent对上述二维CFD模型进行求解。由图3可知,所选实例计算区域比较规则,因此可采用结构化网格来对其进行离散。经网格无关性检验,最终确定采用尺寸为15 mm×15 mm的矩形网格对计算域进行离散。另外,由于壁面处的气流情况比较复杂,为准确获取近壁处的风场特点,对靠近建筑物壁面处的网格进行了加密处理。离散后计算域共包含1 012 469个网格,采用二阶迎风格式对控制方程进行离散,采用压力耦合方程组的半隐式方法(the Semi-Implicit Method for Pressure Linked Equations,SIMPLE)对离散后的控制方程进行迭代求解。另外,本文所模拟的工况属于恒定问题,因此未设置模型的具体模拟时长,当各相关变量前后时段的残差稳定且达到终止条件时即可结束模拟(一般在2 000次循环内即可达到稳定),此时模型输出的结果即为最终结果。
应用上述CFD模型,本文共进行了6种入口风速(0、1.8、2.5、4.0、4.9、5.9 m/s)和6种雨滴粒径(1.5、1.8、2.0、2.5、2.8、5.0 mm)组合工况下的模拟试验共36组,模拟结果如图4所示。结果表明,降雨倾角随雨滴粒径的增加而减小,随风速的增加而增加。为探究建筑区风场分布及雨滴运动轨迹情况,随机选取任一工况下的风速分布及雨滴运动轨迹如图5所示。结果表明,建筑扰动导致其上空出现风速加强带,风场使雨滴运动轨迹发生倾斜。
1.3 降雨倾角简化算法
上述通过CFD方法求解雨滴运动轨迹进而求解降雨倾角的方法比较复杂,难以在城市雨洪模型中耦合应用。然而,由图5可以看出,在相同建筑物分布条件下,不同粒径雨滴的运动轨迹与风速近似呈幂函数关系,因此,可通过CFD方法的模拟结果来建立降雨倾角与风速和雨滴粒径之间的统计关系以便于将其应用于水文模型。假设tanθ与风速及雨滴粒径的关系如下:
式中:d为雨滴直径,mm;a为尺度参数,受建筑物几何尺寸影响;b、c为形状参数,受建筑物几何尺寸及雨滴粒径影响。
经由最小二乘法拟合后式(19)的计算结果与算例1.2中CFD模型模拟结果的对比情况如图4所示。结果表明式(19)所示函数形式可以较好地表达降雨倾角与风速及雨滴粒径之间的统计关系。另外,建筑物对风场的干扰主要受迎风向第一栋较高建筑物控制,且不同建筑物分布对局部风场的影响规律类似。因此,可假设建筑物的分布情况不会对降雨倾角和风速的关系类型造成影响。即可采用式(19)来近似求解建筑区中风场导致的降雨倾角。
雨滴粒径为非常规气象变量,一般气象站点未对其进行监测,但有研究表明降雨强度与雨滴直径分布的中位数呈线性正比关系[14]。为方便应用,采用降雨强度替换式(19)中的雨滴直径:
式中:I为降雨强度,mm/h;α、β和γ为与建筑物的几何特征和雨滴粒径及其分布相关的参数,可采用相关优化算法或者手动试错方法,通过雨强、风速、径流等要素对耦合后的水文模型率定反演获得。
2 应用验证
为验证上述建筑区产流计算方法,采用广州市天河智慧城试验流域相关实测数据,借助SWMM模型的基本框架,分别基于本文所提的产流计算方法和SWMM模型原有产流计算方法模拟试验区降水产流过程,并通过对比评估二者的模拟效果检验本文提出的计算方法。
2.1 流域概况
天河智慧城坐落于广州市天河区的东北部(113°23′52″E、23°10′12″N),属于亚热带季风性气候,年降水量为1 620~1 680 mm,变差系数为0.211,多年平均年降水量为1 650 mm,年内降水分布十分不均,整体呈现夏季、秋季降水多,春季、冬季降水少的特点,4—9月降水量占全年降水量80.3%,極端降雨事件较多,易导致洪涝灾害。天河智慧城地势平坦,海拔由北向南逐渐减小,建设用地占整个研究区域的69%,主要土地利用类型为商业、服务业设施。
本试验流域位于天河智慧城南侧,总面积为11.37 ha2。研究区域西南部的智慧城管委会办公楼楼顶装有自记式雨量计,精度为0.2 mm,用于测量研究区域内的降水。研究区域排水系统出口附近的检修孔装有超声波流量计,精度为2% FS,采集间隔为1 min,用以测量出口流量。以上测量设备全部由THWater公司(http:∥www.thuenv.com/)提供。研究区域及监测设备布置如图6(地图来源: Google,Maxar Technologies)所示。
本文选取2018年5月至2019年9月共8场降雨数据及其对应的排水系统出口的流量数据对建筑区产流计算方法进行验证。降雨数据具体情况如表2所示。所选降雨数据中,最大降水量为61.4 mm,最大降雨历时为350 min,最小降水量为8.4 mm,最小降雨历时为17 min。由于缺少风速实时监测数据,本文采用降雨当日试验区所在区域(天河区)的日均风速(https:∥hz.hjhj-e.com/home)作为改动模型的风速输入数据。
2.2 模型结构
改动模型采用了SWMM模型的基本框架,但对其产流模块进行了调整。SWMM模型将城区下垫面分为3类,分别是透水面、有调蓄能力的不透水面和无调蓄能力的不透水面,因此,模型仅模拟了降水在上述3种下垫面类型上的产汇流过程,忽略了风场作用下建筑物侧壁对降水产汇流过程的影响。本文所述改进模型在原有3类产流面上新增加建筑物侧壁产流面。在原始SWMM模型中,Tsubcatch结构体中的成员变量SubArea[3]对应于上述3种产流面;本模型将该变量修改为SubArea[4],并在Tsubarea结构体中新增成员变量,例如n、b、l、 φ等描述建筑物形状和尺寸的参数(式(2)),以及α、β、γ等描述侧壁产流过程的参数(式(20))。基于上述改动,本研究在SWMM模型产流计算函数getSubareaRunoff中新增侧壁产流计算模块,以模拟降水作用于建筑物侧壁不透水面后的产流过程。实现这一计算过程的具体流程如下:① 应用式(4)和式(20)计算水平向降
水分量,确定发生在建筑物侧壁的雨量;② 应用式(2)计算建筑物侧壁产流面的产流量;③ 根据建立的建筑物位置与管网拓扑关系,为建筑物侧壁产流量分配对应的入流管网。此外,风场作用下建筑物的遮挡作用将减少部分地表产流面的接收的降水量,本研究进一步根据式(1)修正地表产流面的面积,然后根据修正后的面积采用原模型计算方法确定地表产流量。
2.3 模型构建
分别应用原始SWMM模型以及基于本文提出的建筑区产流计算方法的SWMM模型对上述试验流域的8场次降雨径流过程进行了模拟。除与降雨倾角相关的3个参数外,原始模型与改动模型参数一致,基于前人研究成果,本文选取了不透水区和透水区的曼宁系数、不透水区和透水区的地表填洼量以及流域坡度、特征宽度、土壤饱和导水率和土壤缺水量等8个参数作为率定参数。由于所选试验流域面积较小,模型参数的空间分布对模拟结果影响较小,除特征宽度,本文对流域内不同产流单元采用相同的参数值。特征宽度是影响产流单元汇流特性的重要参数,为考虑不同产流单元的汇流特性且不增加模型率定的复杂度,本文采用式(21)建立产流单元特征宽度与其面积的关系,通过率定参数K对城市的所有产流单元的特征宽度进行率定。不透水区面积占比通过实地调研获得,不作为率定参数,建成区值为0.7,未建成区为0.1。各参数详情见表3。
式中:W为产流单元特征宽度;AS为产流单元面积;K为产流单元特征宽度与面积的相关系数。
采用可考虑参数不确定的DREAM方法分别对2个模型进行率定,前6场实测降雨径流用于率定模型,后2场实测降雨径流用于验证模型,模型率定的目标函数为径流时间序列的水量误差和径流峰值的水量误差,模型模拟效果用Nash-Sutcliffe效率系数(ENS)来进行评估。
2.4 模拟结果
取DREAM算法中各马尔可夫链满足稳定条件的3 000组参数作为模型的最终可接受参数,其分布如图7所示。除土壤饱和导水率外,2个模型的参数分布情况基本一致。SWMM模型的土壤饱和导水率显著小于改动模型的土壤饱和导水率且其分布集中于先验区间的左侧,表明在SWMM模型中该参数并没有达到合理的取值。相较而言,改动模型的土壤饱和导水率的后验概率分布更接近于正态分布,表明改动模型可以获得该参数的合理取值,且其取值与曾家俊等[15]研究中该参数的调查取值基本一致。因此,可以认为改动模型能够更好地反映流域内土壤渗透的实际情况。SWMM模型渗透参数偏低的原因可能是模型不考虑风对建筑区产流的增大效用,通过调整渗透参数来平衡模拟和实测之间的水量差,导致参数失真。
将全部可接受参数带入模型并取95%置信区间后可获得改动模型与原始SWMM模型考虑不确定性的径流模拟结果如图8和图9所示。结果表明,2个模型都能够较好地模拟流域的径流过程,但是除20180530号观测试验外,原始SWMM模型对洪峰有较明显的低估现象,改动模型对洪峰的模拟效果明显优于原始SWMM模型。但是,部分场次 (如20180828、20180831)模拟径流量低于实测过程。对比分析可知,径流低估多发生于18:00—22:00,此时为居民生活污水排放高峰期,生活污水对实测径流过程扰动较大。模型结构并未考虑社会水循环,从而导致了这一模拟偏差。此外,SWMM模型的结构存在一定缺陷,未考虑建筑物侧壁产流,一定程度上低估了不透水面的占比,导致低估区域产流。目前大多数文献在应用SWMM模型时将不透水面占比也作为率定参数,掩盖了忽略侧壁产流导致的径流低估问题。但是,不透水面占比具有明确的物理意义,是可调查参数,不应作为率定参数参与模型率定。本文在率定SWMM模型时未对该参数进行率定,可能造成了对径流的低估。
本文对比了改动模型与原始SWMM模型在不同降雨观测试验中的模拟精度,采用ENS评估,详见表4和图10。结果表明除20180530号和20180724号观测试验外,改动模型模拟与实测径流间的ENS均高于原始SWMM模型。雖然改动模型关于20180530号和20180724号观测试验的ENS略微小于原始SWMM模型,但其中位数均大于0.88,表明改动模型能够很好地反映该次降雨的径流响应。另外从ENS的箱型图范围来看,改动模型模拟径流的不确定性也显著小于原始SWMM模型模拟径流的不确定性。
根据率定期和验证期的划分,本文进一步评估了改动模型与SWMM模型在各时期的模拟效果(图11),结果表明,率定期和验证期改动模型的ENS均高于原始SWMM模型。率定期原始SWMM模型的ENS的中位数为0.58,而改动模型的ENS的中位数为0.83;验证期原始SWMM模型的ENS的中位数为0.36,而改动模型的ENS的中位数为0.60。
3 结论
本文分析了建筑区的产流特点及其影响因素,揭示了风场对建筑区产流的影响,将风场作用下城市建筑区产流划分为地表产流、建筑物屋面产流和建筑物侧壁产流,提出了考虑风场作用的城市建筑区产流计算方法,并结合SWMM模型在广州市天河智慧城试验流域进行了应用验证,结论如下:
(1) 理论分析表明,风场导致的倾斜降雨作用于建筑物侧壁并发生产流可改变城市建筑区的产流特点,风速、风向和雨滴粒径是影响城市建筑区产流的重要因素。
(2) 通过对模型结构进行优化,改动模型中关键参数(如土壤饱和导水率)的分布较原始SWMM模型要更为合理。
(3) 以纳什效率系数作为评估标准,改动模型在试验流域取得了较好的应用,整体模拟精度和对洪峰的模拟效果均显著高于原始SWMM模型。
参考文献:
[1]徐宗学,程涛.城市水管理与海绵城市建设之理论基础:城市水文学研究进展[J].水利学报,2019,50(1):53-61.(XU Z X,CHENG T.Basic theory for urban water management and sponge city:review on urban hydrology[J].Journal of Hydraulic Engineering,2019,50(1):53-61.(in Chinese))
[2]张建云,王银堂,贺瑞敏,等.中国城市洪涝问题及成因分析[J].水科学进展,2016,27(4):485-491.(ZHANG J Y,WANG Y T,HE R M,et al.Discussion on the urban flood and waterlogging and causes analysis in China[J].Advances in Water Science,2016,27(4):485-491.(in Chinese))
[3]宋晓猛,张建云,贺瑞敏,等.北京城市洪涝问题与成因分析[J].水科学进展,2019,30(2):153-165.(SONG X M,ZHANG J Y,HE R M,et al.Urban flood and waterlogging and causes analysis in Beijing[J].Advances in Water Science,2019,30(2):153-165.(in Chinese))
[4]王小杰,夏军强,董柏良,等.基于汇水区分级划分的城市洪涝模拟[J].水科学进展,2022,33(2):196-207.(WANG X J,XIA J Q,DONG B L,et al.Simulation of urban flood using the SWMM with the hierarchical catchment partition method[J].Advances in Water Science,2022,33(2):196-207.(in Chinese))
[5]张红萍,李敏,贺瑞敏,等.城市洪涝模拟应用场景及相应技术策略[J].水科学进展,2022,33(3):452-461.(ZHANG H P,LI M,HE R M,et al.Application scenarios and corresponding technical strategies of urban flood modeling[J].Advances in Water Science,2022,33(3):452-461.(in Chinese))
[6]周宏,刘俊,高成,等.考虑有效不透水下垫面的城市雨洪模拟模型:Ⅰ:模型原理与模型构建[J].水科学进展,2022,33(3):474-484.(ZHOU H,LIU J,GAO C,et al.Development of an urban stormwater model considering effective impervious surface:Ⅰ:theory and development of model[J].Advances in Water Science,2022,33(3):474-484.(in Chinese))
[7]周宏,刘俊,高成,等.考虑有效不透水下垫面的城市雨洪模拟模型:Ⅱ:雨洪模拟及水文响应分析[J].水科学进展,2022,33(3):485-494.(ZHOU H,LIU J,GAO C,et al.Development of an urban stormwater model considering effective impervious surface:Ⅱ:urban stormwater simulation and anaysis of hydrological response[J].Advances in Water Science,2022,33(3):485-494.(in Chinese))
[8]梅超,刘家宏,王浩,等.城市下垫面空间特征对地表产汇流过程的影响研究综述[J].水科学进展,2021,32(5):791-800.(MEI C,LIU J H,WANG H,et al.Comprehensive review on the impact of spatial features of urban underlying surface on runoff processes[J].Advances in Water Science,2021,32(5):791-800.(in Chinese))
[9]MARTIUS O,PFAHL S,CHEVALIER C.A global quantification of compound precipitation and wind extremes[J].Geophysical Research Letters,2016,43(14):7709-7717.
[10]GAO X C,YANG Z Y,HAN D W,et al.The impact of wind on the rainfall—runoff relationship in urban high-rise building areas[J].Hydrology and Earth System Sciences,2021,25(11):6023-6039.
[11]YOO C,CHO E,NA W,et al.Change of rainfall—runoff processes in urban areas due to high-rise buildings[J].Journal of Hydrology,2021,597:126155.
[12]李美水,杨晓华.基于Sobol方法的SWMM模型参数全局敏感性分析[J].中国给水排水,2020,36(17):95-102.(LI M S,YANG X H.Global sensitivity analysis of SWMM parameters based on Sobol method[J].China Water & Wastewater,2020,36(17):95-102.(in Chinese))
[13]SYTSMA A,CROMPTON O,PANOS C,et al.Quantifying the uncertainty created by non-transferable model calibrations across climate and land cover scenarios:a case study with SWMM[J].Water Resources Research,2022,58(2):e2021WR031603.
[14]LAWS J O,PARSONS D A.The relation of raindrop-size to intensity[J].Transactions,American Geophysical Union,1943,24(2):452.
[15]曾家俊,麥叶鹏,李志威,等.广州天河智慧城SWMM参数敏感性分析[J].水资源保护,2020,36(3):15-21.(ZENG J J,MAI Y P,LI Z W,et al.Sensitivity analysis of SWMM parameters in Guangzhou Tianhe wisdom city[J].Water Resources Protection,2020,36(3):15-21.(in Chinese))
Runoff calculation method of urban built-up areas considering the impact of wind
The study is financially supported by the National Natural Science Foundation of China(No.51879274;No.52209044).
GAO Xichao1,2,WANG Hao1,2,YANG Zhiyong1,2,GAO Kai1,2,MOU Yali1,2
(1. State Key Laboratory of Simulation and Regulation of Water Cycle in River Basin,Beijing 100038,China; 2. China Institute of Water Resources and Hydropower Research,Beijing 100038,China)
Abstract:The shielding effect of urban buildings under the action of wind field directly affects the process of precipitation runoff.To improve the accuracy of urban stormwater simulation,it is necessary to uncover the unique runoff characteristics of built-up areas under the action of wind field and establish corresponding calculation methods.The runoff surface of built-up areas was divided into horizontal and vertical runoff surfaces,and the rainfall inclination angle caused by the wind field was calculated based on computational fluid dynamics theory.Geometric relationships were integrated to determine the distribution of inclined rainfall on the horizontal and vertical runoff surfaces.Based on the runoff theory,the runoff of the two types of runoff surfaces was calculated and formed the runoff calculation method of built-up areas.The method was coupled into the storm water management model (SWMM) and verified in the experimental watershed.The results showed that:① the modified SWMM had higher Nash model efficiency coefficient than the original SWMM,and simulated flood peak better;② the values of some key parameters,such as soil saturated conductivity,obtained via the modified model were more appropriate;③ the modified model was more stable for runoff simulation of built-up areas under different meteorological conditions.Therefore,this method can improve the simulation accuracy of runoff in built-up areas.
Key words:runoff;urban built-up areas;inclined rainfall;wind field
