利用卷积神经网络的土壤有机质含量高光谱估测

刘杰亚，李西灿，任文静，吴亚楠

(山东农业大学 信息科学与工程学院，山东 泰安 271018)

土壤有机质含有作物和微生物生长发育所需要的各种物质，准确估算土壤有机质含量是土壤养分诊断和实现农田精准管理的基础［1］。传统的土壤有机质测定方法成本高、操作复杂，难以满足现代农业的需求［2-3］。近年来，高光谱技术因其光谱分辨率高、波段范围广等优点在农业、林业、海洋等领域得到广泛应用［4-6］，成为土壤有机质含量估测的1 种新技术，具有广阔的应用前景。

运用高光谱技术估测土壤有机质含量，国内外学者已开展了较多的研究。目前，用于估测土壤有机质含量的方法主要有多元线性回归（MLR）、偏最小二乘回归（PLSR）、模糊识别、机器学习、灰色关联识别等。史舟等［7］结合土壤光谱分类和PLSR 的多变量校准，使土壤有机质的估测精度得到有效提高。官晓等［8］基于68 组土壤样本，对比MLR 和模糊数学2 种方法的估测精度，结果表明模糊数学周期短、成本低，估测精度高。包青岭等［9］基于灰色关联分析和随机森林构建估测模型，结果表明机器学习分类方法适用于特征波段的分类，且估测精度较高。李西灿等［10］结合有序的灰色累积生成和灰色GM（0，N）模型建立高光谱灰色估算模型，结果表明土壤有机质估测精度得到明显提高。苗传红等［11］提出基于灰色关联识别的估测模型及残差修正模型，并应用于土壤有机质光谱估测，取得了较好的效果。曹雪松等［12］将统计分析和灰色关联分析相结合，建立了土壤含水量高光谱灰色关联局部回归模型，该模型在土壤有机质高光谱估测中也取得较好效果。Sina Mallah Nowkandeh 等［13］基于乌罗米亚半干旱地区的样本数据，对比PLSR 等多种方法，结果表明，PLSR 的估测精度相对较高。Amanda SilveiraReis 等［14］基于巴西巴拉那州的384 个土壤样本，使用PLSR 建立模型，取得较好估测结果。Aghajani M 等［15］分别使用人工神经网络和多元线性回归建立土壤有机质估测模型，结果表明人工神经网络的整体估测效果优于多元线性回归，获得较小的估测误差。Panagiotis Tziachris 基于希腊地区的土壤样本数据，使用多种机器学习方法构建估测模型，结果表明，机器学习方法中随机森林和梯度提升方法具有较高的估测精度［16］。Bruno Pedro Lazzaretti 等［17］基于支持向量机建立土壤有机质含量估测模型，取得较好估测精度。

随着大数据、计算能力、新算法和数字计算工具的发展，深度学习算法已逐步用于对高光谱数据的特征进行分类和提取［18］，越来越多的研究者开始用深度学习的卷积神经网络（Convolutional Neural Network，CNN）解决土壤光谱估测的问题，且取得较好的研究成果［19］。J.Padarian 的研究表明CNN 模型能够从原始光谱数据中估测土壤特性，是土壤光谱数据建模的理想工具，且与传统方法相比，估测效果明显变好［20］。Wartini Ng 等［21］研究发现CNN 估测模型保留了与实测值类似的相关性，与传统方法相比，CNN 模型具有更高的性能。杨杰超等［22］基于大型土壤光谱库，建立了基于CNN 和循环神经网络的联合架构，结果表明CNN 和循环神经网络的架构具有出色的降噪和可转移能力，且估测能力相较于传统模型得到明显提高。

已有研究表明CNN 对于非线性数据具有较强的特征提取能力，且相较于传统的学习模型具有较好的模型表达能力和较高的拟合精度，并已应用于土壤养分的估测［23-24］，但CNN 的拟合精度高并不一定能同时保证模型的预测精度高。因此，本文基于山东省济南市章丘区的76 个土壤样本的原始光谱数据，首先采用主成分分析对光谱降维，并构造光谱信息矩阵；然后利用CNN 模型提取土壤有机质光谱信息特征，通过模型参数优化建立土壤有机质含量光谱CNN 估测模型；最终采用决定系数R2和平均相对误差（Mean Relative Error，MRE）检验模型估测精度。

1 研究区与数据获取

1.1 研究区概况

本研究采用山东省济南市章丘区的土壤数据。章丘区位于济南市的东部，地势包含山丘、丘陵、平原，南高北低，黄河流经北境。境内包含棕壤、褐土、水稻土、潮土等众多土壤种类，其中褐土占地面积最广，大多位于中南部地区，为境内主要土类。

1.2 土壤样品采集

在山东省济南市章丘区按照事先设定的路线采集深度为（0～5 cm）的表层土壤样本，采集时使样本均匀分布，并使用手持GPS 对采样点定位，之后将采集的土壤样本数据按编号放入密封袋，共采集76 个土壤样本。

1.3 光谱测量及有机质含量测定

使用美国ASD FieldSpecPro FR 光谱仪采集76个土壤样本的高光谱数据，采集时传感器与土样距离15 cm，3°视场角照射，得到波段范围为350 ～2 500 nm，间隔为1 nm 的数据，每个样本进行10 次测量，取平均值以减少误差。采用重铬酸钾—外加热法测定每个样本的有机质含量。

2 算法描述

2.1 主成分分析

在CNN 计算过程中，为避免出现维度灾难、内存计算量巨大、训练困难等问题，在保留数据特征信息的情况下，采用主成分分析（Principal Component Analysis，PCA）对光谱数据进行降维处理。PCA 是1 种用于简化高维数据复杂性同时保持其方差的工具［25］，该方法在原有数据特征基础上构造出来的新特征，所包含的信息与原数据特征所包含的信息基本一致［26］，避免了数据特征信息流失，一定程度上提高了模型的稳定性。

2.2 光谱信息矩阵生成

所有样本的光谱数据经PCA 方法降维后生成新的主成分数据向量，再利用该主成分数据向量按式（1）生成光谱信息矩阵。设S为某一样本的光谱数据经PCA 降维后的主成分数据向量，则变换后的光谱信息矩阵为：

式中，N为变换后的光谱信息矩阵。

对每个样本光谱的主成分数据向量进行变换生成光谱信息矩阵，不仅能够满足CNN 输入所需的数据结构要求，在统计学中这种变换还可以保留数据所有原始信息［27］，为后续构建四维光谱信息矩阵做铺垫。

2.3 卷积神经网络

近几年，随着机器学习的发展，CNN 已在越来越多的领域得到应用，例如目标检测、图像分类和光谱分析。CNN 主要由卷积层、池化层和完全连接层构成。卷积层通过稀疏局部连接和权值共享机制，可以从输入的特征映射中学习局部模式，减少模型的可训练参数，单个卷积层能够识别简单的特征，随着卷积层层数增加，网络可提取的特征越加复杂和抽象。通过池化层操作，减少冗余，降低计算成本并减少过拟合的风险。CNN 通过叠加多个卷积层和池化层来提取输入数据中局部和抽象的特征。最后，完全连接层由一些神经元组成，这些神经元用以整合从卷积层和池化层提取的所有特征以获得输出结果。常见的CNN 结构如图1 所示。

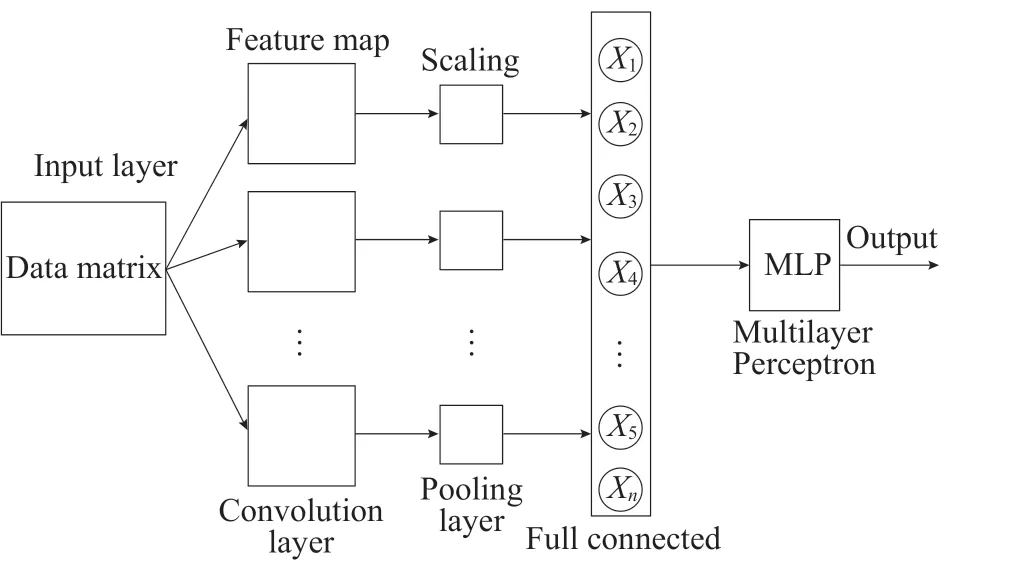
图1 CNN 结构Fig.1 CNN structure

3 数据处理与建模

3.1 光谱数据预处理

由于ASD FieldSpecPro FR 光谱仪在1 000 nm 附近采集光谱数据时会产生跳跃现象，因此在进行其他操作之前，需先使用光谱仪自带的View Spec Pro 软件修复光谱数据，校正断点。为减小噪声的影响，采用九点加权平均法对光谱曲线进行去噪预处理［28］。

在光谱数据采集时，由于受到周边环境、人为操作等客观因素的影响，会使某些光谱数据产生异常，影响估测精度，为防止异常样本的影响［29］，对比分析土壤有机质含量与光谱曲线的走势，按照有机质含量与光谱反射率呈负相关的规律，剔除1、2、19、29、32、60 号样本，剩余70 个样本用于建模和检验。

将剩余样本根据有机质含量从小到大的顺序排列，再按照有机质含量在9 ～16、16 ～19、19 ～23、23 ～30 g/kg 区间内分为4 组，取每组样本对应光谱反射率的平均值，得到4 组光谱反射率曲线如图2 所示。

图2 按土壤有机质含量分组的平均反射率Fig.2 Average reflectance of different soil organic matter content

光谱曲线除存在断点外，由于受大气水汽的强烈影响，在1 350 ～1 450 nm、1 800 ～1 900 nm波段产生剧烈波动，因此将其予以剔除。由图2 可见，随着土壤有机质含量升高土壤光谱反射率降低，此趋势与已有相关研究结论相符［30］。土壤光谱反射率整体呈上升的趋势，在波长2 200 ～2 500 nm之间呈下降趋势，其中光谱曲线3 个吸收峰分别在1 400、1 800、2 100 nm 附近。

3.2 光谱数据降维

为减少内存计算量和充分利用光谱特征信息，将光谱去噪后的数据使用SPSS14.0 软件确定累计方差贡献率到达99.99%时的主成分数目，即选择的主成分数目为34；利用Python 中sk-learn 库中的PCA 方法对原始光谱数据降维，并将提取的34 个主成分数据进行归一化处理。

3.3 四维光谱信息数组构建

将PCA 后的样本随机分为58 个建模样本和12个检验样本。为适应CNN 的输入结构要求，需要对利用PCA 提取的主成分数据向量进行矩阵变换，首先按式（1）将每个样本的主成分数据向量变换为二维光谱信息矩阵，再将建模样本变换为（58,1,34,34）的四维光谱矩阵，检验样本变换为（12,1,34,34）的四维光谱矩阵，其中每个光谱矩阵包含 1 个信息层，1 个34×34 的光谱信息矩阵，58、12 为样本数目。

3.4 模型设计

使用Python 语言并基于Tensorflow 框架搭建CNN 模型，网络模型具体结构如图3 所示。模型的输入是四维光谱矩阵和有机质含量的实测值，输出是土壤有机质含量的估测值。其中卷积层的卷积核大小为3×3，步长为1，数量为1，用于从输入数据中提取不同的局部特征，获取局部抽象特征映射；核权重采用随机初始化，偏置全零初始化，以RELU 作为卷积层的激活函数。池化层输入数据为卷积层的输出数据，采用平均池化方法，尺度为2×2，用于逐步减小卷积层生成的输出特征映射的空间大小。多元感知器神经元个数为256 层，输入数据为池化层数据，输出数据为估测值。

图3 CNN 估测模型结构Fig.3 CNN estimation model structure

建模模型采用AdamOptimizer 算法进行训练，目标函数是实测值与估测值之间损失平方之和，采用梯度下降算法计算目标函数最小值。为减小训练过程中权重、偏置变化带来的估测精度不稳定的影响，在每次迭代过程中分别计算建模样本的损失函数Loss值和检验样本的平均相对误差MRE，在最终的估测结果中选取检验样本MRE最小值所对应的建模样本的权重、偏置参数计算最终估测结果。

其中，建模样本损失函数Loss的计算公式为：

式中，y＾i是估测值，yi是实测值，n为建模样本数。

网络训练过程中的损失函数如图4 所示。由图4 可知，训练过程中随着迭代次数的增加，网络损失函数值逐渐减小，网络逐渐收敛。

图4 模型训练过程中的损失函数值Fig.4 Loss function value during model training

3.5 精度评价指标

本文采用决定系数R2和平均相对误差MRE检验模型的模拟和预测精度，计算公式为：

4 结果与分析

4.1 估测结果

为寻找最优模型结构，进行多种不同卷积层、不同卷积核的模型对比，最终得到包含1 个3×3 的卷积核，1 个平均池化层，1 个全连接层的模型，估测效果最优。为对比分析，将学习速率设为0.01，分别进行迭代次数为300、400、500、600、700、800 次的实验，结果见表1。检验样本的土壤有机质实测值和估测值的关系如图5 所示。

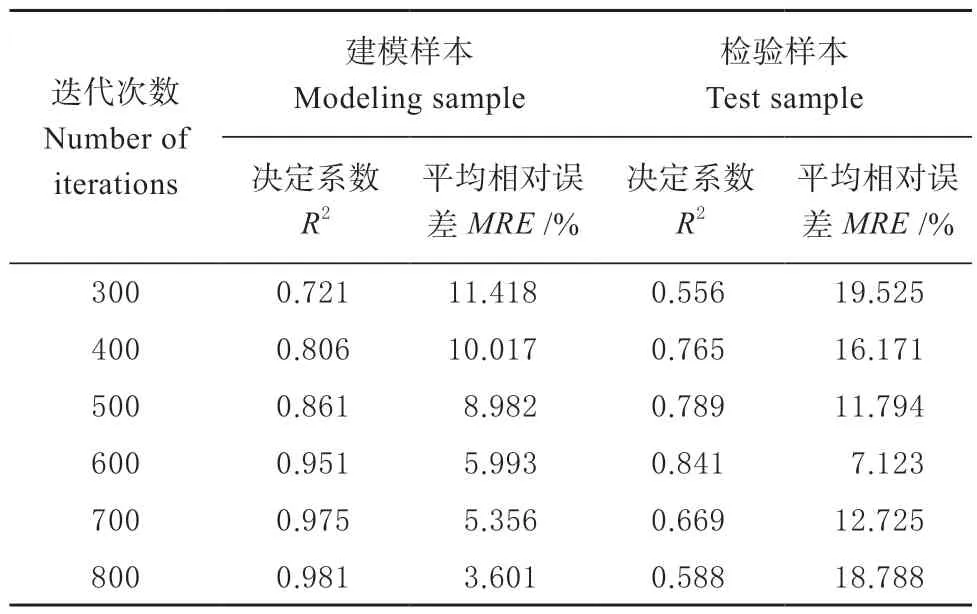
表1 不同迭代次数的精度对比表Table 1 Accuracy comparison table for different iteration times

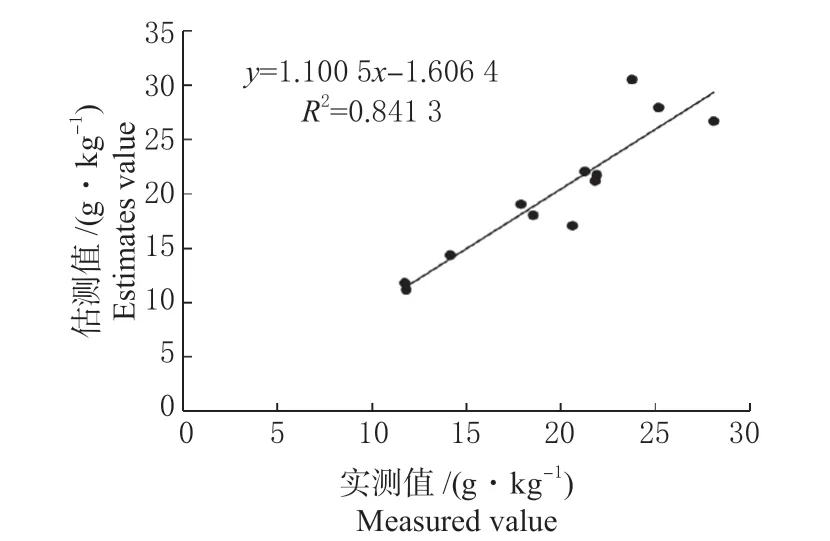
图5 CNN 模型估测结果Fig.5 CNN Mode Estimation Results

由表1 可见，当学习速率为0.01 时，随着迭代次数的增加，建模样本的决定系数R2逐渐增大、平均相对误差MRE逐渐减小；而检验样本的决定系数R2先逐渐增大后逐渐减小、平均相对误差MRE先逐渐减小后逐渐增大。当迭代次数为600 次时，检验样本的估测精度为最优，其中R2为0.841，MRE为7.123%。

4.2 对比分析

为进一步说明本文模型的有效性，再分别采用常用的多元线性回归(MLR)、BP 神经网络(BP)和支持向量机(SVM)进行建模。建模时，取主成分分析的前5 个主成分作为特征因子，如表2 所示。

表2 PCA 方差及累积贡献率Table 2 PCA variance and cumulative contribution rate

由表2 可见，前5 个主成分因子累计方差贡献率达99.884%。计算时，首先将这5 个特征因子进行归一化处理。BP 神经网络采用单隐层结构，隐含层节点数为5；支持向量机采用交叉验证和网格搜索法参数寻优，交叉验证折数为5，结果如表3 所示。

表3 不同模型精度对比Table 3 Accuracy comparison of different models

由表3 可知，CNN 模型的建模和估测精度均优于BP、SVM 和MLR；检验样本基于传统估测模型的R2均低于0.8，且MRE均大于10%，而CNN 模型的估测精度R2为0.841，MRE为7.123%，相较于传统模型有明显提高。

目前在土壤有机质含量估测领域的研究，大多数估测结果的R2介于0.67 ～0.77 之间［31-33］。相较而言，本文基于CNN 的土壤有机质含量估测精度较高。

CNN 估测模型相较于MLR、BP 神经网络、SVM 具有较好的拟合及估测能力，可以提取、学习光谱的特征信息，降低无关信息的干扰。另一方面，相较于传统的方法而言，基于PCA 的CNN 只需要将低维的光谱信息矩阵数据输入网络，简化了光谱数据，最大程度上保留了光谱特征信息，同时大幅降低了计算工作量，因此达到较好的估测效果。本研究表明基于CNN 的土壤有机质含量估测是可行有效的，可为实际工作提供借鉴。

5 结论

本文基于山东省济南市章丘区土壤样本的高光谱数据，采用基于CNN 的建模方法，实现了对土壤有机质含量的估测。结果表明，基于CNN 的估测模型对土壤有机质含量的估测是可行有效的，通过CNN 模型结构和参数优化，不仅能实现建模样本的高精度拟合，而且可得到检验样本的高精度估测，且估测精度明显优于传统模型，可为土壤有机质含量高光谱估测提供1 种新思路。但如何寻找最优网络参数，进一步提高估测精度等有待深入探究。