2D伺服阀二元缝隙流启动阻力及其影响因素
2023-08-17陆倩倩黄程威阮健
陆倩倩 ,黄程威 ,阮健
(1.浙大城市学院工程学院,浙江杭州 310015;2.上海交通大学机械与动力工程学院,上海 200030;3.浙江工业大学特种装备制造与先进加工技术教育部重点实验室,浙江杭州 310014)
0 前言
伺服阀作为伺服系统核心元件,其性能对系统起到至关重要的影响。二维(2D)伺服阀[1]因其高功率质量比、抗污染能力强等优点,被用于航空航天、军事等领域。2D伺服阀的阀芯在结构上属于滑阀阀芯,工作时,利用阀芯转动实现先导控制,同时阀芯的轴向移动实现功率放大,故称双自由度伺服阀。2D伺服阀阀芯与阀套(阀体)为面接触,运动时会产生泄漏和磨损,而且阀芯运动为双自由度,故泄漏和磨损表现出的特性与传统滑阀不同。陈大为[2]通过仿真和实验方法研究了传统液压滑阀泄漏、卡紧等与均压槽尺寸和分布之间有关系,明确合理布置均压槽能够减小阀芯卡紧力,过多的均压槽会增加滑阀泄漏。刘继凯等[3]通过仿真研究了温度和压力对电液比例多路阀泄漏特性的影响,明确增加配合长度、减小偏心对减小缝隙泄漏有益。巴鹏等人[4]运用CFD技术研究了截止阀启闭过程中的阻力特性,推导出阀口开度、流速、公称直径与压力损失之间的数学模型,简化了研究问题的难度。李双双等[5]运用计算流体力学证明了多路阀微沟槽摩擦特性优于传统均压槽,且可以有效提高高压多路阀使用寿命。GARCIA[6]提出一种简单的算法估算控制阀Karnopp摩擦模型,可以估算摩擦因数、运动部件的质量及弹簧刚度。HIDALGO、 GARCIA[7]通过非线性滑膜控制算法补偿并减小控制滑阀上摩擦损失。OKHOTNIKOV等[8]通过计算流体力学研究了转动流量阀的扭矩及压力损失。以上文献均针对传统滑阀运动时的摩擦阻力进行了结构和控制方面的研究。
一些学者针对缝隙流的影响因素进行了研究,贾晓萌等[9]通过仿真和实验确定了雷诺数的增大会增大管道缝隙流流速,且入口处的流速最大;高永华等[10]通过实验研究了缝隙流流量、直径与压降之间的关系;FENG等[11]通过实验研究了动过程中间隙区流场的建立过程和不同宽高比对间隙区流场的影响;HSU、 CHEN[12]通过仿真对正常和倾斜缝隙流进行研究,正常缝隙流在不同雷诺数下,阻力所受的影响因素是不同的,而倾斜缝隙流的阻力主要受缝隙流倾角的影响;孙蕾[13]通过实验研究了雷诺数与缝隙流的直径比对轴向流速的影响,确定了两者对轴向流速是相互影响的。
结合2D伺服阀的工作特点,其阀芯相对传统滑阀增加了转动的自由度,启动时的阻力是影响伺服阀特性的关键因素。目前在2D伺服阀阀芯上缝隙流引起摩擦损失方面的研究尚属空白,因此本文作者针对2D伺服阀阀芯双自由度的运动特点,通过理论和仿真手段研究阀芯和阀套之间二元缝隙流特点,以及对阀芯启动摩擦阻力及影响因素。
1 2D伺服阀结构和工作原理
2D伺服阀结构如图1所示,主要由阀体、阀芯、阀座和端盖组成,阀芯的中心有细长孔,将P口高压油通过槽a引入阀芯右侧b处和右侧的高压孔处;阀套左侧开有螺旋槽,高压油通过高压孔与螺旋槽形成的节流口1和低压孔与螺旋槽形成的节流口2流回T口。零位时,两节流口面积相同,根据液压半桥原理,螺旋槽内压力为高压油的一半,螺旋槽与阀芯左侧敏感腔相通,故敏感腔处压力是高压油一半;结构上,阀芯左侧受压面是阀芯右侧b处受压面的两倍,此时,阀芯轴向受力平衡,当阀芯逆时针旋转,高压孔处节流口面积增加,敏感腔压力上升,破坏了阀芯力平衡,阀芯右移,此时P口通B口,A口通T口,当右移至两先导级节流口面积再次相同时,阀芯停留在新的平衡位置上;当阀芯顺时针旋转时,情况相反。
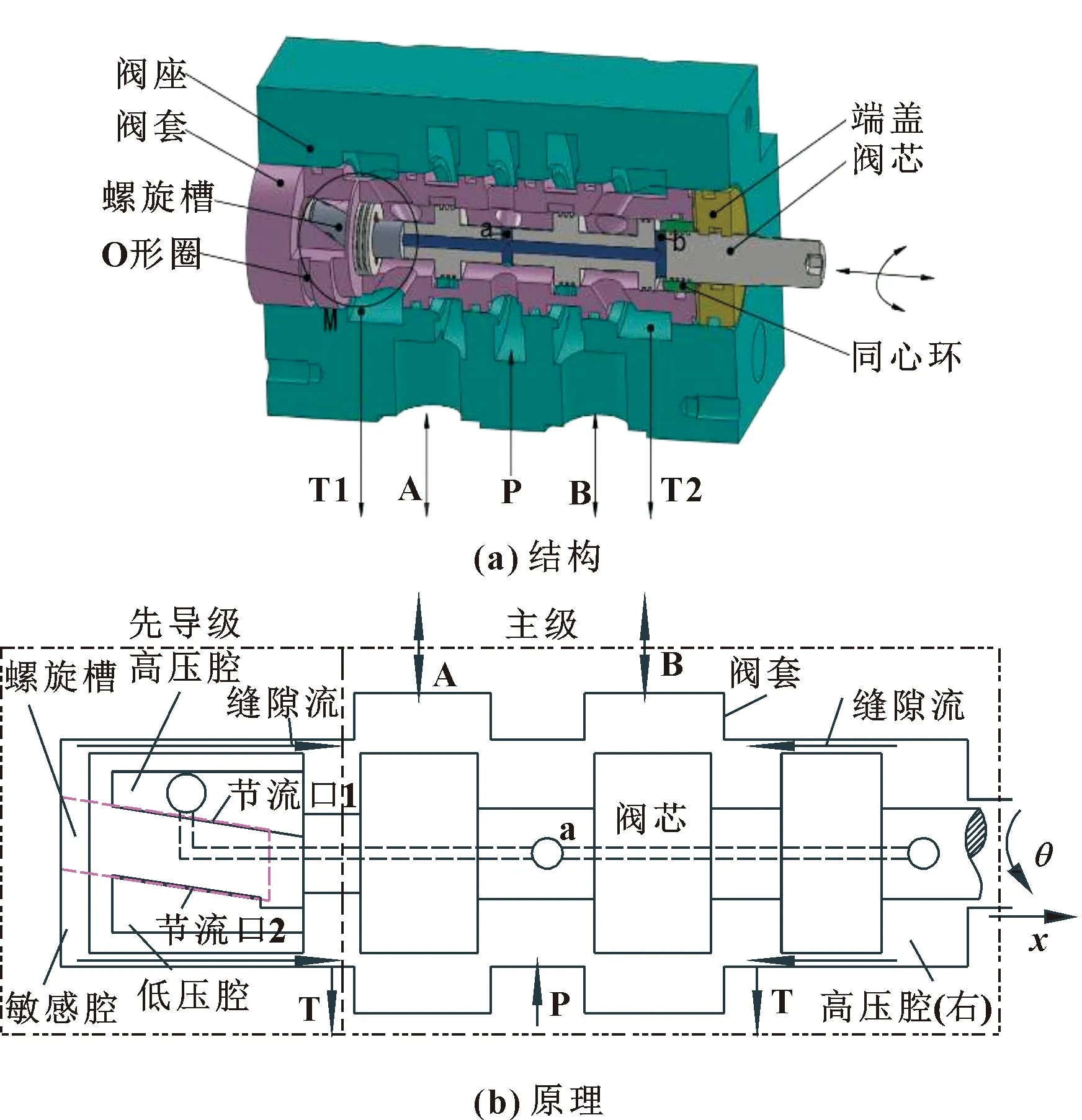
图1 2D伺服阀
根据2D伺服阀的工作原理可知,阀芯启动的过程为:首先,在电机械转换器的驱动下旋转;然后,在阀芯左右两腔压力差的作用下轴向运动;最后,由先导级螺旋槽和高低压腔形成的位置反馈,停止在特定的位置。因此,图1中阀芯的左侧凸肩和右侧凸肩在启动过程,由于旋转运动和台肩两侧压差,在阀芯(台肩)和阀套(或阀体)的缝隙中会产生二元缝隙流。
2 二元缝隙流理论分析
当2D伺服阀阀芯在电机械转换器驱动下旋转时,阀芯右侧凸肩及左侧先导级凸肩与阀体(阀套)形成的缝隙同时存在周向的剪力流和轴向的压力流的二元缝隙流,如图1(b)所示。将两侧缝隙流视为两平行平板间的二元缝隙流,其模型示意和流速分布示意如图2所示。图中:l表示平板的长度,m;s表示平板的宽度,m;δ表示两平板间的缝隙高度,m;p1、p2分别表示入口和出口的压力,MPa;uy0表示动平板在y方向的初始速度,m/s。

图2 二元缝隙流动速度分布示意
设流体在重力场作用下,质量力在坐标轴的3个方向的大小分别为:x=y=0,z=-g,则N-S方程为
(1)

(2)
(3)
考虑实际阀芯阀体运动特征,阀芯仅存在y方向的移动uy,x方向运动速度ux为0。同心情况下,y方向存在剪力流,x方向是压力流,故:
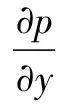
(4)
(5)
将式(4)和(5)代入式(2)和(3),结合压差缝隙流量公式,得:
(6)
(7)
双自由度滑阀副摩擦损失不可避免,且与传统单方向滑动滑阀的能量损失不同。
在x方向的剪切应力:
(8)
当z=δ时:
(9)
在y方向的剪切应力为
(10)
当z=δ时:
(11)
式(9)和(11)表示壁面z=δ处由压差和壁面运动引起的液体剪应力,且方向互相垂直。由此,运动壁面上的摩擦力Ff为
(12)
式中:取平面宽度s为πd,则公式(12)可视为圆环缝隙二元流动下壁面所受的摩擦力。取阀芯台肩直径d=22 mm;台肩宽l=12 mm,压差为5 MPa,黏度为0.027 9 Pa·s,内壁面的线速度分别为0.5、5、10 m/s时,由公式(12)计算二元缝隙流的摩擦力随缝隙宽度的变化关系如图3(a)所示。当阀芯台肩线速度为5 m/s,缝隙流入口和出口压差分别为1、5、10 MPa时,二元缝隙流的摩擦力随缝隙宽度变化的曲线如图3(b)所示。其结果与同条件下的一元流动(压差相同,动壁面的运动速度相同)对比可知:无论是不同壁面转速还是端面压差,二元缝隙流的最小摩擦力小于一元流动的;且缝隙相同时,二元流动的摩擦力偏小。由曲线变化规律知,随着缝隙宽度增加,两类缝隙流动对应的摩擦阻力趋于一致。
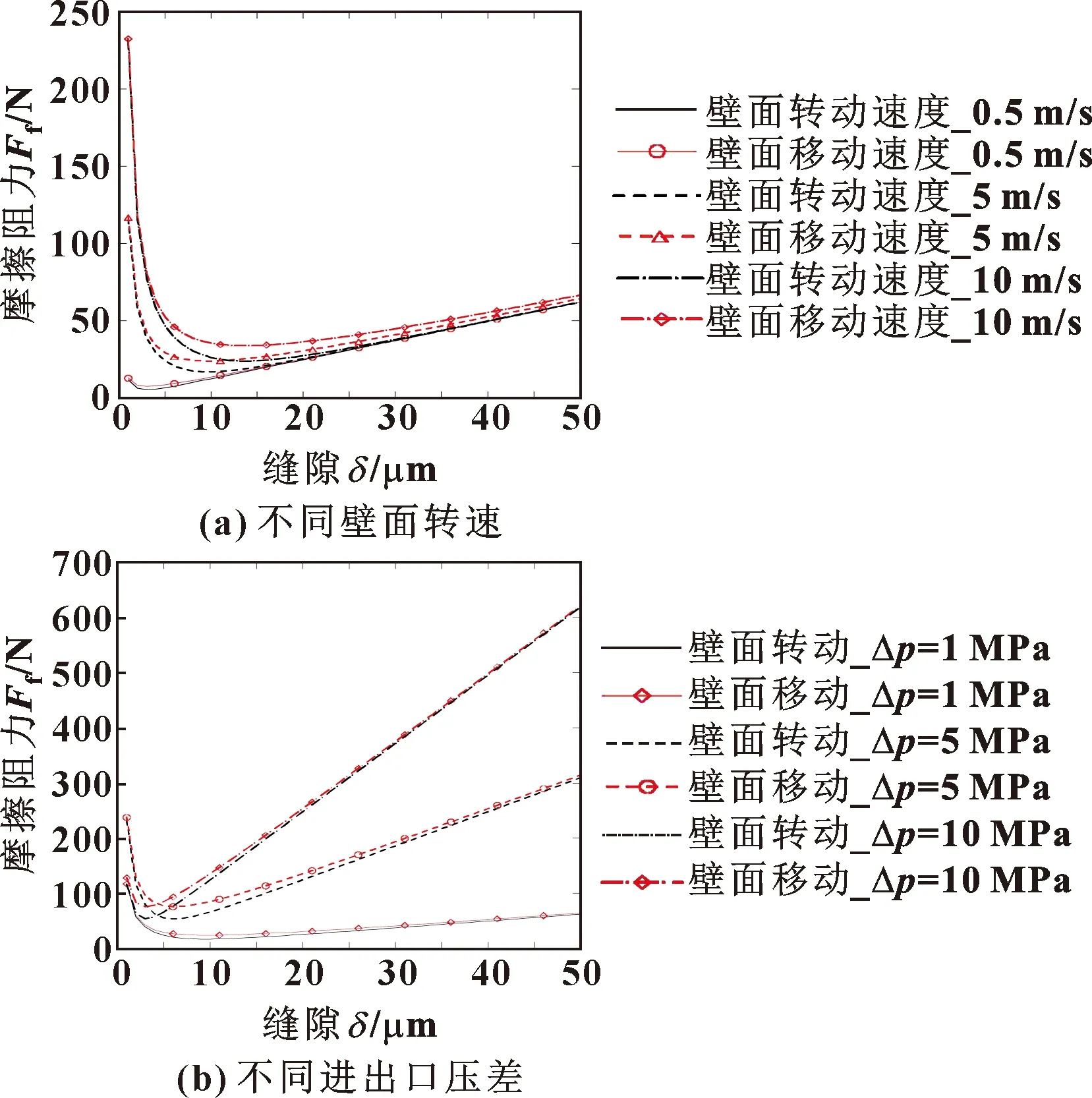
图3 二元缝隙流动摩擦阻力随缝隙变化曲线
3 模型建立及数值仿真
3.1 仿真模型及条件
针对10通径2D伺服阀阀芯最右侧台肩与阀套配合的缝隙流尺寸建立仿真模型如图4所示,流体模型在Meshing下进行六面体网格划分。将网格导入Fluent 21.0进行条件设置,定义好入口、出口、静壁面(外壁面)和动壁面(内壁面)。

图4 二元环形缝隙流模型
设定仿真条件如下:缝隙δ为0.005、 0.02、0.04、0.06 mm;入口压力p1为1、5、15、30 MPa;动壁运动速度ω为 0.35、0.7、3.5、7、14 rad/s。
3.2 仿真结果
图5是环形缝隙为20 μm时,入口压力5 MPa、出口压力为0.1 MPa、壁面转速7 rad/s情况下壁面压力分布云图和动壁面的速度矢量图。可以看出:压力从入口到出口呈递减趋势。速度箭头在压差流和壁面转速的牵引下呈螺旋变化方向。
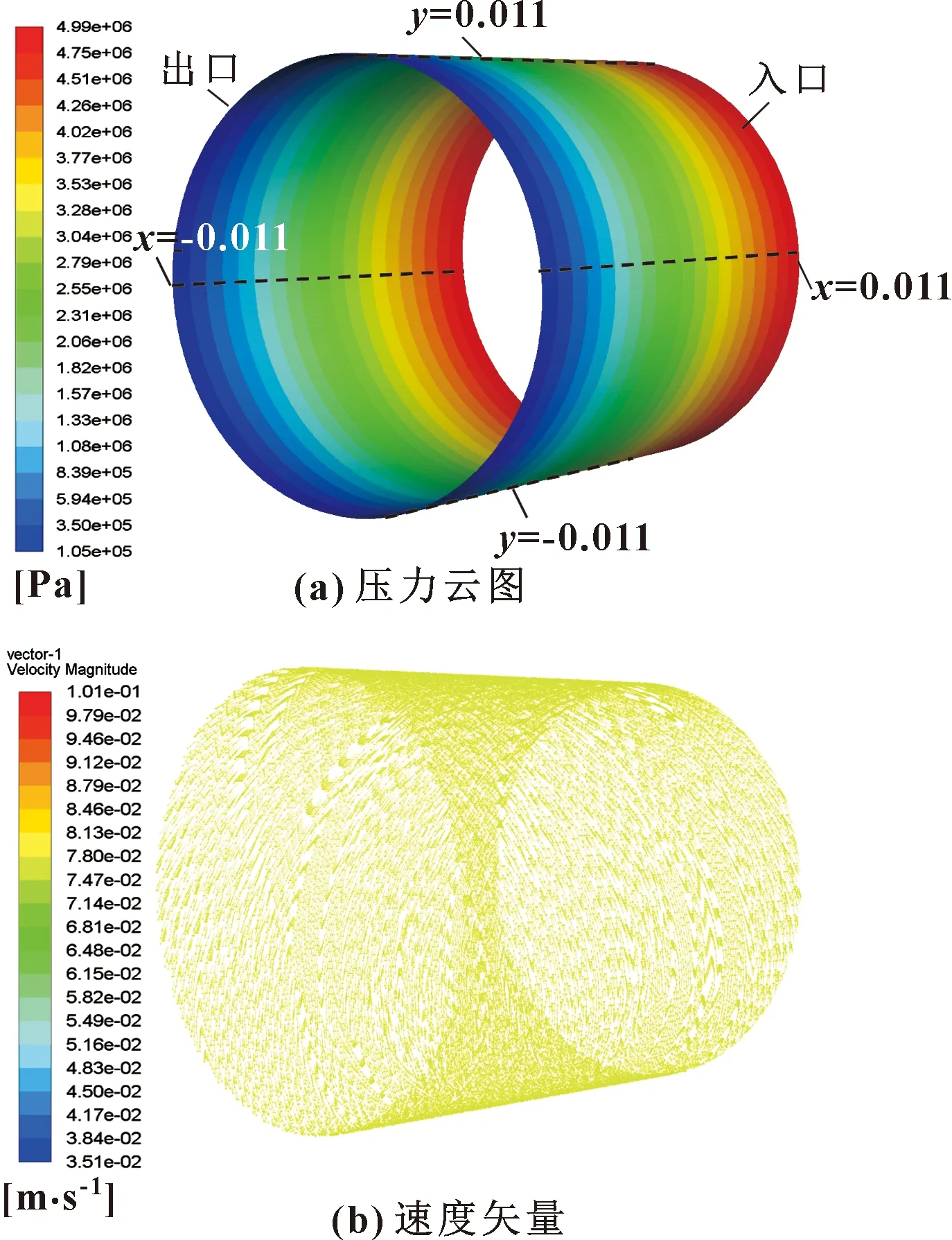
图5 二维缝隙流仿真
选取阀芯台肩壁面上的4条母线y=±0.011 m、x=±0.011 m,如图5(a)所示,提取其上的压力、流速参数作为参考值进行分析。在不同缝隙、入口压力及动壁面转速的情况下,阀芯台肩4条母线上的压力分布及其分布特点如下所述。
(1)缝隙宽度
同心条件下,阀芯角速度为7 rad/s,入口压力为5 MPa,缝隙宽度分别为8、10、20和40 μm时阀芯台肩上y=±0.011 m、x=±0.011 m 4条母线上的压力分布如图6所示。当缝隙宽度为8 μm时,4条母线上的压力分布变化较明显,且壁面处流速在轴向(z向)分布不均匀;缝隙宽度为20 μm和40 μm时,4条母线上的压力基本重合,且呈线性下降。
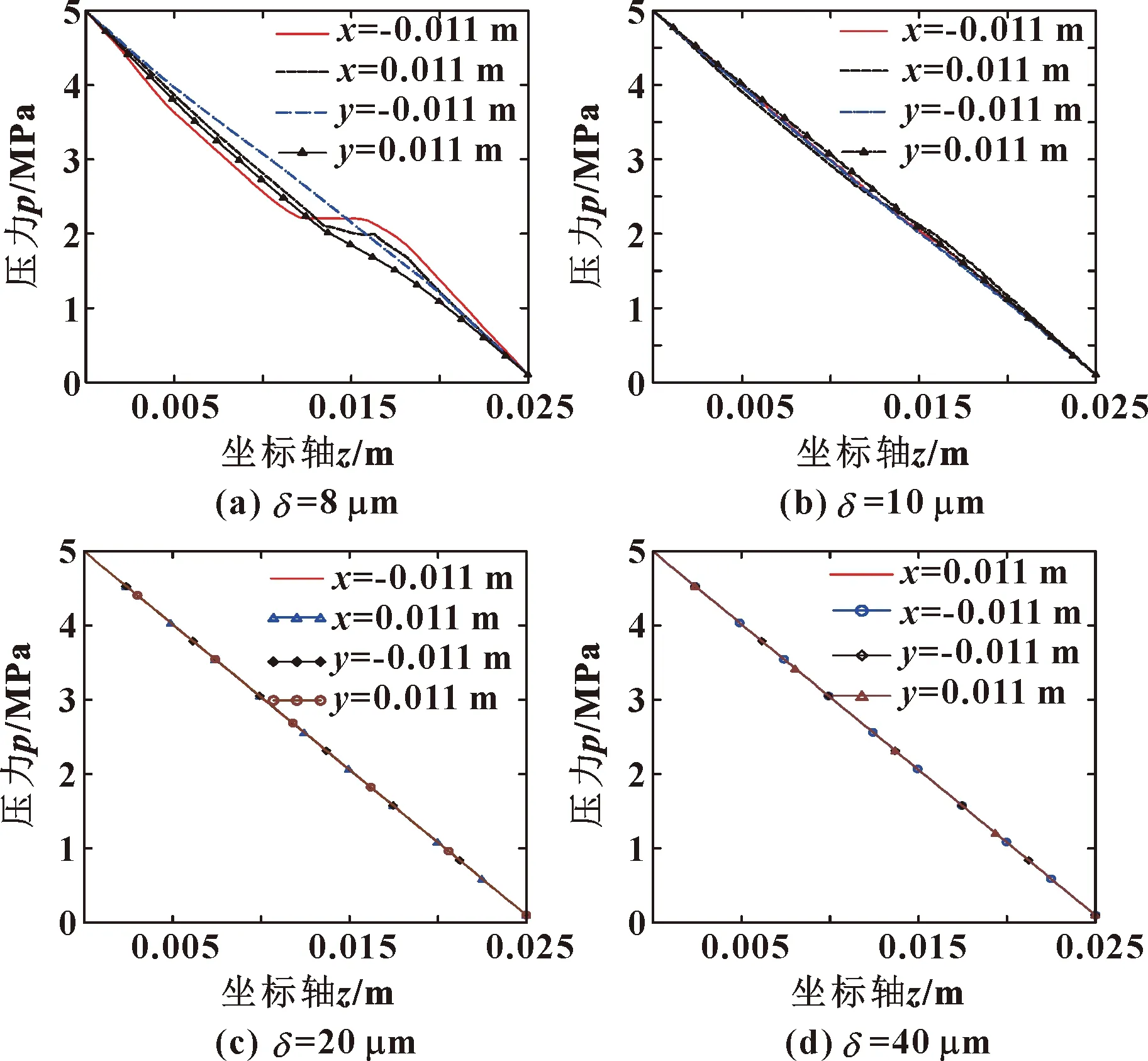
图6 不同缝隙时4条母线上压力分布
(2)壁面速度
图7所示为缝隙宽度为10 μm,入口压力为5 MPa,阀芯台肩角速度分布为0、3.5、14 rad/s时,阀芯台肩面4条母线上的压力分布。当缝隙宽度相同时,4条母线上压力变化趋势相似。

图7 不同角速度下4条母线上压力分布
(3)入口压力
图8所示为阀芯台肩角速度7 rad/s,缝隙宽度为10 μm,入口压力分别为1、10、15 MPa时,阀芯台肩面上4条母线的压力分布和流速分布。随着入口压力升高,4条母线上的压力变化幅值减小且趋于一致,母线上的流速受入口压力变化影响较弱。
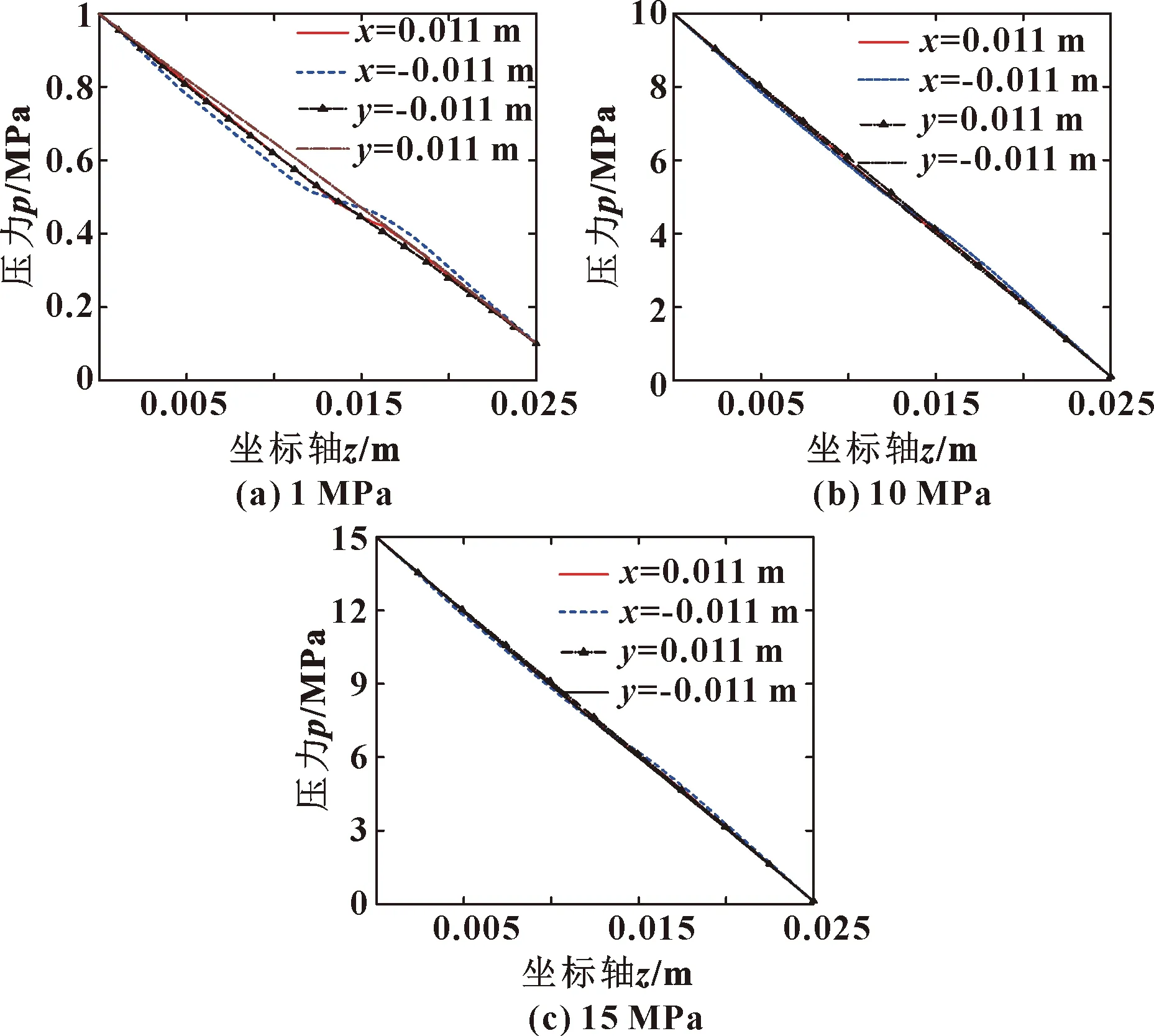
图8 不同入口压力下4条母线上压力分布
4 仿真结果讨论
将缝隙为10 μm,台肩角速度为7 rad/s,入口压力分别为1、5、10、15 MPa的仿真结果进行后处理后,提取阀芯台肩上因剪切流和压差流引起的摩擦力;同时提取缝隙为10 μm,入口压力为5 MPa,阀芯台肩角速度分别为0、3.5、7、14、21 rad/s情况下,阀芯台肩上所受摩擦力和入口压力为5 MPa,阀芯台肩角速度为7 rad/s,缝隙宽度分别为8、10、20、40 μm时,阀芯台肩所受的摩擦力,如表1所示。

表1 入口压力、缝隙、阀芯角速度与摩擦力关系
由表1可知:当缝隙宽度相同时,台肩上所受二元缝隙流的摩擦力随入口压力增加而增加,随阀芯角速度增加后出现最大值后呈下降趋势。当缝隙宽度增加,摩擦力急剧下降,当缝隙宽度增至40 μm时,摩擦力基本可以忽略不计,但此时缝隙的泄漏量会急剧增加。
5 实验研究
5.1 实验装置
二维伺服阀设计时,其阀芯阀套间的缝隙根据配合要求在2~6 μm之间。为测量二维伺服阀阀芯启动阻力,在拨杆侧边距离阀芯轴线L处放置一磁钢,通过激光位移传感器测量阀芯启动时拨杆侧向位移,如图9所示,将位移经过2次微分处理后计算出切向加速度,根据阀芯力矩平衡计算出阀芯启动时的阻力。
5.2 启动阻力实验
当系统压力为5 MPa时,将计算机输出频率为0.1 Hz的矩形波作为伺服阀电机驱动信号,驱动阀芯往复运动,通过测试系统测得阀芯摆动位移波形如图10(a)所示。
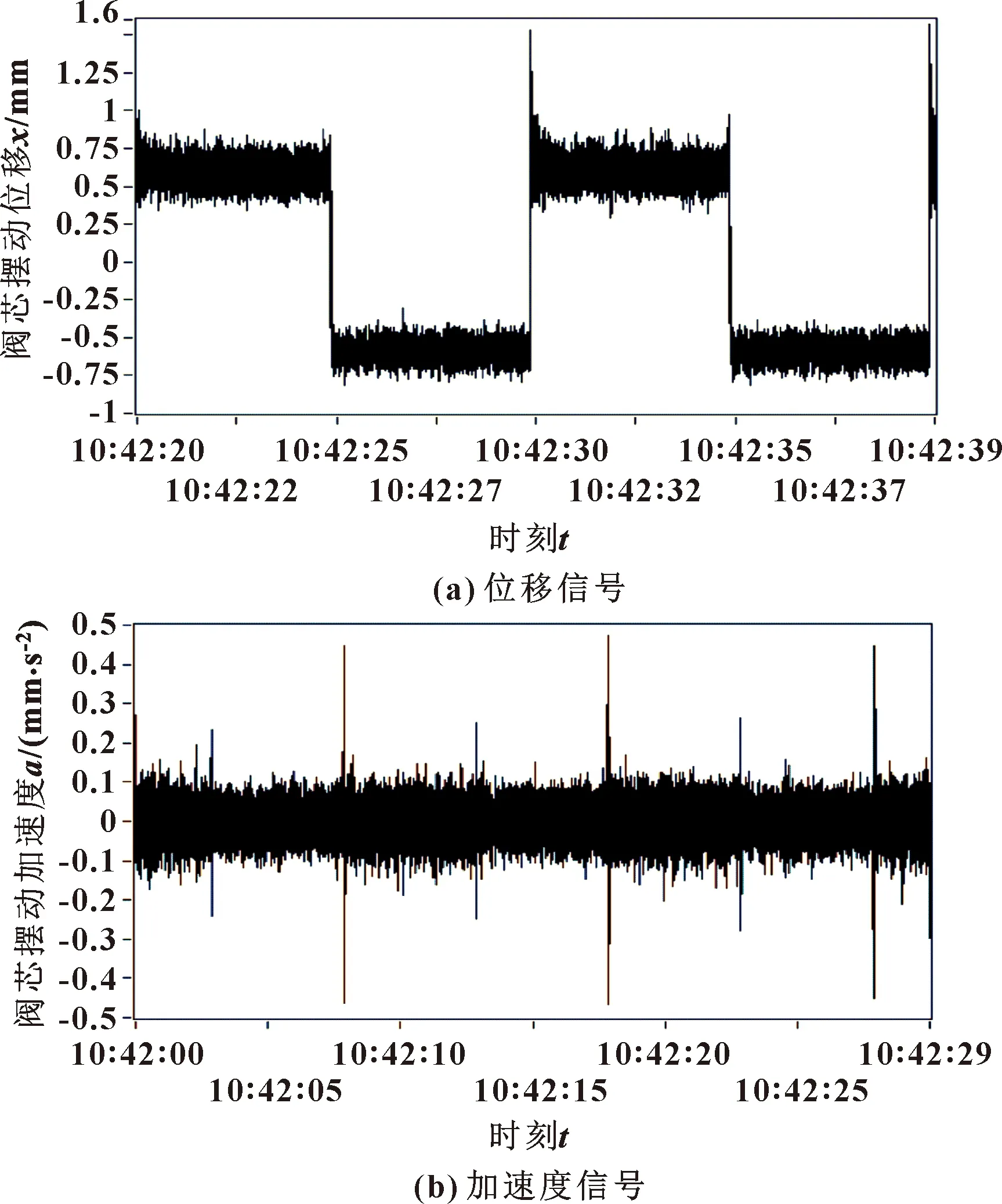
图10 阶跃响应时阀芯信号波形
以阶跃响应上升时间作为阀芯从一侧到另一侧所经历的时间,上升时间ts=0.01 s,阀芯转过角度为2.88°,摆动测量位置至阀芯中心的距离L为26 mm,因此,阀芯转角放大至测量位置处,转过的总弧度sc为
sc=θL=1.3×10-3m
因转角很小,与测量对应的弦长基本相等,故认为激光位移传感器测试所得弦长变化为阀芯弧长变化。伺服阀阀芯和拨杆通过夹紧装置进行固定,经测量两部分质量综合ms共计52.5 g。
将阶跃响应的位移信号经过两次微分,得到如图10(b)所示的加速度信号,切向加速度as在启动阶段值为0.45 mm/s2。
拨杆在推动阀芯摆动时,受到电机通过拨轮施加给拨杆的驱动力Fa,因拨杆和阀芯之间通过夹紧装置固定,故拨杆所受的阻力为阀芯周向产生的摩擦力Ff,如图11所示。因阀芯摆动范围很小,通过磁钢处所测得位移,经处理后得到惯性力对应的切向加速度as。

图11 拨杆受力分析
根据达朗贝尔原理,任意时刻,旋转物体的惯性力矩、施加的外力矩和约束力矩平衡,得:
kFaLa-FfR=FlL=mlasL
(13)

用力矩方式表达:
Maη-Mf=mlasL
(14)
式中:Ma为驱动力矩,N·m;Mf为摩擦阻力矩,N·m。
由式(13)和(14)得:
Ff=(ηMa-mlasL)/R
(15)
在阶跃响应实验中测得电机的驱动扭矩Ma约为0.02 N·m,取拨轮和拨杆间的效率为0.92,将已知参数代入式(15)得摩擦力Ff=2.94 N,可见旋转摩擦阻力与轴向摩擦阻力相比要小很多,故2D伺服阀可以选用功率较小的电机械转换装置。
6 结论
(1)通过运用二元缝隙流动理论,建立了二维液压阀启动时缝隙流场内剪切压力分布公式,通过计算得二维液压阀最小摩擦力允许的缝隙小于同情况的一元流动;
(2)建立了二元缝隙流仿真模型,验证了动壁面上摩擦阻力与缝隙宽度、入口压力和壁面角速度关系密切,与理论结果吻合;且随着缝隙宽度增加,摩擦阻力急剧下降,随着入口压力增加有明显增加趋势,随着壁面角速度增加,摩擦阻力增大后有减小趋势;
(3)通过实验验证了二维伺服阀启动时需要克服的启动摩擦阻力很小,在5 MPa系统压力下,启动摩擦阻力仅为2.94 N,由二维伺服阀工作原理知,一旦阀芯克服摩擦阻力发生旋转运动,伺服阀主阀口在液压力的驱动下就会打开,因此,二维伺服阀可以实现比传统伺服阀更大的功率质量比。
