双定子力偶型摆动多路马达的径向受力特性
2023-08-17吕世君朱鸿飞苗宇航闻德生
吕世君,朱鸿飞,苗宇航,闻德生
(燕山大学机械工程学院,河北秦皇岛 066004)
0 前言
目前,大多数马达受限于原理,在工作时一侧输入高压油,另一侧排出低压油,马达除受力矩驱动工作外,还在高压侧受到很大的侧向力,这导致了马达径向受力不平衡[1-2]。伴随着液压向高压化方向发展,不平衡的径向力带来的问题日益突出[3]。一方面,马达工作压力受到限制;另一方面,泵内零件在复杂交变载荷的影响下会加速疲劳损坏,这也是马达的实际使用寿命降低的原因之一[4-5]。为了降低径向力不平衡带来的损害,力矩马达在设计时不得不提高零件的强度,势必增加马达零件的结构尺寸[6-8]。因此对马达的径向力进行分析,无论是在理论还是工程上都有着重要的意义。
双定子双作用力偶马达有1个转子和内外2个定子,可以形成内外2种马达,增加了马达的输出方式。其在原理上平衡了径向力,可以实现力偶式的转矩输出[9]。但由于双定子双作用力偶马达具有多输入和可以差动连接的特点[10-11],并不是每种连接方式都能完全平衡径向力,因此本文作者对双定子双作用力偶马达不同工作方式的径向力进行分析,为今后更进一步的研究工作奠定基础。
1 双定子双作用力偶马达工作原理
文中以双定子双作用力偶马达中的摆动马达为例,对各种工作方式下的径向力进行分析,如图1所示为双定子双作用摆动马达基本结构。

图1 双定子双作用摆动马达结构
双定子双作用摆动马达利用1个内定子、1个外定子、1个转子和两侧端盖在一个壳体内形成了内外2种马达:外定叶片、外动叶片、外定子、转子和两侧端盖封闭形成外马达;内定叶片、内动叶片、内定子、转子和两侧端盖封闭形成内马达。同时,根据作用数n的不同,内外马达均被定叶片分隔形成n个独立马达。2n个马达的进出油口均单独布置,互不干扰。在马达工作时,既可以单独驱动内马达或外马达工作,又可以同时驱动内外马达联合工作。并且由于内外马达排量不同,还可以实现差动工作。如图1所示,双定子双作用摆动力偶马达有A—D 4个外密闭腔室和a—d 4个内密闭腔室。
2 马达的工作方式分类
2.1 外马达单独工作
如图2所示,建立直角坐标系,以逆时针方向为正方向,外马达单独工作时,转子上的径向力为直接作用在转子上的液压力FW。

图2 外马达单独工作
分析可知正转时第i个外马达工作时转子上径向力为
(1)
(2)
反转时高压区弧长由R2θ变为R2(2π/n-4α-θ),合力与x轴正向的夹角由[θ/2+α+2(i-1)β]变为[θ/2+3α+(2π/n-4α)/2+2(i-1)β],反转时转子上径向力公式为
(3)
(4)
式中:B为摆动马达叶片宽度;p0为进油口油液压力;R2为外动叶片根圆半径;θ为摆动马达转动角度,0≤θ≤2π/n-4α,2α为马达叶片所占角度,n为马达作用数;2β为马达相邻定叶片中心线之间的夹角。
2.2 内马达单独工作
如图3所示为内马达单独工作状态,此时转子上的径向力为直接作用在转子上的液压力FN。
同理可知,正转时第j个内马达单独工作时转子上径向力为
(5)
(6)
反转时有:
(7)
(8)
式中:R3为内动叶片根圆半径。
2.3 联合工作
如图4所示为内外马达联合工作,设此时转子上的径向合力为FL。为简化分析,只考虑马达数量对径向力大小的影响。
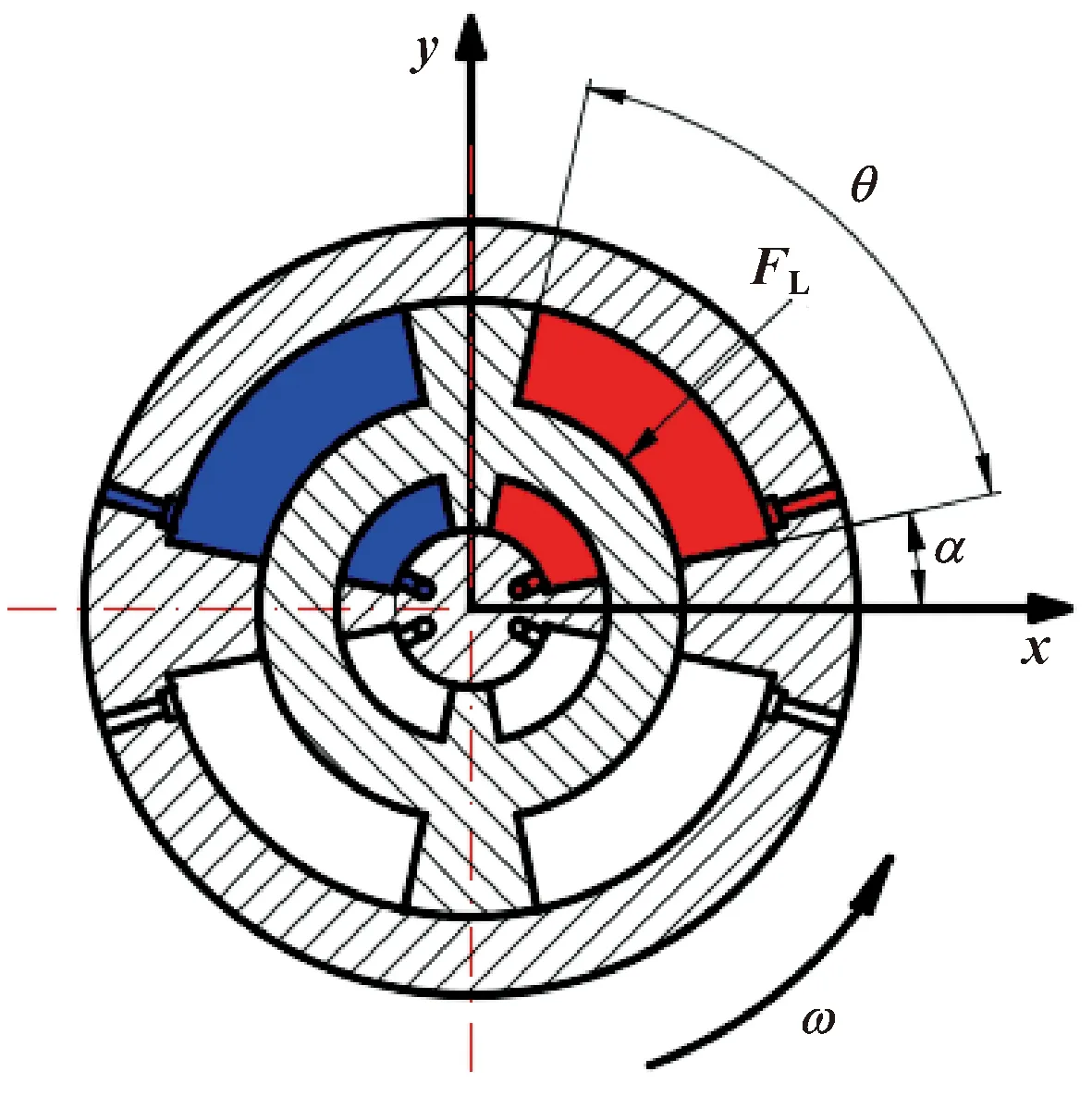
图4 联合工作
内外马达联合工作时,转子上的径向力为
(9)
(10)
正转时有:
(11)
(12)
(13)
(14)
式中:β为马达相邻叶片之间1/2夹角;k1为工作的内马达个数(k1≤n);k2为工作的外马达个数(k2≤n)。
类似地,将反转时高压区弧长及合力与x轴正方向的夹角代入公式(11)—(14),替换正转时的弧长及合力与x轴正方向的夹角,同样可得反转时内外马达在x、y方向上的合力。
2.4 差动工作
如图5所示为内外马达差动工作,设此时转子上的径向合力为FC。同样只考虑马达数量对径向力大小的影响。
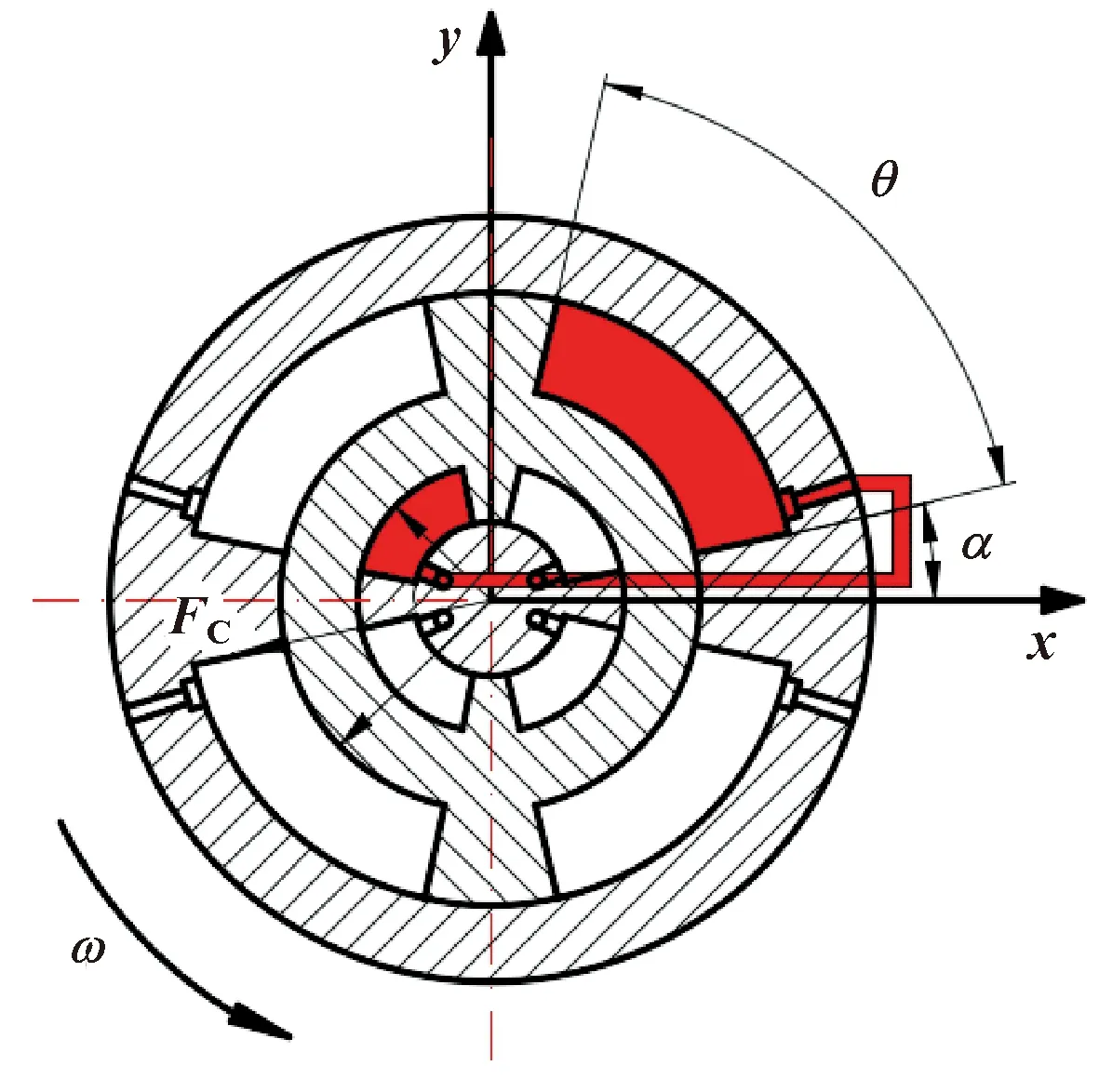
图5 差动工作
当内外马达差动时,正转状态下,外马达高压区弧长为R2θ,与x轴正向夹角为[θ/2+α+2(i-1)β]。此时内马达弧长为R3(2π/n-4α-θ),与x轴的夹角变为[θ/2+3α+(2π/n-4α)/2+2(j-1)β]。代入内外马达径向力表达式中有:
(15)
(16)
(17)
(18)
反转时外马达高压区弧长为R2(2π/n-4α-θ),合力与x轴正向的夹角[θ/2+3α+(2π/n-4α)/2+2(i-1)β],内马达高压区弧长为R3θ,与x轴夹角为[θ/2+α+2(j-1)β]。代入内外马达径向力表达式中同样可得反转时内外马达在x、y方向上的合力。
转子上径向力为
(19)
(20)
各种连接方式下马达的径向力平衡状况如表1所示。
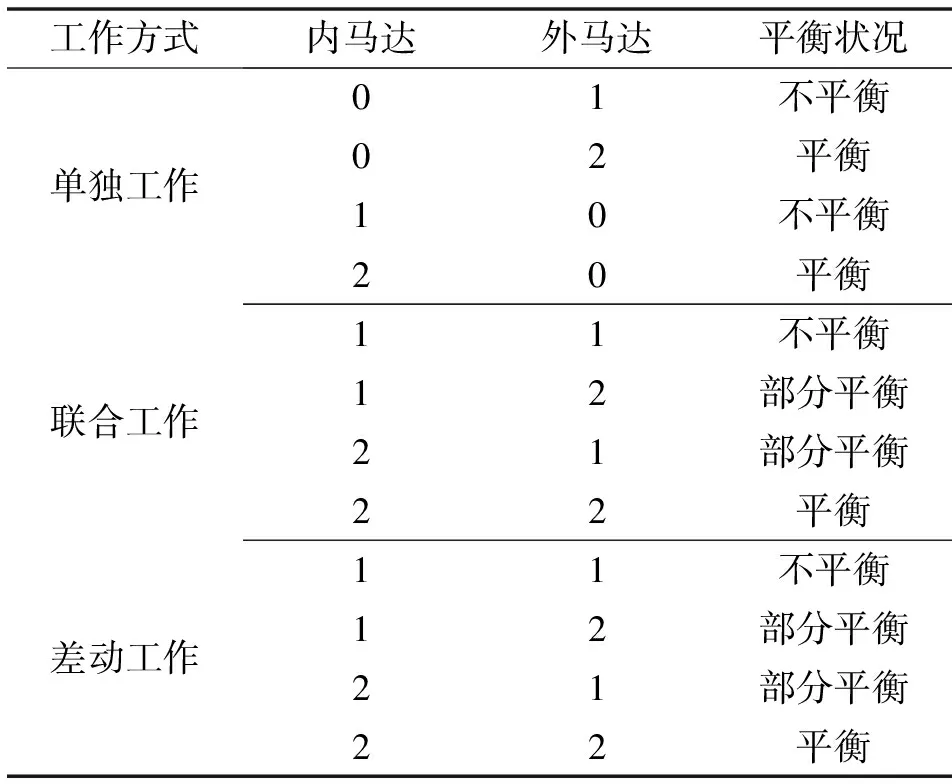
表1 马达不同连接方式下的径向力
3 仿真分析
设计马达叶片厚度B为40 mm,外动叶片根圆半径R2为40 mm,外定叶片根圆半径R1为50 mm,内动叶片根圆半径R3为26 mm,内定叶片根圆半径R4为18 mm,进出油口压差p0为6.5 MPa,马达最大摆动角度为7π/12,运用MATLAB对马达的径向力进行仿真分析可以得到如图6—8所示结果。
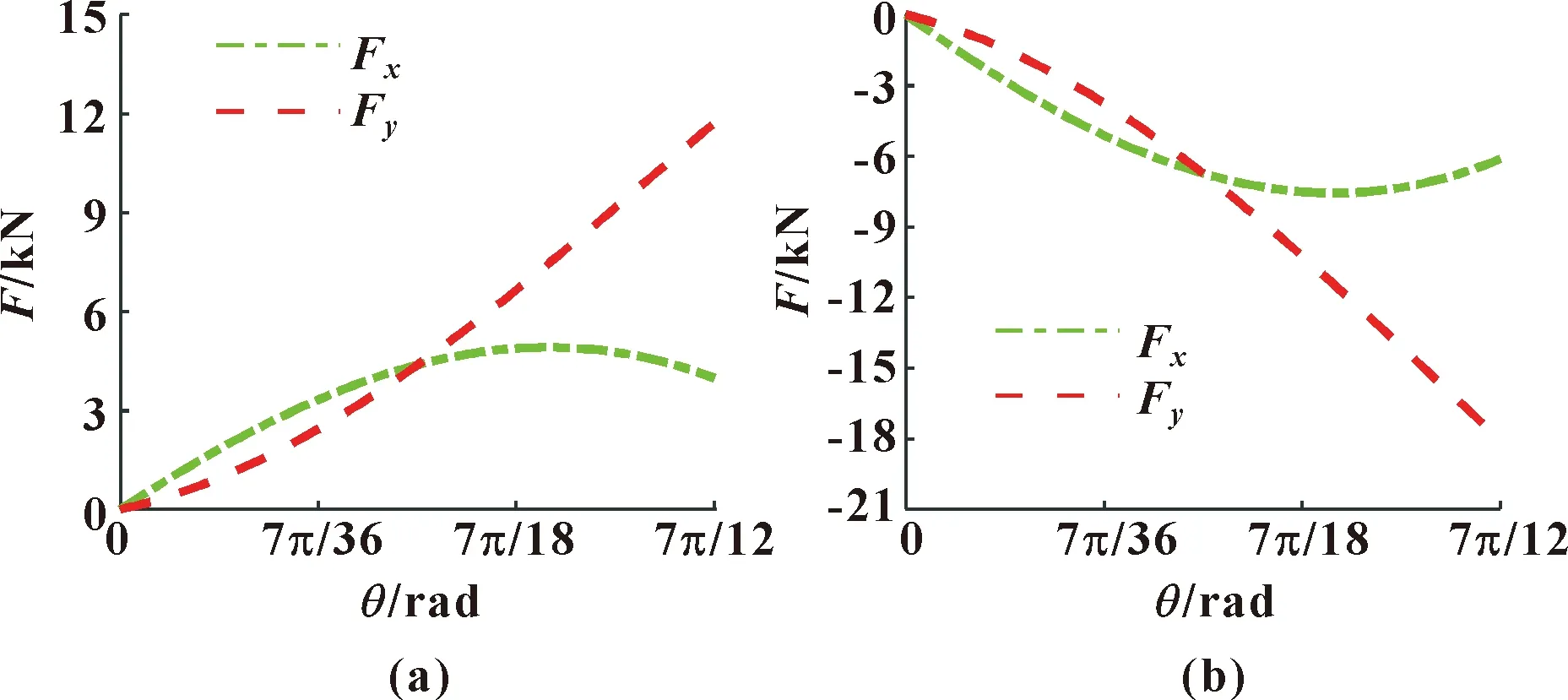
图6 内马达(a)、外马达(b)单独工作时径向力
单独工作状态下有2种径向力不平衡的工作方式,对内外马达单独工作状态下的径向力进行分析。内马达单独工作时,以正转高压油输入a,反转高压油输入b为例;外马达单独工作时,以正转高压油输入A,反转高压油输入B为例。由于马达反转时,转子上径向力大小的变化规律相同,仅方向不同,所以后面仅分析马达正转时的转子径向受力状态。在正转状态下转子上径向力变化情况如图6所示。
对联合工作状态下的径向力分析,存在1外马达1内马达、1外马达2内马达以及2外马达1内马达3种径向力部分平衡的连接方式。由于1外马达2内马达联合工作的情况下,2个内马达的径向力相互抵消,只剩1个外马达的径向力,与1外马达单独工作时的径向力情况完全相同;同理,2外马达1内马达联合工作的情况下,所受的径向力与1内马达单独工作时相同,所以此处仅绘出1外马达1内马达联合工作时的径向力图像。
由于每个马达进出油口均独立设置,因此1外马达1内马达联合工作同样存在2种情况:一种是内外马达无相位差,以正转高压油输入A、a为例;另一种是内外马达存在相位差2β,以正转高压油输入A、c为例。在正转状态下马达转子上的径向力变化情况如图7所示。
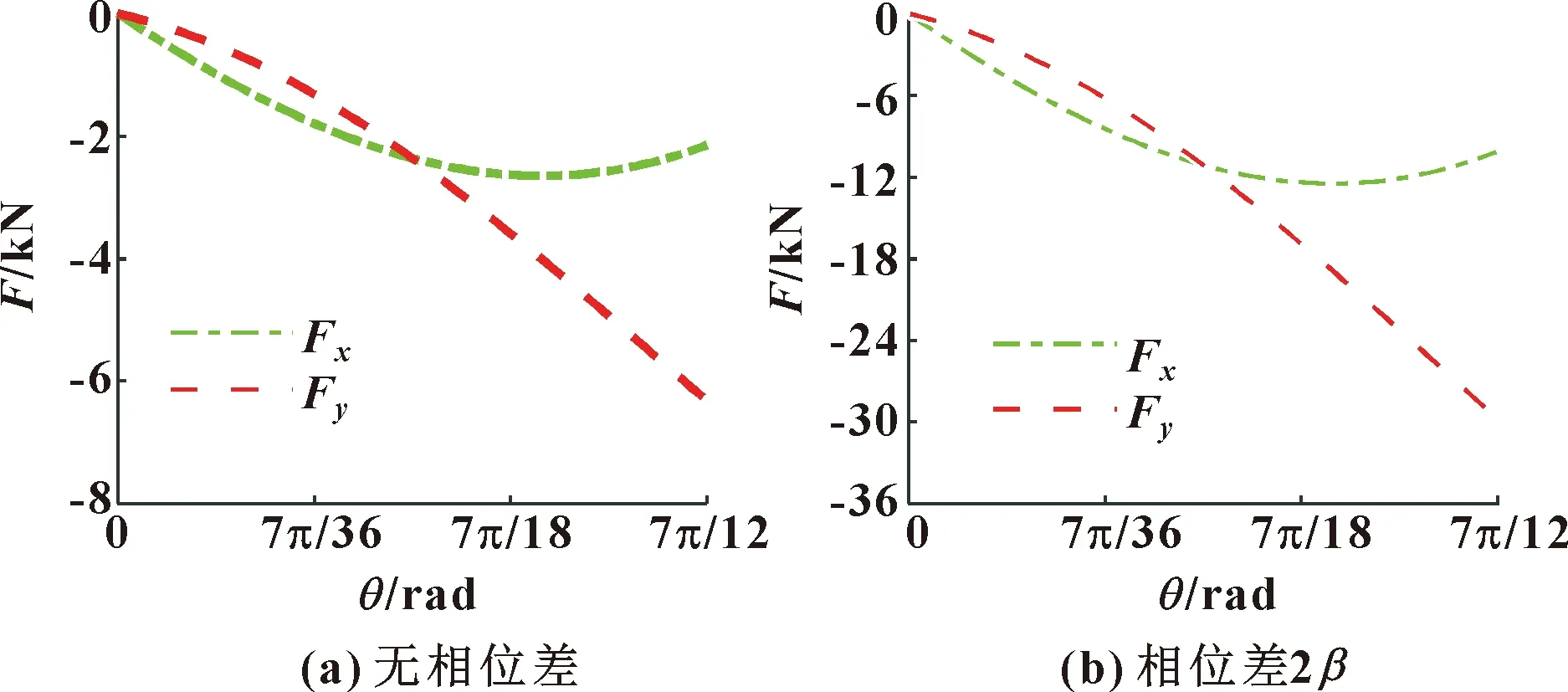
图7 1个外马达1个内马达联合工作径向力
通过图7可以看出:1内马达1外马达联合工作时径向力的大小与内外马达工作腔之间的相位差有关,当无相位差时两者产生的径向力相互抵消,减小了径向力的波动,当存在相位差时,径向力出现叠加增强的情况。对比图7和图6不难发现:径向力的大小同时受到内外马达个数和相位差的影响,当无相位差时,转子上的径向力受到一定程度的抵消,甚至小于部分平衡状况下的径向力。
对内外马达差动工作状态下的径向力分析,存在1种径向力不平衡的连接方式,即1外马达1内马达,以A、b 2个腔室工作为例;存在2种径向力部分平衡的方式,即1外马达2内马达、2外马达1内马达。由于这2种差动情况下径向力部分平衡,与单个内马达、单个外马达工作时径向力状态相同,所以此处仅绘出1外马达1内马达联合工作时的径向力图像。在马达正转时转子上径向力变化情况如图8所示。
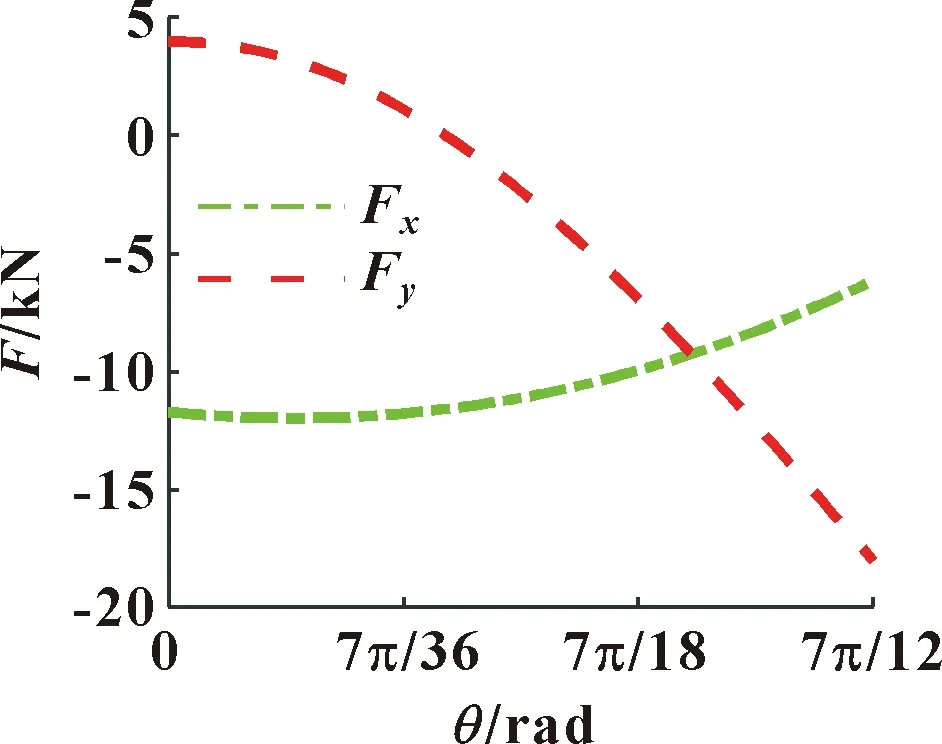
图8 1外马达1内马达差动工作径向力
4 结论
(1)相较于传统的单输出马达,双定子双作用摆动马达有12种输出方式,不但可以单马达输出,还可以内外马达联合输出、差动输出,大大丰富了马达输出转速转矩的种类。
(2)双定子双作用摆动马达每种输出方式下的径向力情况都有所不同,一共存在4种径向力完全平衡,4种径向力部分平衡以及4种径向力不平衡的连接方式。为减少径向力波动对马达的影响,应尽量选取径向力平衡的方式进行输出。
(3)对双定子双作用摆动马达而言,转子上的径向力在部分平衡的状况下,不一定比不平衡的状况小。马达在同一种连接方式下(如1内马达1外马达)的径向力大小还受内外马达之间相位差的影响。显然,差动工作也存在类似的情况。
