落实核心素养,彰显价值导向——近两年高考试题的特点例析及教学启示

李朋飞 容 兰

(合肥市第八中学 安徽合肥 230000)

国之大计,教育为本。培养能够担当民族复兴大任的时代新人是党对教育工作者的基本要求。习近平总书记在党的二十大报告中明确指出,教育要坚持为党育人、为国育才。身处一线的教育工作者,除了努力学习理论知识、提升教学水平,还要多进行教学探索,接触和实践新课程理念,适应新时代教育改革对教师的期望和要求。笔者现以2021年、2022年高考理科综合全国乙卷第25题为例,剖析、分享全国卷高考试题的考查特点、载体和方向,以期对教育教学有一定的引导和促进作用。

一、真题回顾

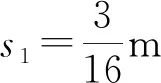
(1)金属棒在磁场中运动时所受安培力的大小;

(2)金属棒的质量以及金属棒与导体框之间的动摩擦因数;

(3)导体框匀速运动距离。

2．(2022年全国乙卷第25题)如图(a),一质量为m的物块A与轻质弹簧连接,静止在光滑水平面上:物块B向A运动,t=0时与弹簧接触,到t=2t0时与弹簧分离,第一次碰撞结束,A、B的v-t图像如图(b)所示。已知从t=0到t=t0时间内,物块A运动的距离为0.36v0t0。A、B分离后,A滑上粗糙斜面,然后滑下,与一直在水平面上运动的B再次碰撞,之后A再次滑上斜面,达到的最高点与前一次相同。斜面倾角为θ(sinθ=0.6),与水平面光滑连接。碰撞过程中弹簧始终处于弹性限度内。求

(1)第一次碰撞过程中,弹簧弹性势能的最大值;

(2)第一次碰撞过程中,弹簧压缩量的最大值;

(3)物块A与斜面间的动摩擦因数。

二、高考试题分析和特点

2021年全国乙卷第25题考查的知识主要有:受力分析、匀变速直线运动规律、牛顿运动定律、功、磁场以及功能关系。同时,学生需要具备以下能力:推理能力、运算能力、理解能力、信息提取加工能力、分析综合能力。

2022年全国乙卷第25题考查的知识主要有:动量守恒定律、能量守恒定律、牛顿运动定律、运动学规律和v-t图像等。同时,学生需要具备以下能力:理解能力、模型构建能力、推理论证能力和理论探究能力。

这两道题在试卷中的作用相同,均具有良好的区分功能,在学科素养考查方面,均涉及运动分析和受力分析,能量的转化和能量守恒思想,要求学生具备基本的物质观、运动与相互作用观、能量观。在学科思维能力考查方面,该题考查的重点包括模型构建、科学推理和科学论证等。在科学探究方面,学生需要根据题意和运动分析,进而通过“问题—猜想—求证—解决”的科学推理过程,得出最终结论。这两道试题综合性较强,对学生学业水平能力要求较高。

纵观近几年高考试题全貌不难发现,高考试题呈现以下几个明显特点:

(一)深化基础性,加强综合性考查

高考试题功能之一就是导向性。近年来,高考试题命题特点逐渐从知识和能力立意转向素养导向、价值体现,立足于基础知识,加强了知识点间、关键能力间以及知识点与能力间的联系。比如理科综合2021年全国甲卷的第19题、第22题和2022年全国乙卷的第19题、第22题等,均呈现出基础性,但又综合考查学生模型构建能力、理解推理能力等,体现了高考试题的综合性特点。

(二)深化试题情境,强化应用性考查

高考评价体系明确试题特征之一就是情境载体是考查能力和素养的串联线。2019年《中国考试》第12期发表了来自教育部考试中心命题中心的系列文章——《考试内容改革实施路径》,强调各学科均以真实情境作为试题的核心载体。利用真实情境设计试题,能够提升学生利用所学知识解决生活生产中实际问题的意识,增强学生灵活运用所学知识的意识,避免学生机械刷题。如理科综合2022年全国甲卷第14题、2022年全国乙卷第18题、2023年2月四省联考(云南、安徽、吉林、黑龙江)第20题,均以情境为载体进行基础性知识的考查,且呈现出试题和情境的深度融合趋势。

(三)经典试题改编,突出数理推理能力考查

纵观近些年高考理科综合全国卷不难发现,许多高考试题都能从前些年的高考真题中找到高度类似的试题。比如2022年全国乙卷第16题与2017年全国新课标Ⅱ卷第14题、2014年全国新课标Ⅱ卷第17题所涉情境完全相同,2021年全国乙卷第21题与2011年全国新课标卷第21题几乎完全一样,2021年全国乙卷第16题与2013年全国新课标卷第13题也是几乎相同。试题的高度相似之处还体现在试题本身注重考查学生的数学运算能力、推理论证能力。

(四)落实核心素养,凸显价值导向

习近平总书记一直在强调,中国特色社会主义新时代需要大量的创新型、应用型人才。随着科技发展和我国综合国力日益强盛,依靠机械刷题取得应试高分的“人才”已经不足以满足社会发展和科技创新需求。在教育高质量发展的蓝图下,随着教育改革的不断推进和深化,高考试题明显趋向于考查学生的核心素养和关键能力,少量试题对学生的思维品质考查要求较高。

三、高考试题特点对教学的启发

(一)重视对规律和原理的过程分析

对于复杂的物理过程问题,我们通常将其分解为几个小问题或者分解成几段简单的过程,然后厘清每个过程所涉及的物理规律和原理,适用的不同观念和方法,之后再把每个过程串联起来,形成完整的解题过程。例如前文中的2021年全国乙卷第25题,可以将导体棒和导轨的运动分成三段:第一段是导体棒从开始运动到进入磁场之前,第二段是导体棒进入磁场后因受到安培力而做匀速运动的过程,第三段是导体棒出磁场之后导轨在磁场中匀速运动直到导体棒与导轨共速的过程。将整段运动分解为三段,则每一段的难度都有所降低,可以有效帮助考生实现逐个击破,达到解决问题的目的。

在平时的学习中,学生容易步入对物理规律和定理死记硬背的歧途,而忽视了对物理运动过程和物理规律的分析,如受力分析、运动过程分析和功能关系分析等。教师应该在平时课堂教学活动中提醒学生不要机械刷题和死记硬背,引导学生理解和掌握规律和原理的来龙去脉。这样的教学不仅能有效促进学生接受和理解物理知识,更有利于学生形成自主学习、常反思总结的良好习惯,进而养成科学、持久的学习力。

(二)重视物理模型的构建

高中物理规律和原理往往非常抽象,处理问题的过程又比较复杂。学生可以通过构建模型来帮助自己更加高效地理解物理概念,掌握物体运动规律。模型构建能力是学生形成科学思维的基础,然而不少学生在解决物理问题的时候缺乏模型构建的意识。在日常教学中,教师需要注意引导学生提升构建模型、识别模型、运用模型的能力,并加强对模型构建和识别能力的训练。历年来高考均有试题涉及斜面模型、滑块模型、单杆模型、超失重模型、连接体模型、人船模型、理想气体模型、简谐振动模型等,所以在教学过程中,教师须注重引导学生做到准确识别模型、学会构建物理模型、顺利运用模型解决具体问题。学生在增强模型构建意识的同时,也在锻炼自己解决实际问题的能力。

(三)重视思想方法的积累

人们在研究物体运动规律和物理原理的过程中所积累下的一系列的科学认知方法,经过完善和反复修改、总结以后就成了今天我们所熟悉的物理学的定理、定律以及思想方法。起源于生活中的现象、规律、物理原理所总结而来的这些物理学思想方法,同时又能够帮助人们去探索和解决未知的物理问题。中学物理思想方法是求解物理问题的重要依据,同时也是解决物理问题的基础方法。将物理学观念原理、思想方法、策略技巧等应用于解决实际问题,可大幅提升问题解决效率和效果。

高中阶段接触的物理学思想方法有很多,常见的有图像法、整体法、隔离法、逆向思维、平均值法、比例法、极限思维、等效思想、微元法、类比思想、对称思想、守恒思想、猜想与假设法等,也有一些思想方法并不是特别常见,但是总能给人留下深刻的印象,如补偿法、旋转圆法、放缩圆法等,这些方法在解决特定类型的问题中效果非常显著。学生有效解决物理问题需要以对物理学思想方法的透彻理解和熟练应用为基础,教师在教学过程中,需要树立先进的教学理念,优化教学和课堂结构,帮助和引导学生理解和应用物理学思想方法,强化学生的推理和论证能力。

(四)重视数理结合的科学推理

数学方法是解决物理问题行之有效的工具,借助数学运算和推演,有效结合物理过程,可以高效地帮助我们解决物理问题。科学推理是物理科学思维的一种具体显示形式,我们通常可以根据一些判断或者假设,利用推演思维,得出另外一个或者多个结论,由于物理与数学思想都是非常严谨连贯的,所以在利用数理结合的思想进行推理论证的时候,需要非常严格的逻辑过程。

高中阶段数理结合的思想要求并不会太高,主要体现在数学运算逻辑和少量的数学推演,所涉及的数学知识和能力水平要求难易适中,但数学推演和数形结合的思想确实对物理问题的解决有显著的促进作用。常见的数学思想方法有:二次函数、基本不等式、三角函数、图像以及矢量图,其中物理上的微元思想,其实是典型的数学微分思想,将一段复杂的物理过程,化整体为分段,化连续为分立,在每一段微元过程中利用物理模型和思想方法解决问题,最终再通过累加的思想达到解决问题的目的。数形结合也是物理中常用的方法,可以帮助我们有效描述相应物理问题或者物理量的变化过程,具有简洁、直观、信息量大的特点。

种种方法和思想,启发我们教学不能简单地进行公式讲解,也不能单纯讲解题技巧,更不能采用题海战术进行教学或者训练,物理教学应该是从物理现象到物理学原理、从课堂情境到物理图景、从建立模型到形成思维能力、从接受知识到质疑创新……新时代物理课堂须深入浅出,环环相扣,步步为营,如此才能真正做到每一节物理课堂中都有物理学科核心素养理念的落实。