多元表征，促进学生数学深度学习

2023-08-12朱万春

小学教学研究·教研版 2023年7期

朱万春

【摘要】小学数学的概念教学是数学学习的一个难点。面积概念学习是学生第二学段空间形式认识发展的一次飞跃，弄清楚“面积是什么”对学生的数学深度学习有十分重要的意义。文章主要阐述经历动作表征，体验物体的“面”；经历图像表征，感悟物体的“面积”；经历言语表征，探索物体的“面积”，建立“面积”的模型，通过多元表征转换，从学生的生活视角出发发掘面积相关的数学问题，合理运用多元表征，深化对面积概念的理解。

【关键词】数学教学多元表征深度学习

数学多元表征是指在数学学习中，既有内隐的心理层面的知识整合与建构，也有外显的能够呈现认知过程和认知结果的多样化的数学表达。数学概念在教学中成为一个难点，多元表征的学习方式在概念教学上使用较多。

数学概念是客观现实中的数量关系和空间形式的本质属性在人脑中的反映。描述式概念是小学第二学段最主要的表示方式，笔者引导学生通过对动作、图像、言语等多元表征过程的学习，让学生经历概念生成、整理和归纳的过程，帮助学生真正领悟数学概念本质。下面笔者以苏教版三年级“认识面积”一课的教学为例，谈一谈教学中如何合理运用多元表征促进学生对数学概念的学习。

一、经历多元表征过程，建立“面积”的模型

基于“面积”概念的抽象，对学生的认知水平有一定的要求，笔者设计了“直观—体验—理解”的认知过程，引导学生从真实情境中直观发现身边的地面、黑板面、橱窗面、数学课本的表面等，从找“面”、摸“面”，到从抽象的长方形、正方形等平面图形中的识“面”。通过比一比、说一说等活动，初步体验什么是面的大小；运用图像表征，丰富面积概念的语言描述，拓展学生对面积的理性认识，深入理解面积的意义。

（一）经历动作表征，体验物体的“面”

小学生受思维发展和认知水平的局限，对一些概念难以认知和理解，教师可以创设真实的生活情境，直观可视地对“面”的概念进行演示，通过模仿引导学生动手操作等，丰富学生的直观感受，积累操作经验。

片段1：找一找，摸一摸

师播放视频。

师：他们在做什么？女生在打扫哪儿？男生呢？

生1：他们在劳动，女生擦黑板，男生拖地。

师：观察得真仔细！（师指黑板）老师手指指的就是（），黑板边框一周的总长就是黑板的（），手掌摸的就是黑板的（）。

“面”在生活中无处不在，你还能找到什么“面”？

生2：地面。

师：你真会观察，让我们一起来观察一下地面。

生3：课本封面。

师：你能到前面来“摸”给大家看一看吗？

生上台展示。

师：不着急，慢慢摸，从左边摸到右边，再继续，把封面的每个角落都要摸到。下面请同学们伸出手掌，我们一起来摸一摸桌面。还找到什么面了？

生（齐）：课桌面、椅子面……

真实的生活情境，拉近了师生的距离，可以激发学生的学习兴趣。

（二）经历图像表征，感悟物体的“面积”

《义务教育数学课程标准（2022年版）》指出，空间观念主要是对空间物体的形状、大小及位置关系的认识。学生对面积概念的理解比较陌生，已学周长的概念对于学生认识面积具有负迁移。学生在学习“物体面的大小就是面积”时，教师可以从实物或立体图形中抽象出图形、符号等，经过学生观察，将这些图像转化为数学思想表征，形成图像表征，让学生充分经历对“面”的大小的感知活动，结合实例形成对面积的真实体验。

片段2：初识“面积”概念

师：同学们找到这么多“面”，请你们仔细观察这些“面”，你们发现了什么？

生1：这些“面”的大小不同。

师：看来“面”有大有小，这些“面”的大小指的是什么？

生2：是面积。

师板书：面积。

师：今天我们就一起来研究面积。如班级橱窗面的大小就是橱窗面的面积。门面的大小就是门面的面积。数学课本封面的大小指的是……

生3：数学课本封面的面积。

师：咱们说了这么多“面”的面积，用一句话表达就是这些物体的“面的大小”，就是这些物体“面”的面积。

师：请同学们也找2个“面”，比一比它们面积的大小，和同桌说一说。

生交流。

师：刚才我们比较出了许多“面”面积的大小，蒙上眼睛你还能比出来吗？接着我们来玩摸“面”的游戏。

学生通过图像表征从平面到立体，空间想象物体面积的表征，从规则到不规则物体，由立体实物抽象出图像，在比一比、说一说等活动中初步体验面积的概念，完善学生对面积含义的理解，感受数学学习的快乐。

（三）经历言语表征，探索物体的“面积”

通过互动交流、合作探究，教师引导学生在找一找、摸一摸、比一比的过程中用数学语言描述“面的大小”“面积的意义”，用言语表征简约、精确地描述物体面积，构建“面积”概念；引导学生感悟数学与现实世界的交流方式。

片段3：在比较中巩固“面积”概念

师：现在我们知道了物体表面的面积有大有小，下面请同学们将刚刚摸的“面”画下来。

生展示（图略）。

师（小结）：这些平面图形也有各自的大小，所以平面图形的大小就是平面图形的面积大小。我們挑几个来研究。

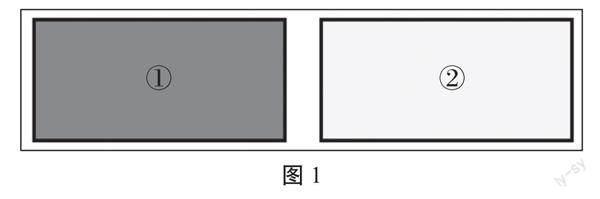
（1）对比图1中两个图形的相同之处。

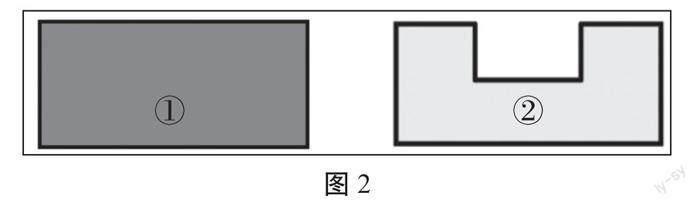
（2）比较图2中两个图形的不同之处。

小结：周长研究的是线的长短，面积研究的是面的大小。

在“面积”概念形成的过程中，引入生活“真实情境”，基于三年级学生的心理发展，引导学生经历动作表征、图像表征后，使学生通过言语表征，建立“面积”概念。教师出示两组图形，搭建引发冲突的脚手架，让学生在判断、重构中感受面积与周长的不同，培养学生从具象图形认知“面”有大有小，面积也有大小。

二、重视表征转换，内化“面积”的理解

动作、图像、言语等不同表征的转换呈现了学生不同的思维角度和水平。“认识面积”教学显然运用了多元表征，如动手操作、图像表示、言语解释与学习背景等都有直接的联系。同时，学生学习需要高阶思维层次的符号、数据等表征进行交流反馈，进一步促成各種表征的转换，建立不同表征的认知联结，经历面积大小的度量过程，初步感知面积度量单位统一的必要性，形成量感。

（一）运用多元表征，内化“面积”度量

《义务教育数学课程标准（2022年版）》指出，符号意识主要指能够感悟符号的数学功能，量感主要指对事物的可测量属性及大小关系的直观感知，符号意识和量感是形成抽象能力的经验基础。运用图像、符号多元表征在面积大小比较中可以结合符号表征对可测量图形的大小关系进行度量，学会在同一度量方法下进行不同比较。

片段4：比较面积大小

（1）观察法

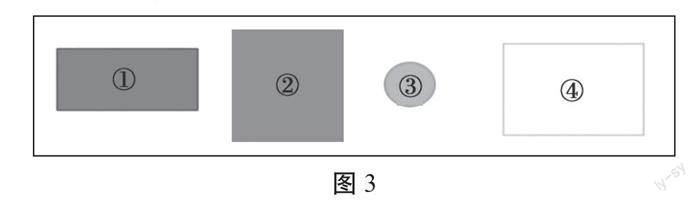
师：你能一眼看出图3中四个平面图形谁的面积最小吗？

生1：③号。

师：你们真会观察！面积相差比较大时，看一看就可以比较。

（2）重叠法

师：谁的面积最大？你们还有什么办法可以比较出来吗？

生2：瞧，把几个图形重叠后就能看出④号最大了。

师：谢谢你，又为我们提供了一种比较面积大小的好方法。

（3）测量法