优质创新试题选登
2023-08-10江贤聪,李晓青,刘娟等
1.2022年2月10日,日本花滑选手羽生结弦在第24届北京冬奥会上挑战4A遗憾失败。4A全称为阿克塞尔四周跳,是花样滑冰所有跳跃动作中难度系数最高的,运动员需要在空中旋转四周半,如图1。如图2,一花滑运动员跳起后离地高度可达0.8 m,落地屈膝的竖直作用距离为0.2 m,作用时间为0.1 s。已知该名运动员的体重是53 kg,重力加速度g取10 m/s2。则落地过程,该名运动员受到地面垂直方向的平均作用力约为其体重的 ( )
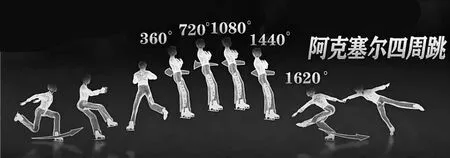
图1

图2
A.2倍 B.3倍 C.5倍 D.7倍
【试题分析】本题与生活紧密联系,主要考查学生模型建构能力。符合四翼中应用性的要求。以运动员的重心作为研究对象,利用自由落体运动规律求得运动员落地瞬间的速度。通过合理假设,落地屈膝可看作匀减速运动求得作用时间,通过动量定理求出这段时间地面对运动员的作用力。
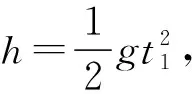
【解析二】由动量守恒定律得Ft-mg(t+t1)=0,解得F=5mg。
【答案】C
(作者姓名、单位:江贤聪 广州市第五中学)
2.2022年春晚舞台上的歌曲《时代感》唱出了对祖国日新月异发展的自豪和对未来的憧憬。在演唱的过程中,演员活力四射、跳出画面的情景给我们留下了很深的印象。如图3,关于演员双脚刚要离开地面的过程中,不计空气阻力,下列说法正确的是 ( )

图3
A.地面对演员的支持力的冲量不为零,做功也不为零
B.演员的机械能守恒
C.演员处于超重状态,且加速度的方向与其动量改变量的方向相同
D.地面对演员的支持力大于演员对地面的压力
【试题分析】试题以春晚舞台上的歌曲《时代感》为试题底色,激发学生热爱祖国的情感、提升他们的民族自信心和自豪感。用演员在表演中跳离地面的过程为情境,考查学生由“实际问题”构建“物理模型”的能力及学生对牛顿运动定律、机械能守恒定律、动量定理、冲量以及功的理解;试题要求学生结合题目信息,考虑演员跳离地面的过程,应用质点模型对本题进行求解。试题突出物理学科的基础性,既注重对核心物理概念和规律的考查,也注重对探究过程、研究方法等内容的考查,试题情境与内容的有机融合,考查学生灵活运用所形成的物理观念、科学思维分析解决实际问题的能力,落实物理学科核心素养的培养。引导学生注重基础,促进课堂回归教材。
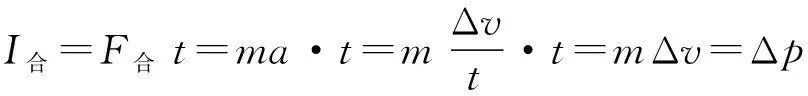
【答案】C
(作者姓名、单位:李晓青 邯郸市第十中学)
3.斯诺克(Snooker)是台球比赛的一种,如图4,5,斯诺克台球有时也被称为障碍台球。此项运动击球次序为一个红球、一个彩球直至红球全部落袋,然后按彩球分值由低至高的顺序也至全部离台为止,最后以得分高者为胜,所有球的重量必须相同。在水平桌面上,对质量为m的白球以速度v0击打一静止的红球的四个全过程进行了频闪照相拍摄,如图所示,据此可推断,在误差范围内,以下说法正确的是 ( )

图4

图5
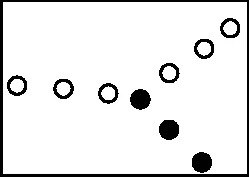
甲
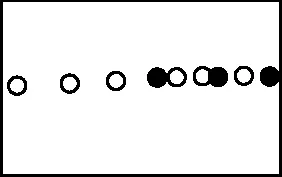
乙
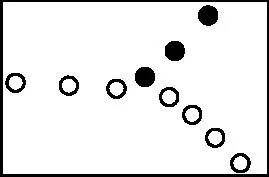
丙

丁
A.甲中系统动量不守恒
B.乙中系统机械能守恒
C.丙中系统损失的动能少于碰撞前总动能的50%
D.丁中对白球而言,碰撞前后受到的冲量大小为2mv0
【试题分析】本题考查动量守恒定律。要求学生基本概念要过关,落实物理观念素养的培养,还需要能将情景与模型相结合,对其科学思维的考查要求较高,还要结合数学估算进行分析与处理,回忆相关的实验情景,对动量相关知识点考查较全面,综合性较强。通过斯诺克台球的引入,将着重分析两个等质量的小球间的碰撞情景。首先需要学生能将生活常见过程与碰撞模型相链接,然后能根据频闪照相的简化图分析碰前碰后两小球的运动情况。
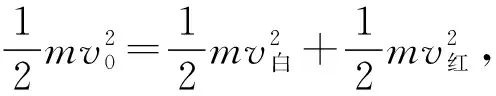
【答案】C
(作者姓名、单位:刘娟 武汉市第十二中学)
4.(多选)2022年2月18日,我国选手谷爱凌在女子U形场地技巧决赛中赢得冠军。决赛中某时刻,谷爱凌从A点冲出场地,此时速度大小为v=12.5 m/s,与竖直方向夹角为θ=37°。在竖直平面运动后落到B点,同时完成左转900°动作,如图6。设C点为最高点,运动员质量为52 kg,重力加速度g=10 m/s2,忽略空气阻力。下列说法正确的是 ( )
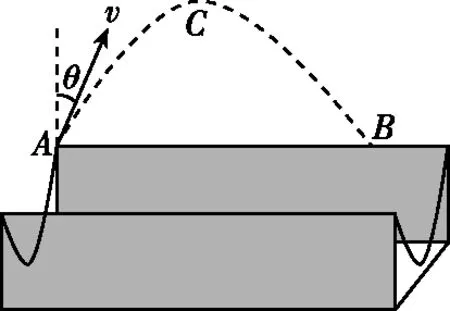
图6
A.最高点C至A的竖直高度为5 m
B.若运动的同时自身做匀速圆周运动,则空中左转的角速度为2π rad/s
C.A点至B点的距离为15 m
D.从A点至C点重力势能增加了2 500 J
【试题分析】根据U形场地技巧决赛实际情境,观察运动中的物理规律。飞出场地后做斜抛运动,同时左转900°做匀速圆周运动,类似于地球的自转。通过计算斜抛运动的竖直高度,让学生对这种运动的高度有所了解,体会比赛的不易。计算左转的角速度,让学生体会是否感到晕眩。计算水平距离,有助于估算U形场地的长度。考查重力势能的计算,体会到能量的转化。竖直方向根据自由落体运动规律求得高度及运动总时间,水平方向根据匀速直线运动规律求得水平距离。由角速度的定义式可求得角速度大小。最后根据重力做负功,可求得重力势能的增加量。
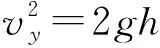
【答案】AC
(作者姓名、单位:刘永阳 陕西省旬邑县中学)
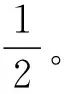

图7
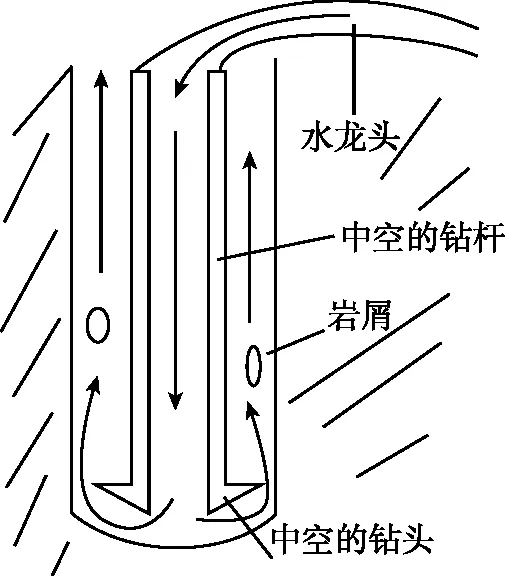
图8
解:流体在与岩石相互作用时,由于其动量发生变化,产生与岩石的相互作用力。
设在一段时间t内,有钻井液喷射的体积为
V=Qt
喷射钻井液的质量为m=ρV
钻井液的动量变化大小Δp=mv1+mv2
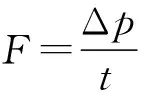
联立解得F=660 N
(作者姓名、单位:郭明林 大理白族自治州民族中学)
6.2022年2月15日,在第24届冬奥会男子单板滑雪大跳台决赛中,中国选手苏翊鸣获得金牌,成为我国历史上最年轻的冬奥冠军。图9为示意图,赛道由出发区(PA段)、助滑区(AB段)、起跳台(CD段)、着陆坡(EM段)、终点区(MN段)五部分组成。假设出发区PA与平面FE的落差h1=48 m,平面FE与终点区MN的落差为h2=36 m,水平滑道BC长度L=36 m,助滑区与着陆坡均为倾斜的坡面,且坡面倾角均为37°,起跳台为一圆弧面,其左端C点与助滑区的底端B点在同一水平面上,圆弧所对应的圆的半径为20 m,圆心角为37°。设在某一次训练中,运动员由A点静止出发,经起跳台起跳后,腾空高度(重心距D点的竖直高度差)为Δh=8 m,最后落在着陆坡上,且落点离坡底M点的距离为30 m,设运动员与滑板的总质量为50 kg,运动员在比赛中可近似地看作质点,且经过赛道的各个连接处时不考虑能量损失,滑板与赛道AB、BC间的动摩擦因数相同,滑板与起跳台CD间摩擦力不计,不计空气阻力,取g=10 m/s2。(sin37°=0.6,cos37°=0.8)求:
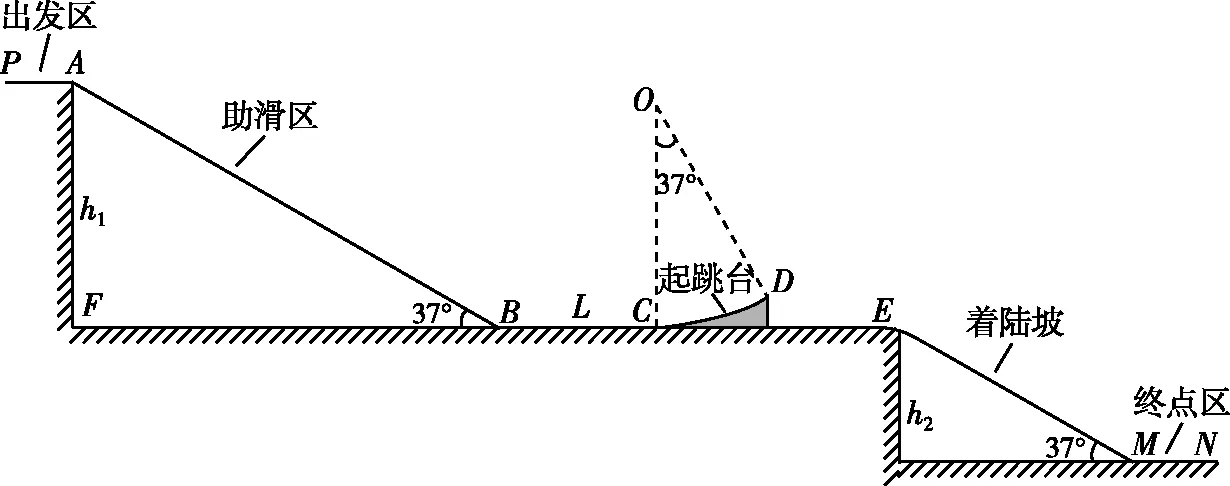
图9
(1)运动员在离开起跳台右端D点的速度大小;
(2)运动员在经过起跳台左端C点时对赛道的压力大小;
(3)滑板与赛道AB、BC间的动摩擦因数;
(4)运动员在空中能用于完成动作的时间。
解:(1)从D点到最高点,可看作逆向平抛运动,且vD与水平方向夹角为37°,设D点的竖直分速度为vy。
由平抛运动可得
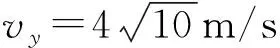
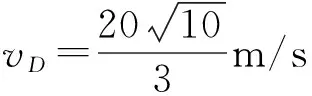
(2)由C到D根据机械能守恒得
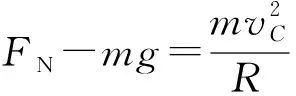
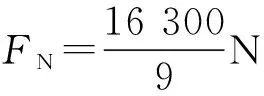
由牛顿第三定律可知,对赛道的压力
(3)由A到C根据动能定理得
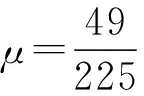
(4)运动员从D点上升至最高点所用的时间
从最高点下落至着落坡时,由图10可知,总的落差为H=30 m
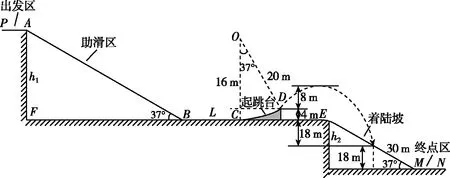
图10

