风机锚杆松弛对基础局压混凝土疲劳损伤的影响分析

伍 军,刘哲锋,楚加翼,向 康,李鹏飞

(长沙理工大学土木工程学院,湖南长沙 410114)

随着化石能源逐渐枯竭,气候危机不断加剧,发展风电已成为重要的研究课题,其被作为达到“双碳”环保目标、实现可持续发展的重要措施[1]。2022年中国陆上风电新增装机容量48 GW,所有吊装的陆上风电机组中,3.0 MW及以上占比高达74.1%[2-3],中国风电正迈向大风机时代。大多风机采用锚杆连接塔筒与基础,锚固区混凝土局压效应突出[4]。与此同时,风机锚杆松弛问题日益严峻,极易造成基础局压混凝土疲劳损伤破坏。因此,探究锚杆松弛状态下基础局压混凝土的损伤演化规律十分必要。

现阶段,国内外学者针对锚杆式风机基础的损伤问题做了部分研究。韩彦宝等[5]以某风电场为例,从锚杆数量、锚杆到承台中心的距离、基础底板半径等方面进行了计算分析,探讨了风电场岩石锚杆基础设计中存在的问题;周建华等[6]通过开展锚杆试件应力松弛试验和风机基础锚杆预应力监测,获得了表征锚杆长期运行特性的预应力及预应力保留百分比与时间的函数关系,并指出锚杆松弛大致分2个阶段,其中第1阶段损失快且持续时间短;黄冬平等[7]从基础环和预应力锚栓的受力原理出发,依照国标计算应力幅,说明预应力锚杆抗疲劳的相对优势;申海洋等[8]建模探究预应力锚杆对风机混凝土基础抗裂和抗腐蚀的作用,强调预拉力作用能充分激发混凝土的受压性能,减缓受拉开裂和渗水腐蚀;王尔贝等[9]建模研究锚杆数量与直径改变对基础承载特性的影响,发现承载力随锚杆数量变多先增后减,而随锚杆直径加大线性提高;DE GROOT等[10]建模分析锚栓笼对混凝土的约束作用,结合试验数据发现,虽然锚栓笼的预应力能加强混凝土受压,但应力集中也可能导致软弱混凝土提前压坏;WANG等[11]对某风机基础中突然断裂的2根预应力高强钢筋进行多次测试,并仿真模拟断裂过程,证实断裂原因为氢辅助裂化和高应力集中的共同诱导;刘嫔等[12]对风机基础锚固区混凝土的局部压应力、局部受压区的截面尺寸和局部受压承载力进行了验算分析,为预应力锚杆基础的设计提供了参考。

以上研究多是凸显风机锚杆在风机基础整体受力中的优势和对锚杆失效的溯源分析,类似锚杆松弛的局压混凝土损伤破坏分析相对匮乏。因此本文结合内蒙古某锚杆式风机基础工程,通过对锚杆设置不同程度的预应力损失来模拟松弛发育过程,研究锚杆松弛加剧过程中局压混凝土的疲劳损伤规律,并对风机基础的安全设计与日常运维提出建议,以供同类工程参考。

1 有限元数值模拟

1.1 风机基础结构及材料参数

以内蒙古某3.0 MW风机为研究对象,该风机轮毂高90 m,基础采用钢筋混凝土圆形重力式扩展基础型式,依据NB/T 10311—2019《陆上风电场工程风电机组基础设计规范》[13],设计级别为甲级,下卧土岩组合地基,建筑场地类别划分为Ⅱ类。基础几何尺寸如图1所示,底板半径为9.3 m,高为1 m,台柱半径为3.2 m,高为1.1 m,高强灌浆料厚90 mm,锚板厚80 mm,锚杆分布外半径为2.3 m,内半径为2.2 m,基础埋深3.5 m(从自然地面起算)。

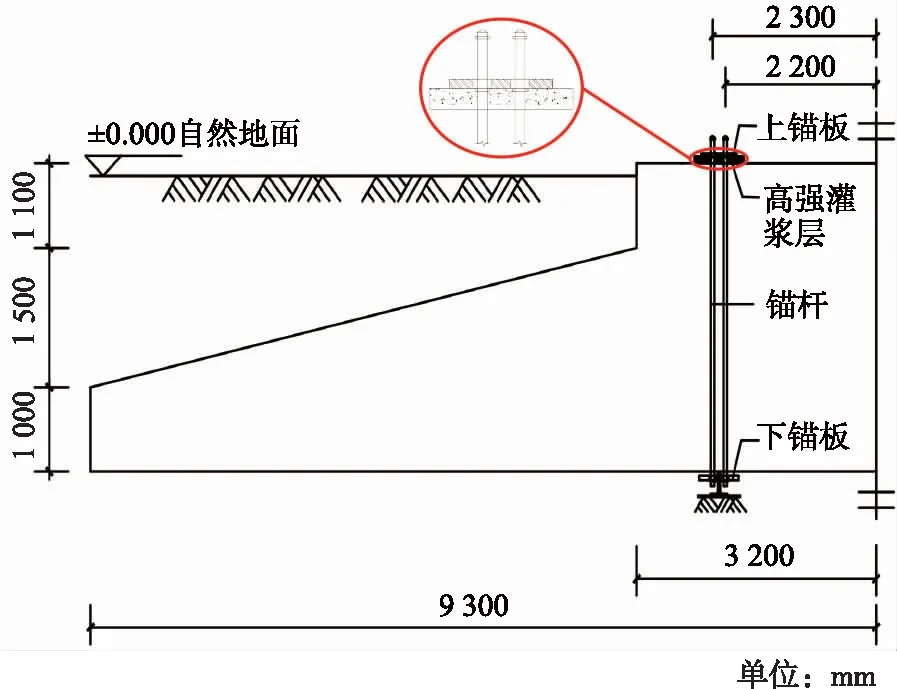
图1 风机基础剖面Fig.1 Wind turbine foundation profile

根据该风机基础《设计计算总说明》和《工程地质勘察报告》,基础混凝土级别为C40;高强灌浆料采取C80;垫层采用C10;钢筋级别为HRB400;锚板为Q345E钢材;所有锚杆为M42,8.8级;160根分内外2圈均匀布置。风机基础物理力学参数详见表1[14],地基土物理力学参数详见表2[15]。

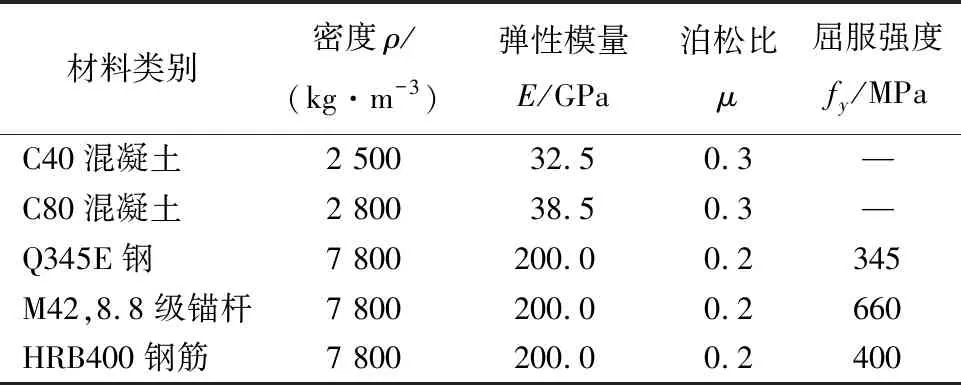
表1 风机基础物理力学参数

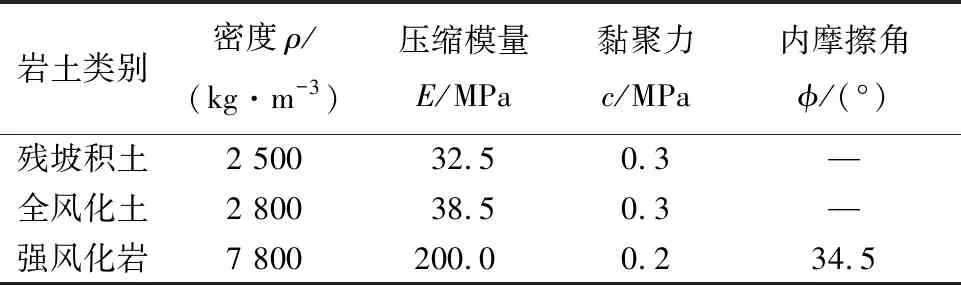
表2 地基土物理力学参数

地基土从上至下可简化为残坡积土、全风化土及强风化岩3个土层,持力层为强风化岩。土层简化及其物理力学参数如表2所示。

1.2 ABAQUS有限元模型

利用ABAQUS有限元软件[16]建立带土柔性基础,土体采取圆柱体建模将基础包裹,水平延伸和纵向深度方向边界均取5倍基础直径,并赋予CIN3D8无限元边界[17],与有限元无缝衔接,相互补充,考虑土体无界性,滤去有限边界波的反射对结构响应的影响。为降低建模繁琐程度,将锚杆简化为钢筋线单元,两端吻合于锚板上表面中心施以MPC约束,类型为beam,初始预应力为500 kN,采用降温法施加,定义风机基础材料的温度线膨胀系数为1 × 10-5。现今风机锚杆多采取无粘结锚固的施工方式,因而在模型中沿锚杆与混凝土共节点设置刚性弹簧限制径向偏移,仅允许纵向收缩。钢筋均采用T3D2桁架单元,嵌入于基础,其他部件均采用C3D8R实体单元,锚板与混凝土、垫层与土体之间材料不同,采用摩擦接触,设置为有限滑移,切向采用库仑摩擦接触,摩擦系数为 0.35,法向接触作用为硬接触。相同性质材料之间紧密结合,可视为不存在相对滑动,故采取绑定约束,协调受力变形。整体模型如图2所示,共计划分106 589个单元,其中中心小圆圈显示的就是模型中锚杆与周围混凝土共节点设置的刚性弹簧。

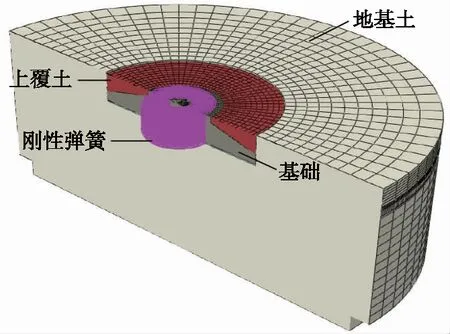
图2 风机基础有限元模型Fig.2 Wind turbine foundation finite element modeling

混凝土材料本构采用CDP塑性损伤模型,考虑刚度退化和塑性损伤累积等材料性能劣化全过程,计算参考GB 50010—2010《混凝土结构设计规范》(2015年版)[15]附录C中混凝土受压、受拉应力-应变公式进行,其本构曲线如图3所示。而钢材通常不易屈服,采取线弹性本构便于计算。土体遵循摩尔-库仑破坏准则,应用简单,又能充分反映土体的剪切特性,模型材料参数取值见表1和表2。

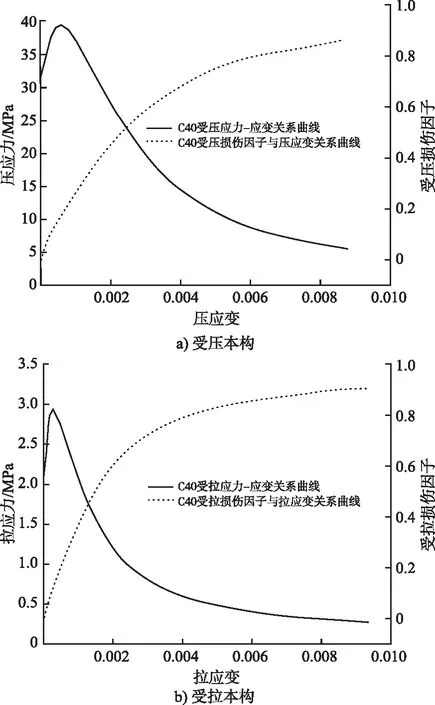
图3 C40混凝土的应力-应变曲线及损伤因子应变曲线Fig.3 Stress-strain and damage factor strain curves of C40 concrete

由于风机基础通常在主风向上受循环作用后产生疲劳损伤,因此本文仅计算疲劳荷载工况,参照该风机基础《设计计算总说明》,主要的荷载信息汇总如表3所示。通过在基础顶面设置参考点集中施加荷载,参考点与上锚板顶面分布耦合约束。

表3 荷载工况

1.3 锚杆松弛计算工况

由于风机对风向敏感,在风机运行期间,迎风侧锚杆长期受拉,一旦松弛将致基础严重损伤,因此按最不利原则假设主风向迎风侧α角度内锚杆松弛。考虑到实际工程中可能存在着小范围松弛辐射在年检中未及时排查,本文定义α为18°,再扩大范围基础将不能正常受力,研究意义不大。锚杆松弛区域见图4。

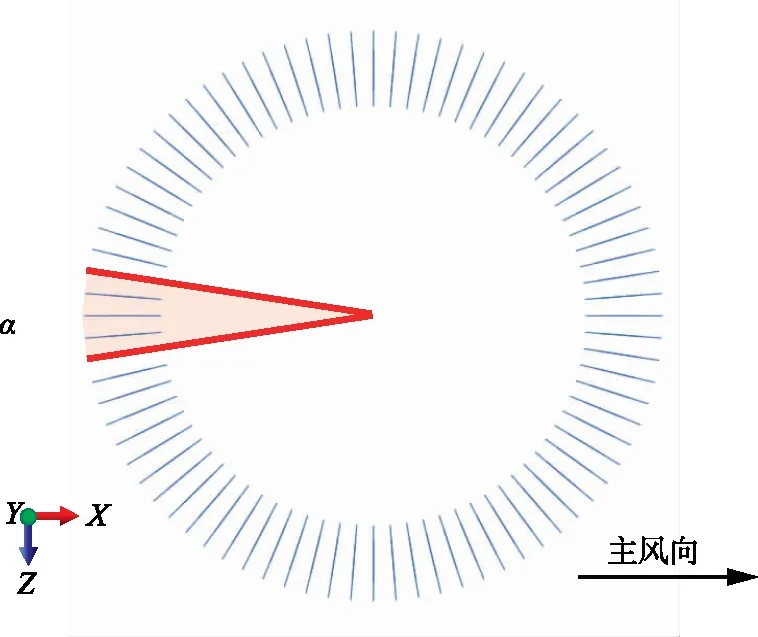
图4 锚杆松弛区域Fig.4 Anchor relaxation area

锚固区混凝土局压作用较大,本文主要分析锚固区局压混凝土的压应力分布变化,并在背风侧混凝土与上锚板接触位置找到最大压应力点,将其定义为局压混凝土热点,进一步开展局压混凝土热点的疲劳验算,示意图如图5所示。

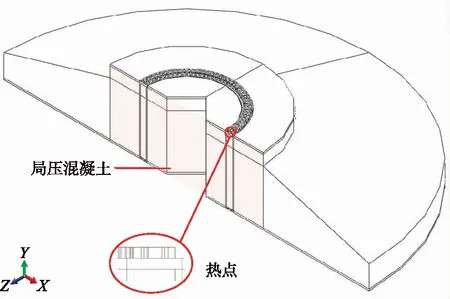
图5 局压混凝土及热点示意Fig.5 Partial pressure concrete and hot spot schematic

针对锚杆松弛的发展趋势问题,宋洋等[18]已建立起描述外力作用下的锚杆预应力损失模型,明确指出初始预应力为500 kN时,锚杆的预应力损失率最高可达20%,因此本文对松弛锚杆等比设置4%,8%,12%,16%和20%的预应力损失,并应用温降法公式换算成相应的温度场施加,共计6种松弛工况,详见表4。

表4 α角度区域锚杆松弛计算工况

2 计算结果分析

2.1 局压混凝土疲劳计算方法

风机结构对应20 a使用寿命的等效循环次数为1×107,采用GB 50010—2010《混凝土结构设计规范》(2015年版)[15]给出的计算方法不符要求,德国劳埃德船级社(germanischer lloyd,GL)认证的“Guideline for the certification of wind turbines”(2010)[19]推荐采用CEB-FIP Model Code[20]对结构进行疲劳分析,可针对不同等效循环次数要求进行疲劳验算,因此本文参照该规范对局压混凝土热点进行疲劳强度分析。混凝土疲劳抗压强度按式(1)、式(2)计算:

fcd,fat=0.85βcc(t)[fck(1-fck/25fck0)]/γc,fat,

(1)

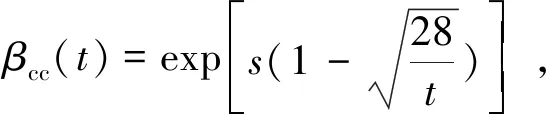
(2)

式中:fcd,fat为混凝土疲劳抗压强度;βcc(t)为混凝土强度系数;fck为混凝土静力强度;fck0为参考静力强度;γc,fat为疲劳工况混凝土材料分项系数;s为水泥强度系数;t为混凝土的龄期。

混凝土应力幅通过式(3)、式(4)计算,再根据式(5)—式(7)计算混凝土疲劳强度对应的疲劳寿命。 当lgN1≤6时,取lgN=lgN1;当lgN2>8时,取lgN=lgN2。最终若lgN>7,那么说明风力机基础能承受1×107以上循环次数的疲劳荷载作用,满足规范要求。表达式如式(3)—式(7)所示:

ΔScd=Scd,max-Scd,min,

(4)

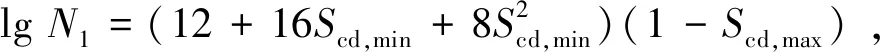
(5)

lgN2=0.2lgN1(lgN1-1) ,

(6)

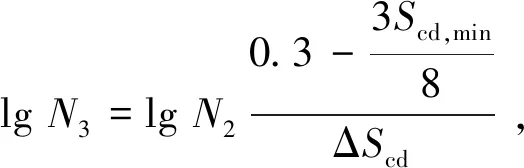
(7)

式中:γEd为荷载分项系数;ηc为混凝土压应力不均匀系数;Scd,max,Scd,min为最大及最小压应力水平设计值;ΔScd为设计疲劳应力幅;N1,N2,N3为循环次数;σc,min,σc,max为疲劳谷值和峰值下混凝土最大压应力。

2.2 局压混凝土疲劳分析

有限元计算结果显示基础底板的压应力变化在0.1 MPa以内,锚杆松弛对基础底板受压效应微乎其微,可忽略不计,而对锚固区局压混凝土的受压效应及分布影响较大,因此本研究就图5所示的局压混凝土展开疲劳分析。

在疲劳荷载谷值作用下,锚杆发生松弛后局压混凝土压应力的数值分析结果如图6所示。局压混凝土全截面受压,背风侧局部应力较大,为应力薄弱位置,最大压应力均出现在主风向背风侧局压混凝土与上锚板的接触部位,受风荷载方向性和锚杆松弛的双重影响所致。通过对比图6 a)—f)可以发现,随着锚杆松弛不断加剧,局压混凝土热点应力从11.32 MPa增大至13.91 MPa,增幅为22.87%,始终小于C40混凝土疲劳抗压强度设计值16.89 MPa,仍具有较大的安全储备。此外,从图6可以看出,局压混凝土区域逐渐从迎风侧向背风侧转移,锚杆松弛后局压混凝土背风侧应力集中益发明显,任由发展必将导致该部位混凝土压碎开裂,须及时对松弛锚杆复加预紧力,并对混凝土开裂部位予以灌浆加固。

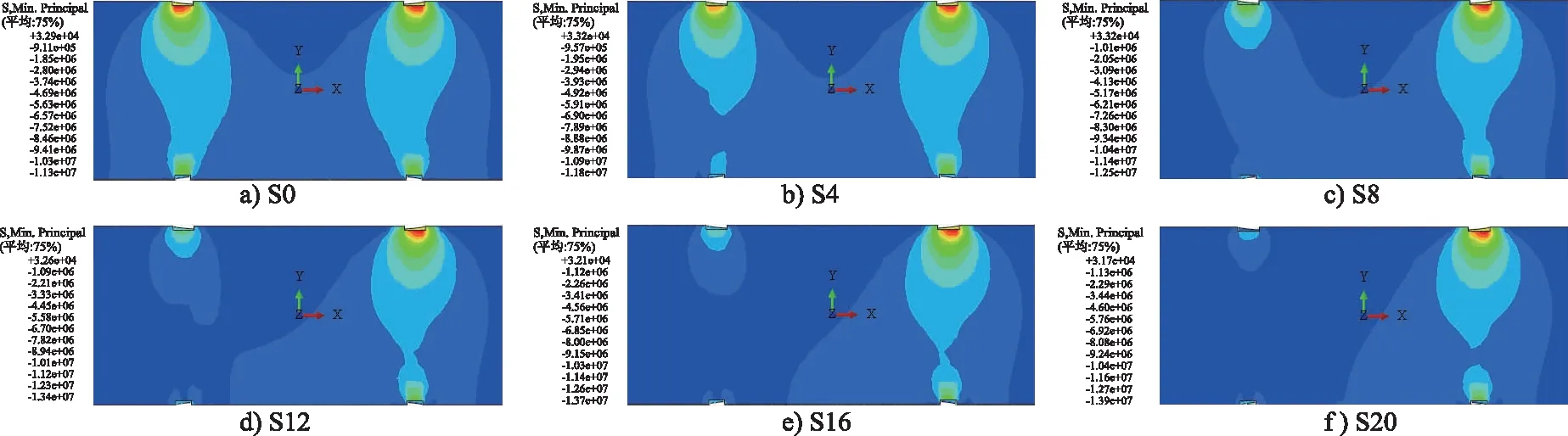
图6 疲劳谷值作用下局压混凝土压应力分布Fig.6 Distribution of compressive stress in partial pressure concrete under the action of fatigue valley

图7为疲劳峰值作用下锚杆松弛后局压混凝土的压应力分布云图。与疲劳谷值的计算结果相比,局压混凝土的受压效应整体上显著加大,且从迎风侧向背风侧转移的速度也更快。对比图7 a)—f)可以发现,局压混凝土热点应力从12.15 MPa增大至23.36 MPa,增长了11.21 MPa,增幅高达92.26%,且S12工况下为19.13 MPa,超过C40混凝土疲劳抗压强度设计值16.89 MPa,不再满足规范要求。S20工况下混凝土受压区域集中于背风侧,迎风侧混凝土退出受压,转为受拉,拉应力最大为0.733 MPa,小于混凝土抗拉强度设计值,说明混凝土在锚杆发生松弛时并不会发生受拉破坏,破坏形式仍以局压破坏为主,须重点关注局压混凝土受力情况。

通过对局压混凝土在疲劳荷载谷值和峰值下的受压应力分析可以发现,局压混凝土的受压应力水平在锚杆发生松弛后均有不同程度的上升,局压混凝土热点应力集中现象愈发严峻。结合以上数值计算结果,应用第2.1节中所述的混凝土疲劳理论计算方法对局压混凝土热点的受压循环次数(疲劳寿命)进行评估,计算流程及结果汇总如表5所示。

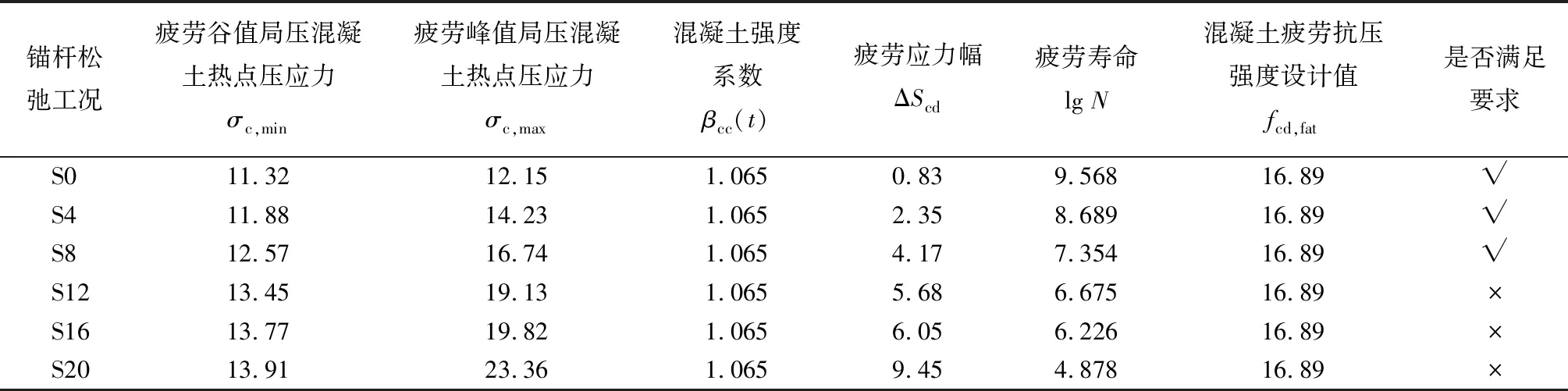
表5 局压混凝土热点疲劳计算结果

由表5可见,当锚杆松弛加剧,局压混凝土热点的疲劳应力幅逐渐加大,松弛8%时已十分接近混凝土疲劳抗压强度设计值,而疲劳寿命随即不断减小,风机结构的期望寿命为1×107次,局压混凝土热点疲劳寿命在锚杆松弛达12%时低于期望值。综合混凝土疲劳抗压强度设计值和疲劳寿命2项指标,锚杆松弛达到12%后,局压混凝土的疲劳性能不再满足要求。

3 结 语

本文以内蒙古某3.0 MW锚杆预应力风机基础工程为研究背景,通过在ABAQUS软件中调整预应力锚杆的温度场来模拟锚杆松弛过程中不同阶段,对疲劳荷载工况下不同锚杆松弛比例时基础局压混凝土应力分布变化进行分析,并对局压混凝土热点开展了疲劳寿命验算,研究锚杆松弛发展过程中基础局压混凝土的损伤演化规律,得出如下主要结论。

1)锚杆松弛会对局压混凝土的受力分布造成影响。随着锚杆松弛加剧,混凝土受压区域会从迎风侧向背风侧转移,迎风侧混凝土将退出受压,转为受拉工作,背风侧混凝土应力集中愈加突出。因此可重点关注背风侧混凝土的受力情况,以此作为锚杆发生松弛的判断依据。

2)通过局压混凝土热点的疲劳强度分析和疲劳寿命评估发现,当锚杆松弛达到8%时,背风侧混凝土极有可能发生局压破坏;当锚杆松弛达到12%,背风侧混凝土已低于疲劳寿命预期,极有可能发生疲劳破坏,须及时对松弛锚杆复加预紧力,限制锚杆松弛进一步发展。综合评判后可将锚杆松弛8%视为威胁基础安全的红线。

本文结合锚杆松弛频发和混凝土局压易碎的问题,采取数值模拟的方法对二者之间的潜在规律做了挖掘。研究成果虽对同类工程具有一定的指导意义,但研究过程中对荷载做了简化,且仍局限于静力分析。考虑到实际风机运行过程中以动力受荷为主,后续可到现场做周期性监测试验或提取SCADA荷载监测数据,整理形成可靠的荷载时程输入模型,以更好地模拟真实的风机受荷情形,使计算结果更具说服力。此外,本研究仅着重分析锚杆松弛对基础局压混凝土疲劳性能的影响,忽略了疲劳循环次数对锚杆松弛的影响,下一步研究可将该因素考虑在内。