长圆形孔的结构参数对其周边应力的集中影响
2023-08-09彭培英刘庆刚孙占朋
曹 凯,彭培英,刘庆刚,孙占朋
(河北科技大学机械工程学院,河北石家庄 050018)
在过程工业中,越来越多的长圆形开孔结构应用在压力容器筒体上,随之带来补强计算、应力分析、安全评定等方面的问题[1]。凸缘是圆筒形容器长圆形孔补强的首选结构,但各国标准并未对长圆形开孔凸缘补强方法做出详细规定[2],因此针对长圆形孔凸缘补强结构的研究越来越受到关注。目前,长圆形开孔补强设计主要采用以下2种方法:一是“常规设计”方法,此方法仅仅局限于“当在壳体上开椭圆形或长圆形孔时,孔的长径与短径之比不大于2.0”的条件,工程上许多情况都不能适用;二是采用“应力分析设计”方法,设计人员需要首先假定开孔补强结构参数,然后采用力学理论计算、实验测试或可靠的数值方法对结构进行应力分析,并根据分析结果判断其强度是否满足要求,此方法过程复杂,需要反复试算,不利于采用程序化软件提高设计效率[3-4]。从以上2种设计方法出发,研究人员开展了一系列关于圆筒形容器长圆形孔应力分析和补强研究。随着计算机技术的发展,有限元方法在开孔结构应力分析问题中的应用越来越广泛[5-7],黄明松等[8]结合工程实际认为有限元分析软件能够很好地解决设备大开孔的应力分析和强度计算,通过有限元分析法可以得到较为可靠的应力结果;陈庭清[9]介绍了制药行业中使用有限元分析软件对压力容器上长圆形开孔进行局部有限元分析的案例,验证了关于ASME规范中有关长圆形开孔时短半径方向应进行适当加强的观点;桑如苞等[10-16]针对圆筒形容器上开长圆形孔,从工程设计角度出发提出一种近似计算方法,当开孔尺寸与圆筒直径相比较小时,将其作为二维应力状态下的大平板开椭圆形孔问题进行处理,又基于受力平衡,研究了筒体大开孔计算和分析中环向弯矩的来源,并且考虑了管道附加载荷对压力容器应力分析的影响;随着理论研究的深入,面对各种复杂情况与多因素影响,利用数值模拟、正交试验和极差分析,通过改变模型参数、控制变量等方式可以获得更为准确的结果[17-18]。综上所述,当前研究未对影响长圆形孔应力的因素开展具体分析,结构参数的设计要求也未明确说明,系统的补强设计方法较少。
本文采用数值模拟、理论分析和实验测试相结合的方法,针对不同的长圆形孔结构参数,分析开孔周边应力分布情况,研究结构参数对最大应力集中系数的影响,对明确此类结构的补强设计方法、提高设计效率及保障其安全性具有明显的意义。
1 几何模型
图1为长圆形孔凸缘补强结构示意图。影响长圆形孔凸缘补强结构的主要结构参数包括:筒体直径(D)、短轴与筒体直径之比(b/D)、长短轴之比(a/b)、凸缘宽度(B)和凸缘高度(H)。
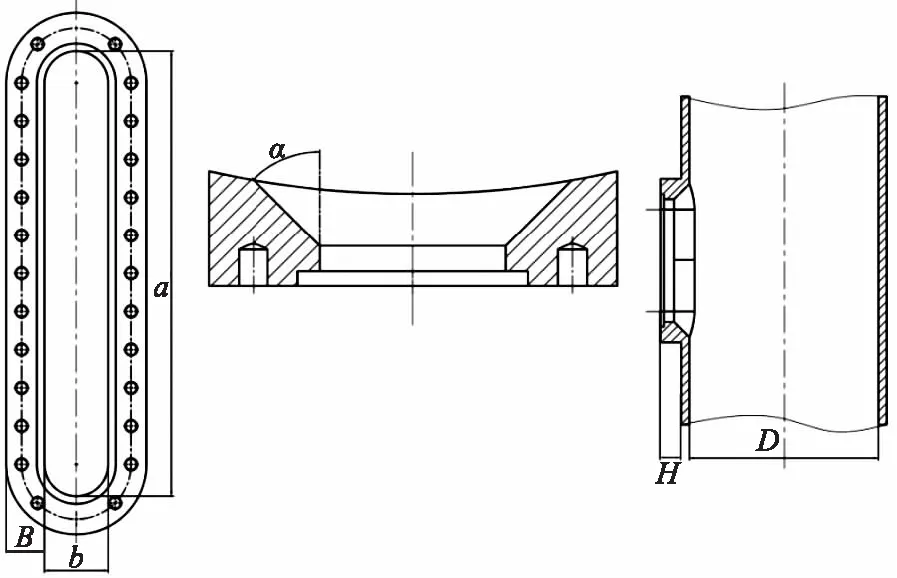
图1 长圆形孔凸缘补强结构示意图Fig.1 Schematic diagram of structural of oblong opening with the reinforcement flange
根据工业生产中长圆形孔的常用几何尺寸,本文中D的取值为300~4 000 mm;为了消除筒体支撑情况等对长圆形孔周边应力分布的影响,筒体的长度取值大于直径的3倍;b/D取值小于0.3,a/b取值为1~5,长轴(a)小于0.5倍的筒体长度,开角α取45°,筒体厚度t按GB 150—2011《压力容器》[3]的要求计算得到。
2 有限元模型的建立与验证
2.1 材料参数
根据压力容器分析设计标准规定,采用弹性应力进行结构的安全评定,因此本文采用线弹性本构模型。采用承压设备最常用的Q345R材料进行分析,其相关性能参数如表1所示。

表1 Q345R材料性能参数
2.2 网格划分
采用ANSYS Workbench软件进行数值模拟,利用Mesh工具对模型整体进行网格划分,单元类型为solid186。为提高计算精度,对长圆形孔边半径2b范围内球形区域进行网格局部细化,如图2所示。

图2 网格模型Fig.2 Grid model
根据网格独立性原则对网格的尺寸及数量进行分析,按照第三强度理论确定的最大等效应力值确定网格的数量,具体见表2。
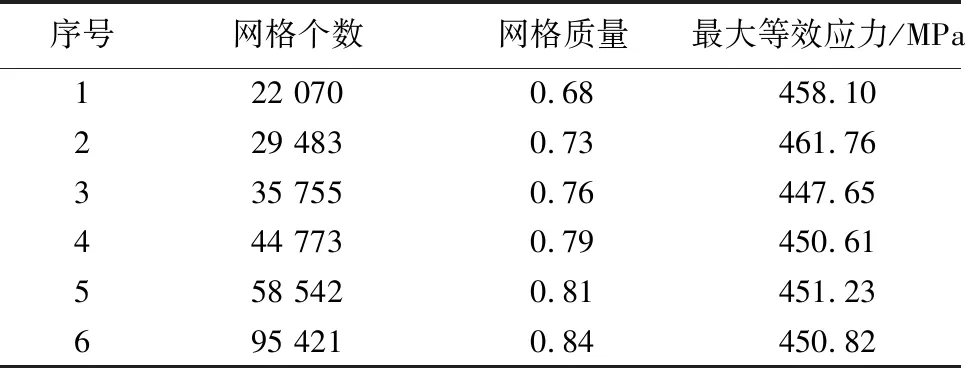
表2 不同网格划分下的最大等效应力
由表2可知,当网格个数大于44 773时,最大等效应力值趋向于稳定,并且网格质量在0.75以上,数值模拟结果较为可靠,因此本文选用网格个数为44 773时对应的单元进行数值模拟。
2.3 边界条件
在筒体一端面施加固定约束,另一端面施加等效轴向拉力,所有对称面上施加无摩擦支撑;对筒体和长圆形孔内表面施加内压,其载荷及边界条件如图3所示。
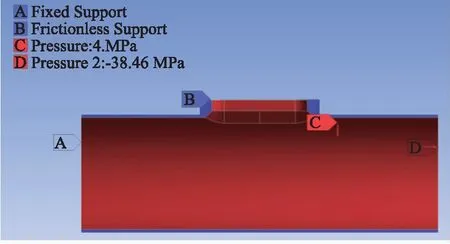
图3 简体和长圆形孔内表面的载荷及边界条件Fig.3 Loads and boundary conditions on inner surface of cylinder and oblong opening
2.4 模型验证
为了验证数值模拟的可靠性,对于D=1 000 mm,b/D=0.2,a/b=2,B=90 mm,H=90 mm的模型,在内压p=4 MPa条件下,进行了数值模拟,并采用电阻应变法测定了如图4所示的路径L上的环向应力(σθ)。路径L的起点位于筒体外表面长轴端点,沿筒体轴线方向朝着远离开孔方向延伸。实验测试与数值模拟的结果对比如图5所示。
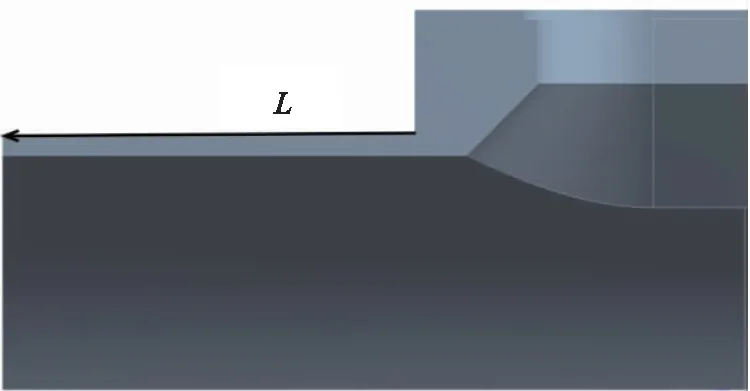
图4 应力测试实验路径Fig.4 Path used in experimental stress tests
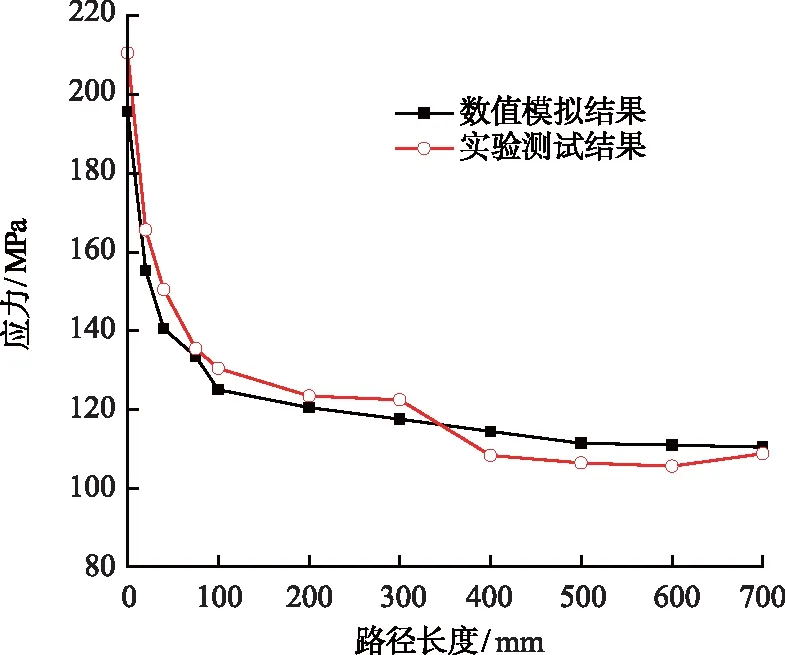
图5 实验测试结果与数值模拟结果对比Fig.5 Comparison between experimental test results and numerical simulation results
由图5可知,数值模拟结果与实验测试结果较为吻合,最大误差不超过10%,表明数值模拟结果较为可靠。
3 长圆形孔周边应力分布规律
3.1 长圆形孔周边应力分布情况
压力容器分析设计标准中,采用应力强度(stress intensity)参数来进行安全评定。应力强度(σsi)是指按照第三强度理论计算得到的等效弹性应力,具体计算方法如式(1)所示。
σsi=σ1-σ3,
(1)
式中:σ1和σ3分别表示第一主应力和第三主应力,MPa。
对于D=1 000 mm,b/D=0.2,a/b=2,B=90 mm,H=90 mm的模型,在内压p=4 MPa条件下,长轴和短轴端点附近σsi的分布如图6所示。
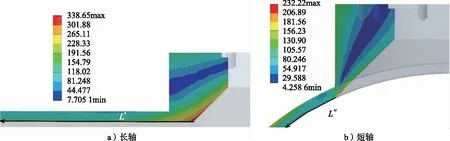
图6 长轴与短轴端点附近区域应力分布Fig.6 Stress distributions near the ends of long axis and short axis
由图6可知,开孔附近区域内表面应力强度明显大于外表面应力强度,长轴端点附近区域应力强度明显大于短轴端点附近区域应力强度。为了定量分析长轴和短轴端点附近应力强度,分别建立了如图6所示的路径L′和L″,其中路径L′从长轴端点内表面开始,沿筒体轴向朝着远离开孔部位方向延伸;L″始于长圆孔中间部位短轴端点内表面,沿着筒体环向朝着远离开孔部位方向延伸。路径L′和L″上的σsi随路径长度的变化如图7所示。
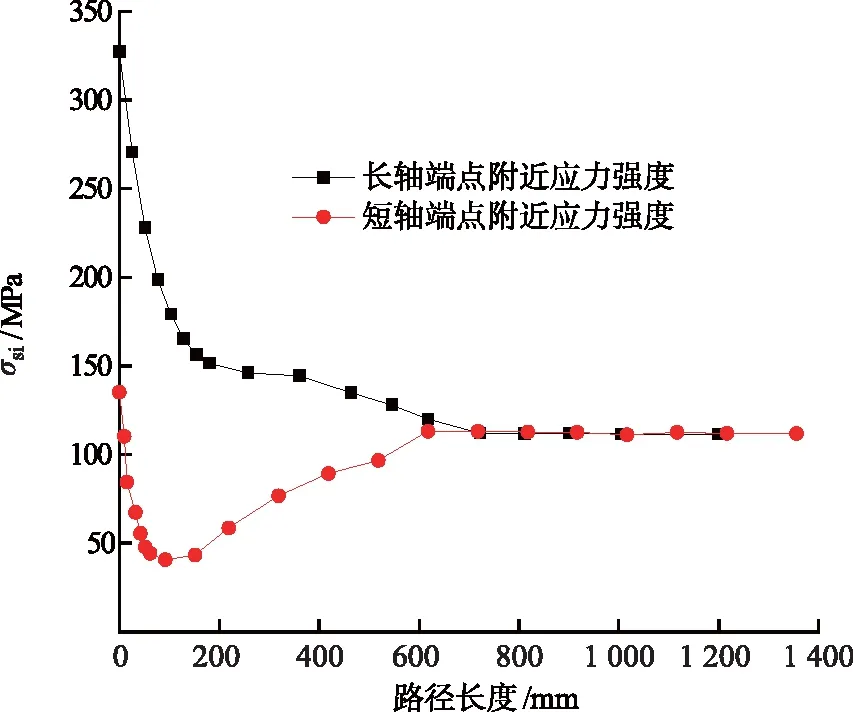
图7 长轴与短轴端点附近路径L′和L″的应力强度Fig.7 Stresses intensities near the ends of long axis and short axis paths
由图7可知,长轴端点的σsi的最大值达到338.65 MPa,且随着离开长轴端点距离的增加而迅速下降,最终稳定于110 MPa左右;短轴端点的应力强度最大值为232.22 MPa,随着离开短轴端点距离的增加呈现先降低后增加趋势,最终也稳定于110 MPa左右。分析结果表明,开孔区域存在明显的应力集中,且长轴端点附近区域的应力强度数值明显大于短轴。因此,本文主要针对长轴端点附近区域的应力集中情况进行分析。
3.2 长轴端点附近应力集中系数
为了定量研究长圆形孔周边的应力集中情况,在筒体内表面长圆形孔长轴端点处沿着筒体轴线方向设置一条路径L1,如图8所示。采用路径上的点到长轴端点的距离(x)与长圆形孔短轴(b)之比f来表征应力集中的影响范围,如式(2)所示。
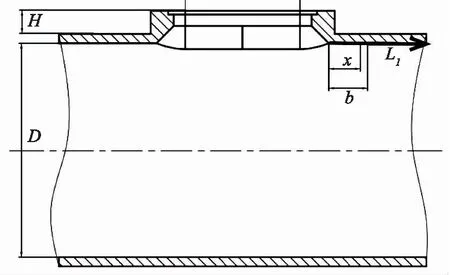
图8 长圆形孔长轴端点附近路径示意图Fig.8 Schematic diagram of path from the end of long axis of oblong opening
f=x/b。
(2)
工程上一般采用应力集中系数来表示孔边应力集中的程度。在压力容器分析设计方法中,圆筒形容器的应力集中系数(K)指容器应力集中部位的应力强度最大值(σmax)与远离应力集中部位的筒体应力强度(σeq)的比值[19],如式(3)所示。
K=σmax/σeq,
(3)
式中:σeq=σθ-σr,σθ为筒体环向薄膜应力,MPa;σr表示筒体的径向应力,MPa;σθ和σr按照式(4)确定。
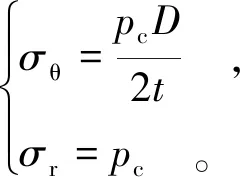
(4)
在筒体结构不连续区域(如开孔),受边缘力、边缘力矩、内压的共同影响,存在较大应力集中。不同结构参数条件下的长圆形孔周边应力集中系数如图9所示。
由图9可知,随着离开长圆形孔长轴边缘的距离不断增加,K迅速下降,然后逐渐趋向一个稳定的数值。当离开长轴边缘的距离超过1.5b时,K几乎不再发生变化,且趋向于1,其应力强度也逐渐接近σeq。这表明长圆形孔应力集中主要分布在1.5b范围内,当超出长圆形孔周边1.5b范围时,长圆形开孔几乎对筒体强度没有影响。
4 参数对最大应力集中系数的影响
4.1 筒体直径的影响
由于D在一定程度上影响筒体壁厚,在其他参数不变的情况下,D越大,筒体壁厚越大,筒体整体强度越大,直接影响最大应力集中系数(Kmax)的大小,因此需要分析不同条件下长圆形孔长轴端点的Kmax随D的变化情况,结果如图10所示。
由图10可知,Kmax随着D的增加而缓慢增加,D对Kmax的影响较小。其中,图10 a)表示b/D分别为0.1,0.2,0.3时Kmax随D的变化情况,D相同时,b/D越大,Kmax越大,b/D对Kmax的影响较为明显;图10 b)表示a/b分别为2/1,3/1,4/1时Kmax随D的变化情况,D相同条件下,a/b越大,Kmax越大,a/b对Kmax的影响也较为显著;图10 c)表示B分别为4t,6t,8t时Kmax随D的变化情况,3条曲线较为接近表示B对Kmax的影响不太显著;图10 d)表示H分别为4t,6t,8t时Kmax随D的变化情况,H=6t和H=8t的2条曲线较为接近,但距离H=4t的曲线较远,表示当H较小时,其对Kmax的影响较为明显,随着H的增加,其影响逐渐降低。
4.2 短轴与筒体直径之比的影响
由于b/D在一定程度上决定筒体开孔大小,在其他参数不变的情况下,b/D越大,开孔越大,筒体整体强度的削弱程度越大,直接影响Kmax的大小,因此需要分析不同条件下长圆形孔长轴端点的Kmax随b/D的变化情况,结果如图11所示。
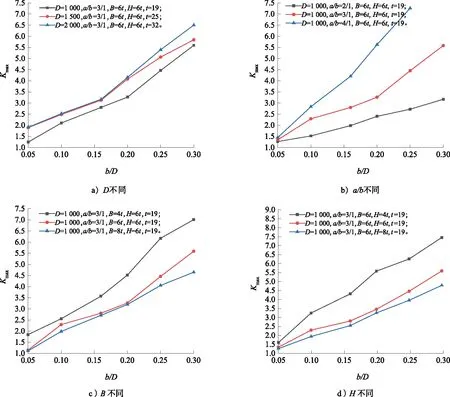
图11 短轴与筒体直径之比对最大应力集中系数的影响Fig.11 Effects of ratio of short axis and barreldiameter on maximum stress concentration factor
由图11可知,b/D对长圆形孔的Kmax影响较为显著。b/D值越大,Kmax也越大;随着b/D的增加,Kmax呈线性上升趋势。
图11 a)表示D分别为1 000,1 500,2 000 mm时Kmax随b/D的变化情况,D=1 500 mm和D=2 000 mm的曲线较为接近,但距离D=1 000 mm的曲线较远,表明随着D的增加,D对Kmax的影响逐渐减弱;图11 b)表示a/b分别为2/1,3/1,4/1时Kmax随b/D的变化情况,当b/D较小时,a/b的影响并不显著,但随着b/D的增加,a/b的影响程度也迅速增加。图11 c)表示B分别为4t,6t,8t时Kmax随b/D的变化情况,图11 d)表示H分别为4t,6t,8t时Kmax随b/D的变化情况。由图11 c)—图11 d)可知,Kmax随B或H的增加而降低,但降低速度逐渐减缓。
4.3 长短轴之比的影响
由于长圆形孔的a/b直接决定开孔大小,a/b越大,开孔越大,筒体整体承压面积越小,直接影响Kmax的大小,因此需要分析不同条件下长圆形孔长轴端点的Kmax随a/b的变化情况,结果如图12所示。
由图12可知,a/b对长圆形孔的Kmax影响显著,a/b值越大,Kmax也越大,并且随着a/b的增加Kmax呈线性增加。
图12 a)表示D分别为1 000,1 500,2 000 mm时Kmax随a/b的变化情况,3条曲线十分接近,表示D对于Kmax的影响并不显著。图12 b)表示b/D分别为0.05,0.10,0.15时Kmax随a/b的变化情况。图12 c)表示B分别为4t,6t,8t时Kmax随a/b的变化情况。图12 d)表示H分别为4t,6t,8t时Kmax随a/b的变化情况,可以看出,当a/b较小时,b/D,B和H对Kmax的影响很小,但随着a/b的增加,其影响程度也逐渐增加。
4.4 凸缘宽度的影响
由于长圆形孔的B在一定程度上影响筒体整体的承压面积,B越大,承压面积越大,筒体整体强度越大,直接影响Kmax的大小,因此需要分析不同条件下长圆形孔长轴端点的Kmax随B的变化情况,结果如图13所示。
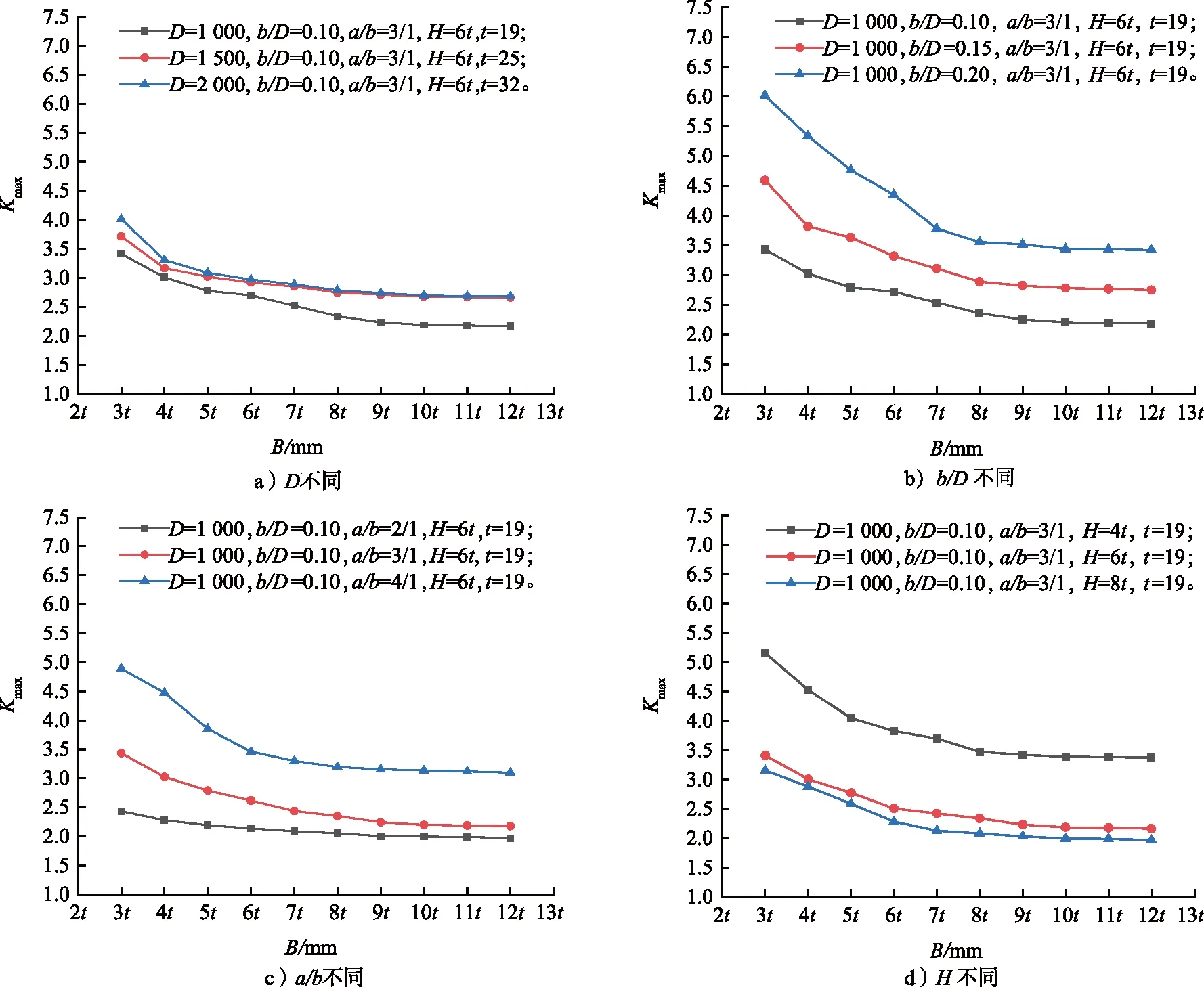
图13 凸缘宽度对最大应力集中系数的影响Fig.13 Effects of flange width on maximum stress concentration factor
由图13可知,B对Kmax的影响较小,随着B的增加,Kmax缓慢变小;当B超过一定数值后,Kmax不再继续变小,表明当B达到一定数值时,持续增加B对于提高开孔补强效果并不理想。
图13 a)表示D分别为1 000,1 500,2 000 mm时Kmax随B的变化情况,由图可知,D对Kmax的影响并不明显。图13 b)表示b/D分别为0.10,0.15,0.20时Kmax随B的变化情况,图13 c)表示a/b分别为2/1,3/1,4/1时Kmax随B的变化情况,图13 d)表示H分别为4t,6t,8t时Kmax随B的变化情况。由图13 b)—图13 d)可知,Kmax随a/b和b/D的增加而增加,随H的增加而降低,但降低程度逐渐减缓。
4.5 凸缘高度的影响
增加长圆形孔的H相当于增加了开孔边缘的筒体厚度,对开孔造成筒体强度的削弱有一定的补强作用。长圆孔长轴端点的Kmax随H的变化情况,如图14所示。
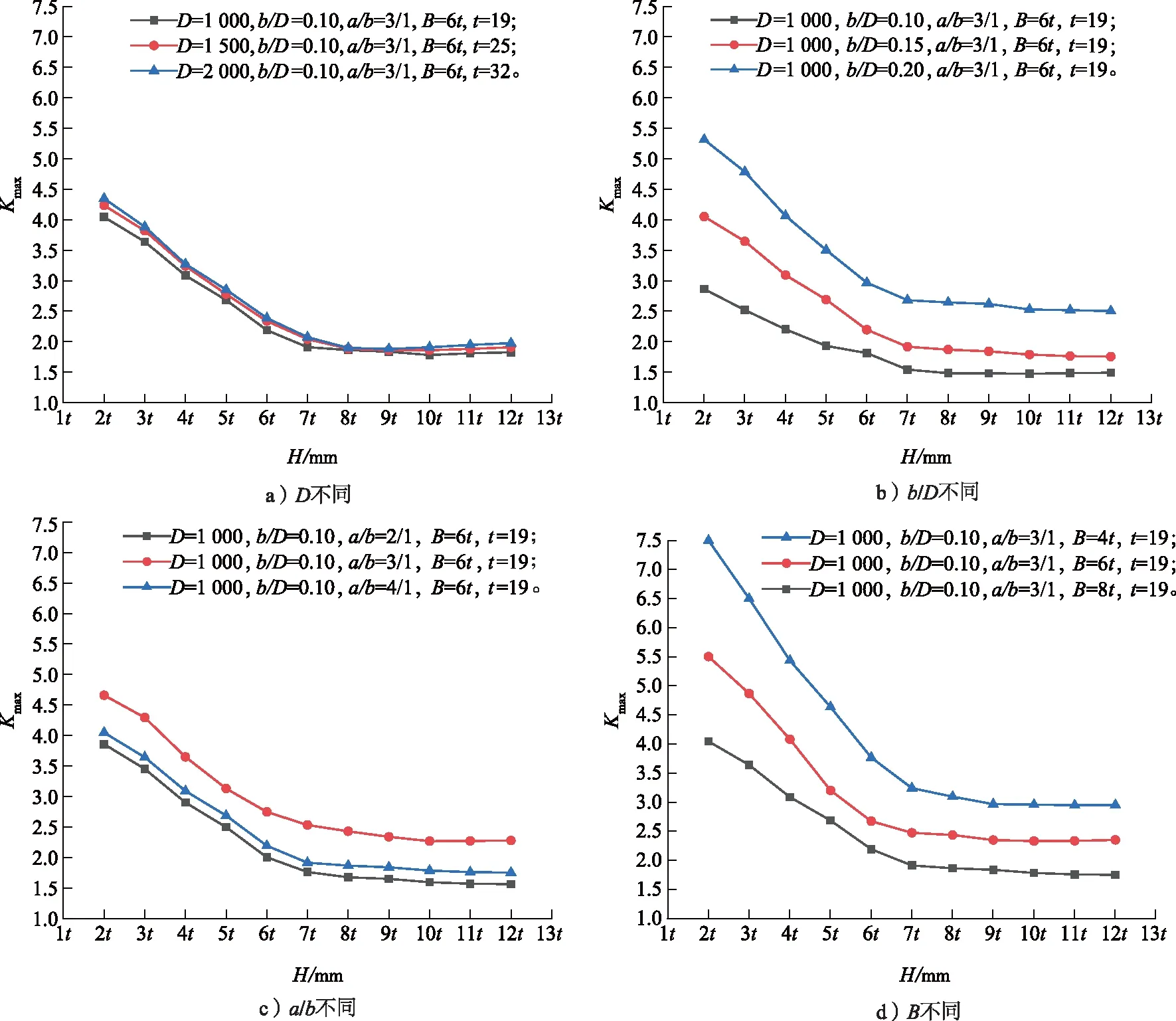
图14 凸缘高度对最大应力集中系数的影响Fig.14 Effects of flange height on maximum stress concentration factor
根据图14可知,H对长圆形孔的Kmax影响较为显著,随着H的增加,Kmax变小,并且在一定范围内呈线性变化;但当H到达一定极限时,进一步增加H对降低Kmax的帮助不大,持续增加H并不是提高补强效果的有效方法。
图14 a)表示D分别为1 000,1 500,2 000 mm时Kmax随H的变化情况,由图可知,D对Kmax的影响不大。图14 b)表示b/D分别为0.10,0.15,0.20时Kmax随H的变化情况,图14 c)表示筒体a/b分别为2/1,3/1,4/1时Kmax随H的变化情况,图14 d)所示为B分别为4t,6t,8t时Kmax随H的变化情况,由图14 b)—图14 d)可知,随着b/D和a/b的增加,Kmax均呈现增加趋势,随着B的增加,Kmax呈现降低趋势。
4.6 结构参数显著性分析
为了进一步明确长圆形孔的5个结构参数对其Kmax的影响显著程度,本文采用极差分析方法[20]对结构参数的影响显著程度进行分析。根据长圆形孔的5个结构参数,设计5因素5水平的全因素全水平试验,因素水平如表3所示。
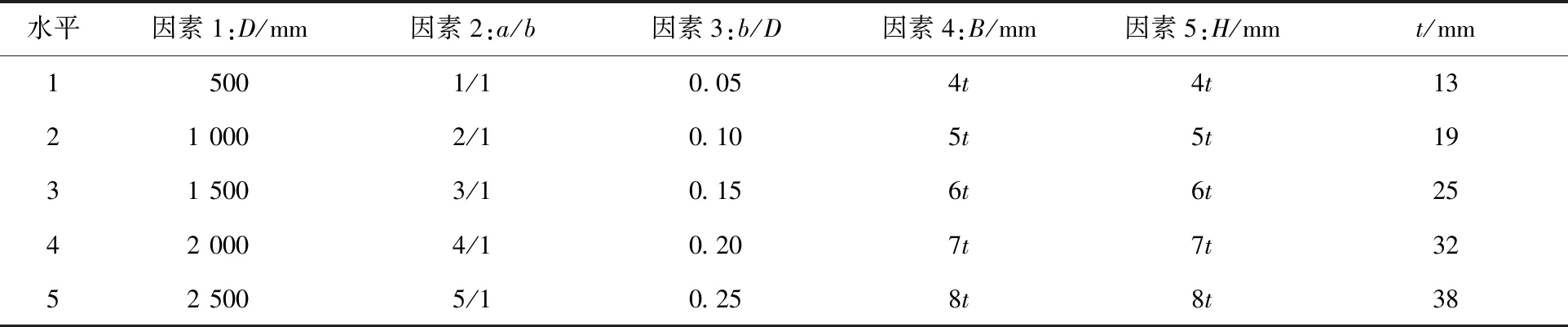
表3 长圆形孔基本因素水平表
根据表3,设计了25个数值模拟试验,得到不同条件下长圆形孔长轴端点的Kmax,具体模拟方案及结果如表4所示。
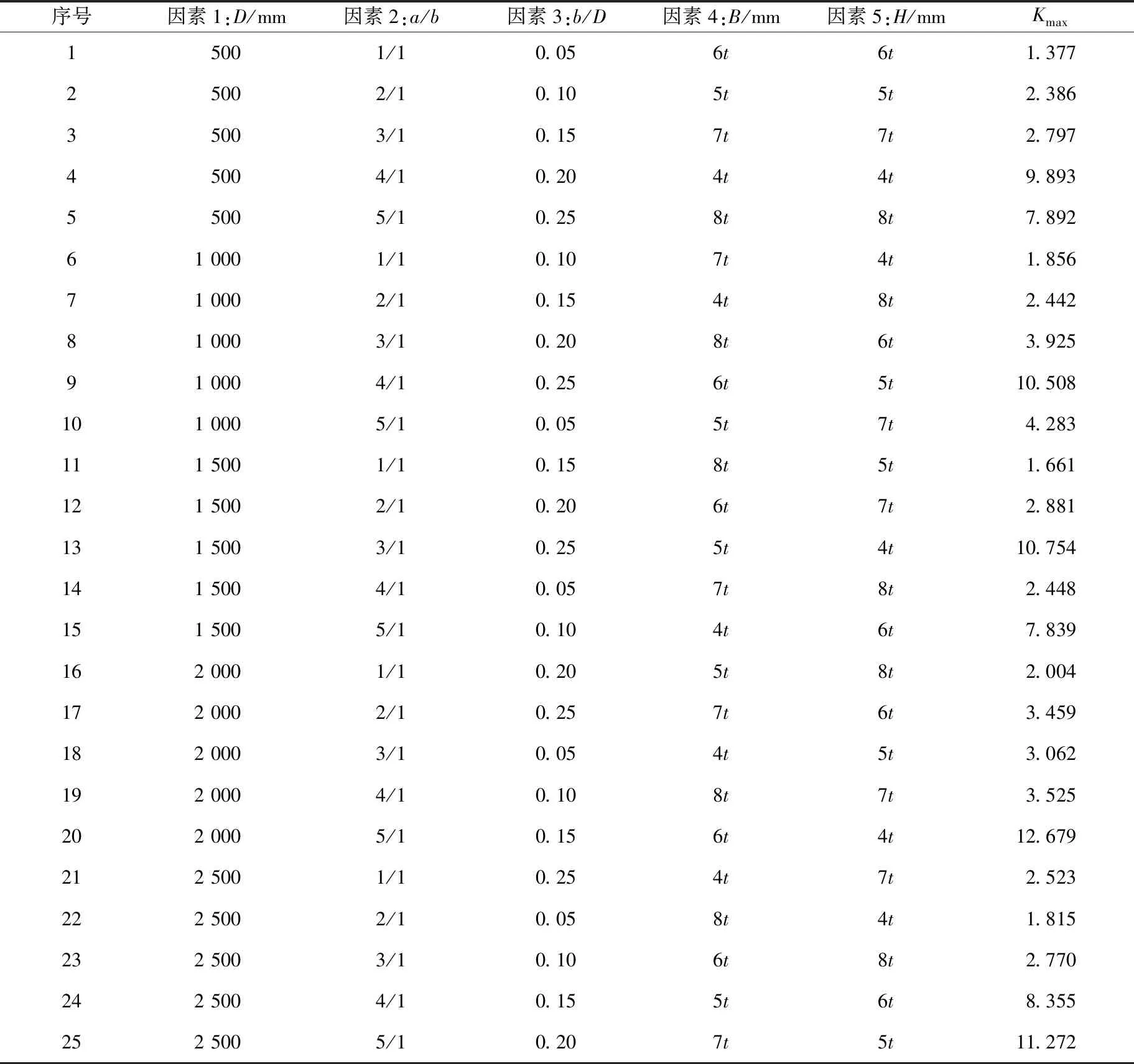
表4 长圆形孔因素正交试验表
对正交试验结果进行极差分析,极差分析结果如表5所示。
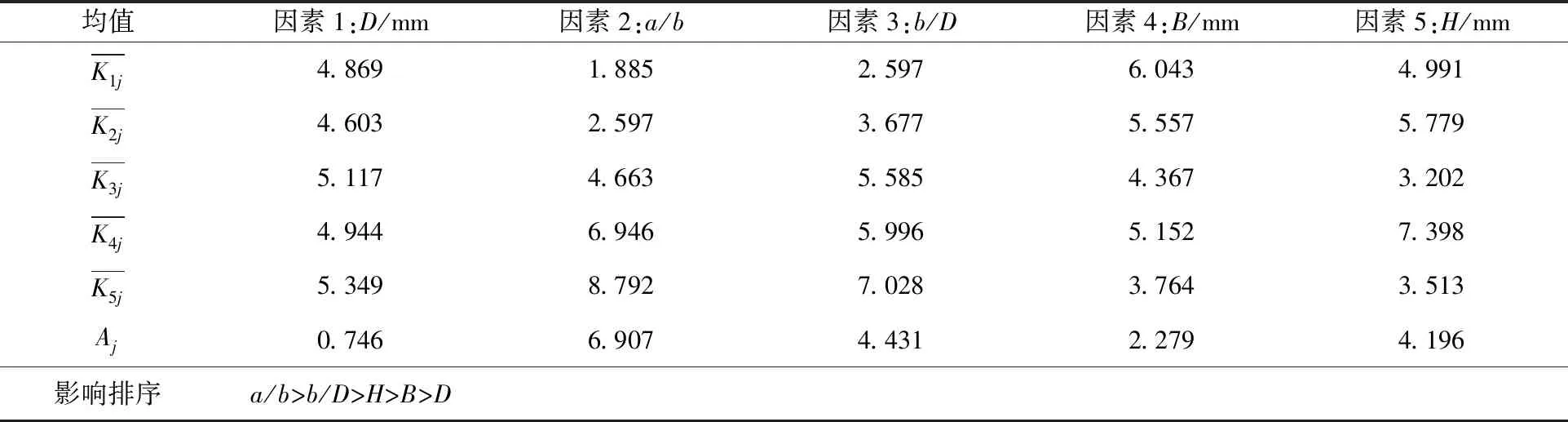
表5 长圆形孔结构参数极差分析结果
由表5可知,各参数对Kmax的影响程度排序:长短轴之比(a/b)>短轴与筒体直径之比(b/D)>凸缘高度(H)>凸缘宽度(B)>筒体直径(D)。其中:a/b对Kmax的影响程度最高;b/D和H对Kmax的影响程度相当,但明显低于a/b;B和D对Kmax的影响程度最低。
5 结 语
本文采用数值模拟、理论分析和实验测试相结合的方法,采用ANASYS Workbench软件对圆筒形容器不同结构参数的长圆形孔补强结构设计进行了应力分析,主要结论如下。
1)影响长圆形孔周边应力集中情况的主要参数有5个,分别为筒体直径(D)、短轴与筒体直径之比(b/D)、长短轴之比(a/b)、凸缘宽度(B)和凸缘高度(H)。
2)长圆形孔周边应力呈对称分布,最大应力位于长轴两端内表面处,且随着到长轴端点距离的增加而迅速降低,应力集中情况主要出现在距离长轴端点1.5b范围内。
3)最大应力集中系数(Kmax)随着a/b,b/D的增加而增加,随B和H的增加而降低,但当B和H超过一定范围时,K不再随其增加而降低。
4)5个参数中,a/b对Kmax的影响程度最高,b/D和H对Kmax的影响程度相当,但明显低于a/b,B和D对Kmax的影响程度最低。
本文主要针对开孔的结构参数对应力集中的影响进行了定性分析,未来研究工作的核心会集中于得到长圆形孔周边应力集中系数与开孔几何尺寸的数学关联式,以实现长圆形孔补强设计的程序化。
