新型沙丘形突扩燃烧室三维冷态背风角度研究*

李 凯，曾卓雄，徐义华

(1南昌航空大学飞行器工程学院，南昌 330063;2上海电力学院能源与机械工程学院，上海 200090)

0 引言

当前燃烧室设计面临的新挑战是如何进一步提高燃烧室性能和减少排气污染等［1］。为了使燃烧室内燃烧能稳定进行，人们通常利用各种方式生成回流区，常规突扩燃烧室就是其中一种。它的工作原理是:突扩扩张的几何形状使气流分离，分离流在压力梯度作用下回流到火焰根部连续点火，从而使火焰稳定［2］。但常规突扩燃烧室存在火焰稳定性差［3-5］、燃烧效率低等缺点。常出现于沙漠的沙丘引起的流场具有较好的稳定性和较小的阻力，文中由此提出一种新型的突扩燃烧室——沙丘形突扩燃烧室，即在突扩口前后面引入迎风角度和背风角度［6］。在突扩燃烧室中，回流区的大小和位置、回流量的多少都直接影响燃烧过程、燃烧效率和火焰的稳定性，因此研究突扩燃烧室内气体流动的规律具有实际意义。文中对不同背风角度的沙丘形突扩燃烧室冷态流场进行数值模拟，分析不同情况下的回流区流动特性，比较各种情况的总压损失系数，从而为实际设计提供理论依据。

1 计算几何模型和控制方程

由于沙丘形突扩燃烧室为三维轴对称管道，所以采用中心对称截面来标示计算模型的具体尺寸(如图2)。其中外径D=2R=120 mm，内径d=2r=80 mm，突扩高度 h=20 mm，前迎风角度［7］α =10°，突扩比 E=D/d=3/2［8］，燃烧室尺寸足够长，不低于 10 h，分别对背风角度β=30°～90°的流场进行数值模拟。

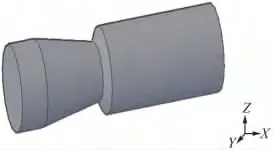
图1 沙丘形突扩燃烧室模型

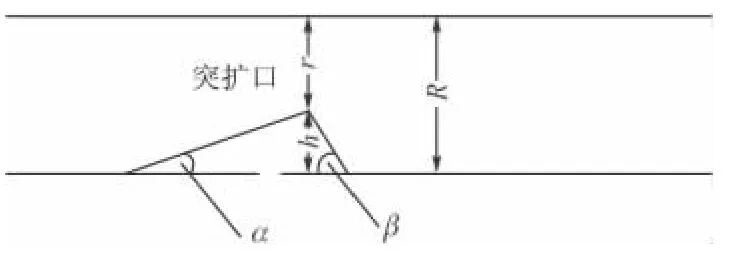
图2 中心对称截面

湍流模型采用Realizable k-ε模型，选择标准壁面函数(standard wall function)。扩散项采用中心差分格式，对流项采用二阶迎风格式。来流条件采用速度入口边界条件，来流速度V=40 m/s;出口采用压力出口边界条件，出口压力定为大气压(101 325 Pa)。计算结果与网格数量无关。所求解的定常控制方程组包括质量连续方程、动量方程、湍流动能方程、湍流耗散率方程，其中通用形式为［9］:

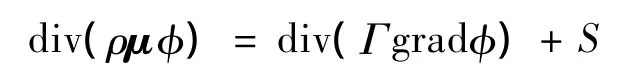
2 数值模拟结果与分析

2.1 算例验证

对具有实验数据的中心突扩燃烧室流动［10］进行了数值模拟，得到回流区最大负速度绝对值u1与入口速度u的关系，如图3所示。从图中可知，计算结果与实验值差异很小，从而表明文中所用的数值模拟计算方法是可信的。

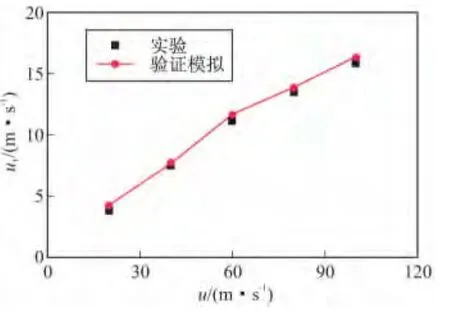
图3 计算结果对比

2.2 总压损失分析

定义出口总压损失系数δ为:

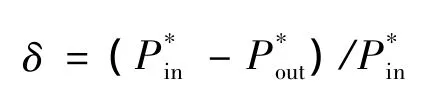
由图4可知，燃烧室总压损失系数随背风角度的增大而增加。在80°前总压损失增加缓慢，从80°到90°，总压损失系数有一个明显的阶跃上升趋势，这是因为90°时突扩为台阶状，没有一个渐变扩张的过程，从而加大了主流突扩引起的总压损失。在30°时，总压损失系数最小为1%，由于背风角度小，趋向于水平平面，渐变扩张趋势明显，避免了高速主流突扩产生的较大的总压损失。总的来说，背风角度在30°至80°之间，总压损失系数范围为1% ～1.22%，变化范围不大，且都满足整体燃烧系统总压损失系数小于6%［11］的期望。

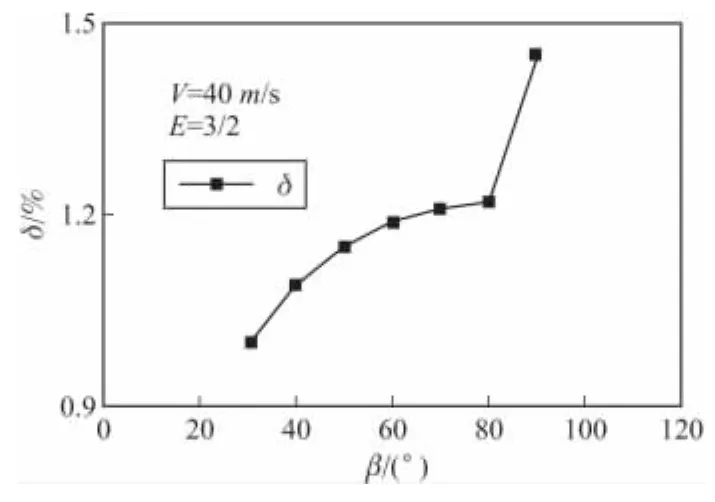
图4 燃烧室总压损失系数

2.3 平均静压分析

静压是影响火焰传播速度的一个重要参数。当压力下降时，着火敏感期τ将增加［12］。着火敏感期τ的增加对发动机燃烧室的启动没有好处，所以期望突扩段下游能有一个较高的静压值。在文中计算中，沿燃烧器x轴向任意截面的平均静压Pavg［13］定义为:

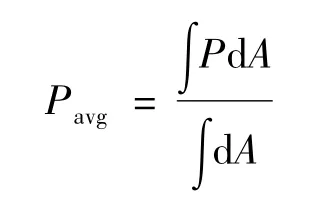
其中:P为扩压器内任一点处的静压值，A为该点所处的横截面面积。

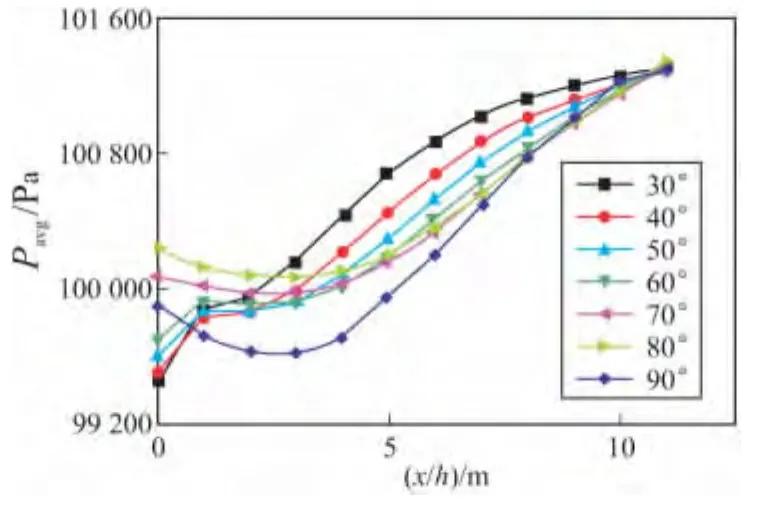
图5 截面平均静压变化

图5为不同背风角度下平均静压沿x轴向的变化趋势。从图中可以看出，背风角为30°到60°时，平均静压Pavg的变化趋势相似，即沿x轴方向在突扩口截面(x/h=0)后到1倍突扩高度(x/h=1)前，平均静压Pavg有一个快速上升过程，随后小幅上升一段距离后又较快上升，最后增长速度又趋于平缓;背风角度为70°到90°时，平均静压Pavg的变化趋势也相似，即沿x轴方向在突扩口截面(x/h=0)后到3倍突扩高度(x/h=3)前，平均静压Pavg有一个下降的过程，随后平均静压快速上升，最后也开始减慢增长速度。在出口截面处，不同背风角度的平均静压Pavg都接近于同一个值，这是因为流动充分发展，流通通道主要由主流占据，来流速度相同，且总压损失相差不大，所以静压互相接近。从图中可以看出，背风角为30°时，沿x轴方向3～10倍h距离上，其静压最大，40°时次之。但背风角为40°时相对其他情况的静压也有一个比较明显的升高。

2.4 流动速度与压力分析

图6、图7分别为燃烧器背风角60°时突扩口下游近壁面的静压和沿x轴方向的速度分布。不同角度下，突扩口下游近壁面的静压和x轴方向速度的分布趋势相互类似。由壁面附近的x轴方向速度分布容易得到突扩回流区的长度，因为再附着点的x轴方向速度为零。由图6可知，突扩回流区的长度约为8.5倍突扩高度。由图7所示，从再附着点到背风坡角，压力先下降，接着恢复，快速下降部分表示气流加速，逆向返流速度增大，对应于等值流线图可以看出，此时流线弯曲的厉害。压力过了最低压力点后又逐渐上升，表示气流开始减速，静压恢复缓慢，因而流线弯曲不大。对比图6和图7可知，最低压力点和最大返流速度点并不重合。从再附着点开始，先达到最大速度点，而压力最低点滞后，这与 Teyssandier［14］的积分分析结果一致。

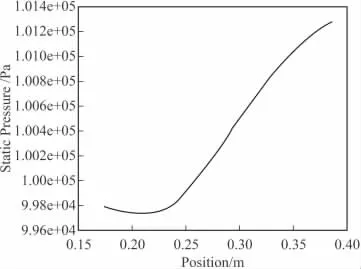
图6 突扩口下游近壁面静压分布

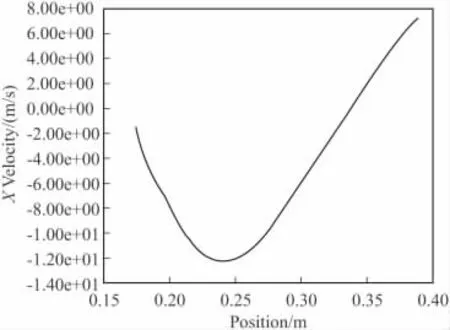
图7 突扩口下游近壁面x方向速度分布

分析不同背风角度下突扩口下游近壁面的x轴方向速度分布，可以得到不同背风角度下突扩回流区的长度以及最大返流速度，具体数值见表1。

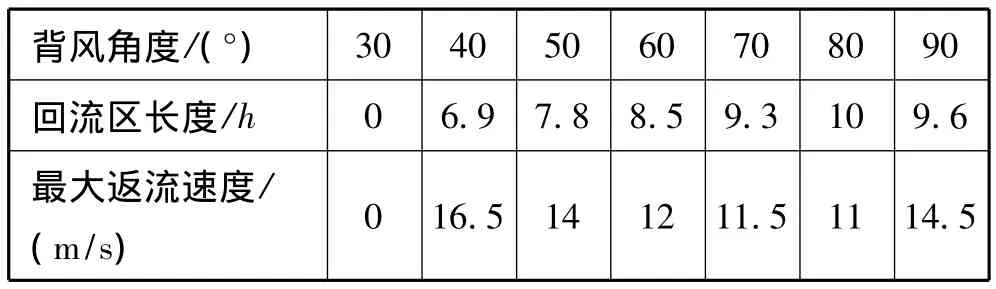
表1 不同背风角度下突扩口下游近壁面突扩回流区长度和最大返流速度

2.5 流场结构分析

由于模拟采用三维模型，为了较为全面了解三维沙丘形突扩燃烧室内的流场，文中选取z=0和y=0两个截平面上的流线分布来分析燃烧室内流场的特征。

图8(a)为背风角度30°下燃烧器z=0和y=0截面的等值流线图。在z=0截面中上下两侧形成一对不对称的旋涡，且下侧旋涡很小。在y=0截平面中只有上侧形成了旋涡，但在下侧没有产生旋涡。没有回流区的产生就不能稳定火焰，形成一个稳定的点火源。

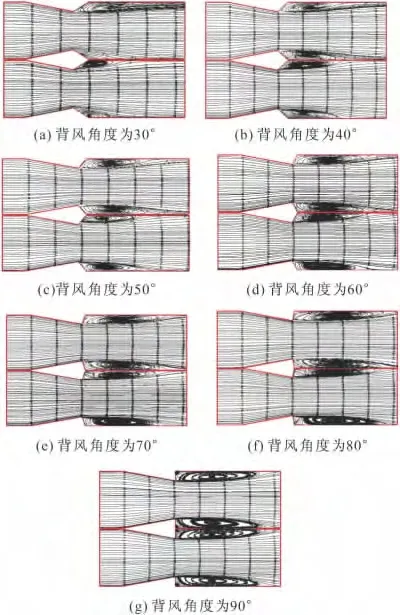
图8 不同背风角度下截平面的等值流线图

图8(b)为背风角度40°下燃烧器z=0和y=0截面的等值流线图。在z=0截面和y=0截面中，上下两侧都形成了较为对称的一对旋涡，并且形成的回流区长度短，面积小，所以回流区总压损失较低，从而出口总压损失也较低。同时均匀的旋涡分布有利于火焰稳定，最大返流速度相比其他情况最大，旋涡强度高，利于燃料和空气的掺混以及传热、传质、燃烧过程的进行。

图8(c)为背风角度50°下燃烧器z=0和y=0截面的等值流线图。在y=0截面中，上下两侧形成了一对对称的旋涡，然而在z=0截面中，上下两侧形成的旋涡并不对称。z=0截面上侧旋涡内侧流线背离涡心，不稳定;外侧流线指向涡心，形成稳定极限环。这种情况体现了三维特性。不对称的旋涡不利于火焰稳定，且其回流区长度比背风角40°情况下有所增加，回流区面积增大，总压损失也增加。这与背风角度为60°至80°条件下流场情况相似。

图8(d)～图(f)分别为背风角度为60°至80°下燃烧器z=0和y=0截面的等值流线图。从图中可知，它们的流线分布相似。在y=0截面中，上下两侧形成了一对对称的旋涡，然而在z=0截面中，上下两侧形成的旋涡并不非常对称。其旋涡左侧流线明显背离涡心，呈发散状，表面涡旋强度低且不稳定。同时，其回流区长度逐步增加，回流区面积也逐步增大，总压损失也随之增加。

图8(g)为背风角度为90°下燃烧器z=0和y=0截面的等值流线图。在z=0截面和y=0截面中，上下两侧都形成了较为对称的两对旋涡。一对小旋涡的产生使得燃烧器出口总压损失增大，同时其回流区长度大，回流区面积大，总压损失也增大，再者这是没有渐变过程的突扩，使得出口总压损失系数相对其他工况有一个明显上升。

2.6 湍动能分析

湍动能是影响火焰传播的一个重要因素［15］。湍动能主要来源于时均流，通过雷诺切应力做功给湍流提供能量。选取z=0截面进行分析。

由于背风角度为30°时，流场内会出现没有回流涡的情况，不能提供稳焰条件。由图9(a)可知，背风角度为40°时突扩口后部产生大尺度旋涡使得回流区内有较高的湍动能，旋涡中心湍动能最高，并从中心向外递减。图9(b)和图9(c)分别为背风角度为60°和90°时的湍动能分布情况。因为随着背风角度增加旋涡中心向后移动，所以湍动能最高值也向后移动，其分布规律也是旋涡中心湍动能最高，并从中心向外递减。其他工况的湍动能分布均类似于40°的。

旋涡中心湍动能如图10所示。从图中看出，90°时湍动能最高，即时均流的能量在这个区域损失比较大，从而再次解释了90°时总压恢复系数阶跃上升的现象;其次是40°的情况，虽然其湍动能较大，但是总压损失最小。另一方面，较高的湍动能能够促进区域内传热传质过程，使得燃烧更充分，出口流动参数也更均匀化。

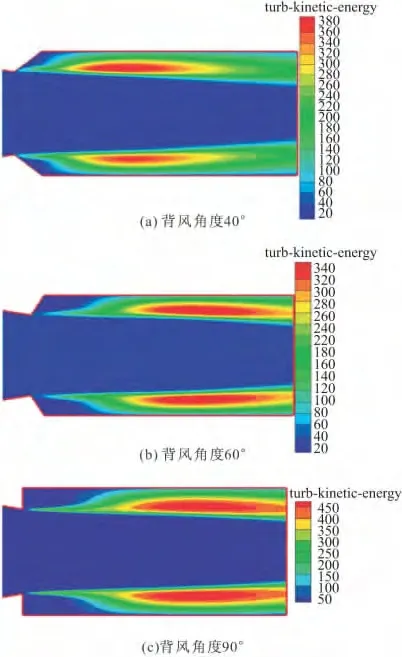
图9 不同背风角度z=0截面湍动分布

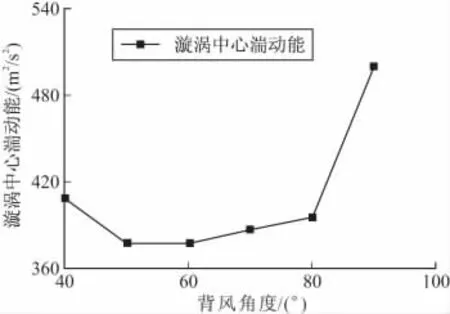
图10 不同角度旋涡中心湍动能

3 结论

文中在迎风角度和突扩比一定的条件下，对不同背风角度的沙丘形突扩燃烧室的流动特性进行了分析，得出以下结论:

1)总压损失系数随背风角度的增大而增加，在90°时由于台阶突扩，总压损失系数有一个明显的阶跃上升趋势。

2)背风角度越小，突扩口后部平均静压越高。

3)除背风角度90°外，其余背风角度下，都满足下列规律:(a)突扩回流区长度随背风角度增加而增大;(b)壁面附近最大返流速度随背风角度增加而减小。

4)在迎风角度和突扩比一定的条件下，存在一个最优的背风角度，在文中这个背风角度为40°。

［1］钟兢军，刘世青.驻涡燃烧室前驻体后端面冷态流场数值模拟［J］.热能动力工程，2010，25(5):482-486.

［2］伍波成，梁小平.突扩燃烧室流场及温度场的数值模拟［J］.重庆大学学报，1997，20(20):117-122.

［3］秦飞，何国强，刘佩进.突扩燃烧室低频燃烧不稳定控制方法［J］.推进技术，2011，32(1):59-64.

［4］章晓梅，夏允庆，单洪彬.低频振荡燃烧研究综述［J］.推进技术，1996，17(1):47-53.

［5］Lieuwen T C，Yang V.Combustion instabilities in gas turbine engines:Operation experience，fundamental mechanisms，and modeling［M］.USA:American Institute of Aeronautics and Astronautics，Inc，2006.

［6］杨岩岩，刘连友，屈志强，等.新月形沙丘研究进展［J］.地理科学，2014，34(1):76-83.

［7］江丽娟.新月形沙丘风场的数值模拟［D］.兰州:兰州大学，2005.

［8］张蓓.低雷诺数圆管突扩流场的数值模拟及阻力特性分析［D］.黑龙江:哈尔滨工业大学，2007.

［9］王福军.计算流体动力学分析［M］.北京:清华大学出版社，2007.

［10］李昊，林明，张玉山，等.中心突扩燃烧室PIV实验研究［J］.实验流体力学，2011，25(4):45-49.

［11］林宇震，许全宏，刘高恩.燃气轮机燃烧室［M］.北京:国防工业出版社，2008.

［12］彭泽琰，刘刚，桂幸民，等.航空燃气轮机原理［M］.北京:国防工业出版社，2008.

［13］陈超杰.可控涡扩压器的数值研究［D］.南昌:南昌航空大学，2013.

［14］Teysandier R G，Wilson M P.An analysis of sudden enlargement flow［J］.J.Fluid Mech.，1974，64:85-95.

［15］尹航，钟仕立，戴韧，等.钝体燃烧器湍流预混燃烧流动特性分析［J］.动力工程学报，2012，32(2):101-105.