小跨径钢筋混凝土简支系杆拱建模精度控制分析与应用场景建议

邓少伟

（广州交投城市道路建设有限公司 广州 510500）

0 前言

在桥梁结构分析建模方式的选择上，一般有杆系模型和实体有限元模型两种选择［1］。这两种建模方法各有特点：杆系模型其基本单元为两节点的杆系单元，常用在对整个桥梁结构体系的模拟，前处理阶段模型的大小及尺寸容易调整，便于从总体上把控，而且后期计算成果能够以杆系的弯矩、轴力、剪力直观地表达出来，同时也能输出构件边缘的应力，计算精度也能满足一般工程设计的要求，因而在梁、拱、柱等单一结构体系的计算中使用非常广泛。

实体有限元模型（以下简称实体模型），其基本单元形式多样，多采用八节点单位，常用在异型构件、特殊节点连接（例如梁拱结合部）等某些受力状况比较复杂、应力云图不规则这些特殊构件的模拟上，是对构件全维度的模拟，但模型建立和调整难度也比杆系模型高很多，往往需要在前处理阶段就要统筹考虑从细部到整体的布局，也由于这个原因导致实体模型很少用在桥梁整体模拟中。但是一旦采用实体模型完好模拟桥梁整体，由于模型中需要全面细致地模拟边界条件，而且结构体系的自由度是全维度的模拟，其计算成果（例如位移、应力）的精度都比杆系模型高；后期计算成果可以得出构件任意点上的应力和变形，从而判断出构件的哪个部位是薄弱区域，让设计人员予以避免，这也是实体模型的最大特点［2］。

如前所述，一般的单一构件，如梁、拱、柱在计算分析上采用杆系模型，其计算精度已经能满足工程需要。但是对于某些组合体系而言，采用杆系模型模拟与实体模型相比，会存在模拟精度稍低的问题［3］。例如系杆拱结构，在采用杆系模型模拟的基础上，其梁拱组合部节点的准确模拟将对整体的模拟精度带来积极影响，而且能够提高建模计算的便利性，具有较大的实用价值［4］。本文主要阐述小跨径简支系杆拱此类梁拱组合体系如何准确模拟组合节点，从而给计算分析上带来更高的准确性。其案例系杆拱的尺寸如图1所示。

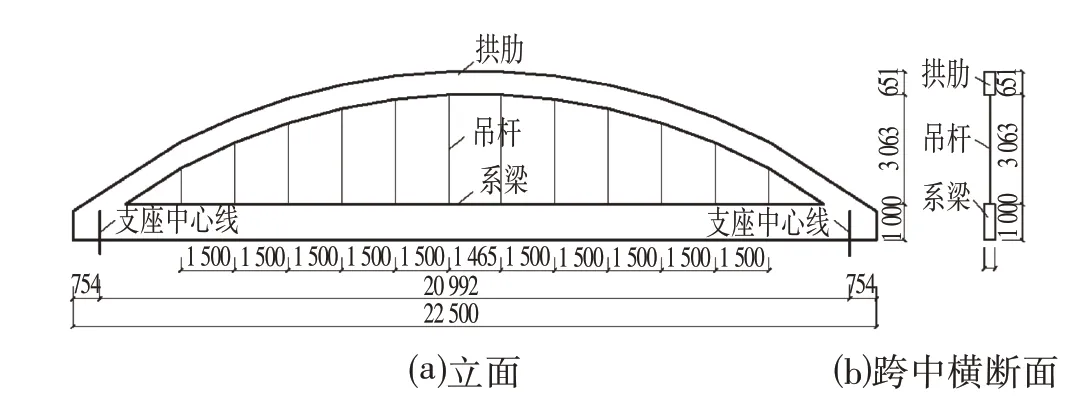
图1 案例系杆拱尺寸Fig.1 Dimension of Tied Arch in Case （mm）

1 五类系杆拱计算建模

1.1 模型1：全实体模型

对以上述尺寸采用大型有限元软件MIDAS CIV⁃IL 建立全实体模型，其中只受拉单元12 个（吊杆），八节点单元2 212个，节点4 012个，外部简支，并考虑桥梁的自身重力作用以及系梁面上100 kN/m2的面荷载（以下案例的荷载作用与此一致），据此建立的实体模型如图2 所示，模型各计算结果分列于表1、表2 进行比对。

表1 各模型位移对比Tab.1 Displacement Comparison of Each Model

表2 各模型内力对比Tab.2 Internal Forces Comparison of Each Model

图2 简支系杆拱实体模型Fig.2 Solid Model of Simply Supported Tied Arch

1.2 模型2：半实体模型

这是一种比较特殊的建模方法，主要体现在系梁、拱肋这样单一构件采用杆系模型模拟，拱梁结合部位采用实体模型模拟［5］。这种建模方式的难度与全实体建模相当，是除了特殊节点部位采用实体模型模拟，其余大范围的构件采用杆系模拟，既可以比较精确地模拟结构的受力，又能充分运用杆系模型在整体建模中的便利性。其中建立的系杆拱案例模型具有只受拉单元12 个（吊杆），梁单元144 个（系梁、拱肋），八节点单元320 个（梁拱组合节点），其模型如图3所示，模型各计算结果分列于表1、表2进行比对。

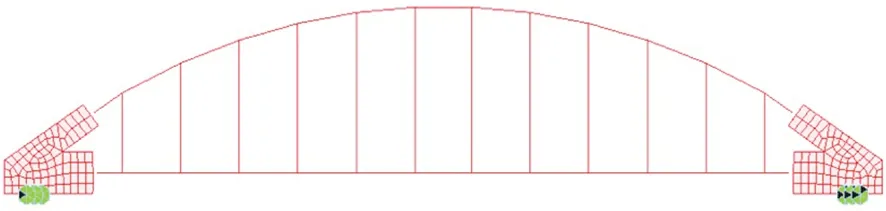
图3 简支系杆拱半实体模型（梁拱结合部实体）Fig.3 Semi Solid Model of Simply Supported Tied Arch

1.3 模型3：杆系模型I（未调整梁拱结合位刚度）

该模型直接采用梁单元模拟梁、拱，梁拱结合位仅为节点连接，未采用其他方式调整该处结合位刚度，其中只受拉单元12个（吊杆），梁单元151个，其模型如图4⒜所示，模型各计算结果分列于表1、表2 进行比对。

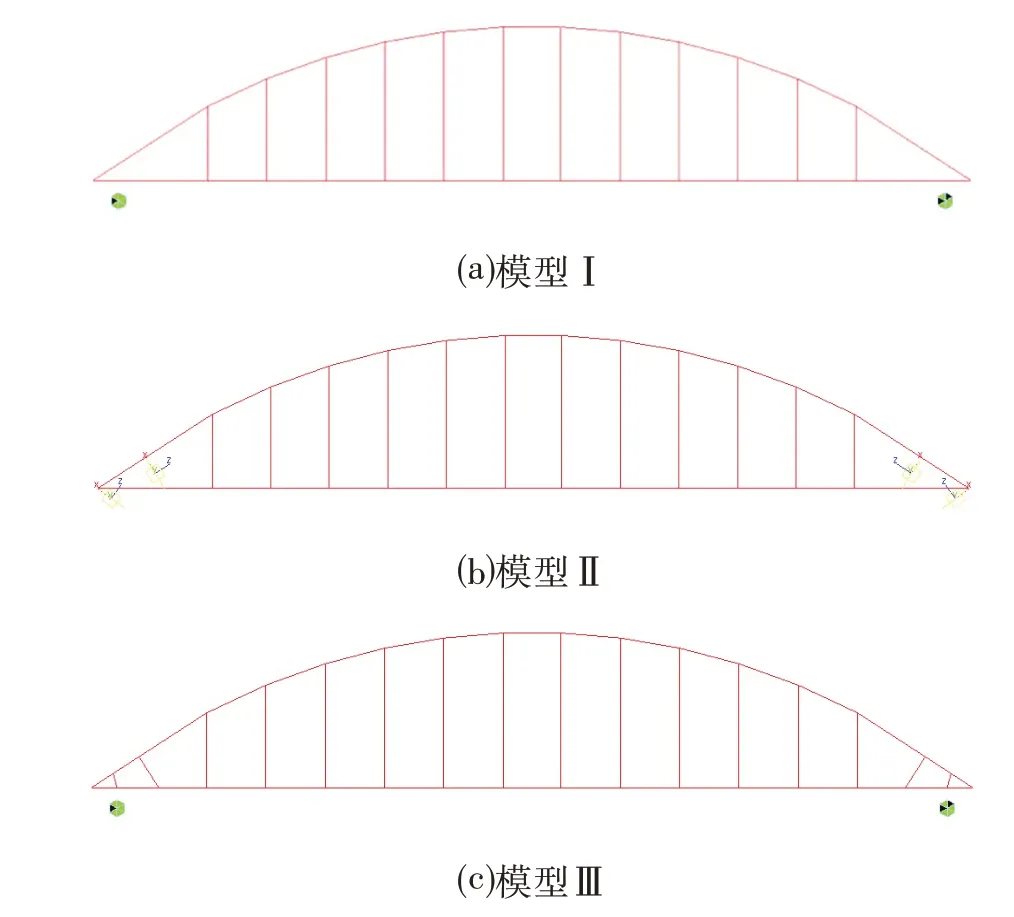
图4 简支系杆拱杆系模型Fig.4 Frame Model of Simply Supported Tied Arch

1.4 模型4：杆系模型Ⅱ（采用刚臂调整梁拱结合位刚度）

该模型相对系杆模型一，在梁拱结合位附近尝试采用了刚臂对结合位的刚度进行模拟，以反映该结合位的刚度对模型分析结果的影响程度［6］，其中只受拉单元12 个（吊杆），梁单元151 个，其模型如图4⒝所示，模型各计算结果分列于表1、表2进行比对。

1.5 模型5：杆系模型Ⅲ（采用梁单元调整梁拱结合位刚度）

该模型相对系杆模型一，在梁拱结合位附近尝试采用梁单元（此梁单元截面刚度与系梁梁单元一致）对结合位的刚度进行模拟，以反映该结合位的刚度对模型分析结果的影响程度，其中只受拉单元12 个（吊杆），梁单元156 个，其模型如图4⒞所示，模型各计算结果分列于表1、表2进行比对。

2 建模精度数据对比

以上各不同类型建模在相同边界条件和荷载（桥梁的自身重力作用以及系梁面上100 kN/m2的面荷载）作用下的位移和内力情况对比如表1、表2所示。

从上面分析可知，在系杆拱结构形式（即结构尺寸、材料性能、跨径、边界条件等）同等一致的情况下，不同的建模方法将导致拱梁结合点刚度有所不同，从而直接影响整个模型的刚度［7］。由于简支系杆拱是内部超静定结构，各单元上外力引起的内力值也会由于结构刚度分配上会有所不同。本次系杆拱建模精度分析，以实体模型为最接近结构真实刚度为判别前提，可以得出以下推论：

⑴半实体模型（端部实体）的下挠和内力跟实体模型几乎一致，但是其建模难度与实体模型相当，模型调整时比较困难，在实际工程中应用很少，主要作为本次实体模型某些难以表现的数据补充说明来判别以上3种杆系模型的优劣；

⑵杆系模型Ⅰ是最简易模型，未对梁拱结合位的刚度进行调整，仅采用单个节点来模拟，其刚度相对实体模型是3 种杆系模型中最小且偏离最大，位移数值较大，模拟精度稍低。但是由于其数值偏大，在计算上能得到较保守的验算结果，对某些特殊建模需要（例如需要进行维修加固的桥梁）会有好处；

⑶杆系模型Ⅱ是在杆系模型I 的基础上在梁拱结合位附近采用刚臂来调整其刚度，造成结合位刚度偏大，导致整个模型刚度相对实体模型也偏大，造成位移数值偏小，模拟精度也稍低。这说明将梁拱结合位模拟成刚节点的做法并不合适，尤其对于一些小跨径的混凝土系杆拱更为不妥。

⑷杆系模型Ⅲ是在杆系模型I 的基础上在梁拱结合位附近采用梁单元（此梁单元截面刚度与系梁梁单元一致）来调整其刚度，从对比结果来看，其变形与实体模型非常接近，内力值与半实体模型的也基本一致，总体而言这建模方式模拟精度相对系杆模型I、Ⅱ有所提高，尤其是在结构整体刚度上与实体模型非常接近，说明采用增加梁单元方式调整梁拱结合位刚度，是提高系杆拱杆系模型模拟精度的一个很好的可行方向。

3 实例对照

广东梅州市梅江桥始建于1934 年，市二级文物，曾于20 世纪60 年代和2009 年分别进行过大修加固，现状桥型结构为钢筋混凝土简支系杆拱，矢跨比约为0.18，跨径分为22 m和19 m两种，共11跨（22 m有5跨，19 m有6跨）跨越梅江［8］。现状概貌如图5所示。

图5 梅江桥概貌Fig.5 Overview of Meijiang Bridge

2010年、2018年均进行过一次比较完备的动静检测试验。在此结合该实例实测数据［9-10］，在相同的边界条件、材料参数、荷载输入等条件下，比对仿照上述杆系模型I～Ⅲ进行建模所得出的各特殊断面的计算理论值，以此说明梁拱结合位的杆系模拟的区别及特点。

杆系模型建模分别运用大型有限元软件MIDAS CIVIL 建立单跨该桥加固有限元分析模型（仅上部结构），计算跨径22.5 m，其离散模型如图6所示。

图6 梅江桥主桥单跨杆系模型Fig.6 Frame Model of Meijiang Bridge

计算模型模拟采用与2010 年、2018 年静载试验工况一相同的2 辆15 t 试验车载布载方式，如图7 所示。各模型特殊截面挠度计算值与2010 年、2018 年静载试验实测值的比对如表3所示。

表3 各模型计算值与静载试验挠度实测值对比Tab.3 Comparison between Calculated Values of Each Model and Measured Values of Static Load Test Deflection

图7 工况一静载试验加载布置平面Fig.7 Loading Plane of Static Load Test （cm）

从表3 可见按“杆系模型Ⅲ”建模，其计算值与静载实测值更为接近，与章节2中的推论一致，可作为更符合静载试验的应用建模。

4 结语

由于简支系杆拱的自身结构特性，不同的建模方式将导致不同建模结果精度输出。通过上述的比较分析及实例比对，本文基本解决了小跨径简支系杆拱杆系模型特性引起的精度差异的问题，并提出不同应用场景采用不同建模类型的结论建议（见表4），可供同类工程的计算分析人员参考借鉴。

表4 各应用场景建模类型选取建议Tab.4 Suggestions on the Selection of Modeling Types for Each Application