基于事件触发的水下滑翔机自适应容错俯仰控制
2023-08-08闵博旭高剑井安言陈依民王佳润潘光
闵博旭, 高剑, 井安言, 陈依民, 王佳润, 潘光
(西北工业大学 航海学院, 陕西 西安 710072)
0 引言
水下滑翔机是一种浮力驱动的新型水下自主航行器,具有续航能力强、活动范围广、噪声小等特点,广泛应用于海洋资源勘探、军事侦察等重要任务[1]。自主控制是水下滑翔机完成预定任务的关键技术之一,由于其数学模型具有显著的非线性、不确定性、多变量耦合性和欠驱动性,如何实现稳定、准确、快速和低功耗的控制成为极具挑战性的问题。水下滑翔机的自主控制包括姿态角控制、路径跟踪控制和编队控制等[2-6]。其中,俯仰姿态控制直接决定水下滑翔机在纵平面滑翔运动的稳定性,受到许多国内外研究人员的关注。
天津大学海燕水下滑翔机团队针对水下滑翔机的姿态控制[2]、航向控制[3]、路径规划[4]和深平均流估计[5]等关键问题,较早地开展了一系列较完整的工作。例如文献[2]针对水下滑翔机纵向运动给出优化的滑翔角,并使用PID控制器对滑翔角进行跟踪,结果表明通过该优化控制策略能够显著提升水下滑翔机的运动性能。文献[6]对水下滑翔机6自由度非线性模型在平衡点处进行线性化,并使用PID方法对俯仰角进行控制,仿真结果验证了方法的有效性。文献[7]同样针对线性化模型,提出了俯仰角的线性二次型最优控制律,结果表明该方法具有较好的暂态和稳态性能。此外,还有学者基于系统辨识的思想辨识出俯仰角动态的含有时滞环节的传递函数模型,并基于模糊PID方法实现了良好的控制[8]。值得指出的是,以上方法均基于线性化模型设计线性控制律,而线性化模型无法反映俯仰运动非线性系统的全部特性,设计出的控制律往往只在平衡点附近具有有效性,且要求模型参数精确、已知,一旦模型参数发生漂移、摄动,控制律可能失效。
反步法(Backstepping)和滑模控制作为非线性系统的典型设计工具,也被成功应用于水下滑翔机的俯仰控制。文献[9]针对以滑块加速度为输入的模型设计了反步控制律,仿真结果表明其整体控制效果优于PID控制。文献[10]提出了两种基于滑模控制的控制律,从仿真结果来看滑模控制的控制抖振现象比较严重,不利于执行器的长期使用。文献[11]提出了自适应积分反步控制律,考虑了模型参数不确定性,并使用自适应参数对不确定参数进行估计,提高了算法的适应性和鲁棒性。文献[12]提出了基于自抗扰控制的方案,并使用强化学习技术对控制器参数进行在线优化。文献[13]提出了基于动态逆的控制方案,使用神经网络对建模误差进行在线补偿,进一步提高了对不确定动态的鲁棒性。
尽管上述非线性控制方案实现了对水下滑翔机俯仰角的有效控制,尚有3个问题需要进一步解决。
首先,上述方法均将水下滑翔机的模型参数及执行器增益视为已知,这与工程实践不符,也降低了控制算法对模型摄动和外界干扰的鲁棒性。尽管有学者提出具有自适应机制的控制律,但其仅考虑了参数不确定,即认为不确定项结构已知但参数未知或不准确,具有较大的局限性。基于滑模控制的方案需要已知模型不确定项的上界,且其抖振问题不利于执行器的长期使用。近年来,神经网络和模糊逻辑系统由于具有对非线性函数的良好逼近性能,被广泛应用于不确定非线性系统的控制中[14-15],许多学者更是将其应用于海洋运动体的控制中[16]。采用基于逼近器的自适应控制方案可以进一步提高水下滑翔机控制算法在模型具有任意不确定性时的鲁棒性。
其次,水下滑翔机在执行任务的过程中可能发生执行器故障。这就要求所设计的控制算法具有一定的容错能力,使水下滑翔机在故障情况下依然能安全滑翔至预定位置。目前有关水下滑翔机容错运动控制的研究较为有限。
最后,目前提出的控制方案均为连续控制律或称为时间触发控制律。由于外界干扰和自身不确定性的作用,用于控制俯仰角的滑块不会停留在平衡位置,而是会在其附近做连续的移动,以保证俯仰角维持在预定的角度上。滑块的连续移动不仅意味着严重的控制器到执行器的通信资源浪费,也造成了更多的执行器磨损和能量消耗,同时滑块移动产生的噪声也会影响声学设备的工作。水下滑翔机作为一种自带能源的水下航行器,必须尽可能地减少控制系统能耗,以保证较长的航程。引入事件触发机制[17]使得控制器到执行器的信号并不依赖时间的激励进行更新,而是仅当预先设置的触发条件被满足时才进行更新,因此能有效地节约控制器到执行器的通信资源,减少执行器的动作次数和频率,从而达到节能和保护执行器的效果。文献[17]提出了对非线性系统进行事件触发设计的通用框架。目前较多使用的事件触发条件有固定阈值型、相对阈值型、混合型、自触发控制、周期触发等。其中,固定和相对阈值型条件已被广泛应用于严格反馈系统的事件触发控制,以及欠驱动水面船的事件触发路径跟踪控制[18]。
受以上成果的启发,本文提出一种基于事件触发的水下滑翔机自适应容错俯仰控制方案。在传统反步法框架下,考虑俯仰运动动力学模型不确定性和未知外界干扰,使用基于系统历史输入、输出数据的神经网络逼近器对未知非线性函数和执行器故障进行整体逼近,保证控制算法的适应性和鲁棒性。最后,设计了基于相对阈值的事件触发条件,降低了通信资源占用和执行器动作频率,减少了能量消耗。基于Lyapunov理论证明了系统所有信号满足半全局一致最终有界(SGUUB),同时证明了最小触发间隔的存在性,避免了“芝诺”行为。
1 基础知识
1.1 水下滑翔机俯仰运动数学模型
如图1所示,水下滑翔机纵向运动可以由大地坐标系Oxyz和附体坐标系Obxbybzb描述。图1中:原点O选在地球表面任意一点,Ox轴指向正北,Oy轴垂直于Ox轴指向天,Oz轴指向正东;原点Ob选在浮心,Obxb轴沿着纵轴,正向指向头部方向,Obyb轴垂直Obxb轴指向上,Obzb轴垂直于Obxb和Obyb轴指向右;θ为俯仰角,以水下滑翔机抬头为正,α为攻角,v为水下滑翔机在纵平面内的合速度。

图1 水下滑翔机运动坐标系
根据文献[19],水下滑翔机俯仰角控制回路的数学模型可以表示为
(1)
式中:ωz为俯仰角速度;Jzz为惯性矩;λ66为附加惯性矩;m为水下滑翔机总质量;xc为重心的纵向坐标,其与滑块的纵向坐标之间满足如下线性关系:
xc=kxcxpmp/m+xc0
(2)

为便于控制器设计,将水下滑翔机俯仰运动模型式(1)表示为如下严格反馈系统形式:
(3)

(4)

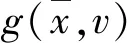
假设2未知干扰d是有界的,即存在dmax满足|d|≤dmax,dmax同样为未知的正常数,仅用于稳定性分析。
1.2 径向基函数神经网络
径向基函数神经网络(RBF-NN)由于其良好的非线性映射能力,被广泛用作函数逼近器。本文使用RBF-NN处理水下滑翔机模型中的复合不确定项。
引理1对于任意给定的连续函数f(x),可以使用RBF-NN对其按照如下形式进行逼近[14-15]:
f(x)=WTφ(x)+ε, ∀x⊂Ωx
(5)
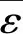
(6)
μi为高斯函数的中心值,ηi为高斯函数的宽度;Ωx为紧集。根据通用逼近定理,在紧集Ωx上存在理想权重W*,使得RBF-NN对非线性函数以任意精度进行逼近,即满足下式:
(7)
式中:W*为理想存在的未知量,因此需要对其进行在线估计;Rl表示l维实数空间。
引理2对于形式满足式(8)的多输入多输出(MIMO)非线性系统,其未知非线性函数f(X1,X2,t)可以使用RBF-NN按照式(9)的形式进行逼近[20-21]:
(8)
f(X1,X2,t)=WTφ(ξ)+ε(ξ)
(9)

2 自适应容错控制器设计
结合式(3),给出考虑执行器故障输入的水下滑翔机俯仰运动数学模型如下:
(10)
式中:uf为考虑执行器故障的输入,可进一步描述[22]为
(11)
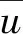


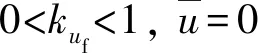

假设3在综合考虑模型不确定项、有界环境扰动和式(9)描述的执行器故障的情况下,水下滑翔机俯仰运动是可控的。
在考虑以上所述扰动时,需要系统仍然满足可控性,即在饱和约束范围内,执行器能提供足够的控制输入以补偿复合扰动,否则无法实现稳定控制。
定义俯仰角跟踪误差变量z1=x1-xd,xd为需要跟踪的目标俯仰角,则有
(12)
设计x2的虚拟控制律,即参考俯仰角速度,如 式(13) 所示:
(13)
k1为正的调节参数。为避免对虚拟控制律直接求导,解决水下滑翔机切换姿态时参考信号不连续的问题,并对跟踪误差进行滤波处理,使用动态面技术[22]。令α1通过式(14)所示的1阶滤波器,并定义俯仰角速度误差变量z2=x2-q1和滤波误差y1=q1-α1,q1为动态面变量,
(14)
式中:τ1为滤波器的时间常数。结合式(13)、式(14),将误差变量z1的动态改写为
(15)
(16)
由Young不等式,
(17)

(18)
式中:Br(·)为具有上界Mr的连续函数,满足|Br(·)|≤Mr。同样由Young不等式,有
(19)
a3为设计常数。将式(17)、式(18)、式(19)代入式(16),可得
(20)
为便于控制器设计,将式(10)中水下滑翔机俯仰角速度x2的动力学表达式进一步改写为
(21)
对俯仰角速度跟踪误差z2=x2-q1求导,可得
(22)
(23)

3 事件触发控制律设计
为进一步降低执行器动作频率,减少控制能耗并节约控制器到执行器通道的通信资源,设计如下相对阈值事件触发条件:
u(t)=v(tk),∀t∈[tk,tk+1)
tk+1=inf{t>tk||e(t)|≥λ|u(t)|}
(24)
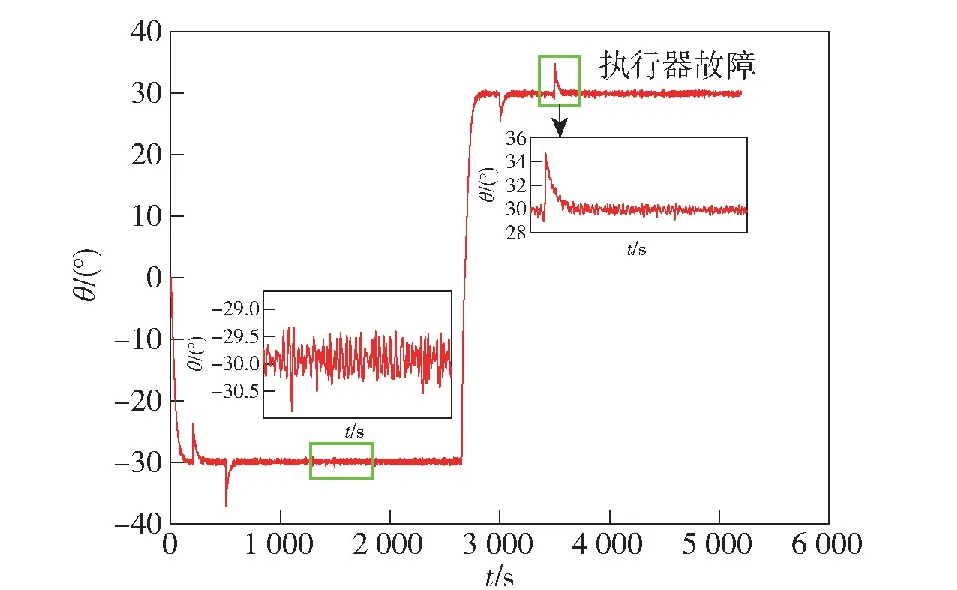
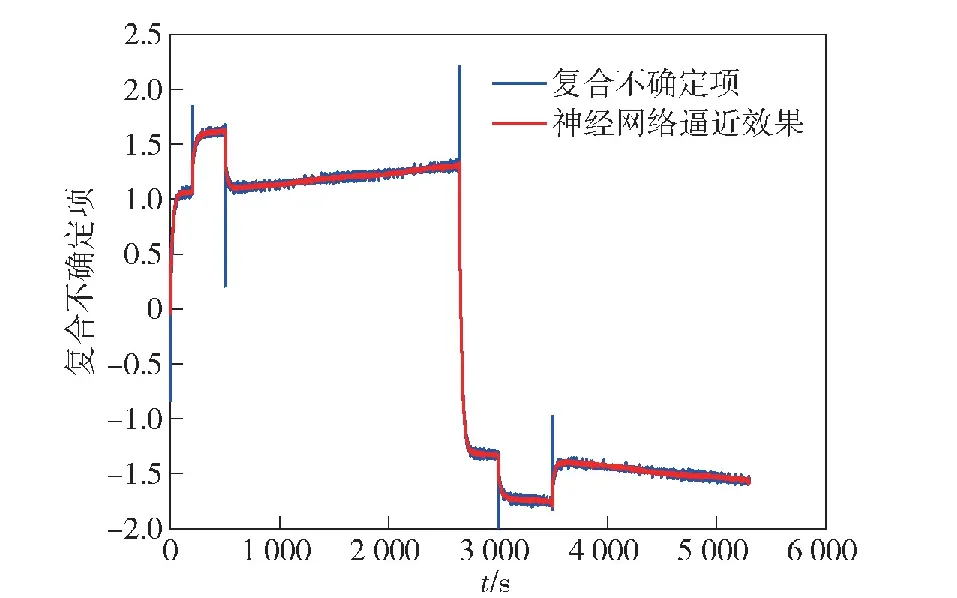
式中:u(t)为执行器实际输入信号;v(tk)为待设计的滑块位置命令信号;e(t)=v(t)-u(t)为事件触发采样误差;λ为取值0~1之间的事件触发相对阈值参数。显然,在tk≤t (25) 式中:η(t)为未知变量,η(t)∈[-1,1]。结合式(23)、式(25),将式(22)改写为 (26) 设计滑块控制命令v(t)的表达式如下: v(t)=vm(t) (27) (28) 式中:vm(t)为中间控制律;k2为大于0的调节参数;为对最优权重的估计,估计误差为对1+η(t)λ的估计,其自适应律设计为 (29) (30) 式中:Γw为学习速率参数;σw为修正系数,保证参数有界。 本文设计的事件触发自适应容错控制律相比传统的自适应反步控制具有如下两点优势:1)同时考虑了模型未知非线性函数、未知控制增益、环境扰动和执行器故障,使用数据驱动的神经网络逼近器对复合不确定项进行补偿,提高了算法的鲁棒性和适应性;2)首次将事件触发技术引入水下滑翔机运动控制中,设计了控制器到执行器通道的事件触发条件,进一步节约了控制能耗和通信资源。 使用Lyapunov理论证明闭环系统的稳定性和最小触发间隔的存在性,主要内容总结为定理1。 证明选取闭环系统的候选Lyapunov函数 (31) 对其求导,得到 (32) (33) 式中: (34) 将式(34)代入式(33),可得 (35) 含有估计误差的两项可以用自适应律式(29)、式(30)分别补偿,得到 (36) 和 (37) 由Young不等式放缩,可得 (38) (39) (40) 将式(37)~式(40)代入式(35),可得 (41) 定义以下两个参数以构造微分不等式: (42) (43) 由此可知闭环系统所有信号满足半全局一致最终有界,通过适当的调整参数能使得跟踪误差任意小,即水下滑翔机的俯仰角在考虑模型不确定性、环境扰动和执行器故障的情况下能有效跟踪参考俯仰角。 下面证明最小触发间隔的存在性。考虑到对于任意时刻有|v(t)-u(t)|≤λu(t)成立,对|e(t)|求导,可得 (44) 选取某型水下滑翔机6自由度数学模型开展仿真实验,以验证本文提出算法的有效性。该水下滑翔机长5 m,质量600 kg,用于俯仰控制的滑块质量40 kg。使用完整的6自由度模型进行仿真,对于控制器设计相当于产生了模型摄动,用于检验控制器的鲁棒性。此外,使用白噪声驱动2阶传递函数模拟未知环境扰动,即 (45) 式中:s为拉普拉斯算子;wH为高斯白噪声。 执行器特性方面,滑块位移的幅值限制为0.05 m。控制器参数选取如下:k1=0.1,k2=0.02,Γw=0.1,σw=0.001,Γχ=0.05,σχ=0.02,τ1=0.01。事件触发条件参数λ=0.02。RBF-NN的宽度b=0.3,含有10个节点,其中心均匀分布在[-0.02,0.02]×[-0.02,0.02]×[-0.05,0.05]上。 图2 俯仰角控制效果 图2给出了存在执行器故障情况下的水下滑翔机俯仰角控制效果。图3为控制输入曲线,即滑块指令位置和故障情况下的滑块位置。图4为水下滑翔机的纵平面运动轨迹。图5给出了事件触发间隔情况。图6给出了包括模型不确定项、环境扰动和执行器故障的复合不确定项以及神经网络的逼近效果。 图3 滑块位置 图4 水下滑翔机纵向运动轨迹 图5 事件触发间隔 图6 复合不确定项及神经网络逼近效果 从俯仰角控制情况来看,本文设计的自适应容错控制器具有较好的动、静态性能。动态性能方面,能迅速跟踪参考俯仰角,完成姿态切换。静态性能方面,具有较小的静态误差,在0.5°以内,符合精度要求。从图6中可以看出,本文设计的基于历史输入输出数据的神经网络能够对复合不确定项进行良好补偿,俯仰控制具有良好的适应性和鲁棒性。在执行器故障发生后,基于数据驱动的神经网络能快速地对执行器故障的影响进行估计和补偿,并相应地调整滑块的平衡位置,使跟踪误差在短时间内收敛至平衡点,实现容错控制。从图4给出的水下滑翔机运动轨迹来看,本文设计的控制律能有效完成对目标俯仰角的跟踪,在存在不确定性以及执行器故障的情况下依然能实现纵平面稳定的滑翔控制。 从控制输入的情况看,本文设计的相对阈值事件触发条件有效地降低了滑块位置的更新频率。从图3及其局部放大图给出的滑块位置看,实际控制输入呈阶梯状,其更新不依赖于时间的激励而是仅由事件触发条件决定。从图5给出的事件触发间隔来看,最大触发间隔为203 s,最小触发间隔为 0.01 s,说明“芝诺”行为被很好地排除。事件触发情况下执行器信号累计更新1 307次,而在时间触发情况下按照0.01 s的采样周期需要更新520 000次,表明事件触发控制能减少90%以上的控制器至执行器通道信号传输,同时滑块移动的减少也意味着更好的节能效果。本文设计的控制律在保证控制效果的前提下得到了较大的触发间隔,这也得益于水下滑翔机纵向运动自身的稳定性。 本文针对水下滑翔机俯仰姿态控制中存在模型不确定性、执行器故障以及控制更新频繁能耗大的问题,提出了一种基于事件触发的自适应容错俯仰控制方案。仿真结果表明,利用数据驱动神经网络可以对包括执行器故障作用的复合模型不确定项进行有效估计和补偿。利用事件触发机制能减少控制器到执行器通道的信号传输,避免执行器状态频繁改变,对实现水下滑翔机的节能控制具有重要意义。在下一步研究中,将设计浮力驱动水下滑翔机的事件触发航向保持控制方案。
4 稳定性及芝诺行为分析
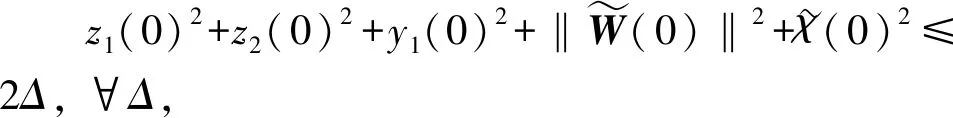
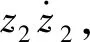

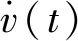
5 仿真实验




6 结论
