一题多用，落实“双减”政策的新路径

陈伯梅

摘  要：减轻学生作业负担与校外培训负担，是当前初中数学教学的基本要求。为此，教师在教学中要改变以往的教学策略，以切实减轻学生的学习负担，提高他们的学习能力。一题多用，不仅能减少学生作业的数量，还能有效提高学生的思维品质。教师可以在具体的教学环节设置一题多用，激发学生的探究兴趣，让他们从传统的题海战术中跳出来。

关键词：“双减”政策；初中数学；一题多用

“双减”政策的出台就是使作业布置更加科学、合理，学生的学习回归校园，着眼学生身心健康成长，促使他们长远、可持续地发展。然而，当前初中生的数学作業依旧繁多，不仅不利于践行“双减”政策，还不利于促进学生的全面发展。一题多用，从学生的角度看可以是一题多变、一题多解、一题多想；从教师的角度看可以是一题多讲、一题多问、一题多评。总之，一题多用就是充分利用学生现有的题目资源，挖掘他们思维的潜力，促进他们多角度、全方位地思考，进而提高他们的学习能力。

一、一题多用，想一想其他解法

学生在完成作业时会形成思维定式，即将教师布置的作业完成了，相关的思考也就结束了。其实，教师还需要指导学生想一想有没有其他的解法，这样能激发他们思考，提升他们思维的深度。在传统的数学教学中，教师习惯性地布置许多作业，学生只有解答的时间，几乎没有更多的时间去思考。教师要改变这样的状况，减少作业的数量，增加作业的思维量。

例如，教师可以布置这样的作业：今有井，径五尺，不知其深，立五尺木于井上，从木末望水岸，入径四寸，问井深几何？这是《九章算术》中著名的井深问题。这道题的难度在于要先将文言文转化为现在的文字，还要将文字转化为图形。这两个步骤完成了，这道题也就基本解决了。

“双减”背景下的作业布置要减少数量，提高质量。解答这道题，学生需要运用一定的文言文知识，以及数学中的数形结合思想。依据题目内容画出图1

后，学生要做的就是将相关数据在图1中标出来，再将问题用数学语言表述出来。

学生是这样表述的，已知四边形BCDE是矩形，BE = 5，AB = 5，BF = 0.4，求BC的长。有的学生这样想：因为四边形BCDE是矩形，所以BF∥CD，进而推出△ABF ∽ △ACD。接着，依据相似的性质，得出AB ∶AC = BF∶CD。再由BC = AC - AB最终得出井深BC为57.5。学生做完此题之后，教师追问有无其他的解法。学生思考之后发现可以证明△ABF与△DEF相似，进而依据相似的性质求解BC。可见，教师在布置作业时要在减轻学生负担的同时多启

发他们的思维，以使他们的解题能力得到提高。教师在关注学生解法的同时也改变了他们评价作业的态度，教师更多地关注着学生的解题过程而不单是结果。在具体的解题过程中，学生先做什么，再做什么，往往不同，教师都可以引导学生深入思考，依据不同的思考得到不同的解法，以增强他们的获得感。

二、一题多用，想一想其他题目

初中生作业负担重的主要原因是作业数量多，即使教师不布置作业，家长也会布置作业。布置作业的目的在于提高学生的数学成绩。也就是说，通过不断地做题，学生在识记的基础上获得了一些解题方法与技巧。学生的解题能力是在“题海”中提高的。如果教师对照布置好的作业，让学生自主思考是否还有类似题目，他们会主动归纳题目的特点，进而总结出同一类题目的特征。想一想有没有其他类似题目，能让学生主动建构同一类型题的解法，进而能在少做题目的基础上获得思维的深层次发展。换言之，以前需要做大量题才能获得的能力，现在可以借力一题多用的模式来解决。

仍以井深问题为例，教师可以让学生想一想类似的题目。学生首先想到的是《九章算术》里有没有类似的题目，他们在勾股这一章节里找到许多相关的题目。接着，他们会思考解决这些题目主要运用的是哪方面的知识，书里有没有与其相似度较高的题目。学生发现解决井深问题运用的是相似三角形和矩形的性质等知识。基于此，学生在书中发现这样的题目：今有邑，东西七里，南北九里，各开中门，出东门一十五里有木，问：出南门几何步而见木？同样地，学生将题目中的文字转化为如图2所示的数学题：矩形城池ABCD，东边城墙AB长9里，南边城墙AD长7里，东门点E和南门点F分别是AB，AD的中点，GE⊥AB，HF⊥AD，GE长15里，GH经过点A，求HF的长。

学生依据条件GE⊥AB，HF⊥AD，GH经过点A，推导出AF∥GE，AE∥HF，进而推出∠AEG = ∠HFA = 90°，∠EAG = ∠FHA，由此可以得出△GEA ∽ △AFH。接着，他们从相似三角形这一结论入手，得出GE ∶AF = AE∶FH。将AB = 9，AD = 7，GE = 15这些条件带入，得出HF = 1.05。学生将这两道题进行比较，发现这两道题表面上的情境完全不一样，但是本质上是一样的，即都需要构图，求证相似，再得出线段比。有了这样的一题多用，在减轻学生负担的前提下，他们的数学思维获得发展。

三、一题多用，想一想新的反思

在布置数学作业时，教师可以将反思作为一项内容穿插其中。也就是说，教师要改变学生只做作业不反思的现象。反思就是让学生在做完作业之后，再想一想，并将自己的感想说出来。感想既可以是解题的经验，又可以是教训；既可以有思维的闪光点，又可以有思维上的短板。反思的目的是能充分挖掘题目的价值，让学生在少做题的情况下，获得更多的领悟，思维获得发展。

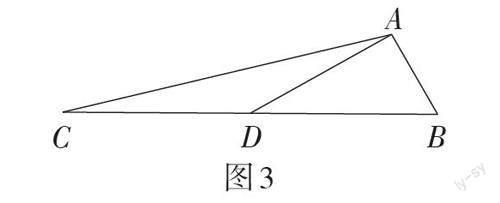
以教师布置的一道作业题为例。如图3，在△ABC中，D为BC的中点，AB = 5，AD = 6，AC = 13，求证：AB⊥AD。

对于这样的题目，部分学生束手无策，不知道从哪儿入手。他们的反思是这样的：这道题要求证垂直，其实就是要求相应的角为直角。题目中的条件只有三条线段的长，无法构成证明直角三角形的条件。学生的反思将解题中的困惑写了出来。对照学生的反思，教师反问：能不能从这些给出的数值上下功夫。学生将这些数值一一列出来，他们发现正常情况下5，12，13这三条边组成的三角形是直角三角形，将AD = 6延长一倍就能创造出一个直角三角形。于是，如图4，延长AD至点E，使AD = DE，连接CE，BE，可证得四边形ABEC是平行四边形。在△ABE中，AE = 2AD = 12，AE2 + AB2 = 52 + 122 = 132 = BE2 = AC2，所以△ABE是直角三角形，即∠BAE = 90°，得AB⊥AD。做完后，学生再次反思时写道：要充分利用条件，敏锐地察觉条件背后的奥秘，尽可能地借助辅助线将条件利用起来，将问题转化成可以解决的样式。

综上所述，教师在布置作业时要站在学生的角度思考问题，不能只将学生的成绩放在重要的位置，而要敦促他们全面发展，要发展他们的数学核心素养。一题多用能实现教师与学生在题目“使用”上的互动，进而更好地促进学生思维的发展，也能让教师更好地发展他们的数学能力，为进一步布置高质量的作业作铺垫。同时，一题多用改变了学生的学习方式，他们不再追求做题的数量，而是开始关注做题时思维的深度与广度。可见，教师要在一题多用上下足功夫，让数学学习由浅层学习走向深度学习，让作业的内容和形式由机械单一走向丰富多元。

参考文献：

［1］陈华萍. 一题多变天地宽：初中数学培养学生创造性思维和探究能力的实践与思考［J］. 考试周刊，2017（40）.

［2］赵亮. “一题巧用”促进科学思维的发展［J］. 数理化解题研究，2021（17）.