真三向应力作用下深部储层砂岩渗透率各向异性实验研究1)

2023-08-06王者超易云佳闵忠顺

力学学报 2023年7期

王者超易云佳闵忠顺冯浩

* (辽宁省深部工程与智能技术重点实验室,沈阳 110819)

† (中国石油天然气股份有限公司辽河油田分公司,辽宁盘锦 124000)

引言

地下储气库是解决城市用气短缺,有效调节用气峰谷差的特殊地质体,然而,由于我国地下储气库储层埋深较大,应力条件复杂,且均质性较差,因此建设和运营都面临着一定的挑战[1-3].地下储气库储层岩石的渗透率是制定储库注采气方案时的重要参数.准确表达储层渗透率是储气库生产运行中的关键问题[4].地下储气库的储层主要由砂岩等沉积岩组成.在沉积过程中,岩石颗粒会按照水流方向排列,导致颗粒的长轴主要平行于该方向.因此,储层砂岩在结构和性质上呈现出各向异性[5-6].通常认为,储层砂岩中的渗透率各向异性是由具有优先取向的粒级或层级非均质性引起的,特别是在硅质碎屑砂岩中更为明显[7].层状非均质性可能导致储层连续层的渗透率相差几个数量级,并呈现出明显的各向异性[8-9].另一方面,地下储气库具有强注强采的特点.随着储层深度和注采气强度的变化,储层应力和孔隙压力也会不断变化.在这个过程中,储层的静态结构会发生变化,从而影响孔隙中正常的流体流动,并诱导储层渗透率的各向异性[10].因此,研究储层砂岩的渗透率及其各向异性在施加总应力和孔隙压力下的变化规律是一项非常必要的工作.这项研究对于储气库的高效建库和安全运行具有重要的指导意义.

总应力和孔隙压力对岩石渗透率的影响以及岩石渗透率各向异性一直是岩石力学和渗流领域的重要研究内容之一.目前,对于岩石渗透率的实验研究主要涉及砂岩[11]、煤岩[12]、页岩[13]和花岗岩[14]等不同类型的岩石.国内外的许多学者已经对岩石渗透率随总应力或孔隙压力的变化规律进行了大量的研究工作[15-20].Wang 等[21]等通过力学实验发现,砂岩渗透率随压力的变化幅度很大,最高可达50%,此外,还建立了压力与岩石微孔结构变化的关系.乔丽苹等[22]提出一种新的有效应力原理,并通过实验测定多组不同外部应力条件和孔隙压力条件下岩石的渗透率,得出渗透率与孔隙压力存在指数关系.近年来,随着真三轴渗流实验装置的不断发展,国内外学者已经开始开展真三向应力状态下的三维渗透率测试研究.李铭辉[23]通过分析岩石的应力关系,推导真三向应力下储层岩石渗透率与各主应力的关系,并开展渗透率实验对提出的渗透率模型进行了验证.张羽等[24]研究真三向应力状态下立方体煤样渗透率敏感性,发现真三向应力作用下煤样水平最大主应力对样品水平方向渗透率的影响程度大于水平最小主应力.Li 等[25]对3 种主应力对渗透率的影响进行了实验研究,发现渗透应力敏感系数与应力状态和加载路径无关,并提出渗透率张量主分量的对数与主应力之间的线性关系.Nasseri 等[26]利用真三轴地球物理成像仪对枫丹白露砂岩进行了静水压力、常规三轴和真三轴状态下的流固耦合实验,研究不同 σ2/σ3应力比对渗透率的影响.

另一方面,在岩石渗透率各向异性方面,也已经取得了一系列的研究成果[27-30].Clavaud 等[31]研究砂岩孔隙空间几何形状对渗透率各向异性的影响,发现砂岩的渗透率各向异性与层理的存在有很好的相关性.Benson 等[18]在静水压力条件下研究孔隙空间各向异性与岩石渗透率各向异性之间的关系,不同类型的砂岩在垂直于层理和平行层理方向的渗透率存在明显的各向异性.Chen 等[32]首先研究砂岩气层开采过程中渗透率各向异性的演化,然后改进各向异性条件下基于砂岩应力应变的渗透率模型,最后定量研究渗透率各向异性比对侧向井网的影响.

通过这些研究成果可以发现,以往许多渗透率测量工作大都是在单轴应力条件或常规三轴应力条件下进行的.目前,国内真三向应力下的三维渗透率测试研究还处于初步阶段,因此对于在真三向应力作用下的渗透率演化规律的研究还相对较少.而地下储气库储层所处的真实应力场是三向不等压的,研究储层在真三向应力下的渗透率演化规律十分有必要.此外,以往的研究主要集中在渗透率与主应力的相互关系,有关真三向应力下孔隙压力与岩石渗透率的关系、孔隙压力引起的渗透率各向异性的研究工作较少,当涉及孔隙压力的作用时,学者们普遍根据Terzaghi 有效应力原理将其等效处理.国外学者Carroll[33]推导有效应力定律,用来描述孔隙流体压力对各向异性饱和多孔岩石线弹性响应的影响,指出了对于一般各向异性,有效应力和施加总应力之间的差异不是静水压力.因此,孔隙压力对岩石渗透率各向异性的影响是不可忽略的.

本文针对储层砂岩渗透率原生各向异性和诱发各向异性,开展真三向应力条件下总应力和孔隙压力共同作用下的储层砂岩渗透率演化的实验研究,采用稳态法测量真三向总应力和孔隙压力共同作用下储层砂岩的三维渗透率,分析储层砂岩的三维渗透率的演化规律和渗透率的各向异性特征,为地下储气库储层的评价和储气库运行提供重要参数和参考依据.

1 研究方法

1.1 样品准备

实验岩芯取自中国东北部S6 储气库竖直井储层段,S6 储气库储层地层构造带为北东向长轴背斜,构造幅度-2320～-2700 m,地层倾角3°～13°.岩芯采样深度为-2462～-2480 m,岩芯层理构造比较明显,在有明显层理的部位沿水平方向加工了5 块25 mm×25 mm×50 mm 的长方体标准样品,加工时让长方体一组25 mm×50 mm 的端面沿着岩芯的层理面.建立笛卡尔坐标系OXYZ,使Z轴垂直于样品的层理面,假设垂直层理方向为砂岩的一个渗透率主值方向,并且假设垂直层理方向的渗透率主值为kz,让长方体样品另外两组端面分别垂直于X,Y轴,这样有利于后续的渗流实验确定样品互相垂直的3 个平面上渗透率的差异,便能获取岩样渗透率的各向异性信息.原始岩芯及实验样品见图1.本研究使用Axioskop 40 Apol 偏光显微镜对样品进行薄片鉴定,确定它的矿物组成.实验所选用的砂岩可定义为长石砂岩,它的矿物学成分主要有石英60%、长石25% (斜长石、微斜长石和碱性长石)、岩屑15%(黏土岩屑、硅质岩屑和变质岩屑)、少量云母样品孔隙度采用真空饱水法测量,样品孔隙度和密度见表1.样品孔隙度的范围为17.781%～19.932%,样品的密度在2.016～2.079 g/cm3之间.

表1 砂岩样品的孔隙度和密度Table 1 Porosity and density of sandstone samples

图1 原始岩芯和样品Fig.1 Original core and specimen

1.2 渗透率测量方法

目前,测量岩石渗透率的主要方法包括稳态法和瞬态法(压力脉冲法).其中,稳态法包括基于入口/出口端的压力和基于入口/出口端的气体流量这4 种方法[34].国内相关研究大多数是基于出口端流量法[35-36],这种方法对测试仪器要求比较低且渗透率计算简单,缺点是当测试介质渗透率低于10-18m2时,出口端的流量很小.压力脉冲法采用变化的压力信号,如果压力梯度相同,其孔隙流体的扩散速度大于稳态法,并且这个方法的压力平衡时间和脉冲压力的大小都会影响测试结果的准确性.对高渗样品而言,压力平衡时间非常短不能保证测试结果的可靠性.考虑到本实验所用砂岩孔隙度大,渗透率相对较高,因此选用基于出口端流量的稳态法作为渗透率测试方法.

基于出口端流量的稳态法渗透率计算公式如下[34]

式中,k为渗透率;μ为气体的动力黏度;Q为出口端气体流量;A为气体渗流面的样品横截面积;l为样品长度;Pin为样品上游的气体压力;Pout为样品下游的气体压力.

当流量计测得的流量达到稳定时,记录此时的平均流量Q,则可以计算得到样品的渗透率.

1.3 实验装置

实验设备采用东北大学自主研制的两刚一柔型硬岩真三轴应力-渗流耦合装置,实验设备示意图如图2(a)所示.该装置主要由伺服加载系统、气体渗流系统、三轴压力室和测试系统4 个部分组成.其中设备的最大主应力和中间主应力通过轴向压头提供,最小主应力通过液压油泵提供,压力室内部采用了专门的渗流夹具,如图2(b)所示.设备输出的最大应力 σ1,σ2和 σ3分别为1200,1200 和100 MPa,加载框架的刚度大于16 GN/m.通过高精度线性可变位移传感器(LVDT)监测记录样品的变形,通过调节减压阀和背压阀组合控制被测岩样中的气体压力,气体管路系统所能承受的最大气压为8 MPa.压力室的气体管路上下游端均安装了高精度气体压力传感器(型号MIROSENSOR M20,量程0～10 MPa,精度0.1% FS)监测气体压力,出口端安装了体积流量计(型号Sevenstar CS200,量程0～10 m/s,精度0.2% FS)测量出口端的气体流量.

图2 硬岩真三轴应力-渗流耦合装置Fig.2 True triaxial stress-seepage coupling device for hard rock

1.4 应力水平选取

在地下储气库的实际运行中,除了井口附近的储层,大范围的储层均处于弹性变形状态.本研究将施加的总应力水平控制在砂岩的弹性范围内.此外,渗流实验考虑了对同一块样品进行X,Y,Z3 个方向的3 次渗透率测试,但为尽量减小每次实验对后续实验的影响,最大加载应力也应保证砂岩变形在弹性范围内.因此,先测量了砂岩岩样的真三轴应力应变曲线.真三轴压缩实验施加的中间主应力和最小主应力根据储气库运行期间储层最小有效应力确定,其中 σ2和 σ3分别为37 MPa 和17 MPa.实验测得的应力-应变曲线如图3 所示,砂岩样品在此应力条件下的峰值强度为89.5 MPa,样品的应力-应变曲线表现出的软化特性不明显,其应力-应变曲线是应变硬化型的.根据砂岩的 ε1与 σ1-σ3曲线(图4(a)),并对该曲线求导,获得它的一阶导数曲线图(图4(b)),找到一阶导数快速下降点(即 ε1为0.616%,一阶导数为tan59.9333°的点),此点之后样品的应力应变曲线斜率大幅下降,可将此点视为砂岩的弹性极限,弹性极限为58 MPa.

图3 砂岩真三轴应力-应变曲线Fig.3 True triaxial stress-strain curve of sandstone

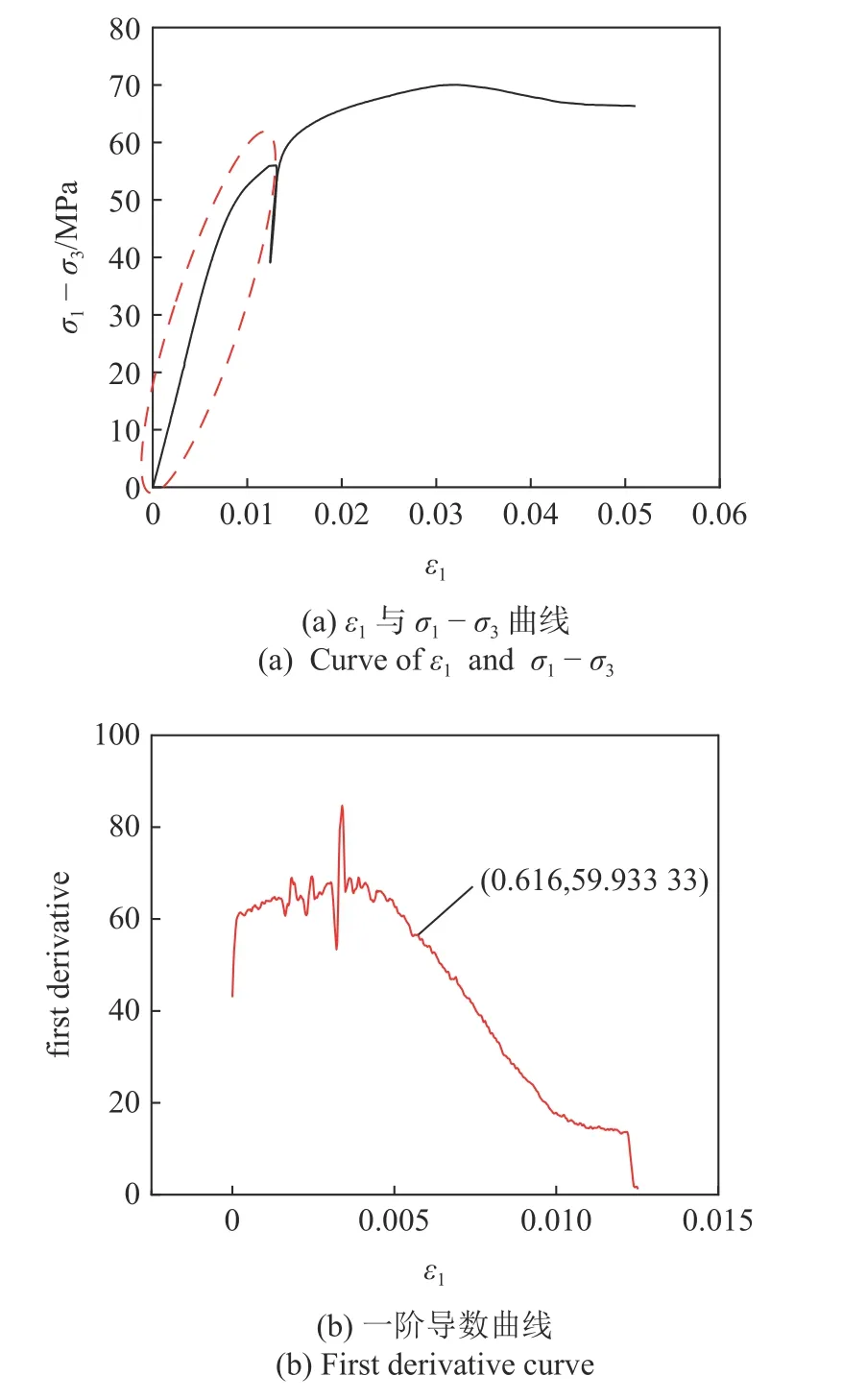
图4 砂岩应力-应变曲线Fig.4 Stress-strain curve of sandstone

1.5 实验方案

本渗流实验施加的总应力依据取样深度(-2465 m)并通过谭成轩[37]提出的经验公式计算得到.地应力随深度变化方程为

式中,H为深度;σmax为最大水平主应力;σmin为最小水平主应力;σv为垂直应力.

计算得到 σmax=58.209 MPa,σmin=38.475 MPa,σv=61.625 MPa.根据S6 储气库工程资料,S6 储气库运行期间储层孔隙压力为8～24.6 MPa,该压力区间是通过地下储气库设计指标和S6 储气库地层条件确定的.当孔隙压力最小时地层有效应力最大,假设有效应力系数为1,由此条件设计了室内渗流实验的最大加载水平 σ1,σ2和 σ3分别为56 MPa,53 MPa 和33 MPa;最小加载水平为 σ1,σ2和 σ3分别为40 MPa,37 MPa 和17 MPa.由于实验设备气体管路所能承受的最大压力为8 MPa,本实验施加的孔隙压力并未根据实际工程条件设置,实验设置的最小孔隙压力为0.4 MPa,最大孔隙压力为6 MPa.

选择具有层理的砂岩样品进行实验,样品视为横向各向同性材料.采用纯度为99.9%的氮气在常温25 °C 下进行实验.同一块岩样进行3 组实验,分别测试样品X,Y,Z3 个方向的渗透率,测试其中一个方向渗透率时,长方体样品另外两个方向用热缩管套进行密封,以防止气体从侧边泄露.应力施加方向、气体渗流方向和层理的关系如图5 所示.

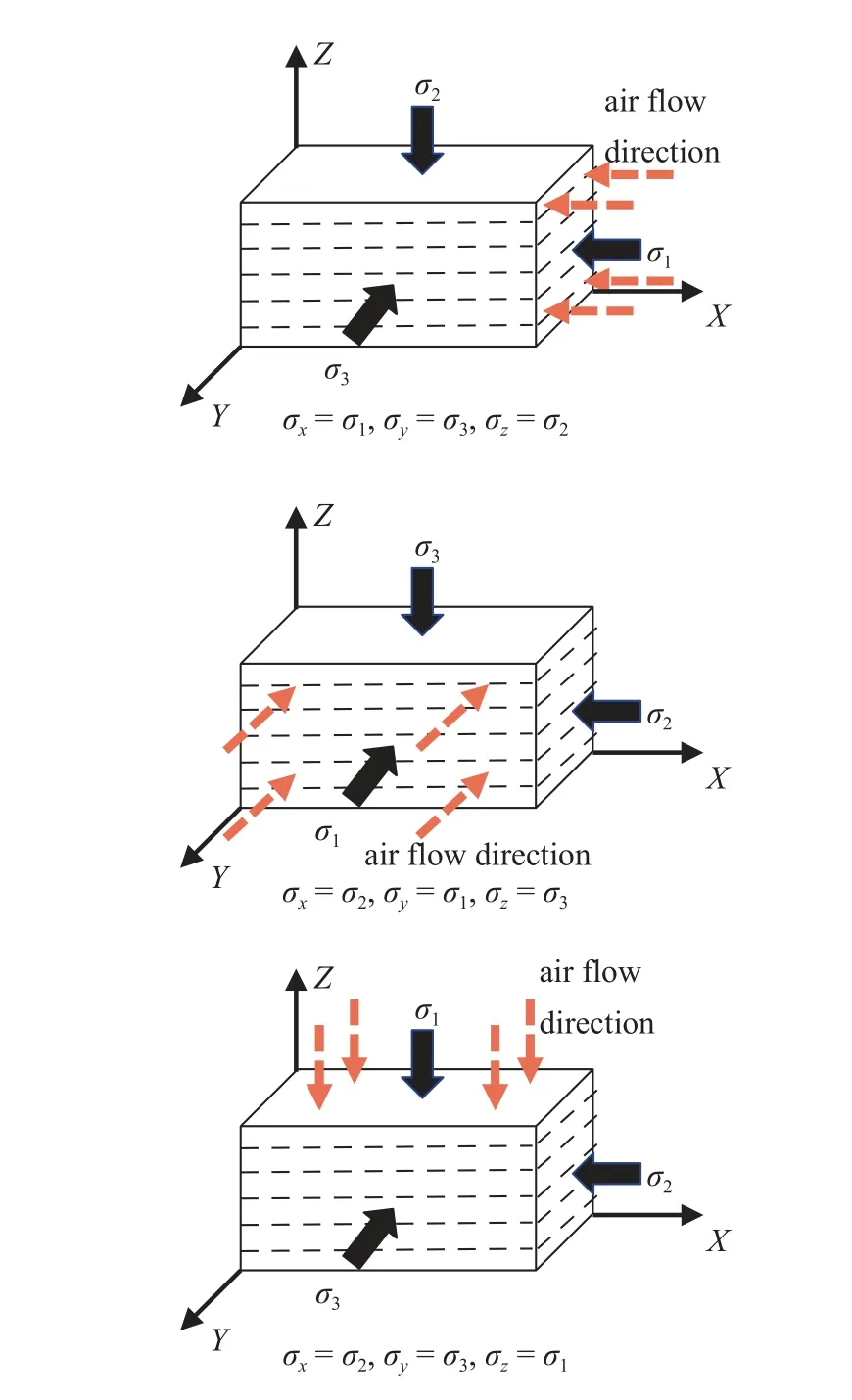
图5 应力加载与层理方位关系图Fig.5 Graph of relationship between stress loading and bedding orientation

每组实验分成3 个阶段: 阶段1 测定岩样的初始渗透率,在静水压力和恒定的孔隙压力下,测量该组渗流方向的渗透率作为岩样在该方向上的初始渗透率;阶段2 研究主应力对渗透率的影响,在真三轴应力状态下,保持孔隙压力恒定,分别单独改变3 个方向的主应力大小,测量该组渗流方向上的渗透率;阶段3 研究孔隙压力对渗透率的影响,在真三轴应力状态下,保持3 个主应力恒定,改变孔隙压力大小,测量该组渗流方向上的渗透率.具体的实验步骤如下.

(1) 静水压力加载: 液压系统压力设置为3 MPa,以0.1 MPa/s 的速率加载,直至各方向应力达到3 MPa 的设置值,3 MPa 的静水压力能防止气体从热缩管套与岩样的接触面泄露.

(2) 打开高压氮气瓶出口阀门,调节上游的减压阀和下游的背压阀,使得上游压力稳定在0.5 MPa,下游压力稳定在0.3 MPa,此时岩样中心孔隙压力约为0.4 MPa,实验中岩样内的孔隙压力视为压力稳定时上下游压力的平均值.待出口流量稳定后,读取流量计读数,计算得到岩样初始渗透率.阶段1 实验完成.

(3) 真三向应力加载: 加载速度为0.1 MPa/s,3 个方向同时进行应力加载,直至各方向应力达到最小加载水平,即 σ1,σ2和σ3分别为40 MPa,37 MPa 和17 MPa 的设置值.首先保持孔隙压力为0.4 MPa 不变,σ2和σ3分别恒定为37 MPa 和17 MPa,σ1从40 MPa 开始增加,每增加4 MPa 测试一次样品渗透率,直至增加到56 MPa,共测量5 次渗透率.然后 σ1和 σ3分别恒定为56 MPa 和17 MPa,σ2从37 MPa 增加到53 MPa,同样每增加4 MPa 测试一次样品渗透率.最后 σ1和 σ2分别恒定为56 MPa 和53 MPa,σ3从17 MPa 增加到33 MPa,同样每增加4 MPa 测试一次样品渗透率,总共测试13 次渗透率.阶段2 实验完成.应力加载路径如图6(a)所示.

图6 渗流实验加载路径Fig.6 Loading path of seepage test

(4) 保持 σ1,σ2和σ3分别恒定为56 MPa,53 MPa 和33 MPa,施加的3 个主应力依据储气库运行期间储层最大的有效应力确定,即 σ1,σ2和 σ3分别恒定为56 MPa,53 MPa 和33 MPa.调节上下游阀门,使孔隙压力从0.4 MPa 依次增加至2 MPa,4 MPa,6 MPa,期间保持样品上下游压差不变,即上下游压力差恒为0.2 MPa.待流量稳定后读取流量计读数,共测试4 次样品渗透率.阶段3 实验完成.应力加载路径如图6(b)所示.

(5) 先卸载气体压力,再卸载主应力.更换气体渗流方向,重新安装热缩管套和样品,重复上述(1)～(4)实验步骤,完成剩余两组渗透率测试实验.

2 实验结果

2.1 岩样初始渗透率

样品渗透率根据公式(1)计算.砂岩中原始的孔隙是气体渗流的主要通道,渗流实验中测试静水压力为3 MPa 时的每个方向的渗透率为该方向的初始渗透率.由实验数据计算得到岩样X,Y,Z3 个方向的初始渗透率见表2.

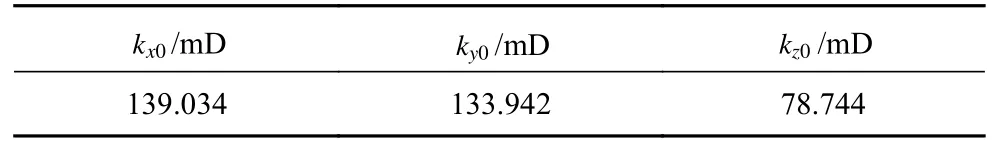
表2 砂岩初始渗透率Table 2 Initial permeability of sandstone

2.2 总应力对岩样渗透率的影响

3 个方向渗透率与施加总应力之间对应关系的具体测试结果详见图7.S6 储气库储层砂岩渗透率很高,由图7 可得出,σ1,σ2和 σ3从40 MPa,37 MPa 和17 MPa 加载至56 MPa,53 MPa 和33 MPa 的过程中,平行层理方向的渗透率kx为100.94～113.98 mD,ky为98.34～111.41 mD,垂直层理方向的渗透率kz为54.98～63.29 mD.样品在X,Y,Z3 个方向上都表现出了随施加的总应力增加渗透率逐渐减小的趋势,整个加载过程储层砂岩的渗透率并没有出现数量级的改变,渗透率随施加总应力连续减小的趋势表明在增压过程中样品内未产生明显裂缝.随着各主应力的增加,砂岩样品内部骨架颗粒之间的孔隙进一步被压缩,样品内部的孔隙和喉道闭合程度提高,渗流通道进一步减少,进而导致渗透率逐步降低.从总体上看,不同应力下渗透率与应力之间服从函数关系.其中,平行层理面方向(X方向和Y方向)的渗透率变化率大于垂直层理面方向(Z方向)的渗透率变化率,但各个主应力引起的两个平行层理面方向的渗透率增量并不相等,垂直于气体流动方向的主应力引起的渗透率增量大于与气体流动方向相同的主应力引起的渗透率增量.当 σ1从40 MPa 增加到56 MPa,σ3从17 MPa 增加到33 MPa 时,渗透率下降的速度基本保持不变;当 σ2从36 MPa 增加到52 MPa 时,渗透率下降的速度略微减小.在X方向上渗透率随主应力的增加分别下降了2.21%,6.45%和3.18%;在Y方向上渗透率随主应力的增加分别下降了2.11%,3.40% 和6.65%;在Z方向上渗透率随主应力的增加分别下降了2.38%,5.49% 和5.85%.

图7 砂岩渗透率与主应力的关系曲线图Fig.7 Relationship between permeability and principal stress of sandstone

2.3 孔隙压力对岩样渗透率的影响

3 个方向渗透率与孔隙压力之间对应关系的具体测试结果如图8.在施加的主应力相同情况下,孔隙压力越大,砂岩3 个方向渗透率越大,其变化规律为正相关关系.当岩石内部孔隙压力增大时,其喉部逐渐打开,微孔体积也逐渐增大,导致其允许流体通过的能力逐渐变大,此后岩样表现出渗透性的增强.在X方向上渗透率随孔隙压力的增加而增大了3.47 %;在Y方向上渗透率随孔隙压力的增加而增大了4.20 %;在Z方向上渗透率随孔隙压力的增加而增大了3.42 %.3 个方向的渗透率变化率并不相同,其中,平行层理方向的渗透率变化率明显大于垂直层理方向的渗透率变化率.此现象说明了孔隙流体压力对各向异性饱和多孔岩石线弹性响应并不是各向同性的,对于储层砂岩渗透率而言,有效应力和施加应力之间对渗透率的影响的差异不能等同于静水压力对渗透率的影响.

图8 砂岩渗透率与孔隙压力的关系曲线图Fig.8 The relationship between permeability and pore pressure of sandstone

3 分析与讨论

3.1 渗透率各向异性分析

不同流动方向的渗透率比称为渗透率各向异性比(permeability anisotropy ratio),即,当PARij=1时,渗透率为各向同性.

根据实验测得的渗透率数据,分别计算了各主应力和孔隙压力加载全过程的渗透率增量值,渗透率增量值如图9 所示.根据初始渗透率和加载过程的渗透率增量值分别计算了初始渗透率各向异性比,加载主应力引起的增量渗透率各向异性比和加载孔隙压力引起的增量渗透率各向异性比(表3),渗透率各向异性比如图10 所示.根据实验加载过程的渗透率增量和表3 中计算的各向异性比数据,通过分析主应力方向、层理方向和气体渗流方向的关系,可以得到如下结论.

表3 砂岩渗透率各向异性比Table 3 Permeability anisotropy ratio of sandstone

图9 加载全过程岩样三维渗透率增量图Fig.9 Three-dimensional permeability increment map of rock sample during loading process

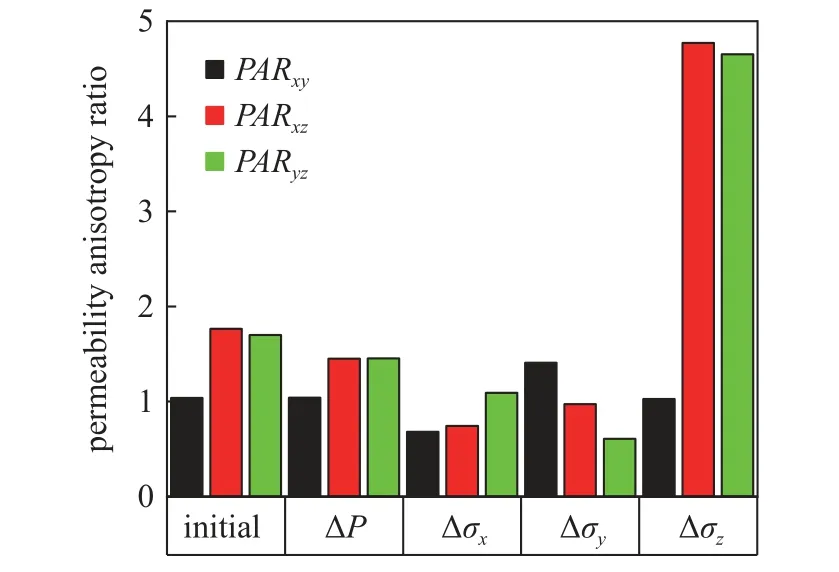
图10 岩样渗透率各向异性比图Fig.10 Permeability anisotropy ratio of rock sample

(1)平行层理方向即X和Y方向的初始渗透率各向异性比为1.038,各向异性比接近1,说明X和Y方向的初始渗透率几乎相等.而平行层理与垂直层理的初始渗透率各向异性比为1.701,说明平行层理与垂直层理方向的初始渗透率存在较强的各向异性.

(2)Z方向应力增量 Δσz引起的渗透率增量中,渗透率增量各向异性比PARxy为1.026,说明σz对XY层理面内的两个渗透率kx和ky的影响几乎相同,同样,孔隙压力对kx和ky的影响也几乎相同;

(3) 应力增量 Δσx和应力增量 Δσy引起的渗透率增量中,渗透率增量各向异性比PARxy分别为0.682和1.409,说明X方向的应力对kx的作用小于对ky的作用,而Y方向的应力对ky的作用小于对kx的作用,即与渗流方向垂直的应力对渗透率的影响大于与渗流方向平行的应力对渗透率的影响.

(4)应力增量 Δσy和应力增量 Δσz引起的渗透率增量中,渗透率增量各向异性比PARxy分别为1.409和1.026,说明Z方向的应力对kx的作用大于Y方向的应力对kx的作用,即与层理垂直的应力对平行层理方向渗透率的影响大于与层理平行的应力对平行层理方向渗透率的影响.

(5)孔隙压力增量 ΔP引起的渗透率增量中,渗透率增量各向异性比PARxy为1.042,而各向异性比PARxz和PARyz分别为1.450 和1.455,说明孔隙压力对kx的作用和对ky的作用几乎相同,但孔隙压力对kx的作用和对ky的作用大于对kz的作用,说明了孔隙流体压力对各向异性饱和多孔岩石线弹性响应并不是各向同性的,孔隙压力对渗透率的作用同样也存在各向异性.

这些计算结果表明,有层理的储层砂岩渗透性各向异性受层理方向的影响较大,这说明储层砂岩层理面方向有利于流体的渗流.而应力方向与渗流方向的关系也对渗透率各向异性有较大的影响,通过分析发现,应力变化引起的砂岩渗透率各向异性最高达到4.771.此外,孔隙压力的作用并不等同于静水压力的作用,孔隙压力也会诱发渗透率各向异性,且诱发的渗透率各向异性主要与层理方向有关.实验结果定量确定了S6 地下储气库储层砂岩渗透率的各向异性程度,并根据不同方向的渗透率计算了渗透率各向异性比.这些结果将更加准确地预测储层渗透率的变化,为地下储气库的储层性能评价提供可靠的技术支持.

3.2 渗透率各向异性机理

分析了岩样垂直层理方向和平行层理方向的铸体薄片图像(图11).由图11 可知,储层砂岩岩石颗粒在垂直层理方向上呈现出明显的中细粒互层现象,具有明显的层状非均质性,而平行层理方向的岩石颗粒粒径则十分均匀.

图11 岩样铸体薄片图(a,b,c 为垂直层理方向铸体薄片图;d,e,f 为平行层理方向铸体薄片图)Fig.11 Thin sections of rock samples (a,b,c are thin sections of cast in vertical bedding direction;d,e,f are cast thin sections in parallel bedding direction)

将储层砂岩的中粗粒层岩石颗粒理想化为直径较大的均匀球体,细粒层岩石颗粒理想化成直径较小的均匀球体,互层均匀排列,如图12(a)所示.岩石渗透率大小主要取决于连通孔隙最小喉道的尺寸.

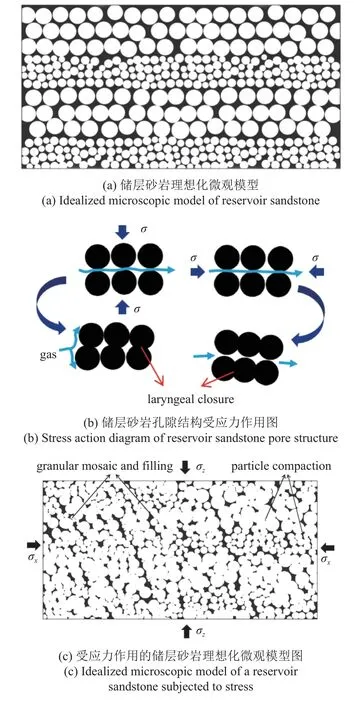
图12 储层砂岩微观模型图Fig.12 Microscopic model of reservoir sandstone

(1)当渗流方向平行于层理时,由于中粗粒层中连通孔隙的喉道尺寸大,对渗透率影响占主要作用,而当渗流方向垂直于层理时,细粒层喉道尺寸小于中粗粒层,渗透率由细粒层喉道尺寸决定.因此平行层理方向的初始渗透率大于垂直层理方向的初始渗透率.

(2)如图12(b)所示,气体在连通的孔隙中流动时,与渗流方向垂直的应力使得渗流方向上的部分喉道封闭,导致该方向的渗透率降低;而当应力与渗流方向平行时,该方向上的喉道大小几乎不受影响,对渗透率的影响较小.这可以解释实验中观察到的与渗流方向垂直的应力对渗透率的影响大于与渗流方向平行的应力对渗透率的影响的现象.

(3)如图12(c)所示,与层理垂直的应力(σz)不仅对岩石颗粒有压实作用,而且会使得细粒层岩石颗粒镶嵌填充中粗粒层的孔隙,导致层理方向连通孔隙的迂曲度增加;而与层理平行的应力(σx)只会对层理的岩石颗粒有压实作用.这能解释实验中观察到的与层理垂直的应力对平行层理方向渗透率的影响大于与层理平行的应力对平行层理方向渗透率的影响的现象.