近场动力学算子方法1)

李志远 黄 丹 Timon Rabczuk

* (河海大学工程力学系,南京 211100)

† (魏玛-包豪斯大学结构力学研究所,德国魏玛 99423)

引言

20 多年来,近场动力学(peridynamics,PD)[1-3]在计算力学与相关工程领域受到了广泛关注.它采用空间积分方程代替经典连续介质力学中的空间微分方程,从而避免了基于连续性假设的传统局部模型在面临不连续问题时的奇异性,在处理诸多工程领域实际问题时表现出较明显优势[4-5],如冲击破坏[6-7]、水力劈裂[8-9]和热力耦合[10-12]等.

PD 模型通常可分为3 类: 键型近场动力学(bond-based peridynamics,BB-PD)、常规态型近场动力学(ordinary state-based peridynamics,OSB-PD)和非常规态型近场动力学(non-ordinary state-based peridynamics,NOSB-PD).BB-PD[1]中物质点间成对的相互作用类似于独立的弹簧,在应用中存在泊松比限制等缺陷.态型PD[2]模型有效地克服了这一限制.当限定泊松比时,OSB-PD 可简化为BB-PD.NOSB-PD 提出关联模型的概念,可重构经典连续介质力学模型,但它受零能模式引起的数值振荡影响[13].为消除振荡,学者们又提出一些处理措施,如附加额外的力状态[13-14]和键关联的近场范围[15]等.对偶域近场动力学[16](dual-horizon Peridynamics,DHPD)的提出则突破了传统PD 模拟中的固定近场范围限制.

基于PD 的非局部作用思想,2016 年Madenci等[17]提出近场动力学微分算子(peridynamic differential operator,PDDO).PDDO 求解偏微分方程(partial differential equations,PDE)是基于强形式,并通过拉格朗日乘子法施加边界条件.2020 年Ren 等[18-19]提出非局部算子方法(nonlocal operator method,NOM).NOM 求解PDE 是基于弱形式,并运用罚能量泛函来抑制零能模式.运用PDDO 和NOM 均可以将PDE 从局部微分形式重构为非局部积分形式.这两类非局部算子近年来均在各种物理学方程求解中得到应用.Li 等[20]提出用于求解PDE 的键关联的PDDO 弱形式,并通过引入键关联的近场范围[15]来消除零能模式.周保良等[21-23]基于PDDO 研究了瞬态热传导[21],正交各向异性热传导[22]以及非线性热传导[23].Li 等[24-27]应用PDDO 分析了复合材料与结构的热弹性[24-25]、动力特性 [26]以及大变形[27].Ren 等[28-30]运用NOM 求解高阶梯度固体[28]、断裂相场[29]与电磁波导[30]等问题.

在PDDO 和NOM 这两类非局部算子的已有研究基础上,本文进一步提出一种更为一般的近场动力学算子方法(peridynamic operator method,PDOM).PDOM 不仅可直接将局部微分转化为相应的非局部积分形式,而且同样适用于微分的乘积.因此,PDDO 和NOM 皆可视为PDOM 的一种特例.以弹性力学问题为例,下文基于变分原理和拉格朗日方程,推导了适用于静/动态弹性力学问题的PDOM 模型,并证明了,当分别限定相互作用域为与位置无关或相关的圆形域时,该PDOM 弹性模型即可简化为通常的PD 或DH-PD 模型.并通过求解3 个典型问题: 杆的拉伸与波动、亥姆霍兹方程和含孔板拉伸问题,说明本方法的准确性、收敛性与稳定性.

1 近场动力学算子方法

考虑定义在M维空间Ω ⊂RM中的标量函数

u(x)∈R,由N阶泰勒展开可得

式中,η=u(x′)-u(x),x′=x+ξ ∈Hx ,Hx为点x的相互作用域,如图1 所示.定义

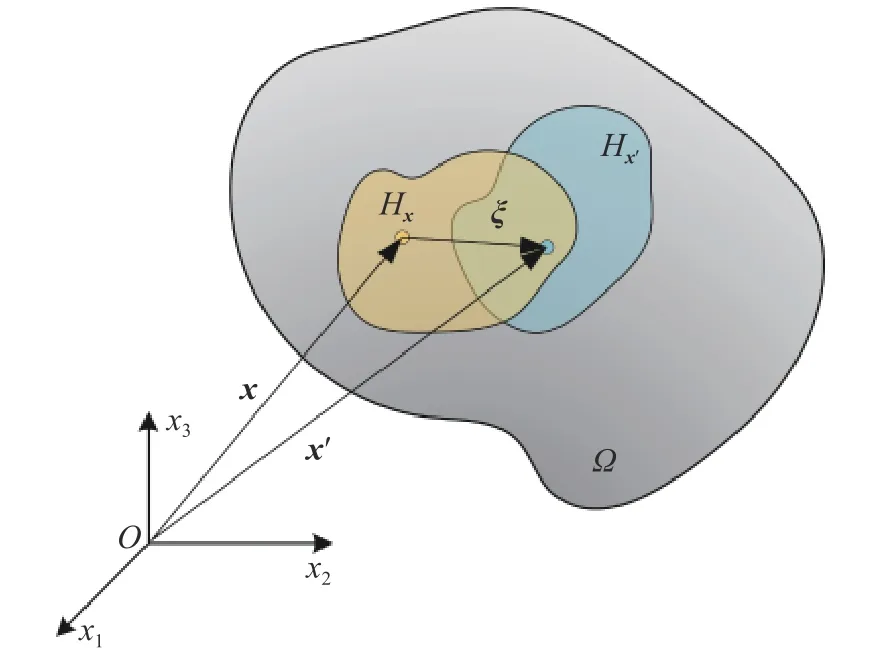
图1 PD 点的相互作用域Fig.1 Interaction domain of PD points

考虑定义在M维空间Ω ⊂RM中的Q阶向量函数u(x)∈RQ,式(1)可扩展为

式中,η=u(x′)-u(x).定义

当Q=1时,式(3)可简化为式(1).

PD 函数构造为

式中,wm为权函数,为待定系数.PD 函数具有正交性

式中,δqipi为克罗内克符号.由式(3)与式(6)可得偏微分乘积的PDOM 构型

将式(5)代入式(6)可得

式(8)可改写为矩阵形式

由式(10)可得待定系数,将其回代式(5),即可确定PD 函数.当Q=1时,PDOM 即可退化为PDDO[17]或NOM[18-19].

接下来,具体给出两种情况的PDOM 构型.

情况 І:M=2,N=1,Q=1

由式(2)可得

将式(11)代入式(4)可得

将式(11)代入式(5)可得

将式(11)和式(12)代入式(7)可得

将式(11)代入式(8)和式(9)可得

情况 П:M=2,N=2,Q=2

由式(2)可得

将式(11)和式(16)代入式(4)得

将式(11)和式(16)代入式(5)可得

将式(11)、式(16)和式(17)代入式(7)可得

将式(11)和式(16)代入式(8)和式(9)可得

2 PDOM 弹性模型

应用PDOM 可以轻易地直接建立很多物理问题的非局部模型.限于篇幅,本节以二维线弹性固体为例,建立PDOM 弹性模型.

2.1 应变能密度

应变张量可表示为

式中,ui为位移.由式(21)和式(14),可得体应变

由式(21)和式(19)可得

由式(22)和式(24),可得应变能密度

式中,λ和 μ为拉梅常数.

2.2 运动方程

系统的拉格朗日量为

式中,T为系统动能,U为系统势能,可表示为

式中,ρ为密度.拉格朗日方程可表示为

式中,Q(k)为广义力,此处只含体力b(k).

式(22)和式(25a)的离散形式可表示为

式中,η(j)(k)=u(j)-u(k).由式(30)可得

由式(26)、式(28)和式(31)可得

将式(27)、式(28)和式(32)代入式(29)并转换成积分形式可得

2.3 求解方案

式(30)可改写为矩阵形式

其中

式中,N(k)为相互作用域H(k)中的离散点个数.将式(36)代入式(26)可得

针对静力学问题,可根据最小位能原理,建立能量泛函

式中,K为整体刚度矩阵,P为载荷列阵

其中,Ntotal为求解域的总离散点数.

针对动力学问题,可采用中心差分法,构建时间积分

式中,Δt为时间步长.由式(34)和式(43)可得

3 与PD 模型的联系

当相互作用域Hx是由与位置相关的半径 δx所定义的圆形域时,式 (35 a)与DH-PD[16]中的内力密度一致.本文模型即可退化为通常的DH-PD 模型.

当相互作用域Hx是由与位置无关的半径 δ所定义的圆形域时,可得=Hx,式(35a)可表达为

式(45)与PD[1-2]中的内力密度一致,本文模型即可退化为通常的近场动力学模型.下文运用PDOM弹性模型生成常用的OSB-PD 模型.

将w(1,0)=w(0,1)=ω(|ξ|)代入式(15),并考虑圆形作用域的Hx对称性,可得

式(47)与OSB-PD 中的加权体积一致.将式(46)和式(13)代入式(23)可得

将式(48)代入式(22)可得

式(49)与OSB-PD 中的膨胀标量状态[2]一致.

将式(50)和式(18)代入式(25b)可得

将式(51)和式(25a)代入式(26)可得

式(52)与OSB-PD 中的弹性能密度一致.将式(48)和式(51)代入式(35b)可得

式(53)与OSB-PD 中的力矢量状态[2]一致.

4 算例分析

本节以一维杆的拉伸与波动、二维亥姆霍兹方程和含孔板拉伸为例,来说明PDOM 的求解能力.当均匀离散求解域 Ω 时,离散间距为 Δx,采用方形相互作用域

当非均匀离散时,选定N(k)个距离x(k)最近的点组成相互作用域H(k).定义.权函数设定为

式中,nw为权重指数.

4.1 杆的拉伸与波动

一维杆的运动方程可表示为

式中,u为轴向位移,A为截面面积,E为弹性模量.对于静态拉伸问题,不考虑式(56)左端的惯性力.杆的左端固定,右端受到轴向力P作用.边界条件可表示为

拉伸问题的精确解为

对于动态波动问题,设置式(58)为初始位移,初速度为零.边界条件和初始条件可表示为

波动问题的解析解为

该问题的能量泛函为

根据Q=1,2情况的PDOM,可构造

通过拉格朗日方程,式(56)可改写为

对于杆的拉伸问题,相关参数设定为EA=1,P=1,nw=3,N=2(Q=2时),N=1(Q=1时).

图2 给出Q=1,2,m=2,3,Δx=0.02时杆拉伸的位移误差对比.可以看出Q=1时的结果(此时得到的就是没有引入其他额外的数值振荡消除方法时的PDDO 或NOM 结果)有明显的由零能模式引起的数值振荡,而Q=2时的PDOM 结果非常稳定.这表明本文方法可以从根本上有效避免零能模式.

图3 给出Q=2,m=2,3,Δx=0.005,0.01,0.02和0.05 时杆拉伸的全局误差收敛.收敛率分别为r=1.0301,1.1568,说明本方法具有良好的收敛性.其中,全局误差由L2 范数衡量

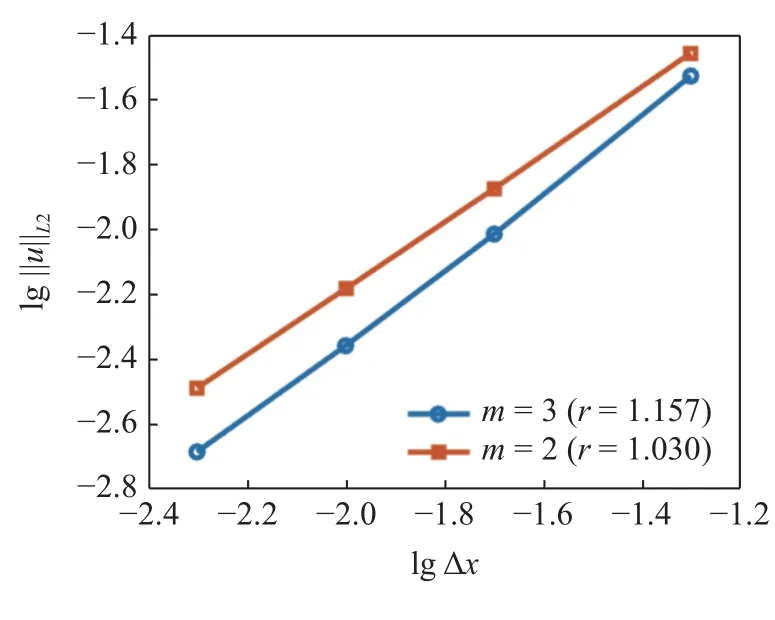
图3 杆拉伸的全局误差收敛Fig.3 Convergence of global error for bar tension

对于杆的波动问题,相关参数设定为 ρ=1,Δt=1.0×10-4,Δx=0.01,m=3.图4 给出杆波动的位移时空分布.图5 给出杆波动的位移分布对比.从图中可以看出,PDOM 结果与精确解吻合良好.结果表明本方法可以高精度求解一维稳态与瞬态问题.

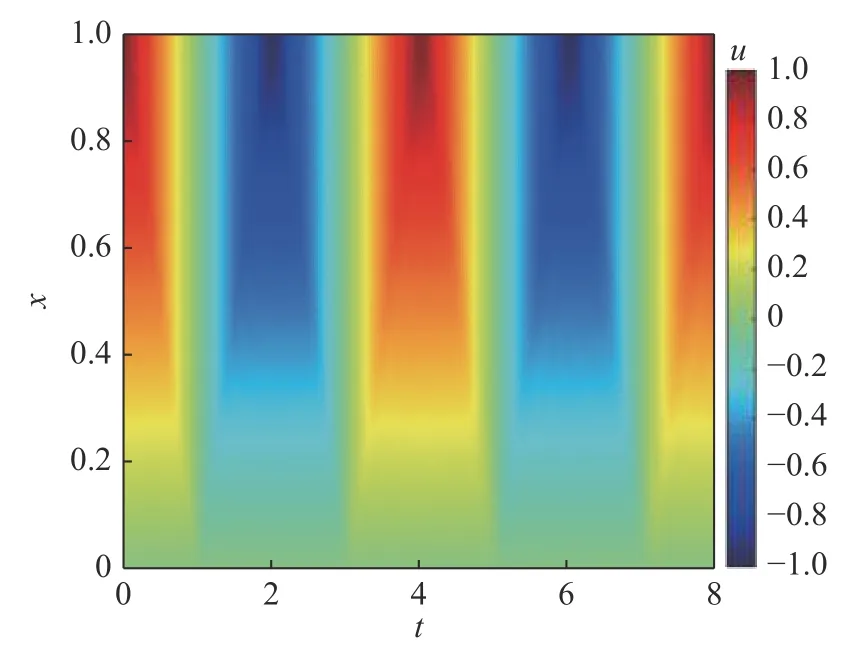
图4 杆波动的位移时空分布Fig.4 Displacement in space and time for bar wave

图5 杆波动的位移分布对比Fig.5 Comparisons of displacement for bar wave

4.2 亥姆霍兹方程

二维亥姆霍兹方程可表达为

式中,k为波数.精确解为

式中,J0是第一类零阶贝塞尔函数

根据精确解,求解域四边施加狄利克雷边界条件.

该问题的能量泛函为

根据Q=2情况的PDOM,可构造

将相关参数设定为m=3,nw=6,N=2,Δx=0.01.图6 给出不同波数情况下亥姆霍兹方程的PDOM位移结果分布.图7 给出不同波数情况下亥姆霍兹方程在 0 ≤x1≤1,x2=0上的位移分布对比.可以看出,PDOM 结果与精确解完全重合.表明了本方法求解二维问题的能力.

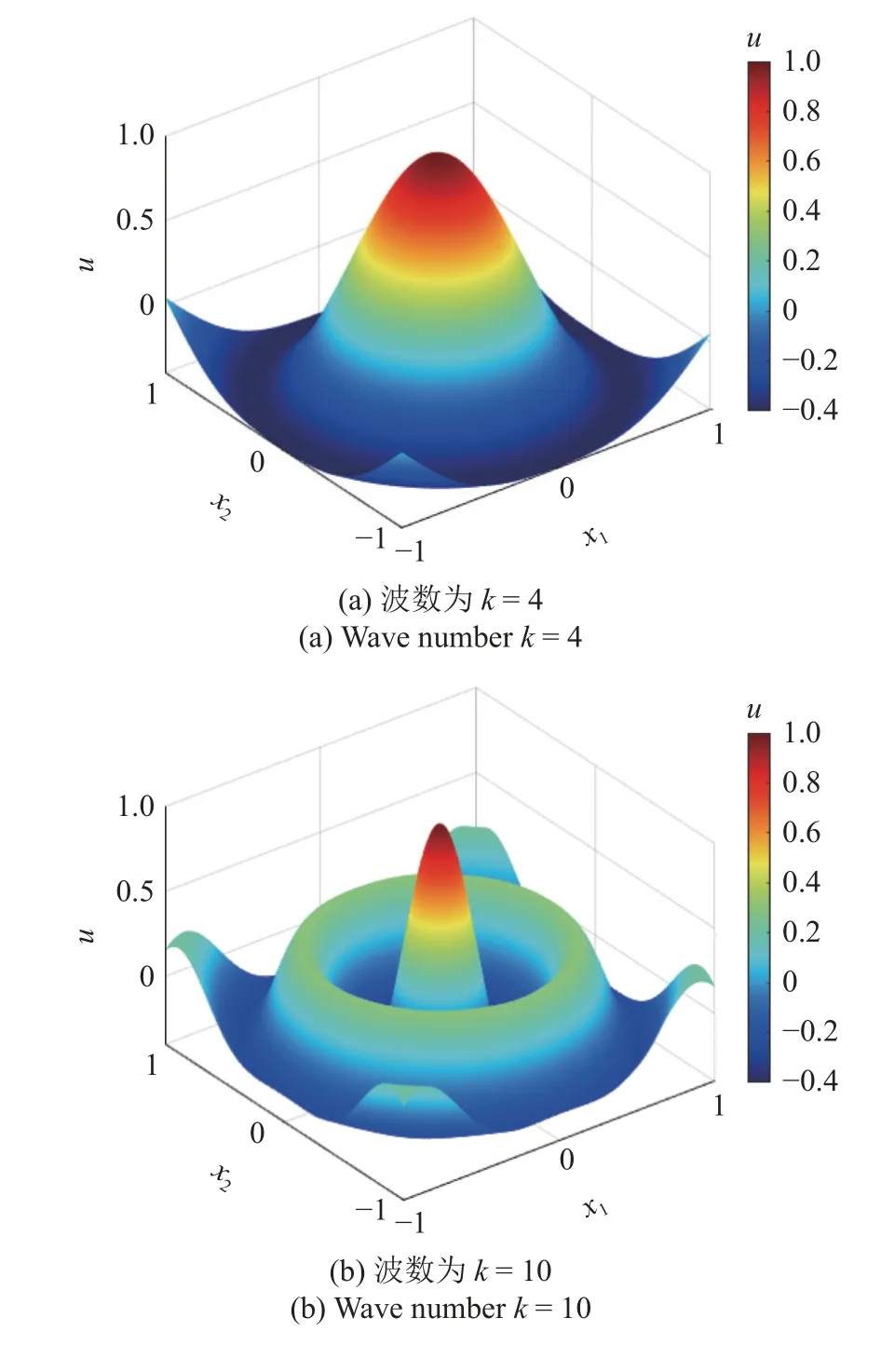
图6 亥姆霍兹方程的PDOM 位移分布Fig.6 PDOM displacement for Helmholtz equation

图7 亥姆霍兹方程的位移分布对比Fig.7 Comparisons of displacement for Helmholtz equation

4.3 含孔板拉伸

考虑均质无限大的含孔板拉伸,如图8(a)所示,P为拉伸均布力,a为圆孔半径.该问题精确解为

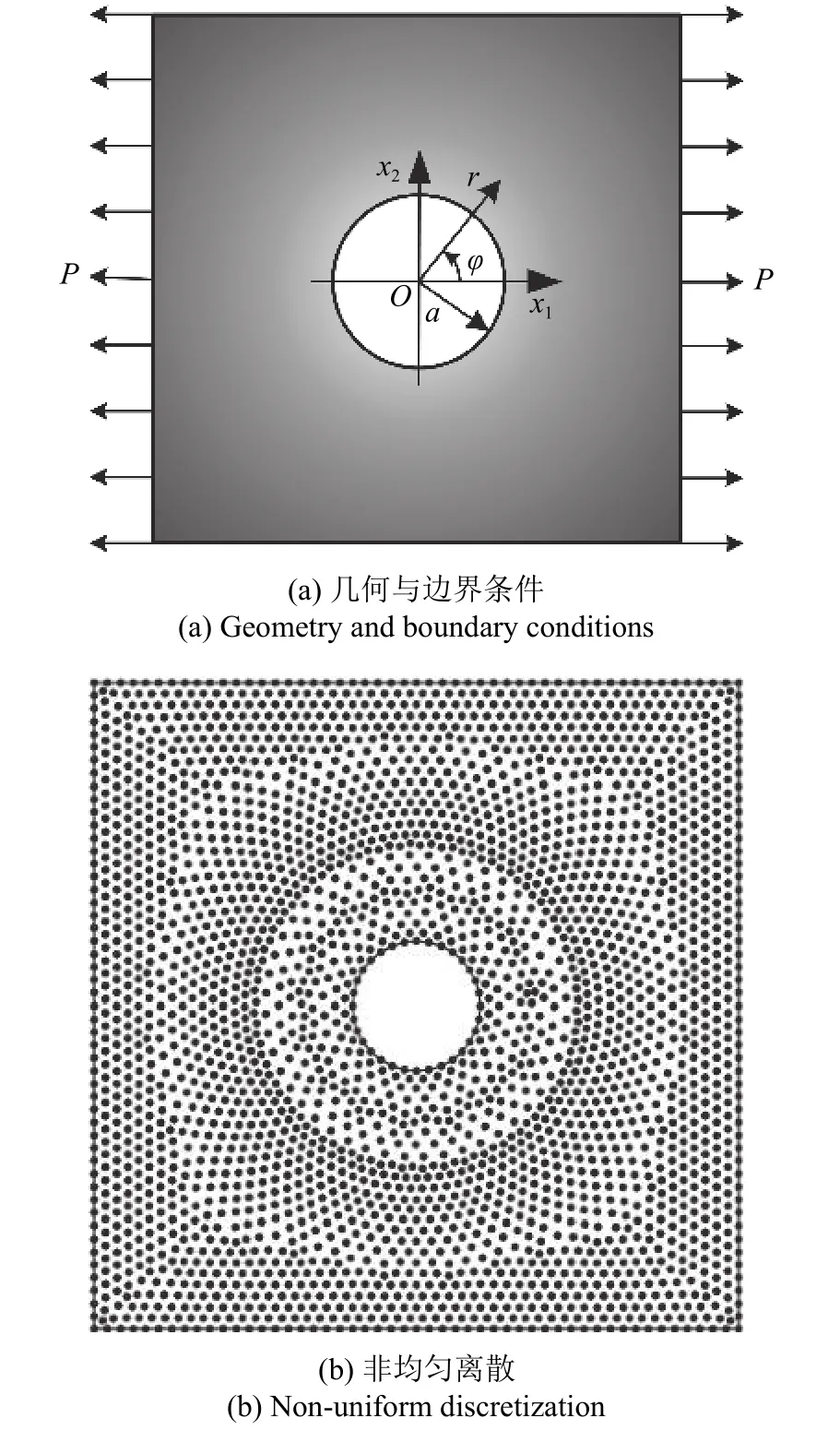
图8 均质含孔板拉伸Fig.8 Homogeneous plate with a hole in tension

式中,r和 φ分别为极坐标系极径和极角,κ为体积模量,σφ为环向应力.

设定方板边长为1,圆孔半径a=0.1,非均匀离散11152 个点,如图8(b)所示.弹性模量取1000,泊松比取0.3,均布力取P=1.根据精确解施加狄利克雷边界条件.

相关参数设定为nw=6,N=2,N(k)=25.图9给出含孔板拉伸的PDOM 位移结果分布.图10给出含孔板拉伸在r=0.3上的位移与应力分布对比.可以看出,PDOM 结果与精确解完全一致,表明本方法在非均匀离散情况下依然可以保证高精度.

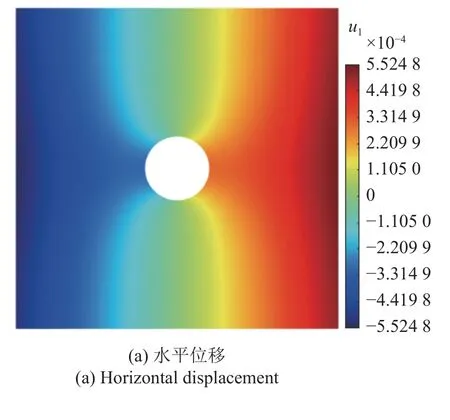
图9 含孔板拉伸的PDOM 位移分布Fig.9 PDOM displacement for plate with a hole in tension

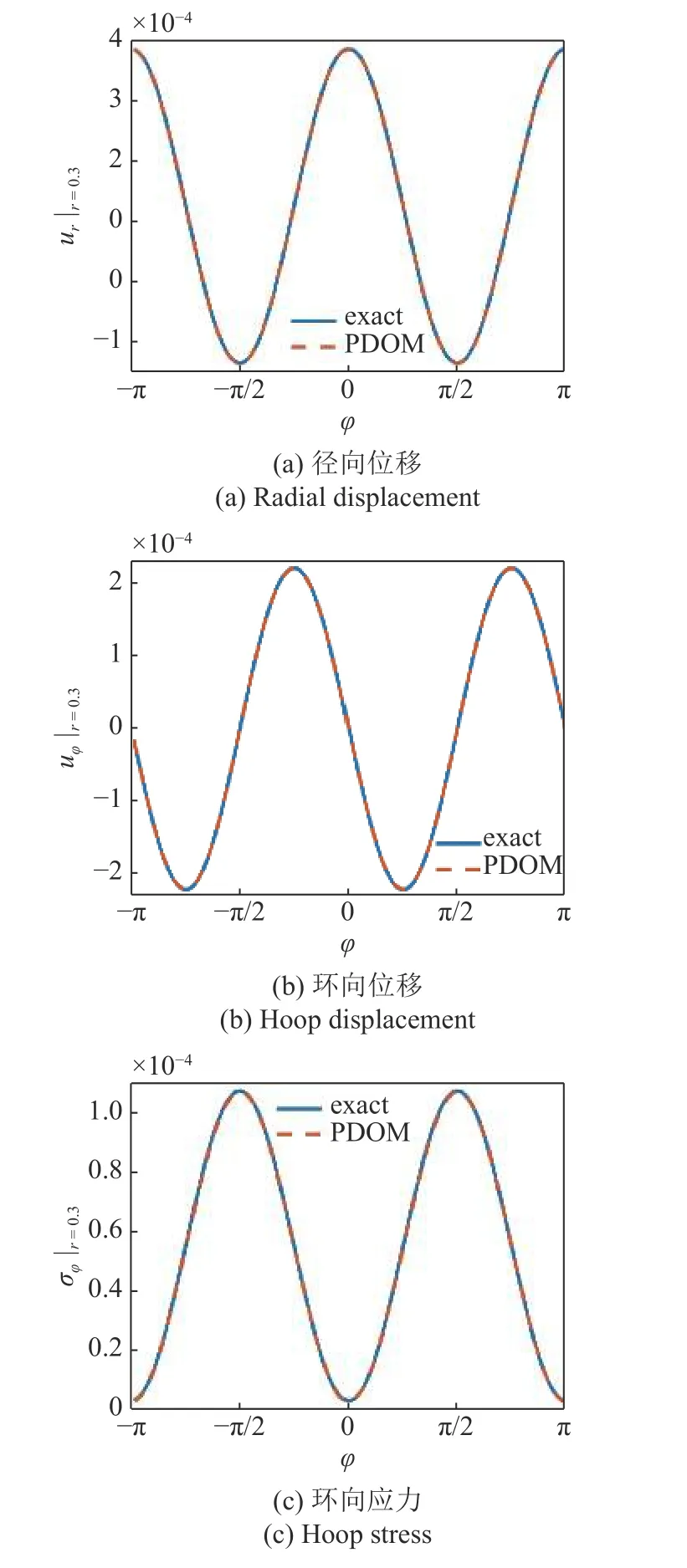
图10 含孔板拉伸的位移与应力分布对比Fig.10 Comparisons of displacement and stress for plate with a hole in tension

5 结论

本文提出一种基于非局部思想求解物理学问题的方法,称之为“近场动力学算子方法”.给出了理论推导过程,与已有方法和模型进行了对比,并以弹性力学问题为例,运用变分原理和拉格朗日方程,建立了适用于静/动态弹性力学问题的PDOM 弹性模型,通过几个典型算例进行了验证.本文得出主要结论如下.

(1) PDOM 可将任意阶局部微分及其乘积转化为相应的非局部积分形式.当Q=1时,PDOM 可退化为目前两种受到关注的求解微分方程的非局部算子: PDDO 或NOM.

(2) 当相互作用域取为与位置无关的半径 δ或相关的半径 δx所定义的圆形域时,PDOM 弹性模型即可简化为通常的PD 或DH-PD 模型.

(3) 通过求解杆的拉伸与波动、亥姆霍兹方程和含孔板拉伸3 个经典问题,表明本方法具有良好的计算精度、收敛性和数值稳定性,能有效避免零能模式,且适用于非均匀离散.

PDOM 方法可为基于非局部思想求解微分方程组、分析不连续问题提供一种选择.本文受篇幅限制,仅给出理论部分并以二维弹性力学问题为例开展了相关建模过程演示和分析.特别欢迎和期待相关领域广大同仁采用PDOM 方法求解其他各种问题,特别是不连续问题.