通过“不同类量的比”实现概念延展
2023-08-05魏先玲许佳敏张维国巩子坤
魏先玲 许佳敏 张维国 巩子坤


摘 要:比的概念从“同类量的比”发展到“无量纲的数的比”的过程中,需要“不同类量的比”作为关键的跳板。正是因为现实生活中的存在性、数学知识中的必要性,“不同类量的比”的学习才显得如此重要。“不同类量的比”的教学,可借助除法和倍数关系认识比的本质,实现从同类量比到不同类量比的过渡;设计符合学生思维层次的、具有螺旋上升性的问题,激发学生学习的内驱力,引领学生探究数学本质。
关键词:小学数学;比的认识;不同类量的比;概念延展
本文系浙江省哲学社会科学规划课题“基于认知发展模型的义务教育教科书编写质量提升研究”(编号:23NDJC265YB)、浙江省高校重大人文社科攻关计划资助项目“建设高质量教育体系背景下义务教育教科书编写质量提升路径研究”(编号:2023GH005)的阶段性研究成果。巩子坤为本文通讯作者。
两个数相除,又叫作两个数的比——这是目前教材中对“比”的定义。然而,比不等于除法:比的本质是倍数关系,描述的是两个量之间的一种状态,一种对比;除法表示一种运算,比只是在求比值时才用除法[1]。比原本是同类量的倍数关系,但是也可以推广到不同类量的情形,即不同类量a、b,以b为单位衡量a,也称a和b之间有关系a比b,记作a∶b。两者最显著的差异就在于量纲:同类量的比,其比值是无量纲的;而不同类量的比,比的前后项里的量纲不能约去。[2]
那么,为什么要学习不同类量的比呢?正如上段提到的,不同类量的比就是以一个量为单位来衡量另一个量,而这在现实生活中十分常见,如每小时行驶多少千米、每本书多少元、每分钟出水多少升等,它们本质上就是不同类量的比。其次,比的概念从“同类量的比”发展到“无量纲的数的比”的过程中,需要“不同类量的比”作为关键的跳板。正是因为现实生活中的存在性、数学知识中的必要性,“不同类量的比”的学习才显得如此重要。
在“同类量的比”学习结束后,我们对班里低、中、高三个层次共15名学生做了访谈,请学生举例说一说什么是不同类量的比。其中,3名学生能够正确举例,12名学生举出了错误的例子,如“直径与半径的比是不同类量的比”。分析访谈结果,发现大部分学生不理解不同类量比的概念,无法自行从同类量的比过渡到不同类量的比。因此,我们尝试构建并优化“不同类量的比”的学习路径,实现学生从“同类量的比”到“不同类量的比”的过渡。
基于上述思考,提出两个研究问题:(1)如何设计一条“不同类量的比”的学习路径,即设计一条能够促进学生对“不同类量的比”的认识从简单到复杂、从低级到高级的学习路径;(2)在学习路径的推进中,如何促进学生由“同类量的比”过渡到“不同类量的比”,并进一步体会比的本质。具体研究如下:
一、研究设计
研究对象是深圳市一所普通小学六年级甲、乙两个平行班(与开展“同类量的比”教学实验的班级相同)的学生。由教师W授课。研究方法与流程同“同类量的比”教学实验,本文不再赘述。
这里,主要介绍后测问卷及数据处理。
后测问卷中,有这样3道题:
1.小明跑36 km需要2小时,路程与时间的比是( ),比值是( ),这个比值表示( )。
2.400 g大豆榨油48 g,油与大豆的质量比是( ),比值是( ),这个比值表示( )。
3.以上两道题,第( )题描述的是同类量的比,第( )题描述的是不同类量的比。
每一空,回答正确计1分,回答错误或没有回答计0分。
二、研究过程与分析
(一)学习路径B1
1.任务介绍
学习路径B1围绕“比”的两种不同形式,即同类量的比和不同类量的比,重点关注从同类量的比到不同类量的比的过渡。
设计了5项任务:
任务1的目标:课前分享,为后续学习不同类量的比做好铺垫。子任务1:“8”字长绳比赛中,我班有7名男生,6名女生,男生与女生的人数比是( )。子任务2:跳远比赛中,小红跳了5米,小丽跳了4米,小红与小丽跳远的长度比是( )。在这两项子任务中,学生复习巩固了同类量的比的概念——像这种,人数与人数的比、长度与长度的比,当比中的两个量都是同一类量时,我们就称其为同类量的比。
任务2的目标:感知速度就是单位时间内所走的路程,体会比的度量含义。子任务1:小辉跑200米用了8秒,路程与时间的比是( ),速度是( )。子任务2:8米/秒表示什么意思?4秒时,路程是多少?这里,沿用了“同类量的比”教学的运动会情境,使得教学情境一以贯之,学生不会有明显的脱节感。学生通过写一写、填一填“路程与时间的比”,体会不同类量比的含义;通过说一说“8米/秒”的含义等,体会通过路程与时间这两个不同类量的比,得到了一个具有相对意义的量(衍生的量)——速度。最后,教师总结:当两个量的单位不同时,如路程与时间,我们就称它们的比为不同类量的比;当两个不同类量相比时,就会产生一个新的量。
任务3的目标:根据“总价与数量的比”,进一步理解、感悟不同类量比的含义。子任务1:老师买了2本笔记本花了12元,写一写总价与数量的比是什么,单价是多少,单价表示什么意思。子任务2:这里的比是哪一种比呢?你还发现了什么?任务3转换情境,呈现总价与数量这对不同类量的比,通过这对不同类量的比,得到又一个具有相对意义的量——单价。学生通过填写学习单,说一说单价的含义,并区分这是哪一种比。情境的转换,使学生巩固对不同类量比的认识与理解。
任务4的目标:实现数学从生活中来,到生活中去。具体内容是:“说一说生活中,你还知道哪些不同类量的比。”这一任务,让学生自己举例,结合生活实際,说一说在生活中还有哪些不同类量的比。这使得学生进一步巩固对不同类量比的理解,学会用数学的眼光观察现实世界,体会到现实生活中处处有数学。
任务5的目标:比较、分析、判断同类量比和不同类量比的联系和区别。具体内容是:“仔细观察同类量的比和不同类量的比,想一想:它们有什么相同点?有什么不同点?”通过让学生分析任务1中的同类量比和任务2、任务3中的不同类量比的异同,体会两者之间的联系与区别:同类量比的两个量单位相同,不同类量比的两个量单位不同;但两者都可以表示两个量之间的倍数关系,都可以写成两个数相除。通过这样的比较分析活动,帮助学生进一步加深对两者的理解。
2.问题分析
(1)没有“比较”,无法深刻体会不同类量比的度量含义
任务2与任务3利用了速度模型与单价模型,引导学生通过“路程与时间”“总价与数量”这两对不同类量的比,得到两个新的量——速度与单价。但这样只举一对“路程与时间”或“总价与数量”数据的方式,没有比较“谁跑得快”“哪一本贵”的问题驱动,无法凸显“速度”与“单价”出现的必要性,学生也无法深刻体会不同类量比的度量含义。
(2)情境不同,无法较好地凸显两类比的差异与比的本质
任务5中,教师让学生比较任务1中同类量的比与任务2、任务3中不同类量的比,体会两者的异同,通过相同点进一步感受比的本质是表示两个量之间的倍数关系。然而,由于两类比本身存在的情境有较大的差异性,因此学生在比较时容易被非关键因素影响,无法较顺利地指出两者的异同,更无法深刻体会比的本质。
(3)从同类量比到不同类量比的过渡并不充分,学生对不同类量比的概念理解并不完全
同类量的比、不同类量的比这两个概念都是教师直接告知学生的,学生主动获取知识的动力不足。学生没有经历充分的观察、对比、判断、分析等一系列学习体验活动,从同类量比过渡到不同类量比的过程并不自然,所以学习感触不深,对不同类量比的概念建构仍不完全。
3.修改建议
(1)利用“比较”,充分体现不同类量比的度量含义
增加更多“路程与时间”“总价与数量”的数据,设置“谁跑得更快”“哪一本更贵”的驱动问题,引导学生为解决上述问题,自发计算两个不同类量的比值,由此体会到不同类量比的度量含义。
(2)在同一情境中比较同类量的比和不同类量的比
利用更多的“路程和时间”数据,引导学生从中得到不同路程之间的比、不同时间之间的比。由此,在同一情境中同时呈现同类量的比和不同类量的比,情境的统一更有利于学生认识到两者的异同,体会比的本质。
(3)层层递进,引领学生从同类量的比过渡到不同类量的比
从复习旧知入手,唤醒学生对同类量比的理解;在具体的情境中,如“谁跑得更快”这样的情境中,引导学生使用不同类量的比,体会不同类量比的度量意义;通过比较“同类量的比”和“不同类量的比”,引导学生对两个概念进行归纳、概括、命名,在辨析中加深对不同类量比的理解;在新情境中,继续应用不同类量的比,进一步感悟不同类量的比。由此,引导学生经历概念的发生、发展过程,从“同类量的比”逐步过渡到“不同类量的比”,理解不同类量比的含义。
(二)学习路径B2
1.任务介绍
经过对学习路径B1的课后反思与讨论,教师修改教学设计,在乙班实施了学习路径B2。
设计了5项任务:
任务1的目标
与内容同学习路径B1中的任务1。
任务2的目标:初步探究,借助速度模型体会不同类量比的含义,适时渗透函数思想。子任务1:小辉跑50米用了10秒,小红跑200米用了40秒,谁跑得快呢?写一写,算一算。子任务2:横着看,路程与时间相比,产生了一个新量,是什么?什么变了,什么没变?子任务3:竖着看,请仔细观察,你发现了什么?任务2以速度模型为例,在“谁跑得更快”的问题驱动下,引导学生初步感知两个不同类量相比会产生一个新的量,感受不同类量比的度量含义;通过“横向”与“纵向”的比较,在同一情境中同时呈现同类量的比和不同类量的比,为后续两者的比较做铺垫;
同时,体会速度不变时,路程随时间的变化关系,渗透函数思想。
以下是课堂实录片段:
师 路程除以时间,可以用比的形式来表示吗?
生 可以,200除以40可以写成200∶40,50除以10可以写成50∶10。
师 当路程和时间相比,就会得到……
生 (齐)速度。
师 在这里,速度表示什么意思呢?
生 速度就是每秒钟跑的路程。
师 路程与时间相比就得到了——速度。有了速度,我们就可以进行比较,就知道谁快谁慢。刚刚是横着看,我们还可以怎样看?怎样比?
生 还可以竖着看,200是50的4倍,40是10的4倍,都是4倍,所以一樣快。
师 能用比表示吗?
生 50∶200。
生 10∶40。
任务3的目标:沟通联系,打通同类量的比和不同类量的比之间的壁垒。
具体内容是:仔细观察黑板左边的比和右边的比,有什么相同点,有什么不同点?
这项任务中,教师引导学生观察黑板左边的比(见下页图1)和右边的比(见下页图2),并分析两者的异同。学生通过分析、比较,发现两者的不同点在于“左边的比”是路程比时间,单位不同;“右边的比”是路程比路程,时间比时间,单位相同。于是,根据两者的特点,分别将两者命名为“不同类量的比”和“同类量的比”。在分析相同点时,教师引导学生发现两者都可以表示成一种倍数关系,并且其倍数关系可以通过除法计算得到具体的数值(比值)。通过将同类量的比与不同类量的比进行比较,打通知识间的壁垒,实现从同类量比到不同类量比的过渡。
以下是课堂实录片段:
师 仔细观察黑板(如图3、图4所示),左边的比与右边的比,两者有什么相同点?
(学生思考。)
师 我们知道,同类量的比可以看作两个量之间的倍数关系,如我花费的时间是你的4倍,我走的路程是你的4倍。那么,不同类量的比是否也可以看作倍数关系呢?
生 10秒跑了50米,50米平均分到10秒内,每秒就跑了5米,50是10的5倍,所以也可以看作倍数关系。
师 同类量的比和不同类量的比都可以表示成倍数关系,那么具体是多少倍呢?我们可以怎么算?
生 (齐)用除法。
任务4的目标:感悟本质,借助单价模型进一步感悟不同类量的比。子任务1:老师想买笔记本奖励小辉和小红,哪一种笔记本最贵?子任务2:总价与数量相比得到一个新的量,是什么?表示什么意思?写一写,说一说。子任务3:你能用倍数关系来解释总价与数量之比嗎?任务4借助单价模型,在“哪一种笔记本最贵”的问题驱动下,引导学生进一步体会不同类量比的度量含义,并巩固对比的本质的理解。
以下是课堂实录片段:
师 哪一种笔记本最贵?你是如何得到这个答案的?
生 B种笔记本最贵,我将总价与数量相比,计算并比较它们的比值。
师 总价与数量相比会产生一个新的量,它是什么,有什么含义?
生 产生的新的量是单价,表示1本笔记本的价钱。
师 你能用倍数关系来解释总价与数量之比吗?
生 以B种笔记本为例,15元买了3本,15元平均分到3本里,每本就是5元,15是3的5倍。
任务5的目标:深化含义,寻找生活中不同类量的比。具体内容是:
速度是路程与时间的比,单价是总价与数量的比,生活中还有这样的比吗?这项任务联系生活实际,唤醒学生关于不同类量比的经验,引导他们体会现实生活中处处有数学。
2.教学效果
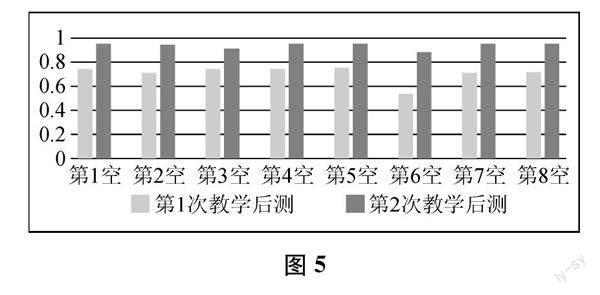
将两次后测数据进行比较(见下页图5),发现乙班学生在每一空上的平均得分均高于甲班。分别对甲、乙班学生8个空的得分进行独立样本t检验,结果表明,甲、乙班在每个空上的得分均存在显著性差异(p<0.05)。这说明,学习路径B2的教学,让学生对比的含义的理解有了明显提升,对什么是同类量的比、什么是不同类量的比也有了深刻的认识和理解。这与课堂上教师创设适切的对话问题、创设生生互动与师生互动的平台、创设整体的教学情境关系密切。
课后,对低、中、高三个层次各3名学生进行访谈,发现8名学生能够理解比表示两个量之间的倍数关系,7名学生能够正确列举生活中同类量的比和不同类量的比,所有学生都能够说出具体情境下比的含义,这一结果与后测的数据吻合。这一系列数据和现象都证明,改进后的学习路径得到了优化,提高了课堂教学的实效性,有助于学生从同类量的比过渡到不同类量的比,加深对比的本质的认识。
三、研究结论与建议
(一)结论
本研究探索了有利于学生理解不同类量比的学习路径,实现了从同类量比到不同类量比的过渡,拓展了比的含义。
首先,从分享旧知入手,巩固上节课学习的同类量的比,为后续学习不同类量的比做铺垫;接着,借助速度模型,深入体会不同类量比的含义,适时渗透函数思想;分析、感悟同类量的比与不同类量的比之间的异同,打通两者之间的壁垒;借助单价模型进一步感悟不同类量的比的本质;最后,通过寻找生活中不同类量的比,深化对比的含义的理解。
在分析同类量比与不同类量比的异同时,引导学生体会两者的不同点在于相比的两个量的单位是否相同;而相同点在于都表示两个量之间的倍数关系,并且都可以用除法计算得到具体的倍数关系(比值)。
(二)建议
1.借助除法和倍数关系认识比的本质,实现从同类量比到不同类量比的过渡比的本质是两个量之间的倍数关系,而除法是两个量之间倍数关系的另一种表达方式,与比存在联系。教学中,教师可以通过同类量比和不同类量比的比较,引导学生发现比的本质是两个量之间的倍数关系;通过除法来计算两个量之间的倍数关系(相应比的比值),引导学生发现比与除法存在联系。由此,发现同类量比和不同类量比的一致性,结合两者的不同之处,实现从前者到后者的过渡。
2.设计符合学生思维层次的、具有螺旋上升性的问题,激发学生学习的内驱力,引领学生探究数学本质学习的发生不是“一厢情愿”,而是“两拍即合”。教师设计的所有教学活动要符合学生的认知层次,在学生的“最近发展区”内。例如,在引导学生从同类量的比过渡到不同类量的比时,开展层层递进的对话。只有让学生体验获取成功的喜悦和快乐,学生才能激发学习的欲望,才会产生探究知识的内在需求,从而促进教学活动深入开展。
参考文献:
[1][2] 张奠宙,巩子坤,任敏龙,等.小学数学教材中的大道理——核心概念的理解与呈现[M].上海:上海教育出版社,2018:173,175.
