一种改进的浸入运动边界算法
2023-08-03付少童贾龙菲王利民
付少童,贾龙菲,王利民,*
(1.中国科学院 过程工程研究所 多相复杂系统国家重点实验室,北京 100190;2.中国科学院大学 化学工程学院,北京 100049;3.沈阳化工大学 化学工程学院,沈阳 110142)
0 引言
气固多相流系统广泛存在于自然界和工业过程,自然界中如河流过障、泥石流、尘埃悬浮等,工业过程中如飞机获得升力、桥梁振动、循环流化床反应器等均涉及复杂的流固耦合运动。流体与固体间相互作用为非线性的多物理现象[1],体系的复杂性远超单相流问题,如何准确解析移动的流固边界是正确处理流固耦合的关键。
近年来,格子Boltzmann 方法[2](lattice Boltzmann method,LBM)发展较为迅速,其属于介于宏观连续介质模型和微观分子动力学模型之间的介观模型,物理背景清晰;相较于有限差分法、有限体积法、有限元法等常规的计算流体力学方法,LBM 具有求解简单、容易并行等特点,受到国内外学者的广泛关注。目前基于LBM 研究者们构建了多种描述移动边界的方法,如边界链法(link-bounce-back,LBB)、干颗粒耦合法(dry particle coupling method,DPC)和浸入边界法(immersed boundary method,IBM)等。LBB 由Ladd等[3]提出,其将边界视为阶梯状的球壳,并应用于多颗粒沉降问题,但模拟边界与物理边界存在偏差。DPC 法[4]中内部不再保留流体格点,即内部不存在流体的惯性力,但需要频繁生成和删除格点,且无法保证局部质量守恒。IBM 最早由Peskin[5]提出,固体边界由一系列拉格朗日点描述,通过插值函数实现流体点与一系列固体边界点的相互作用。
Nobel 等[6]提出了一种LBM 框架下处理运动固体边界的方法,即浸入运动边界法(immersed moving boundary,IMB),其引入格子控制体和格子固含率描述边界,通过固含率实现流体到固体的平滑过渡,而权重系数作为固含率的函数用于分配流体碰撞算子和固体碰撞算子的作用比重。Cook 等[7]将IMB 与DEM 方法耦合,进一步考虑固体间相互作用。Chen等[8]验证该方法对运动边界的处理是完全有效的。Feng 等[9]在此基础上引入大涡模拟(large eddy simulation,LES)对高雷诺数颗粒流体系统进行模拟。Wang 等[10]将该方法与时间驱动硬球模型(timedriven hard-sphere,TDHS)相结合,成功复现了流化床中颗粒散式流态化和聚式流态化现象。此外,该方法还被应用于处理变形凝胶输运[11]、黏性固体流动[12]以及水力压裂[13]等问题。Xiong 等[14]基于该方法开展了129 024 个颗粒流动计算。Zhou 等[15]基于大规模气固系统的直接模拟发现经典的Wen &Yu阻力公式预测值偏高且方向存在偏差。Liu 等[16-17]对4.83 × 109个流体网格和115 200 个固体颗粒的周期悬浮进行了直接数值模拟,发现了颗粒系统的统计量存在尺度依赖性,并提出了新的阻力关联式修正。以上均反映了采用IMB 处理运动固体边界具备巨大潜力。
然而,IMB 中的权重系数作为实现流固耦合的重要参量,其形式依据经验确定[6]。文献表明其在颗粒雷诺数小于5 的情况下可以保证精度[18],但存在粘度依赖问题[19]。Wang 等[20]提出了一个广义权重函数,其增大了各固含率下对固体权重的预测,结合双松弛时间(two-relaxation-time,TRT)模型[21]用以修正粘度依赖;但在中等雷诺数下其和原始的权重函数一样,存在固体受力预测值偏高的问题。
本文在原始权重函数的基础上,提出了一个改进的权重函数,通过引入零固含率处的权重因子多阶导数为0 作为限制条件,改善中等雷诺数下固体受力的预测精度。通过静止圆柱绕流、Taylor-Couette 流和振动圆柱绕流验证该函数的有效性,表明改进的权重函数可作为一种合理的浸入运动边界方案。
1 数值方法
1.1 格子Boltzmann 方法
标准的格子Boltzmann 方法将密度分解为多个方向离散的分布函数,并在格点网格内将各分布函数碰撞迁移,通过对当前格点上各分布函数的组合还原出密度、速度等宏观量。其方程形式为:
其中,fi(x,t)为t时刻位于x格点的第i个分布函数;ci为格子速度,二维下一般采用9 个方向的分布函数,三维下一般使用19 或27 个方向的分布函数,如图1 所示;∆t为时间步长;ci∆t为空间步长;Ω(f)为碰撞算子。单松弛下,方程(1)为:
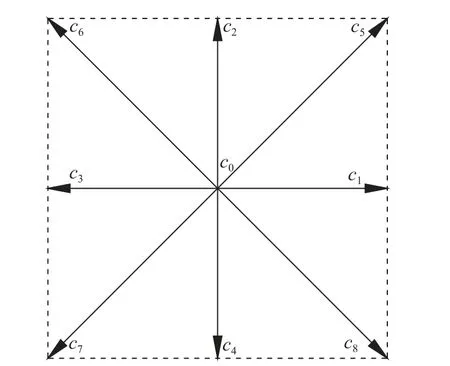
图1 D2Q9 模型Fig.1 D2Q9 model
通过对分布函数求零阶矩和一阶矩即可更新当前格点下的流体速度u和流体密度ρ:
1.2 流固耦合实现
Nobel 等[6]提出的IMB 方法如图2 所示,其通过引入格子控制体和格子固含率 εs统一描述流体、固体和流固边界。
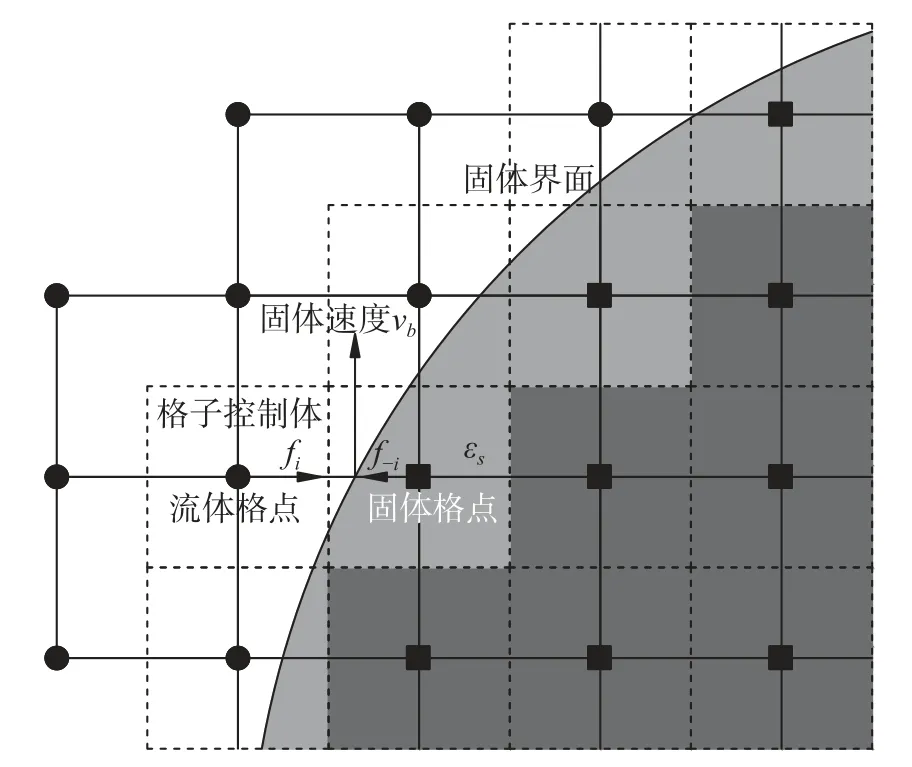
图2 IMB 方法示意图Fig.2 Schematic diagram of the IMB method
εs表示固体部分在格子控制体中的体积分率,εs=0 表示格点内全部为流体,εs=1 表示格点内全部为固体,固体边界的固含率介于0 和1 之间,这样便可实现对边界的平滑描述。
进一步地,基于非平衡态反弹的思想,在标准单松弛的LBM 中引入额外碰撞项描述固体作用:
式中,us为覆盖在格点上的固体速度,u为格点的流体速度,−i代表与i反向;β(εs,τ)为权重函数,控制流体碰撞算子和额外碰撞项的计算比重,同样满足β ∈[0,1]。β为1 时完全由固体的额外碰撞项控制;β为0 时完全由流体控制,方程还原为标准的单松弛LBM 方程。β的形式较为固定,一种可直接令 β=εs,另一种应用更广泛的形式为[6]:
固体颗粒所受的力F和力矩T通过求和所有颗粒覆盖固体格点的动量变化得出,分别为:
其中xj和xc分别为被颗粒覆盖的固体格点位置和颗粒中心格子位置。
1.3 改进的流固耦合权重函数
由上节可知,β在流固耦合中起到重要作用,而目前其形式通过经验确定。在实际应用中发现原始的 β(εs,τ)在雷诺数提高后计算的固体受力值偏高,很有可能其对固体组分的权重做了过高预测,可对其做进一步改进,构造时至少满足以下原则:
在此基础上,基于Noble 的形式引入以下假设:
即在固含率为0 处使 β关于固含率的b−1 阶导均为0,相应的改进形式如下:
b=1 时方程(16)还原为原始的方程(10)形式。图3 为 τ=0.6时不同b下权重函数随固含率的变化。b>1 时,方程在固含率为0 附近的过渡更加光滑,且整体上减小了原 β的预测值,b越高则修正效果越强。
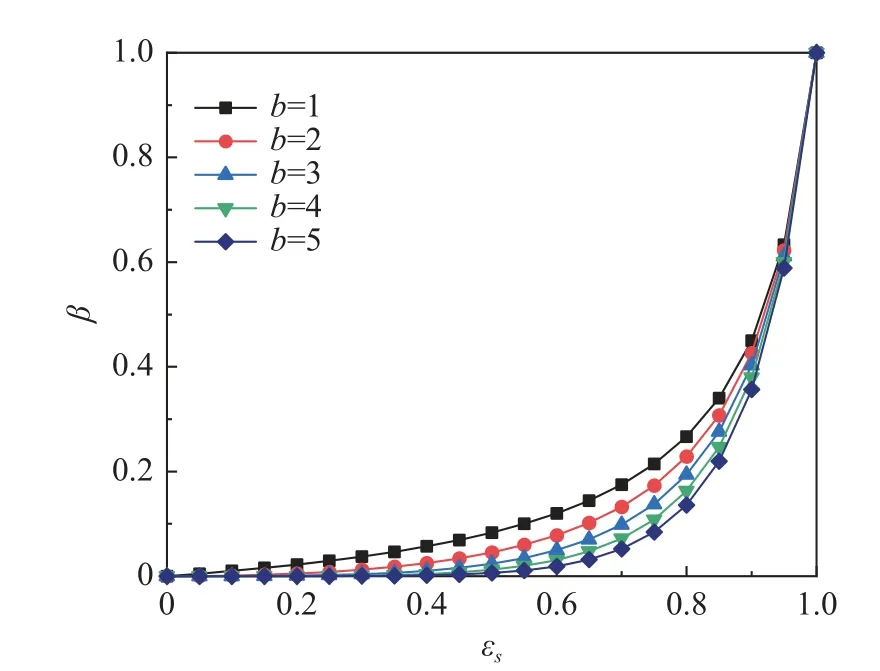
图3 τ=0.6时不同b 下β 随固含率的变化Fig.3 Variation of β with εs for different b at τ =0.6
2 数值验证
2.1 静止圆柱绕流
为了验证权重函数的修正效果,本文采用上述方法,基于不同b的权重函数验证不同雷诺数下均匀来流静止圆柱绕流问题,并与文献[23-26] 的结果对比。求解区域如图4 所示。
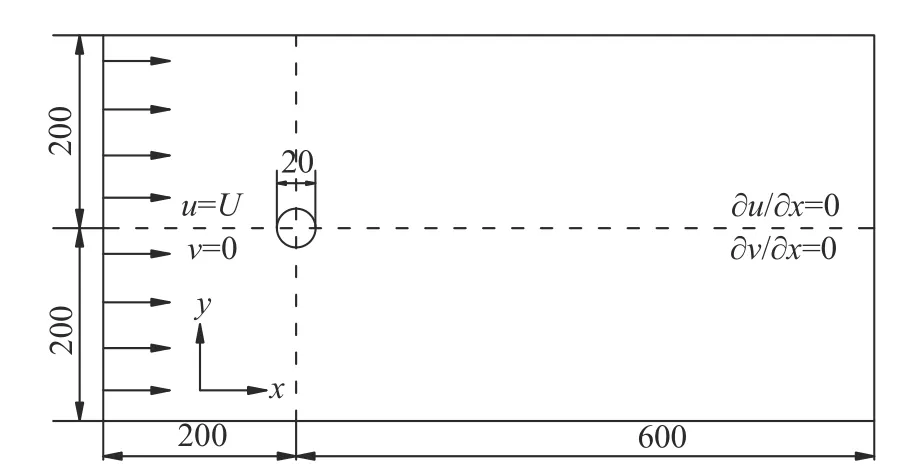
图4 圆柱绕流计算域及边界条件Fig.4 Computational domain and boundary conditions for flow around a cylinder
计算区域为矩形,长和宽分别为800 和400,流体运动黏度 υ=1.881×10−2,密度 ρ=1,圆柱直径D=20。计算域左侧为均匀来流入口边界,速度u=U、v=0,采用Zou &He 边界[22];上下两侧均为周期边界;右侧为自由出流边界,采用Neumann 边界,即∂u/∂x=0、∂v/∂x=0。获得圆柱的受力后,可通过下式分别计算阻力系数和升力系数:
式中Fx和Fy分别为流体对圆柱作用力在x和y方向的分量。
通过调整来流速度U实现不同雷诺数的计算,结果如表1 所示。各雷诺数下原始权重函数(b=1)所计算的阻力系数和升力系数均高于文献[23-26]的结果,且雷诺数越大,偏离参考值越大,即公式(10)过高估计了固体的受力。随着b的增加,不同雷诺数下所计算的升力系数和阻力系数均开始减小,b=3、Re=100、200 时阻力系数开始与文献值接近。图5为b=3、Re=100、200 时,达到动态稳定后圆柱的阻力系数和升力系数随时间的演化曲线,结果均呈现明显的周期性。随着b进一步增大,各雷诺数下阻力和升力系数将进一步降低。以上说明在较小雷诺数下公式(10)具备一定的预测性能,随着雷诺数提高,公式(10)低估了流固边界中流体组分的作用,需要相应地降低固体权重,提升固体边界的渗透性以增强流体的作用强度。
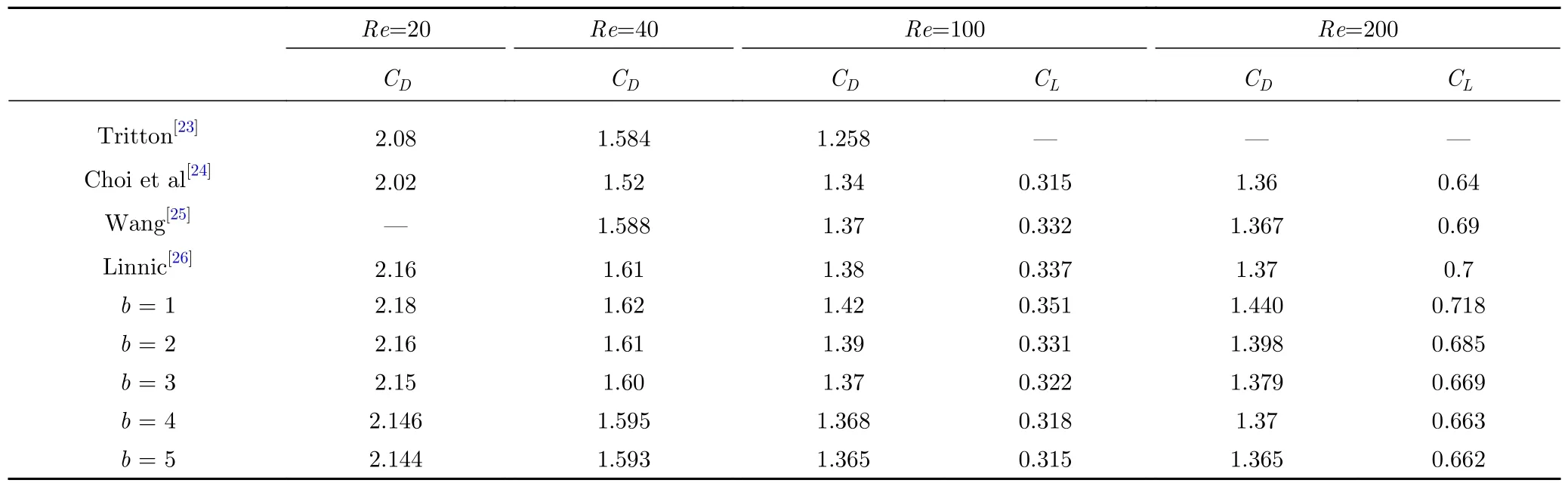
表1 不同雷诺数下圆柱的阻力系数和升力系数Table 1 Drag and lift coefficients of the cylinder at different Reynolds numbers
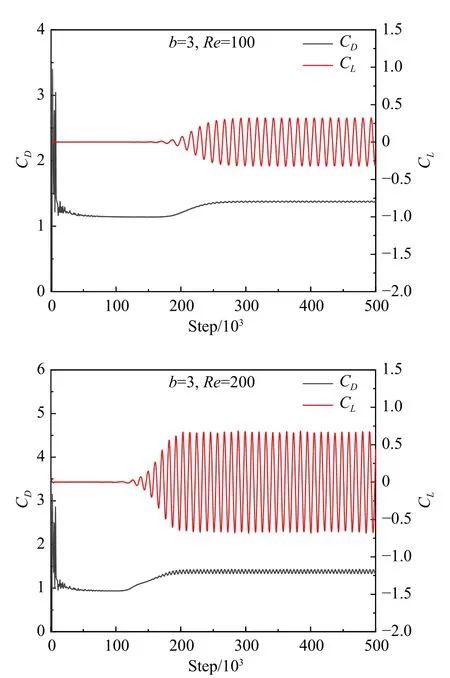
图5 b=3 时,Re=100、200 对应阻力系数和升力系数随时间的演化Fig.5 Time evolution of the drag and lift coefficients at Re=100,200 for b=3
图6 为b=3 时不同固含率下公式(16)随黏度的变化曲线,并与公式(10)对比。改进权重函数的β值均小于原始权重函数解,固含率越高修正效果越弱;固含率较低时黏度越大,改进的权重函数修正效果越强。结合表1 分析表明,中等雷诺数下增加固体边界的渗透性有利于获得更加准确的结果。
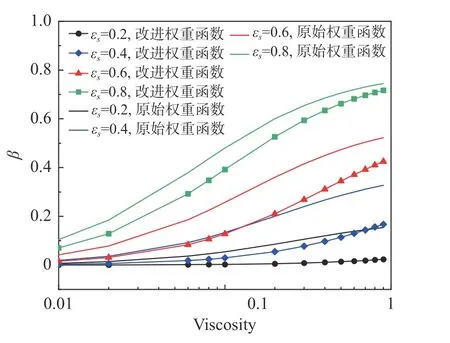
图6 权重函数随黏度的变化对比Fig.6 Comparison of the improved weighting function and the original weighting functionfor varying viscosity
2.2 Taylor-Couette 流
二维Taylor-Couette 流是流体力学中少数存在解析解的流动(仅限层流时),如图7 所示。当内筒以角速度 ω1旋转,外筒以角速度 ω2旋转时,内外筒间的速度分布为:
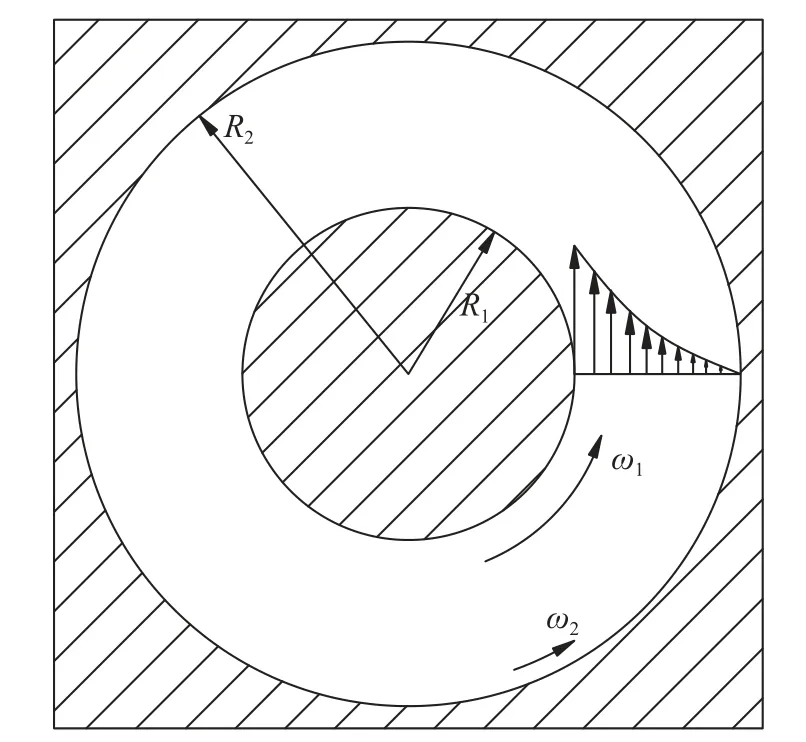
图7 Taylor-Couette 流示意图Fig.7 Schematic diagram of the Taylor-Couette flow
式中,R2为外筒半径,γ为内外径之比:γ=R1/R2,r为该点与圆心的距离。该算例为曲线运动边界主导的流动,可用于检验运动边界的性能。
采用320 × 320 的矩形网格,在中心点放置同心圆筒,基于b=3 的改进浸入运动边界对流场进行验证。流体运动黏度 υ=0.2,密度 ρ=1。外筒半径R2=150,ω2=0,内筒边界线速度为0.007 5。同时,定义L2 范数误差:
式中uLB为采用该方法数值求解的流体格点速度。
图8 为b=3 时,改进浸入运动边界计算的流场与精确解对比,不同 γ下中心区域的流场均与精确解吻合较好。γ=0.8 时内外筒边界附近与精确解存在偏差,可能是该情况下解析流体的格点数量较少,边界对周边流场产生了扰动。
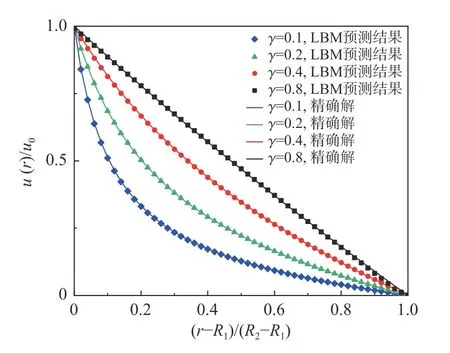
图8 b=3 时,基于改进权重函数得出的不同 γ下预测速度与精确解对比Fig.8 Comparison of the predicted velocities based on the improved weighting function (b=3) and the exact solutions for differentγ
表2 为不同 γ下b=1 和b=3 时,L2 范数的误差对比。b=3 的改进权重函数和b=1 的原始权重函数均不同程度地减小了误差,γ=0.1 和0.2 时的效果最为明显,误差分别降低了61.5% 和76.7%,整体平均误差降低了38.5%。以上表明改进的浸入运动边界相较于传统边界可以提升流场的准确性。
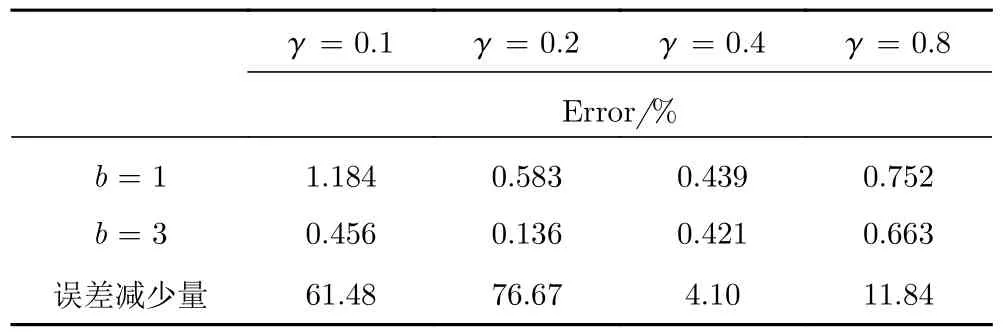
表2 不同γ 下改进权重函数(b=3)与原始权重函数(b=1)计算Taylor-Couette 流与精确解误差对比Table 2 Error comparison of the Taylor-Couette flow computed with the improved (b=3) and the original (b=1)weighting functions
进一步地,基于 γ=0.5 的情况,令外径物理长度为2.0,采用x=2.0/32、2.0/64、2.0/96、2.0/128、2.0/160的网格分辨率,以内径作为特征长度,对Re=10 的情况进行精度验证。由图9 可知,算法整体保持了一阶精度,b=1时的精度为1.041,b=3时的精度为1.039,b=5 时的精度为1.032。算法接近一阶精度的原因是该算例基于固体边界驱动流场,当固含率εs=1.0 时,方程(8)和方程(9)恢复成具有一阶精度的标准反弹格式。固体内部格点虽不纳入误差计算,但依然基于方程(8)执行碰撞迁移步骤会对流体区域产生一定影响。同时b=3 的误差曲线低于b=1 和b=5的结果,表明改进的浸入运动边界在改善流场准确性的同时,不会降低边界的收敛阶。当b继续提高时,对比b=3 和b=5 的误差线,可发现其误差会有所提高,因此可将b=3 作为一个较优的参数。
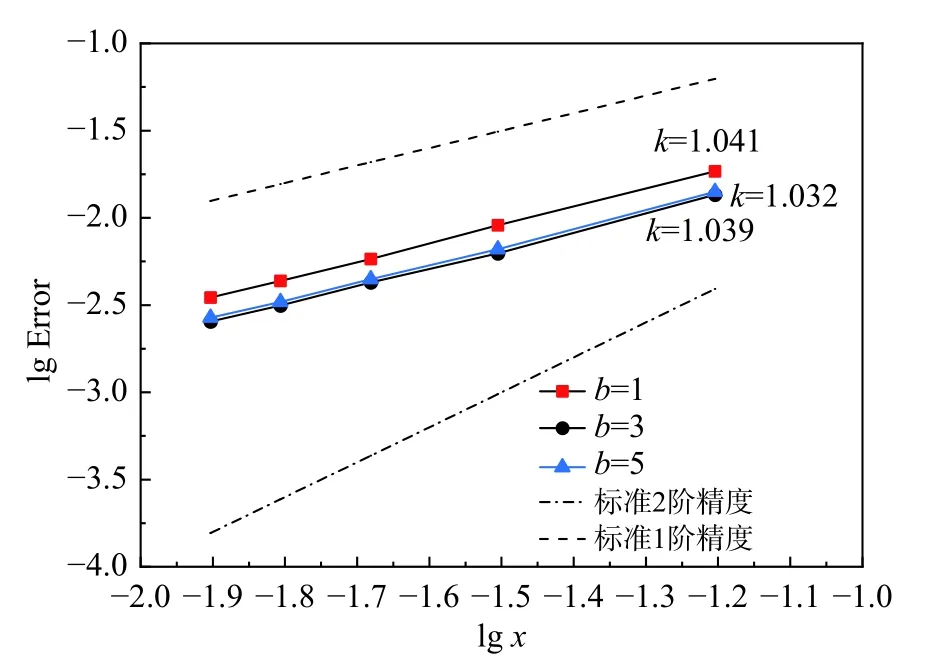
图9 改进浸入运动边界的收敛阶Fig.9 Convergence order of the improved immersed moving boundary
2.3 振动圆柱绕流
本节基于b=3 时的权重函数,分析均匀来流下圆柱沿y方向周期性正弦振动的动力学现象。当圆柱振动频率与圆柱的自然涡脱落频率相近时,圆柱升力系数波动频率将与振动频率一致,称为“锁频”现象,其结果受模拟方法影响较为明显。为了验证圆柱振动的锁频区间,选用频率比k=fe/f0作为无量纲参数,其中fe和f0分别为圆柱振动频率和自然涡脱落频率,由2.1 节Re=100 算例测得f0=7.9 × 10−5,模拟的计算域和边界与图4 一致。Koopmann[27]通过实验得到圆柱锁频区间为k=0.75~1.25,且在k=1.0 两侧对称分布。本文对Re=100、圆柱沿y方向振幅比为A/D=0.25 的情况进行模拟,记录k=0.5、0.9、1.0、1.1、1.5 下圆柱的升、阻力系数以及升力系数能量谱,并与文献[27-29]结果对比。
图10 展示了动态稳定后圆柱运动到最下端的涡量场,图10(b、c)中的尾涡分布较为均匀和规则。由图10(a、d)可以看出:当圆柱振动频率偏离自然涡脱落频率较远时,圆柱后方尾涡将不再对称,振动频率越高,脱落的涡尺寸越大。
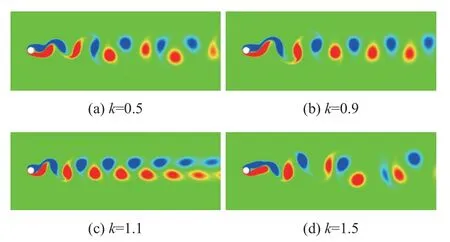
图10 圆柱振动到最下端时尾部涡量图(Re=100、A/D=0.25)Fig.10 Vorticity distributions as the cylinder oscillates to the bottom at Re=100,A/D=0.25
图11 为稳定后,不同振动频率下圆柱升力和阻力系数的随时间演化曲线及升力系数的能量谱结果。由图11(a)可知,当k=0.5 时,CL曲线中高幅值波和低幅值波交替出现,即拍频现象,能量谱呈现双峰形态,此时升力同时由fe和f0控制,主控频率为f0,圆柱处于锁频区间之外;k=0.9 和k=1.1 时,升力系数随时间的演化曲线不再由f0控制,而是锁定在fe附近,此时处于锁频区间内。由图11(d)可知,k=1.5 时,升力系数曲线再次出现拍频现象,主控频率为fe,处于锁频区间外。
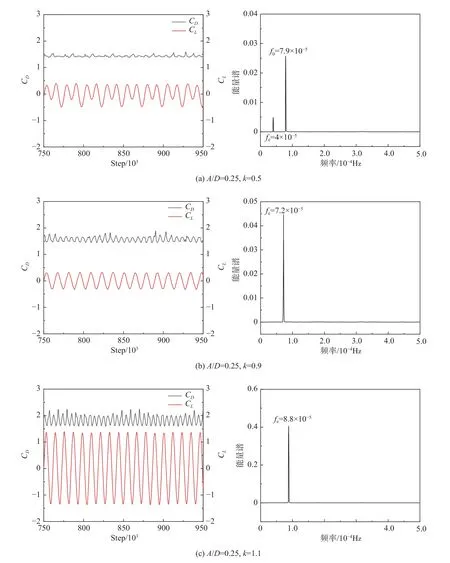
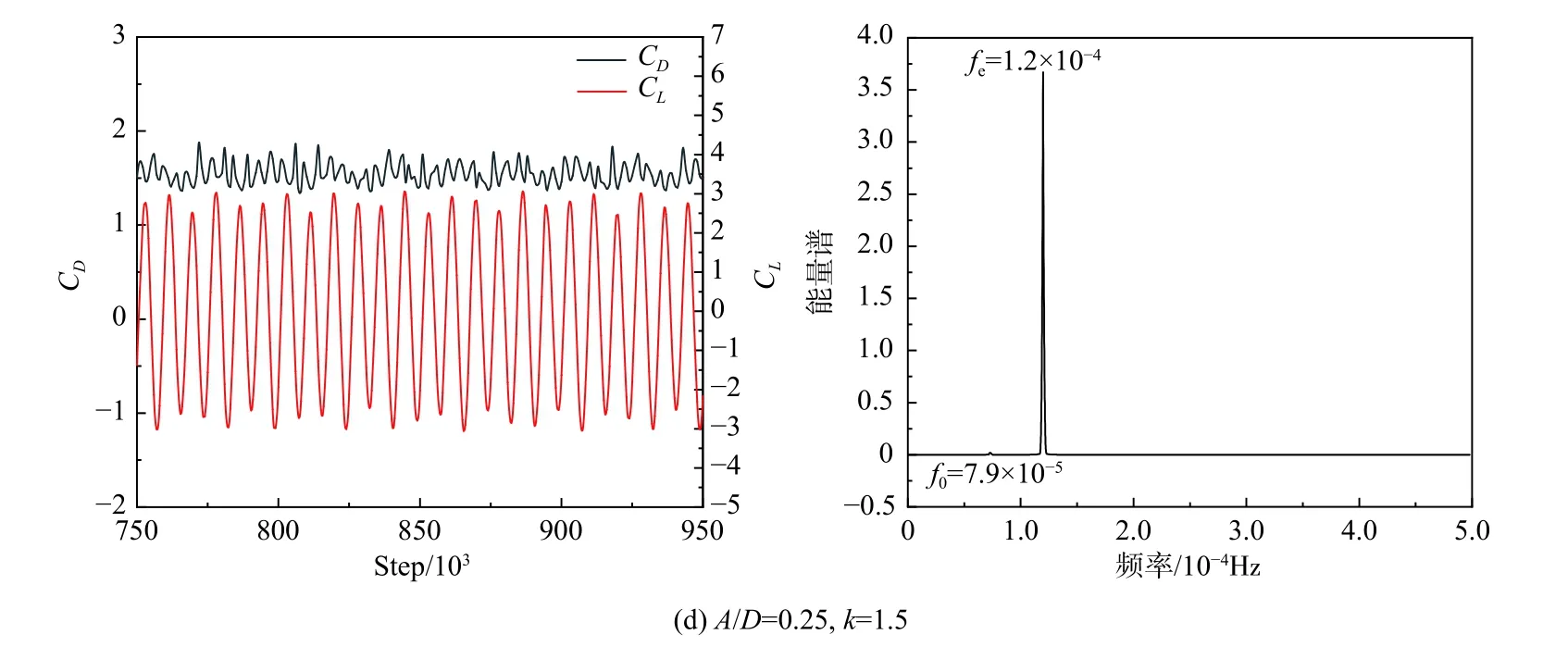
图11 A/D=0.25 时,不同振动频率下圆柱阻力系数和升力系数随时间的演化及升力系数的能量谱Fig.11 Time evolution of the drag and lift coefficients under different oscillation frequencies,and the power spectra density of the lift coefficient at A/D=0.25
图12 为Re=100、A/D=0.25 时,阻力系数均值CDmean随频率比k的变化规律,所得结果与Placzek等[29]的计算结果一致:CDmean随着k的增加先增大后减小,在锁频区间内k=1.1 时取得极大值。由图12可知,采用b=3 的改进权重函数计算的CDmean明显与Placzek 等[29]的结果更为接近,表明本文提出的权重函数在中等雷诺数下可以对固体的动力学信息做出修正,可将该改进边界算法应用于处理复杂的流固耦合问题。
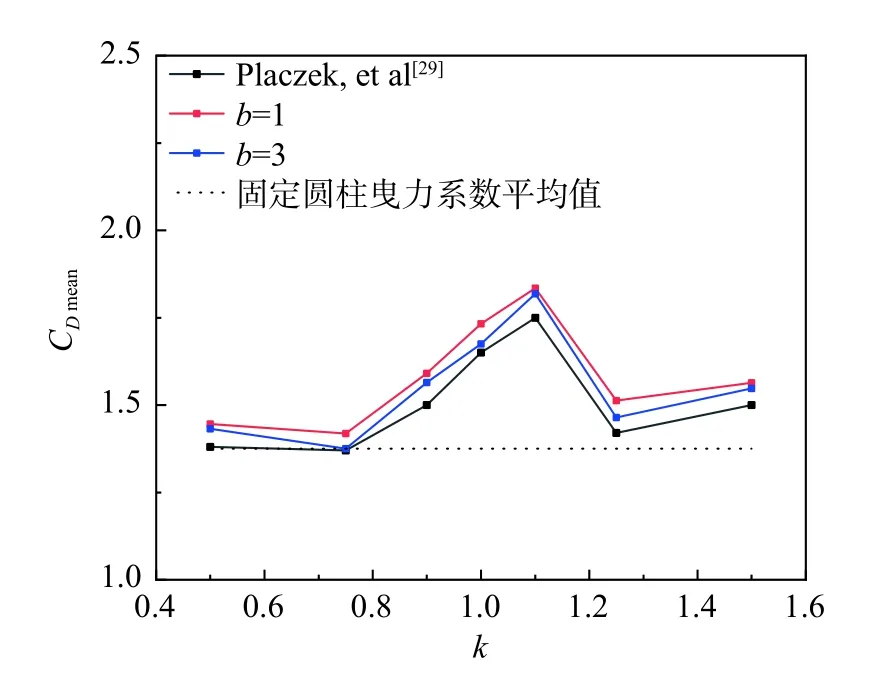
图12 阻力系数均值CDmean 随频率比k 的变化规律(Re=100、A/D=0.25)Fig.12 Variation of the averaged drag coefficient CDmean with the frequency ratio k at Re=100,A/D=0.25
3 结论
本文提出了一种LBM 框架下的改进浸入运动边界,通过假定零固含率处的权重因子多阶导数为0 来减小固体权重的过高预测,且当可调参数b=1 时权重函数还原为原始形式。由静止圆柱绕流和Taylor-Couette 流测试,通过一定程度地降低固体组分的权重,不仅获得更为合理的固体动力学参数,还提升了流场预测的准确性,b=3 时的改进效果最佳。将修正后的权重函数应用于振动圆柱绕流问题,成功复现了圆柱振动时的锁频现象,且得到的阻力系数更准确,表明该函数下的浸入运动边界具备普适性,对后续流固耦合问题预测的改进具有较高价值。后续将开展修正参数的模化工作,探索边界处局部速度与修正参数的关联,实现权重函数的自动调整以拓宽IMB的应用场景。
