可渗透面对流FW-H 方程伪声产生机制和抑制方法
2023-08-03何嘉华王垿桁刘秋洪钱振昊
何嘉华,王垿桁,刘秋洪,钱振昊
(西北工业大学 翼型、叶栅空气动力学重点实验室,西安 710072)
0 引言
声比拟方法是工程中应用最广泛的气动噪声数值预测方法[1-2],先对有限区域内流动进行高保真数值计算以精确模拟噪声的产生,然后假设声波从近场到远场线性运动,通过求解基于Lighthill 声比拟思想的标准波动方程或标准对流波动方程,比如FW-H 方程[3]和对流FW-H 方程[4,5],来快速预测噪声的传播。在实际应用中,FW-H 方程和对流FW-H 方程多采用非物理的封闭可渗透面作为积分面,完整解由面积分和体积分组成。如果可渗透面足够大,声波的产生、反射和折射等过程都包围其中,即可忽略体积分对声场的贡献[6],从而积分面外的声场仅利用可渗透面上的厚度源和载荷源信息计算,比如解析公式F1A[7]和F1C[4]。
对绕流和射流等实际噪声问题,为了保证可渗透面上气动声源具有足够精度,选择的可渗透面往往穿过一定非线性区域。近场流动的非线性扰动同时包含了声波和涡波,涡波衰减缓慢且沿平均流向下游传播,当通过可渗透面时,涡波扰动不可避免地被收集为积分面的输入而产生伪声[8]。学术界对伪声产生机制的理解存在可渗透面急剧截断积分区域导致谱泄漏和声比拟方程求解方法破坏源项滤波功能的分歧[9-12]。Morfey 等[9]研究发现,考虑可渗透面外体积源项的贡献即可消除伪声污染。Rahier 等[10]通过理论分析和数值试验明确指出,伪声污染就是忽略四极子体积源项贡献引起的。Obrist 等[11]的研究显示,可渗透面急剧截断积分区域会导致面积分源项频谱泄漏,从而产生污染声场的伪声。Mao 等[12]细致分析了对流FW-H 方程的右端面源,提出了与Obrist 等不同的观点,认为载荷源和厚度源能自动过滤自身包含的涡波伪源,但数学演绎过程即便对静止可渗透面也不严格成立。
远场噪声的准确预测需要采用有效方法抑制伪声干扰。最简单的方法是直接舍弃可渗透面中部分允许涡波通过的片区[13-14],通过对非封闭可渗透面积分来预测噪声。然而FW-H 方程的推导建立在封闭可渗透面基础上,因此使用非封闭积分面的方法在数学上是不正确的。Spalart 等[15]采用多个相邻可渗透面来提取声源,最终声场是这些可渗透面积分结果的平均值。Mendez 等[16]给出了估计可渗透面数量和位置的表达式。Obrist 等[11]建议使用平滑变化的空间窗函数来减少截断误差。Wright 等[17]提出了一个广义FW-H 方程,利用不同权重的可渗透面数据或有限厚度的体积源来降低伪声强度。利用多可渗透面数据或有限厚度体积源贡献抑制伪声方法会导致声源存储量和声学计算量的增加。Ikeda 等[18]将无穷薄厚度体积源贡献转化为面积分,提出了适用于声学远场的附加面源伪声抑制方法。Zhong 等[8]从线化Euler方程出发,发展了一种考虑可渗透面局部非均匀流影响的声远场外推方法,其核心思想是利用扰动速度的散度 ∇·u′和物质导数 D∞u′/Dτ自动过滤涡波,但增加了积分面源项的计算困难。Mao 等[12]建议采用Kirchhoff 积分方程预测噪声传播以抑制伪声污染,但Kirchhoff 积分面仅适用于线性区域。
明晰涡波伪声产生机制可为伪声干扰抑制方法的发展指明方向。本文以运动介质中的声传播为例,通过耦合分析对流FW-H 方程的载荷源和厚度源,阐明涡波伪声的产生机制。在此基础上提出一种伪声干扰抑制方法,并利用算例验证其正确性。
1 可渗透面涡波伪声产生机制
假设无穷远均匀来流的密度、压力和速度分别为ρ∞、p∞和u∞i(对应马赫数为Ma∞i),将当地流动分解为均匀来流和非稳态扰动两部分:
引入运动速度为vi(对应运动马赫数为Mai)的可渗透面f=0,可渗透面内部和外部区域分别定义为f<0和f>0,且可渗透面单位外法线矢量满足n=∇f。对流FW-H 方程可表示为[4-5]:
方程左端c∞和H(·)分别表示均匀运动介质中的声速和Heaviside 函数;方程右端 δ(·)表示Dirac delta 函数;物质导数 D∞/Dt定义为:
右端3 项分别代表四极子体积源、偶极子载荷源和单极子厚度源,张量Tij、Li和Q定义为:
式中,δij为 Kronecker delta 函数,σij为黏性应力张量,下标i,j=1,2,3表示直角坐标方向(对二维问题i,j=1,2)。
1.1 对流FW-H 方程源项的涡波自动过滤功能
可渗透面的选择应遵循一定规则,即在瞬态流动参数精确解析前提下,可渗透面应覆盖声波的产生、反射和折射等主要过程,并使得可渗透面处的平均流近似均匀。如果涡在流动中快速发展或衰减,或彼此之间有强相互作用,就会产生不可忽视的声辐射,可渗透面应包围这些区域。也就是在一个恰当的可渗透面处,涡波衰减缓慢,且不会产生明显的压力和密度扰动。由于主要的气动声源位于可渗透面内,忽略体积源贡献不会引起明显的数值误差,因此公式F1A[7]和F1C[4]仅根据积分面上的厚度源和载荷源评估可渗透面外声场,以提高计算效率。
对高雷诺数流动,黏性应力张量因对远场的贡献小而被忽略,从而载荷源源参数Li可近似为:
非加热流体的运动速度可以分解为无旋分量和有旋分量两部分,其中扰动速度的无旋分量和有旋分量分别对应于声波和涡波分量[19],也就是:
其中下标a和v分别表示声波和涡波分量。利用式(1)和式(8)可将式(6)等价表述为:
其中,右端前两项分别代表一阶的声波扰动和涡波扰动,后两项分别表示二阶的声-声干扰和涡-涡干扰。同理,式(7)可等价写为:
其中,右端前两项分别代表一阶的声波扰动和涡波扰动,紧接着的3 项分别表示二阶的声-声干扰、涡-涡干扰和涡-声干扰,最后两项分别为三阶的声-声干扰和涡-涡干扰。
理论上讲,式(9)和式(10)中非线性的涡-涡干扰和涡-声干扰能够诱导声辐射,应该视为声源的一部分。但在通常情况下,可渗透面处的声波和涡波扰动速度远小于平均流速度,因而可渗透积分面上的厚度源和载荷源强度主要取决于一阶扰动项。已有的研究表明,均匀流中的一阶涡波扰动项仅表征对流效应[20],不能产生声波扰动,即不会诱发声辐射,属于伪声源。定义:
当可渗透面外法线方向与均匀平均流方向并非完全一致时,D∞[∇H(f)]/Dt非零,因此方程(16)并不严格成立。
方程(14)减去方程(15)即可得到对流FW-H 方程(2)右端的伪声源之和为:
方程(17)并没有限定可渗透面静止,可见对流FWH 方程(2)的面源项确实能够自动过滤涡波伪声源。
忽略黏性和非等熵效应,应力张量Tij可展开为:
由于非线性涡-涡干扰和涡-声干扰属于声源,且应力张量Tij不存在一阶涡波扰动,故体积源项不含有伪声源。忽略体积源对声场的贡献会导致一定数值误差,但不会产生伪声辐射[20]。因此,可渗透面急剧截断空间积分区域不是伪声产生的根源。
1.2 对流FW-H 方程求解过程的伪声引入
对流FW-H 方程的求解可以采用对流格林函数,以便将均匀流对流作用包含在格林函数中。假设均匀流亚声速运动,三维时域格林函数可表示为[4-5]:
其中,g代表延迟时间函数,x和t表示观察点的位置与时间,y和 τ表示声源的位置与时间,声学半径 ℜ和R定义为:
式中,R 表示欧式空间,G为对流格林函数。根据方程(17)可知,对源项直接求物质导数和散度可自动过滤涡波,因此依据方程(22)积分得到的结果能够消除涡波干扰,但需要数值计算右端项的空间导数,其过程复杂且易导致不必要的数值误差[21]。令Qa=Q−Qv和La=L−Lv,利用分部积分得到:
根据Farassat 提出的积分方法[7],方程(23)右端前两项的积分结果均为零,因而被忽略。利用格林函数性质D∞G/Dτ=−D∞G/Dt与∂G/∂yi=−∂G/∂xi,并将声场分解为厚度噪声和载荷噪声两部分,有:
其中下标T和L则分别表示厚度噪声和载荷噪声分量。方程(24)和方程(25)中,利用了函数 δ(f)的性质将体积分降阶为f=0处的面积分。厚度噪声和载荷噪声积分公式的详细推导过程见参考文献[4-5]。
由于Qa和La与一阶涡波扰动无关,方程(24)和方程(25)的积分结果不含涡波伪声。然而,对数值模拟得到的扰动速度场u′,一般难以实现涡波速度分量的分离,因此声压积分公式(比如公式F1C[4])直接采用变量Q和L计算厚度噪声和载荷噪声:
当有涡波通过可渗透面时,涡波扰动不可避免地被收集为积分面的输入,从而导致伪声辐射。伪声的厚度分量和载荷分量可表示为:
大量的研究结果[4-5]显示,方程(26)和方程(27)对声学问题是成立的,即忽略方程(23)右端前两项积分贡献是正确的。可渗透面处存在涡波扰动时,如果声传播仍然采用方程(26)和方程(27)计算,则下述积分项贡献也被忽略了:
根据方程(17),可渗透面处的涡波伪声源是可以自动过滤的,那么有:
也就是说,被方程(26)和方程(27)忽略的积分项贡献可以抵消涡波伪声。
通过上述分析可以知道,尽管载荷源和厚度源能够自动过滤涡波,但按照Farassat 方法,波动方程求解采用了分部积分,最终的声传播积分方程忽略了部分积分项的贡献,因难以实现涡波速度分量的分离,使得积分结果引入了涡波伪声辐射。
2 可渗透面伪声抑制方法
Farassat 积分方法对仅含声波分量的源项积分有效,而对含有涡波分量的源项积分失效。将可渗透面源项拆分为仅含声波分量项和可含涡波分量项两部分。对流FW-H 方程(2)可等价变形为:
2.1 时域积分公式
可渗透面外声场的积分解可表示为:
将三维对流格林函数式(19)代入上述两个方程,得到厚度噪声和载荷噪声的半解析积分公式为:
对可渗透面固定不动的特殊问题,如CAA/CFD计算或风洞声学问题,参数 ℜ与R、可渗透面外法向矢量n和声源运动速度v(等于零)不依赖于延迟时间,且延迟时间可采用显式方法获取。方程(38)和方程(39)可进一步写为:
2.2 频域积分公式
若可渗透面周期性运动,如匀速平移、恒速旋转和静止不动,噪声预测可在频域下实施。对时域信号ξ(t)和频域信号(ω),若Fourier 变换对为:
其中,ω为角频率,j为虚数单位。那么三维频域对流格林函数为:
其中k=ω/c∞为声学波数。对方程(38)和方程(39)两端进行Fourier 变换,得到声压频域积分解为:
当可渗透面静止时,可进一步简化为:
将频域声压信号执行Fourier 逆变换,即可得到声压的时间历程。如果声学问题是二维的,则采用二维频域对流格林函数[22]进行积分,此处不再详述。
上述涡波伪声抑制方法的核心思想与文献[8]是一致的,即利用了扰动速度的散度 ∇·u′和物质导数D∞u′/Dτ能自动过滤涡波的特性。需要进一步指出的是,前文分析过程默认可渗透面处涡波不会产生压力和密度扰动。恰如文献[8]所强调的,若湍流中存在对流的涡波压力或密度扰动,当其通过可渗透积分面时,预计仍会存在伪声辐射。更具体地说,因参数Q′和L′中的压力和密度扰动含有非声学的成分,必将对伪声的产生做出贡献,此时应重新选择可渗透面,尽量避免或弱化非声学的压力或密度扰动。
3 均匀流算例数值验证
利用具有理论解的流动算例验证涡波伪声的产生机制和抑制方法。假设密度 ρ∞=1.216 kg/m3的均匀流沿x1轴正向运动,马赫数Ma∞=0.5。首先考虑自激角频率 ω=680 rad/s的单极子声辐射,证明算法对纯声学问题的有效性;然后利用均匀流中的对流涡算例检验算法的涡波抑制效果;最后将单极子与对流涡叠加在一起,数值验证涡波伪声的产生机制。所有算例中,取声速c∞=340 m/s。
3.1 均匀流中的单极子
均匀流中静止单极子的三维声场可以用一个简单的谐波速度势函数来描述:
其中,A为速度势函数的幅值,参数 ℜ和R分别由式(20)和式(21)定义。点源诱导的声学速度、压力和密度场为:
单极子位于坐标原点,选择边长a=4.0 m的正方体表面作为可渗透面包围点源(如图1 所示),采用均匀的结构化网格离散可渗透面,网格总数38 400。可渗透面处瞬态流动参数(包括压力、密度和速度)由流场精确解产生。对线性声学问题,忽略源项中的非线性作用。36 个观察点均匀布置在x3=0平面内一个半径为r=34 m的圆上,将基于x1轴测量到的观察点与坐标原点间的几何角度定义为观察角 θ。取A=0.1 m2/s,单极子诱导的瞬时声学压力和声学速度场在x3=0平面内的空间分布分别如图2 和图3 所示。因平均流对流作用,点源上游的声波被压缩,而下游的声波则被拉伸。
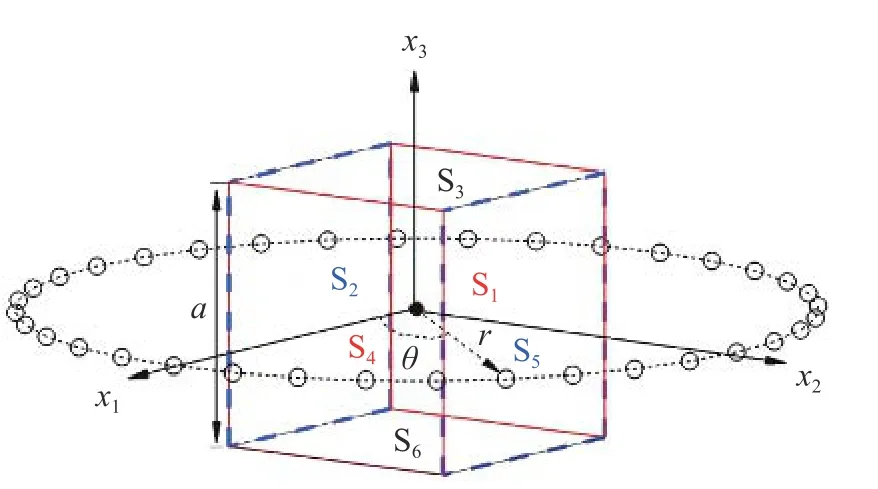
图1 单极子、可渗透面和观察点示意图Fig.1 Schematic of monopole,permeable surface,and observers
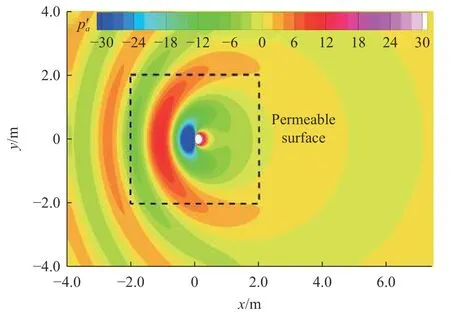
图2 静止单极子诱导的声学压力场Fig.2 Pressure field induced by a stationary monopole
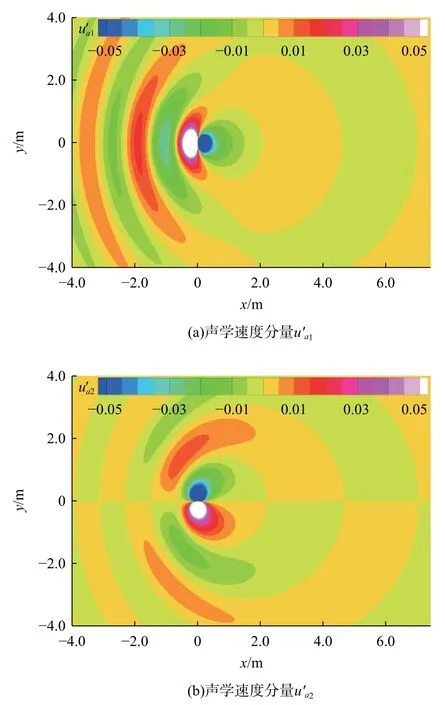
图3 静止单极子诱导的声学速度场Fig.3 Velocity field induced by a stationary monopole
时域声压预测公式中的时间导数和空间导数采用二阶有限差分方法近似,在每个声源周期T内布置128 个时间步,空间步长则取为5 mm(与可渗透面的网格间距不一致),以保证差分算法的数值精度。观察点声学信号采用超前时间算法[23]计算。将含有伪声抑制算法的声场数值预测结果称为CFW-H 解。图4(a)和图4(b)分别为点源下游 θ=30◦和上游θ=150◦处的声压时间历程预测结果,CFW-H 数值解与理论解、FW-H 积分方程解都吻合。对仅含声模态的噪声问题,应尽量采用经典方法去外推声传播,比如对流FW-H 积分方程,以避免空间导数的计算。
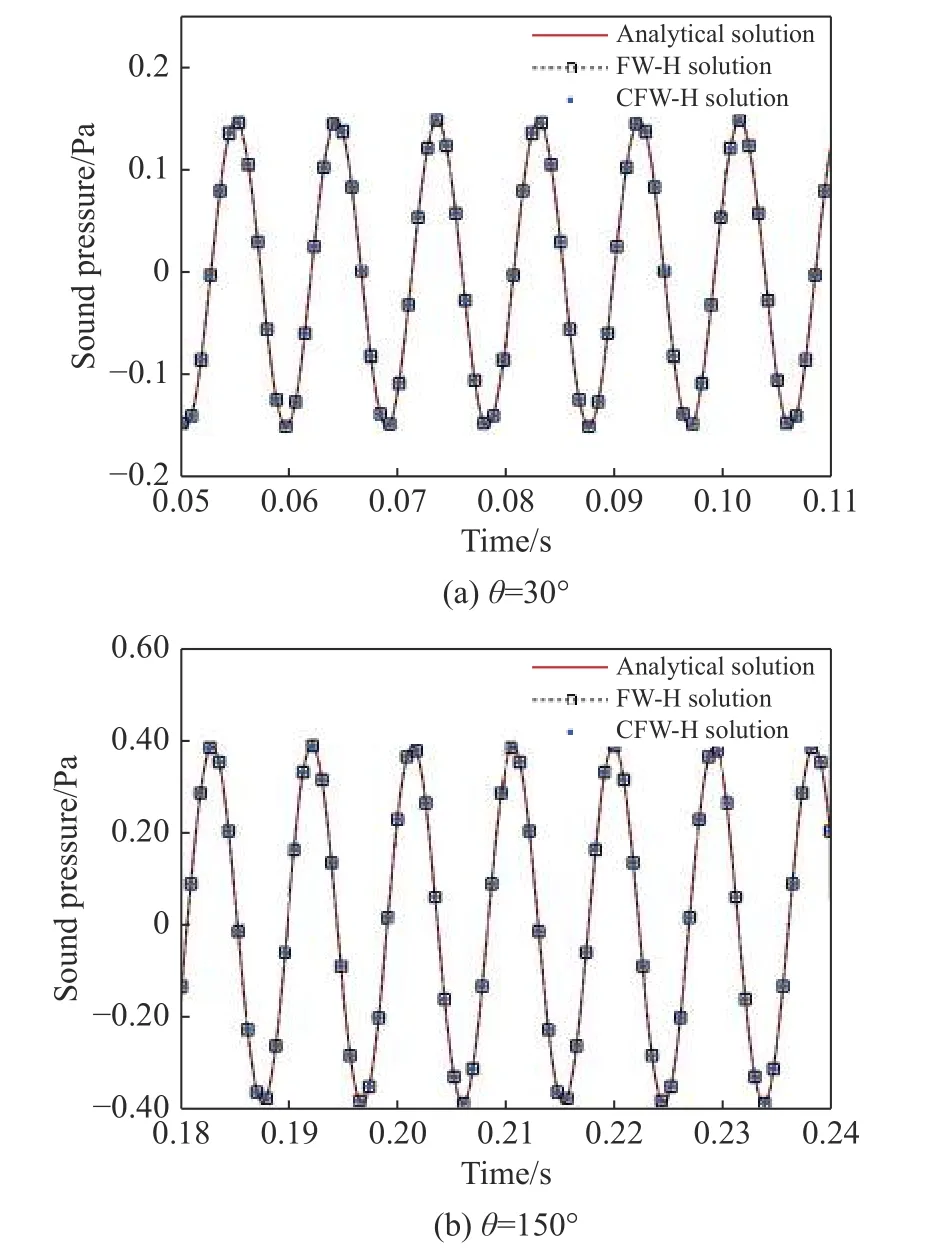
图4 静止单极子声学压力时间历程Fig.4 Pressure time histories induced by a stationary monopole
3.2 均匀流中的对流涡
均匀流中的对流涡算例常用于检验涡波伪声抑制方法。对流涡随平均流运动,假设在t=0时刻通过(0,0)点,其诱导的速度场为:
仍采用图1 所示的正方体6 个表面(S1~ S6)作为可渗透面。实际物理问题中,涡波随平均流向下游运动,仅在 S4面上存在涡波干扰。因此本算例忽略S4之外的5 个面上的涡波速度场,而且不考虑对流涡诱导的压力和密度扰动。对小振幅涡波扰动,不计入伪声源非线性项的贡献,分别采用FW-H 积分方程和伪声抑制方法预测远场噪声。在点源下游 θ=30◦和上游 θ=150◦处,对流涡诱导的伪声时间历程数值预测结果分别如图6(a)和图6(b)所示。均匀流中的对流涡不会诱发能辐射到远场的声波。FW-H 数值解在对流涡通过 S4面前后会产生伪声辐射,噪声预测结果与理论值差异显著,而伪声抑制方法能有效过滤涡波伪声源,CFW-H 数值解与理论值保持一致。
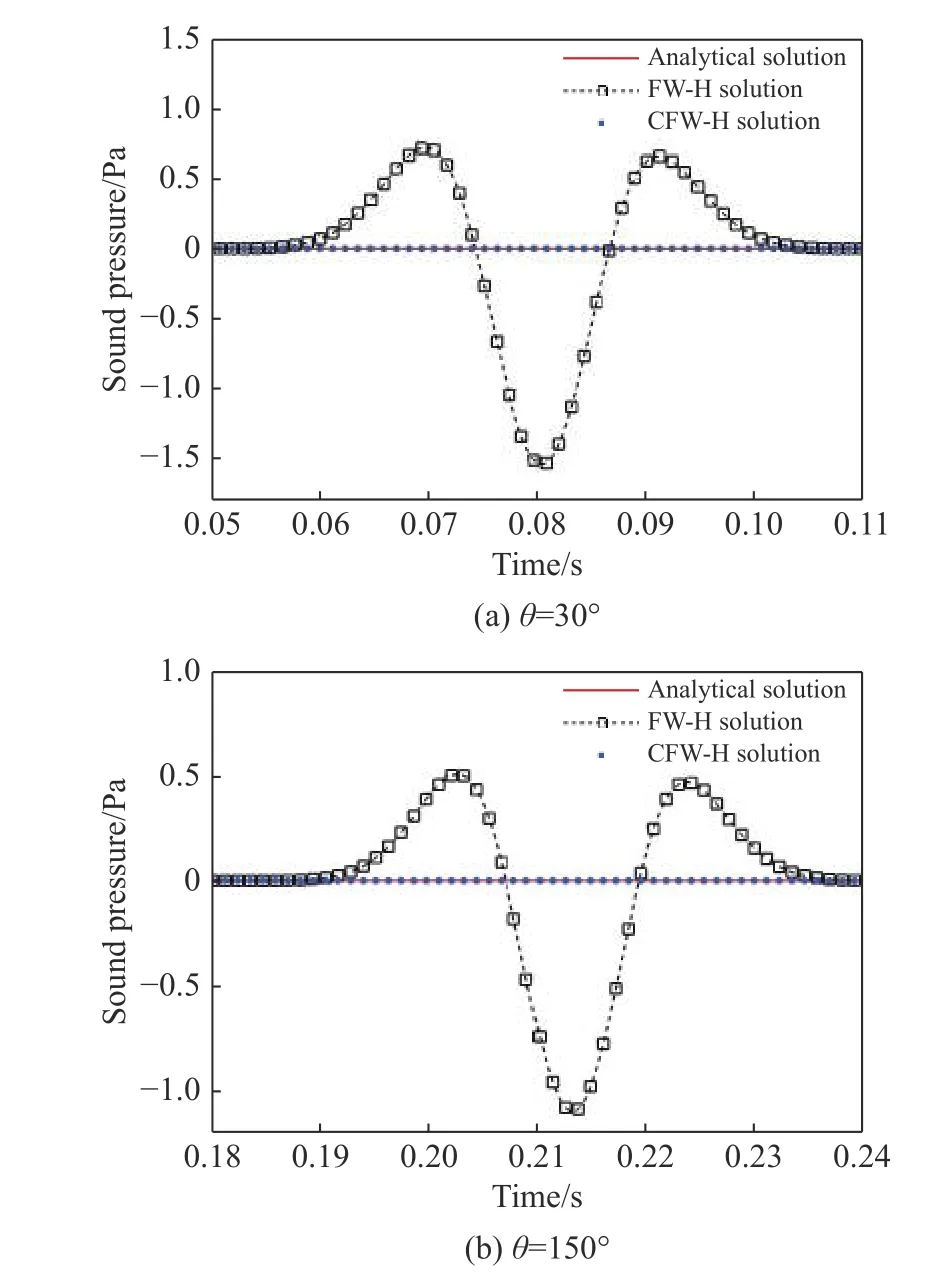
图6 对流涡伪声时间历程Fig.6 Time histories of spurious noise induced by a convective vortex
3.3 均匀流中的单极子与对流涡
考虑均匀流中同时存在静止单极子和恒速运动对流涡的情况。将单极子诱导的压力和密度,以及单极子和对流涡诱导的速度扰动和,作为可渗透面的流动参数(假设仅在 S4面存在涡波扰动),将其输入程序代码预测噪声传播。因对流涡诱导的压力场不会传播到远场,观察点的声场理论上仅含单极子贡献。不考虑声波与涡波间相互作用,即忽略厚度源和载荷源中的非线性项,仅考虑一阶线性扰动项对声学远场的贡献。图7(a)和图7(b)分别为 θ=30◦和 θ=150◦处声场预测结果。FW-H 数值解在涡波通过 S4面时产生了显著的伪声辐射,且受均匀流的对流效应影响,点源下游的伪声污染比上游更加强烈。CFW-H 数值解与理论解很好地吻合,证明了涡波伪声产生机制的正确性和抑制方法的有效性。
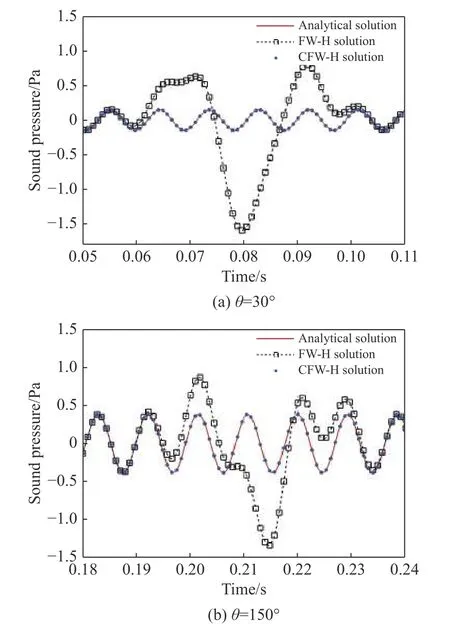
图7 静止单极子和对流涡诱导的声压时间历程Fig.7 Time histories of acoustic pressure induced by a stationary monopole and a convective vortex
需要指出的是,如果可渗透面处存在强烈的涡-声和涡-涡非线性相互作用,CFW-H 数值解仍将产生明显的数值误差。不妨考虑 S4面上因对流涡运动诱导的压力扰动和密度扰动,解析表达式为:
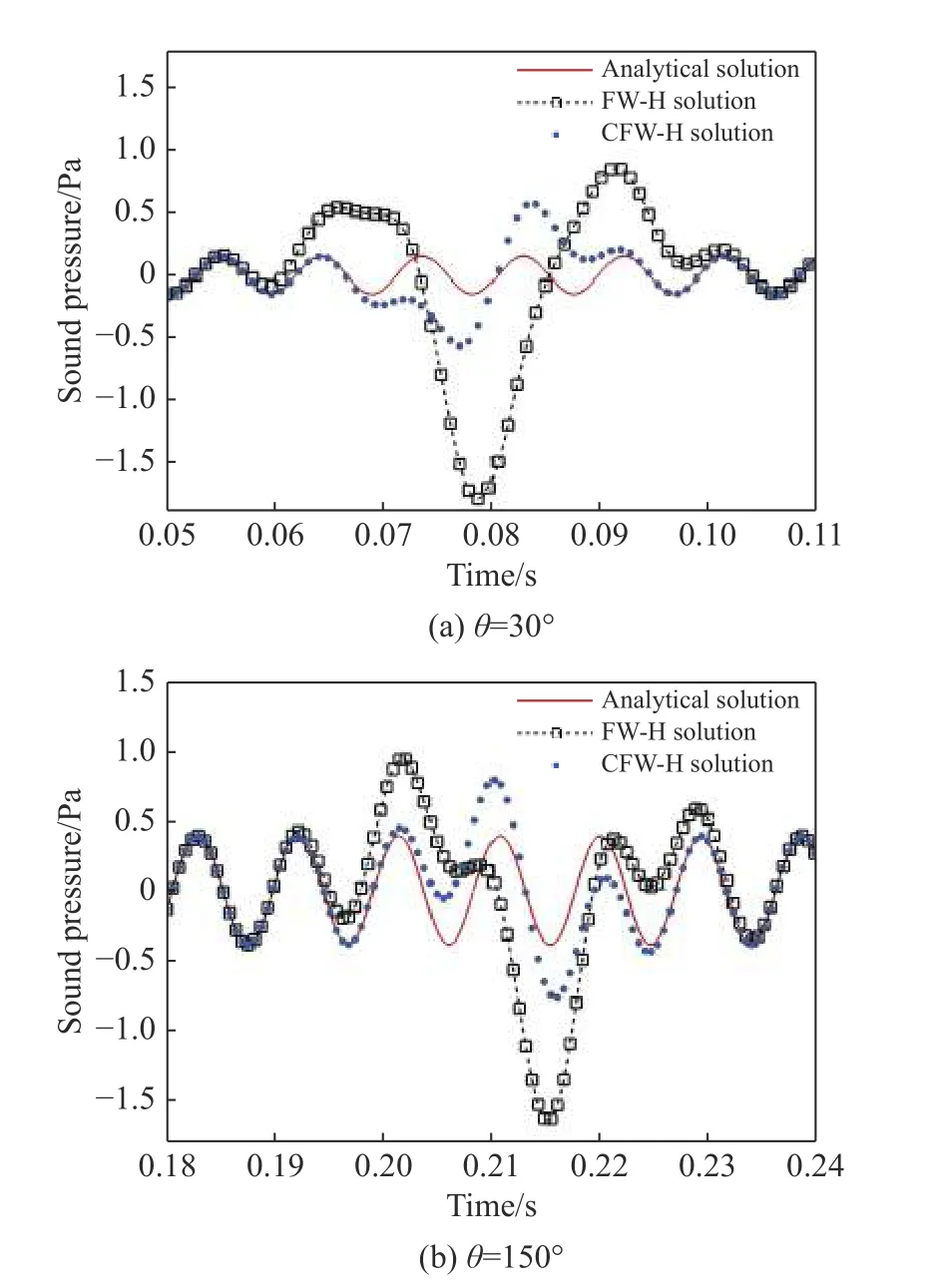
图8 计入对流涡压力和密度扰动影响的声压时间历程Fig.8 Time histories of acoustic pressure time accounting for the pressure and density fluctuations induced by the convective vortex
4 结论
可渗透面对流FW-H 方程右端源项包含了单极子厚度源、偶极子载荷源和四极子体积源。虽然缓慢衰减的涡波穿过可渗透面后沿平均流向下游传播,但由于体积源项不含有伪声源,只要主要声源被可渗透面包围,忽略体积源的远场贡献仅会产生数值误差,而不会诱发涡波伪声辐射,因此可渗透面急剧截断空间积分区域不是产生涡波伪声的根源。尽管厚度源的物质导数和载荷源的散度操作不能分别过滤伪厚度源和伪载荷源,但两者的耦合作用可自动过滤伪声源。伪声产生的真正原因在于对流FW-H 方程的求解采用了Farassat 提出的分部积分公式,部分积分项被忽略,从而导致伪声源自动过滤功能失效。如果直接利用流动数值模拟所得扰动速度计算积分面厚度源参数Q和载荷源参数L,对流FW-H 方程积分公式就引入了涡波伪声辐射。
将对流FW-H 方程进行恒等变形,从厚度源和载荷源中抽取含有涡波扰动的项,在对流波动方程求解过程中保留相应的物质导数和散度操作,即可过滤涡波伪声源,从而实现涡波伪声传播的有效抑制。根据这一思想,发展了修正的时域和频域声学积分方程。对均匀流中的单极子和对流涡算例,利用时域积分解讨论了涡波伪声抑制方法的可靠性。数值结果显示,FW-H 积分方程数值解在涡波通过可渗透面时间产生了显著的伪声辐射,且受均匀流对流效应影响,点源下游的伪声污染比上游更强烈;修正后的数值解与理论解相吻合,验证了伪声产生机制分析的正确性。
本文关注涡波伪声的产生机制,但仅研究了具有理论解的简单算例,后续将利用三维复杂流动算例开展进一步的时域与频域验证工作。此外,本文伪声抑制方法也适用于近场预测,只是文中没有给出相应的验证结果。
