基于符号补偿的RISC-V处理器乘法器优化
2023-08-03高嘉轩刘鸿瑾张绍林华更新
高嘉轩,刘鸿瑾,施 博,张绍林,华更新
(1.北京控制工程研究所,北京 100190;2.北京轩宇空间科技有限公司,北京 100080)
0 引言
目前嵌入式领域主要应用的处理器为ARM架构处理器,然而该架构经过多年的研究与扩展,其实现逐渐变得复杂。同时,ARM架构需要高昂的授权费,导致应用开发成本增高,不利于进行自主扩展开发。而RISC-V是由加州大学伯克利分校提出的一个开源指令集架构,其特点是开源、简单、可扩展等,具有良好的内部结构[1]。其高度模块化的指令集架构可应用于各种需求的处理器设计[2]。出于自主可控的考虑,开源的RISC-V架构将成为处理器开发的新方向。作为一种新兴的开源指令集架构,RISC-V已经在学术界和工业界都得到了广泛的关注[3]。RISC-V生态系统的开源社区为其提供了丰富的对应工具链与开源软件,使研究者们能够在研究中快速利用RISC-V[4]。基于RISC-V官方指令集手册,已发布了多款RISC-V处理器[5],比如Rocket Core[6]、SiFive[7]、BOOM Core[8]和LowRISCSoC[5]。
乘法器是处理器的运算核心,其运行速度影响了处理器的运行速度[9]。许多数字信号处理和机器学习应用需要进行大量乘法计算,其表现在很大程度上受到乘法器性能的限制。以卷积神经网络为例,超过90%的CNN计算为乘法累加计算[10]。因此面对嵌入式领域乘法算力需求较高的应用场景,研究开源指令集架构的RISC-V乘法器算力与功耗优化十分必要。乘法器主要包括三个阶段:操作数相乘产生部分积、部分积累加产生两个结果以及两个结果相加产生最终结果。目前整型乘法器的算法设计主要有串行累加阵列、Booth编码和Wallace树型结构[11]。针对Booth编码的研究,通过改进后的4位编码加快了对部分积最低位的获取,但编码位数更多,逻辑更为复杂[12]。而缩减基4-Booth编码位数,则无法对最低位获取进行优化,浪费了芯片面积[13]。有研究采用了符号扩展,从而减少了资源消耗,但未考虑部分积累加时的压缩[14]。而针对Wallace树型结构,有研究表明仅由基本压缩器构成 Wallace 树结构,需要经过5级压缩才能将9个部分积压缩为2个结果,其运算效率十分低下[15]。文献[16]对Wallace树型结构进行了改进,缩短了压缩延时,解决了蜂鸟E203部分积压缩延时大的问题,但其未考虑有符号部分积扩展带来的损失。对压缩器的研究主要是对其硬件结构进行研究,通过传输门结构设计基本压缩器,节省了压缩器面积,但不能实现双轨输出[17]。而高阶压缩器可以由多个基本压缩器串联形成,但关键路径上门数较多,延时较长影响压缩器性能[18]。
为了在不提升处理器功耗的前提下,提高RISC-V乘法器算力,减少进位次数,压缩延时,本文提出了一种基于符号补偿、基4-Booth编码以及Wallace树型结构的优化乘法器。由于基4-Booth编码的系数存在负数,在压缩时,需要进行符号扩展补齐,负数部分积累加时将产生大量进位以及比特翻转。针对该问题,本文提出了基于符号补偿的基4-Booth编码,有效压缩了负数符号扩展时连续比特1,减少了在加法时造成的进位以及比特翻转,降低了乘法器功耗。传统Wallace树型结构由于硬件压缩器功能简单,因此其层次过多,关键路径过长,结构不对称。针对该问题,本文提出了交替使用3-2压缩器与4-2压缩器的Wallace树型结构。改进后的Wallace树型结构对称,有效减少了树型结构的层次,缩短了关键路径的长度,压缩了累加过程的延迟,降低了乘法指令执行延迟,提高了处理器乘法算力。同时由于压缩器阶数不高,因此对电路复杂度以及延迟未有明显影响。本文从仿真、综合以及板级层面对其进行了功能性验证以及性能评估,测试结果表明,与未改进的PicoRV32相比,使用改进乘法器的PicoRV32在功耗有所降低的情况下,乘法器性能得到了显著提升。
1 RISC-V指令集架构
作为一种新兴指令集架构,RISC-V架构在设计之初总结了传统指令集的优缺点,避免了传统指令集的不合理设计。RISC-V指令编码简单,并且为扩展指令集预留出了足够的编码空间。RISC-V指令主要分为6个类型[19],包括:R型指令:寄存器-寄存器操作;I型指令:短立即数和访存load操作;S型指令:访存store操作;B型指令:条件跳转操作;U型指令:长立即数操作;J型指令:无条件跳转操作。各个类型指令结构如图1所示。
其中,opcode为操作码,表示指令操作。funct3和funct7部分作为opcode的附加字段,和opcode共同决定指令的具体操作。rs1和rs2表示两个源操作数的寄存器编号,rd表示目的操作数的寄存器编号。该编码结构位置固定,便于译码模块对指令进行解析。
RISC-V指令集的整数乘法指令共有4条,分别为MUL、MULH、MULHSU、MULHU,均为R型指令。指令具体描述及用法如表1所示。
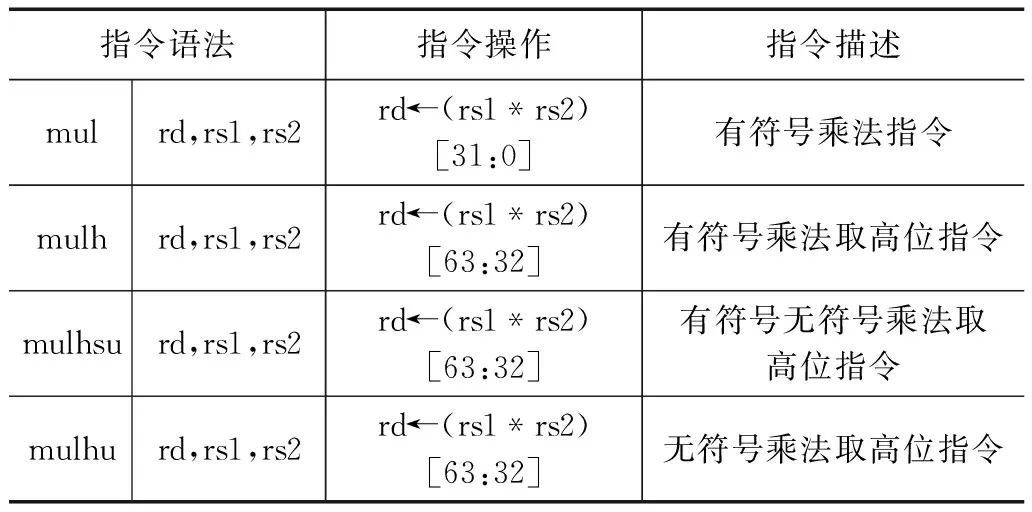
表1 RISC-V乘法指令表
其中MUL指令将源操作数进行符号位扩展,选取计算结果的低32位,MULH指令将源操作数进行符号位扩展,选取计算结果的高32位,MULHSU指令的源操作数rs1为有符号数,rs2为无符号数,指令结果选取计算结果的高32位,MULHU指令将源操作数进行零扩展,选取计算结果的高32位。
2 基4-Booth编码
1951年,A.D Booth 在其论文“A Signed binary multiplication technique”中提出一种快速乘法算法——Booth算法[20],即为了解决有符号乘法运算中复杂的符号修正问题而提出一种乘法算法,将乘数转变数据表示形式,使其数据出现尽可能多的0,其编码原理如式(1)所示。
y=2n-1(-yn-1+yn-2)+2n-2(-yn-2+yn-3)+
2(-y1+y0)+(-y0+y-1)
(1)
式中,y为乘数,n为乘数位数,yn-1为y的n-1位。
从式(1)可以看出,基础Booth编码并不能在硬件乘法器电路中起到真正的优化作用,实际部分积个数并未减少。因此在基2-Booth编码的基础上提出了改进的Booth编码,即基4-Booth编码,进一步减少部分积个数,从而达到减少硬件加法器的目的,其编码原理如式(2)所示。
y=2n-2(-2yn-1+yn-2+yn-3)+
2n-4(-2yn-3+yn-4+yn-5)+
22(-2y3+y2+y1)+(-2y1+y0+y-1)
(2)
式中,y为乘数,n为乘数位数,yn-1为y的n-1位。
从式(2)可以看出,多项式的项数相较于式1减少了一半,因此通过基4-Booth编码可以有效减少部分积的个数。
然而基4-Booth编码的系数存在负数的情况,以2n-2项系数为例,当yn-2=0,yn-3=0且yn-1=1时,该项系数为-2,因此需要考虑负数部分积对压缩的影响。由于部分积位数不同,在压缩时,需要进行符号扩展进行补齐,当部分积为负数时,符号位补齐为1,累加时将产生大量进位以及比特翻转,增加乘法器功耗。
3 Wallace树型结构
基4-Booth编码优化了整型乘法中部分积的数量,从而减少累加次数。而为了进一步减少累加操作产生的延迟,1964年,C.S.Wallace提出的一种高效快速的加法树结构,被后人称为Wallace树[21],其核心思想为将每3个加数分为一组,压缩至2个加数,即计算结果与进位,循环往复,最终得到累加结果,其结构如图2所示。
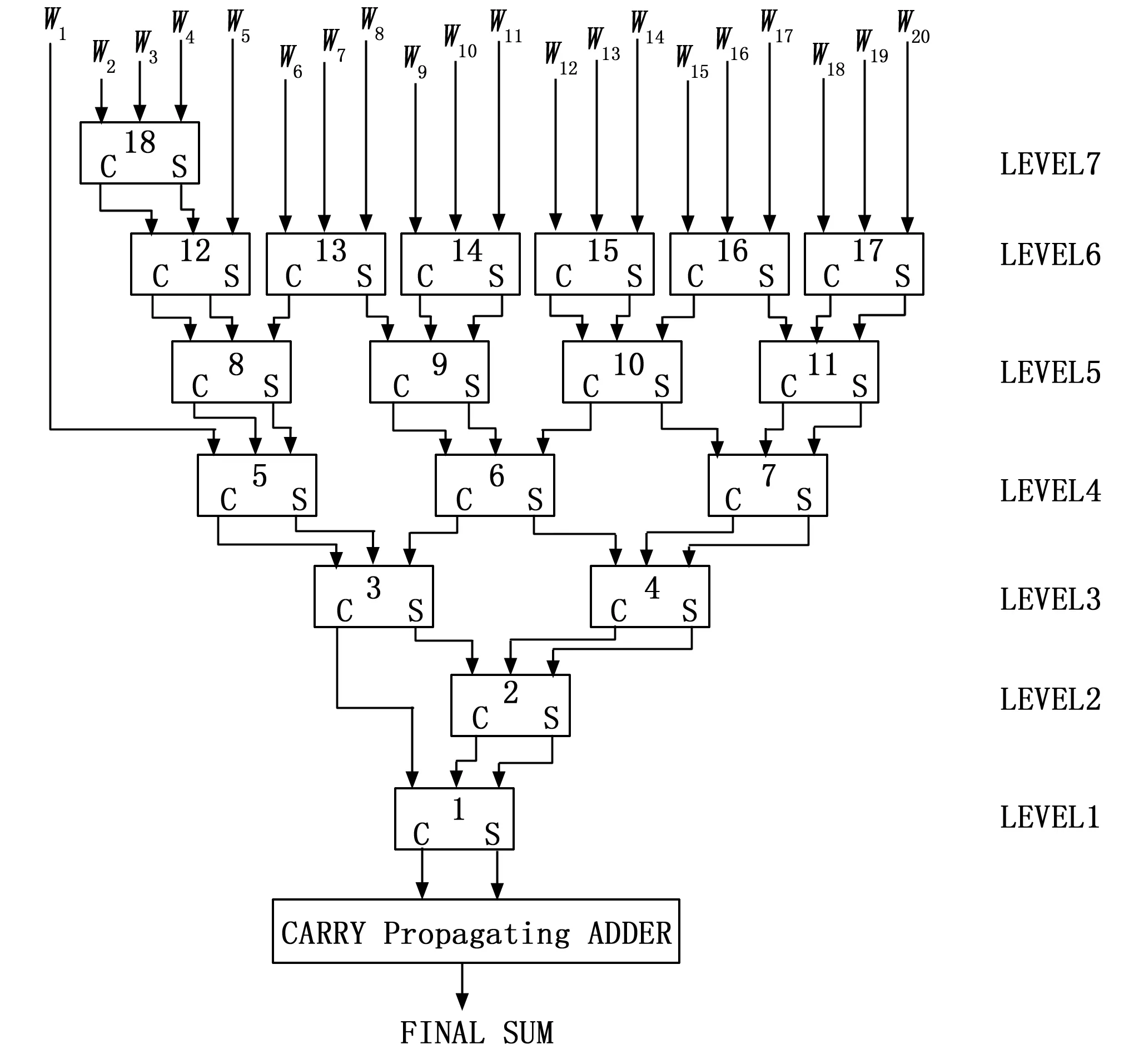
图2 Wallace树型结构图
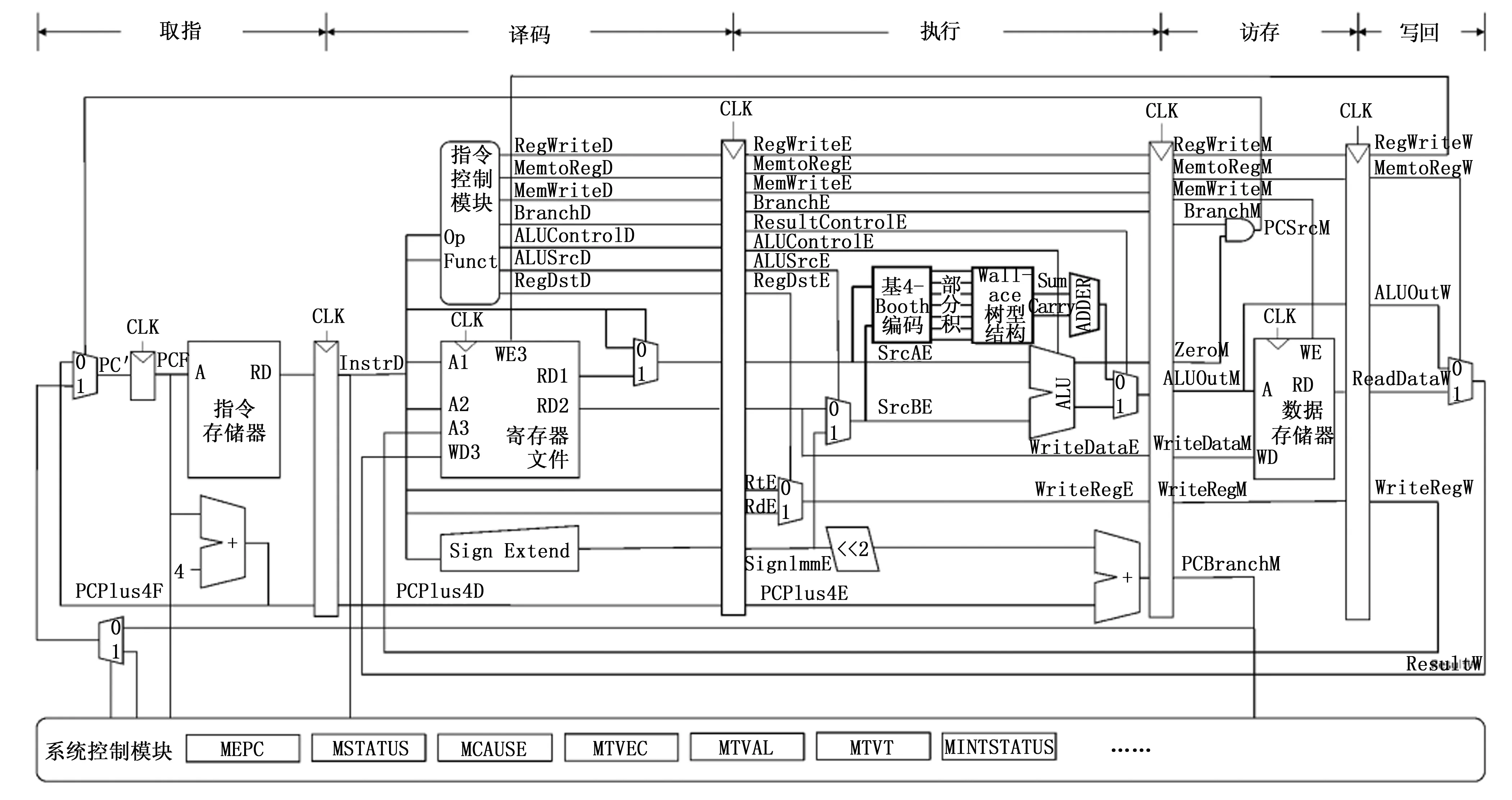
图3 RISC-V处理器结构图
Wallace树型结构提高了累加操作的执行并发性,通过树型结构提高了硬件压缩器的复用性,缩短了关键路径的长度,有效地缩短了累加操作的执行时间。
然而传统Wallace树型结构由于硬件压缩器功能简单,其层次依旧过多,并且对于32位数据计算,其结构不对称,增加了电路的复杂度,消耗了更多布线资源。不规则的布局布线结构,增大了关键路径的时延。随着硬件压缩器的不断发展,Wallace树型结构可通过使用高阶压缩器实现进一步优化。而阶数过高的压缩器,例如7-3压缩器、6-3压缩器存在电路设计复杂、硬件占用资源多、功耗高以及面积大等问题,因此面对嵌入式领域对低功耗的需求,需要在控制乘法器功耗以及面积的情况下,优化Wallace树型结构,从而提高乘法器算力。
4 乘法器优化设计
本文设计的乘法器用于单发射顺序执行五级流水线RISC-V处理器32×32位有符号整数乘法运算,主要模块包括:通过改进的基4-Booth编码产生部分积,通过改进的Wallace树型结构对部分积进行压缩。RISC-V处理器结构图以及乘法器的结构图如图3所示。
在处理器五级流水线结构中,乘法器位于执行阶段,译码模块从指令中解析出被乘数与乘数,通过改进的基4-Booth编码产生部分积,部分积阵列通过Wallace树型结构计算出累加结果和进位两个数据,最后通过加法器计算出最终结果,通过多选器根据指令功能选取对应的结果位。
本文对基4-Booth编码进行改进,将补码计算以及符号位扩展与基4-Booth编码相结合,减少符号位扩展对压缩效率的影响。对Wallace树型结构进行改进,加入4-2压缩器,使改进的Wallace树型结构对称,减少其层次数量,缩短关键路径长度。部分积阵列经过改进后的Wallace树型结构,产生两个结果,通过全加器得到乘法计算结果。
4.1 改进的基4-Booth编码
基4-Booth编码减少了部分积的数量,其中存在负数部分积,而当部分积为负数时,符号位补齐为1,累加时将产生大量进位以及比特翻转,增加乘法器功耗。针对该符号位问题,有研究提出了一种有效的符号补偿方式[22],有效减少了符号位扩展以及补码引起的功率消耗。采用符号位直接扩展时,以8位数据snXXXXXXX为例,其中sn表示符号位,将其扩展为16位数据,其结果为sn sn sn sn sn sn sn sn snXXXXXXX。而使用该符号补偿方式,可对其进行等价逻辑变换,如式(3)所示:
snsnsnsnsnsnsnsnsnXXXXXXX=
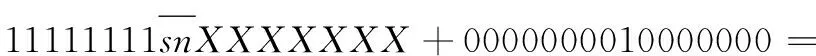
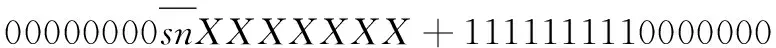
(3)
从式(3)可以得出,由于符号位扩展部分为连续相同的数据,因此根据二进制计算特点,可将符号扩展变换为只与符号位及固定值有关的运算,而固定值可提前根据部分积数量以及位数进行计算,其计算结果可在部分积累加前通过编码实现。因此本文通过将该符号补偿方式、补码计算与基4-Booth编码相结合,形成改进后的基4-Booth编码,扩展方式如图4所示。
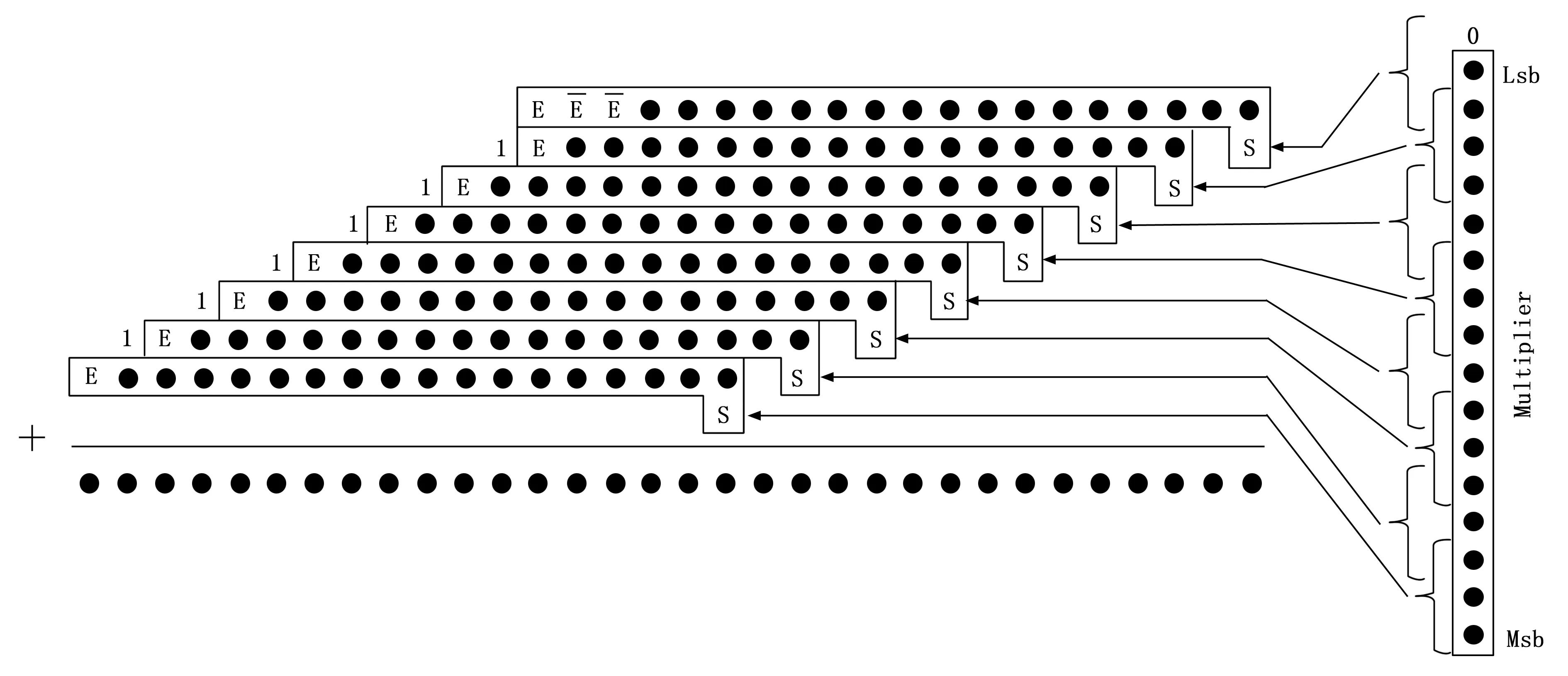
图4 改进符号扩展图

本文在基4-Booth编码的基础上,加入对符号补偿以及补码的编码,从而将上述符号补偿方式与基4-Booth编码相结合,减少部分积压缩的功率消耗。本文采用如表2所示的编码。

表2 改进的基4-Booth编码表
表中y2i+1y2iy2i-1代表乘数的第2i+1、2i和2i-1位,对于32位处理器,i的范围为0到16;Coefi代表第i个部分积系数;E代表乘上系数后的符号位,sn代表被乘数的符号位;S代表补码加1操作产生的中间值,本级的中间值拼接至下一级部分积,在压缩过程中实现补码计算。改进的基4-Booth编码电路图如图5所示。
其中:Y_2i+1、Y_2i和Y_2i-1代表y2i+1y2iy2i-1,即乘数的第2i+1、2i和2i-1位,sign代表Coefi的符号,coef1代表Coefi[1],coef0代表Coefi[0],E代表被乘数符号位的系数,S1代表中间值S[1],S0代表中间值S[0]。

图5 改进基4-Booth编码电路图
从图5可以看出,改进的Booth编码通过与门、或门、非门以及二选一多选器实现,经过4个门的时间延迟即可得出编码结果。
根据Coefi的编码结果,分别对被乘数进行相应操作。对于系数为负数的部分积,对被乘数进行按位取反,对于系数绝对值为2的部分积,对被乘数进行左移1位操作。将乘以系数的部分积与编码后的符号位以及中间值进行拼接,形成改进后的部分积,该部分积阵列输入Wallace树型结构进行累加计算。
采用基于符号补偿的基4-Booth编码,不需要扩展全部符号位,减少了由于扩展大量连续的1,在加法时造成的进位以及翻转,降低了乘法器功耗。
4.2 改进的Wallace树型结构
基础的Wallace树型结构采用3-2压缩器,通过树型结构有效提高累加操作的并行性,同时从硬件设计角度,增加了加法器的复用性,减少了硬件加法器的数量。为了更好地配合32位处理器的运算需求,在不提高处理器功耗的情况下,尽可能减少Wallace树型结构的层次,提出了一种交替使用3-2压缩器与4-2压缩器的Wallace树型结构,改进后的Wallace树型结构示意图如图6所示。

图6 改进的Wallace树型结构图
由于使用符号补偿方式,32位操作数将产生17个部分积,因此为了使Wallace树型结构对称,将32位乘法运算经过符号扩展,产生18个部分积,18个部分积经过3-2压缩器产生12个操作数,再经过4-2压缩器产生6个操作数,6个操作数经过3-2压缩器产生4个操作数,在经过4-2压缩器产生最终的2个结果。
其中3-2压缩器的逻辑表达式如式(4)~(5)所示:
S0=X0⊕X1⊕X2
(4)
C1=X0X1+X0X2+X1X2
(5)
式中,S0为第0个3-2压缩器的压缩结果,C1为第0个3-2压缩器的进位结果,X0、X1和X2为3-2压缩器的3个输入操作数。
其1位电路示意图如图7所示。
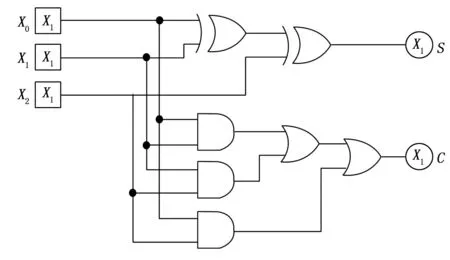
图7 3-2压缩器1位电路图
从图7可以看出,3-2压缩器仅使用与门、或门和或非门构成,经过3个门的时间延迟即可得出结果。
4-2压缩器,又称5-3计数器,包括5个输入和3个输出,输入和输出分别包括一个进位。传统的4-2压缩器是由两个串行连接的3-2压缩器组成,而改进后的4-2压缩器可以通过异或门和2-1的多选器构成,改进后的4-2压缩器的逻辑表达式如下所示:
Cout=X0X1+X0X2+X1X2
Xor=X0⊕X1⊕X2⊕X3
S0=Xor⊕Cin
式中,S0为第0个4-2压缩器的压缩结果,C1为第0个4-2压缩器的进位结果,Cout为同级4-2压缩器的进位结果,X0、X1、X2和X3为4-2压缩器的4个输入操作数。
由于Cout的逻辑表达式与Cin无关,所以4-2压缩器之间虽有信号连接,但不会形成行波进位链,4-2压缩器之间依旧是并行的,其结构示意图如图8所示。
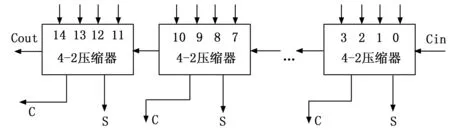
图8 4-2压缩器结构图

图9 乘法指令波形图
采用3-2压缩器和4-2压缩器交替的Wallace树型结构对称,减少了布局布线资源,有效减少了树型结构的层次,缩短了关键路径的长度,压缩了累加过程的延迟。同时,使用的3-2压缩器和4-2压缩器电路简单,电路最大延时短,未造成处理器功耗以及面积大幅提高。
5 实验结果与分析
本文的实验环境如表3所示。

表3 实验环境表
采用Verilog语言对设计的32位乘法器进行实现,并嵌入到PicoRV32中,通过汇编语言对乘法器进行功能仿真,将结果与Spike仿真结果进行对比验证乘法器功能的正确性。
图9为乘法器执行乘法指令的仿真波形,其结果与Spike仿真的结果一致。
从图9可以看出,通过MUL指令计算32’habcde与32’habcde相乘,其计算结果为32’h4caed084,与预期结果相符。通过如下所示代码,对其余指令以及边界值进行验证。
.global MUL
MUL:
li x3, 0x80000000
li x4, 0x7fffffff
li x10, 0xabcde
mul x5, x0, x3
bne x5, x0, __fail
mul x5, x0, x0
bne x5, x0, __fail
mul x5, x0, x4
bne x5, x0, __fail
mul x5, x4, x4
li x6, 0x1
bne x5, x6, __fail
mul x5, x4, x0
bne x5, x0, __fail
mul x5, x4, x3
li x6, 0x80000000
bne x5, x6, __fail
mul x5, x4, x10
li x6, 0xfff54322
bne x5, x6, __fail
mul x5, x3, x3
li x6, 0x0
bne x5, x6, __fail
mul x5, x3, x0
bne x5, x0, __fail
mul x5, x3, x4
li x6, 0x80000000
bne x6, x5, __fail
mul x5, x3, x10
li x6, 0x0
bne x6, x5, __fail
mul x5, x10, x10
li x6, 0x4caed084
bne x6, x5, __fail
上述代码对32位操作数的最大正值0x7fffffff、最小负值0x80000000、中间值0xabcde以及0进行乘法计算,通过对乘法器计算结果的判断,进行程序跳转,从而测试指令执行结果是否正确。当指令结果正确,即符合预期时,程序顺序执行,仿真成功结束。当指令结果不正确时,程序跳转至__fail,表示程序执行错误,仿真错误结束。其余3条乘法指令与MUL指令测试程序相同。如图10所示,测试结果为仿真成功结束,表明指令执行结果正确,即设计的乘法器功能正确。
图10 乘法指令测试结果图
通过图9波形图,本文的乘法器接收到乘法指令,第一个时钟周期计算累加结果以及进位,第二个时钟周期两者相加得出最终结果,因此乘法所需时钟周期为2个时钟周期。为了更加直观地体现本文乘法器的性能,将优化后的乘法器与PicoRV32乘法器以及文献[16]进行了性能对比,结果如表4所示。

表4 乘法器时钟周期数对比表
从表4可以看出,与文献[16]相比,本文的乘法器执行乘法运算花费的时钟周期数相同。而相较于PicoRV32乘法器,本文改进后的乘法器大幅减少了乘法计算所花费的时钟周期数,乘法指令执行时间缩短了88.2%,减少了乘法指令的执行延迟,提高了处理器的算力。
本文使用Synopsys公司的Design Compiler软件,基于smic40nm工艺库,对乘法器进行了综合,对其面积进行了评估,结果如表5所示。

表5 乘法器面积对比表
从表5可以看出,由于扩展了基4-Booth编码以及使用了4-2压缩器,本文乘法器相较于PicoRV32原乘法器在面积上增加了13.3%。而与文献[16]乘法器相比,本文乘法器在面积上优于文献[16],减少了10.6%。从表4可以得出,本文乘法器与文献[16]乘法器执行乘法指令时钟周期数相同,因此本文设计优化的乘法器优于文献[16]。
Dhrystone可对处理器的整型运算性能进行测量。因此本文通过运行测量处理器运算能力的基准程序之一的Dhrystone,在板级对带有本文乘法器的RISC-V处理器进行了进一步性能与功耗测试,其性能与PicoRV32对比如表6所示。

表6 处理器性能对比表
从表6可以看出,与PicoRV32相比,本文设计的乘法器在算力方面提高了71.7%,而处理器算力提高的同时,处理器功耗降低了4.9%。文献[16]提升了处理器算力,但处理器功耗也有所提高,而本文的乘法器与其相比,算力有所提高,功耗有所降低,提高了处理器的能耗比。
6 结束语
本文通过对RISC-V架构中整数乘法指令的研究以及乘法器的研究,提出了基于符号补偿的基4-Booth编码以及使用3-2压缩器和4-2压缩的改进Wallace树型结构,设计实现了改进后的RISC-V处理器乘法器。通过RISC-V汇编语言对改进后的乘法器进行功能仿真,验证了其功能正确性。使用Design Compiler软件对乘法器面积进行了综合,与处理器原乘法器以及已有工作进行了对比分析。通过板级测试,对处理器算力以及功耗进行了评估,并与原处理器以及已有工作进行了对比分析。结果表明,本文改进的乘法器功能正确,执行整型乘法指令所花费的时钟周期为2,相较于PicoRV32乘法器,缩短了88.2%。Dhrystone分数为2.115 728 DMIPS/MHz,功耗为0.035 42 W,相较于未改进的PicoRV32,性能提高了71.7%,功耗降低了4.9%,在功耗有少许降低的情况下,大幅提高了处理器性能,提高了处理器计算速度。与已有研究工作相比,本文改进的乘法器在执行乘法指令时钟周期数相同的情况下,面积与功耗均优于已有工作,适用于嵌入式领域对处理器面积、功耗以及算力有较高需求的应用场景。本文的乘法器确实在缩短整型乘法执行时间方面有一定效果,但在功耗方面优化并不明显,同时由于增加了符号扩展编码,乘法器面积有所增加,未来的改进方向为:
1)优化编码设计,尽可能降低编码逻辑复杂度;
2)考虑乘法器的低功耗优化。
