精密摆组件装配设备自标定方法
2023-08-03张建昆唐大林任同群曹润嘏王晓东
张建昆,唐大林,任同群,3,曹润嘏,吴 晗,王晓东,3
(1.微纳米技术及系统辽宁省重点实验室,辽宁 大连 116024;2.北京航天测控技术有限公司,北京 100041;3.高性能精密制造全国重点实验室,辽宁 大连 116024)
0 引言
摆式加速度计是惯性导航系统的重要核心器件,在航空航天、制导武器及机器人领域均有重要应用,其制造是否达标与摆组件的装配密切相关[1,2]。目前摆组件的装配多采用人工方法,装配效率、精度和一致性难以得到保证,为此,课题组开发了专用的摆组件装配设备。但装配设备各模块内部滑台之间存在安装误差,导致装配设备滑台移动的实际位置与理想位置之间存在偏差,装配精度难以得到保证。因此,需要对各滑台的相对位姿关系进行标定以进行误差补偿。
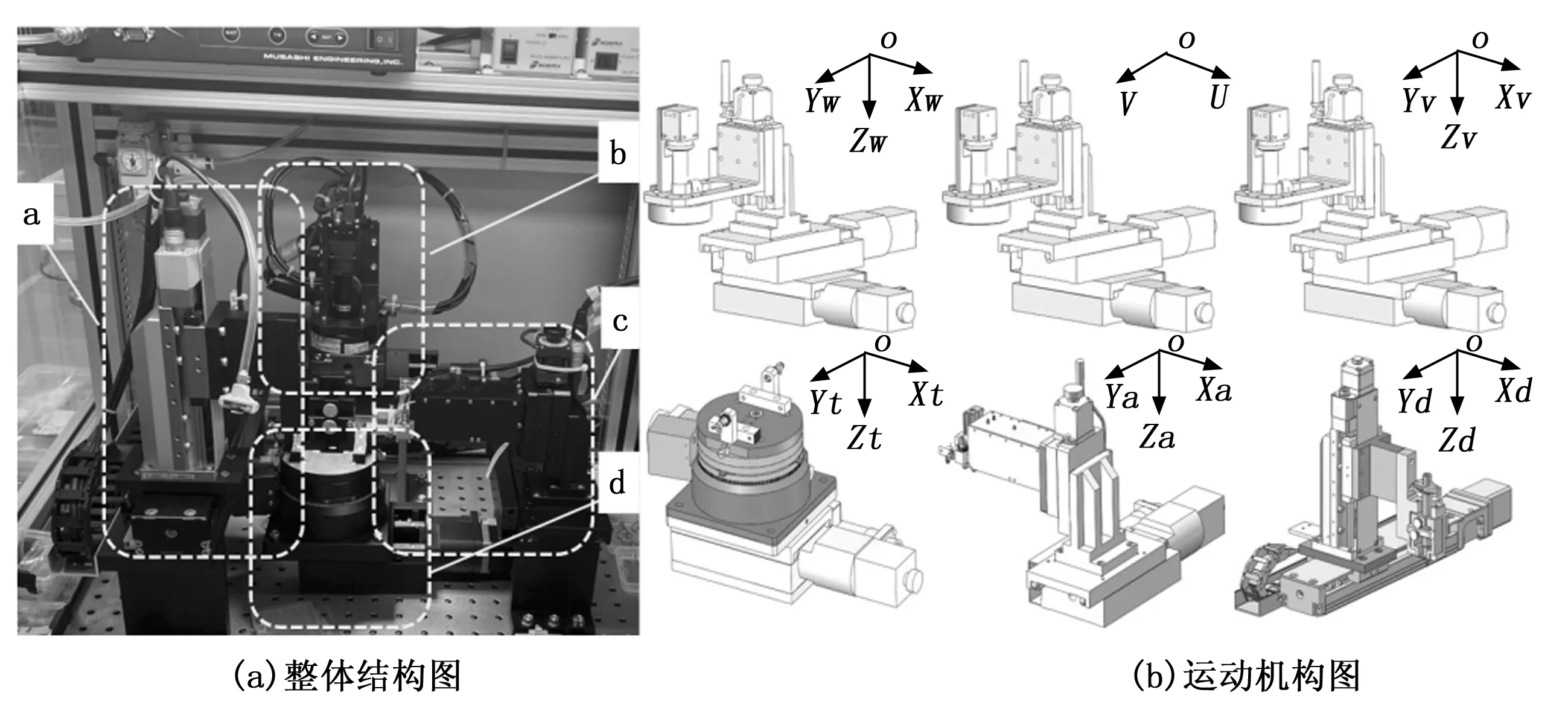
图1 精密微小摆组件装配设备
目前针对微装配设备的标定方法,主要包括传统标定和自标定[3]两种。前者在标定过程中需要借助外部设备进行数据检测,如激光跟踪仪、激光干涉仪等,因而具有成本高、操作复杂、便携性差等缺点[4-5]。后者不借助外部辅助测量设备仅通过自身传感装置,由运动学模型建立的约束方程进行参数计算求解误差[6-8]。该方法简单有效,方便快捷,更契合结构紧凑的微装配设备标定任务,也是目前的研究热点。Hage等[9]开发出一种自标定方法,通过建立执行机构与测量机构的约束方程求出了机器人的移动准确性,并根据理论模型给出了自标定算法。Matin等[10]提出一种由线性位移传感器和联轴器耦合成的自标定设备,可以对机器人在局部操作空间进行高精密的准确性测量。朱立伟[11]提出一种超精密二维工作台自标定模型,研究了随机误差在标定中的传递性并在此基础上建立超精密二维工作台自标定算法。Pan等[12]提出了一种线性结构光三维测量自标定方法,该方法将量子遗传算法和特征匹配应用于自标定得到系统参数的最优解。
以上自标定方法应用于微装配设备会存在标定时间长、自动化程度低、标定精度低等问题,为此课题组提出一种适用于部分微装配设备的标定方法[13],该方法自动化程度高,标定时间和精度均明显改善。但该方法还存在一些不足。首先,标定过程依靠特制的标定板,对于装配空间狭小的微装配设备而言,标定板的固定与安装较为困难,导致无法通用;其次,误差参数一般采用顺序标定,解算具有关联性,需要一种整体求解方法以克服由此带来的误差传递与累积问题;最后,在误差补偿验证实验中,该方法未将误差补偿模型中解算的脉冲带入滑台实际运动中,仅将该值与滑台在理论脉冲下运动的图像变化量进行对比,导致得到的结果不够直观。
综上,本文针对精密摆组件装配设备提出一种通用自标定方法。通过设备自身固有单一特征点识别代替特质标定板,仅由视觉系统跟踪特征点在装配作业空间中的若干任意点位,获取对应的位置与控制信息。然后,根据粒子群优化算法(PSO,particle swarm optimization)对误差参数进行整体求解,从原理上克服误差参数的解算关联性。最后,优化误差补偿验证方法,将补偿模型中解算的实际脉冲带入滑台运动中,得到直观可靠的验证结果。补偿模型中图像坐标与滑台运动脉冲一一对应,实现几何域到控制域的映射关系。
1 误差参数的标定
1.1 标定参数
精密摆组件装配设备的结构组成如图1(a),该设备的主要功能为实现摆组件器件各个组成零件之间的高精度装配,其中任务要求装配精度小于20 μm。摆组件装配设备采用模块化的设计方式,根据不同模块执行的任务不同,可划分为四个模块[14-15]。分别为a.点胶模块、b.视觉模块、c.装配作业模块和d.组装工作台模块等。各运动模块如图1(b)所示,采用右手定则对各个模块进行空间笛卡尔坐标系的建立。依次为:世界坐标系、图像坐标系、视觉坐标系、组装工作台坐标系、装配作业坐标系、点胶坐标系。其中;世界坐标系固定不动,与视觉坐标系初始位置重合。
摆组件的各个零件通过精密摆组件装配设备进行装配。零件上料任务时,首先移动载有相机的视觉模块滑台分别对组装工作台模块的上料区域位置特征和装配区域位置特征进行观测,其次将滑台移动的脉冲与相机镜头下的图像坐标向同一坐标系下转换,然后将组装工作台模块与装配作业模块的滑台移动脉冲也转化到上述同一坐标系下,最后通过移动组装工作台模块与装配作业模块滑台到相应位置完成装配。零件自动点胶过程类似,在此不再赘述。
为保证模块运动的准确性,需要对视觉模块、装配作业模块、组装工作台模块和点胶模块的滑台进行标定。坐标系的X轴和对应功能模块的X方向滑台重合,滑台存在安装误差,坐标系其余轴和滑台之间存在一定的误差偏角;同时坐标系之间也存在固定的偏转角,这些角度需要进行标定。图1(b)中各坐标系建立以后,需要对各坐标系进行刚体变换来确定误差参数。其中,世界坐标系固定不动,与视觉坐标系初始化后的原点位置重合,作为所有坐标系转换的中介,其他坐标系随滑台移动时刻变化。图像坐标系依托相机建立,相机通过转接板与视觉模块滑台固连,因此图像坐标系与视觉坐标系之间误差关系确定;各模块X向滑台和相应坐标系X轴方向重合,若模块无X向滑台,则使Y向滑台方向与坐标系Y向重合,标定其余滑台与对应坐标轴的误差角度参数,通过上述分析,各坐标系之间的误差角关系如图2所示,并总结得出如表1所示的摆组件设备需标定的误差参数。
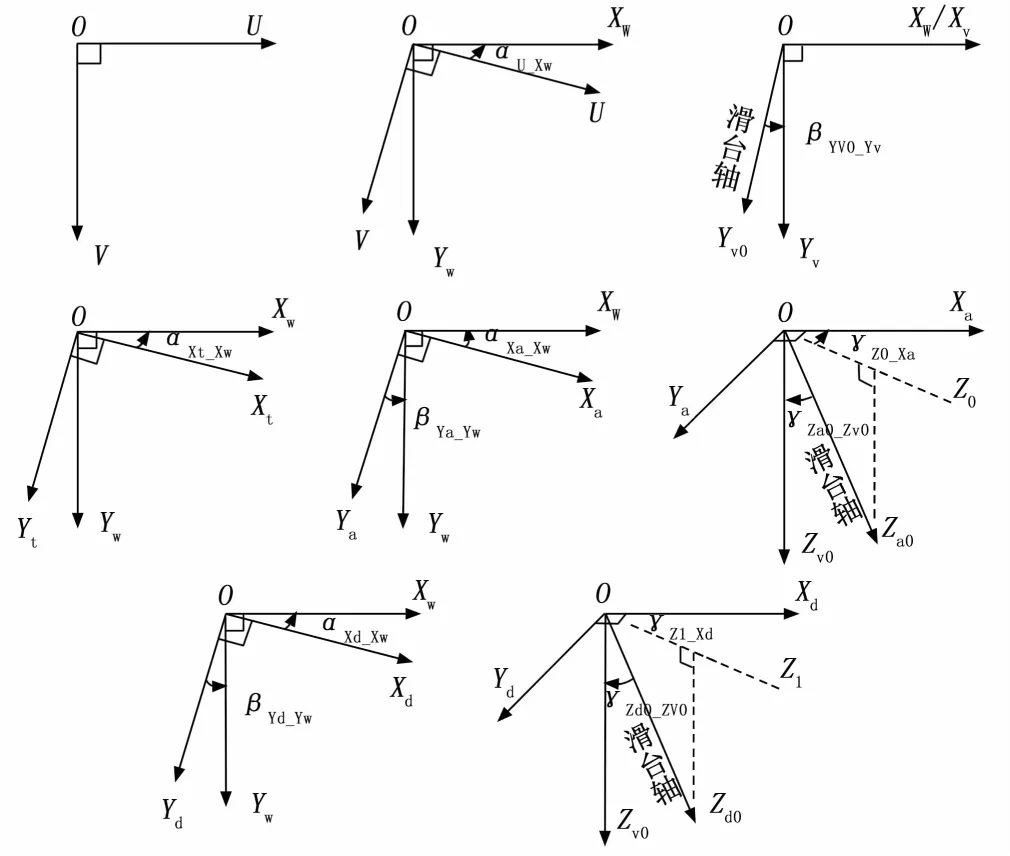
图2 误差角度参数
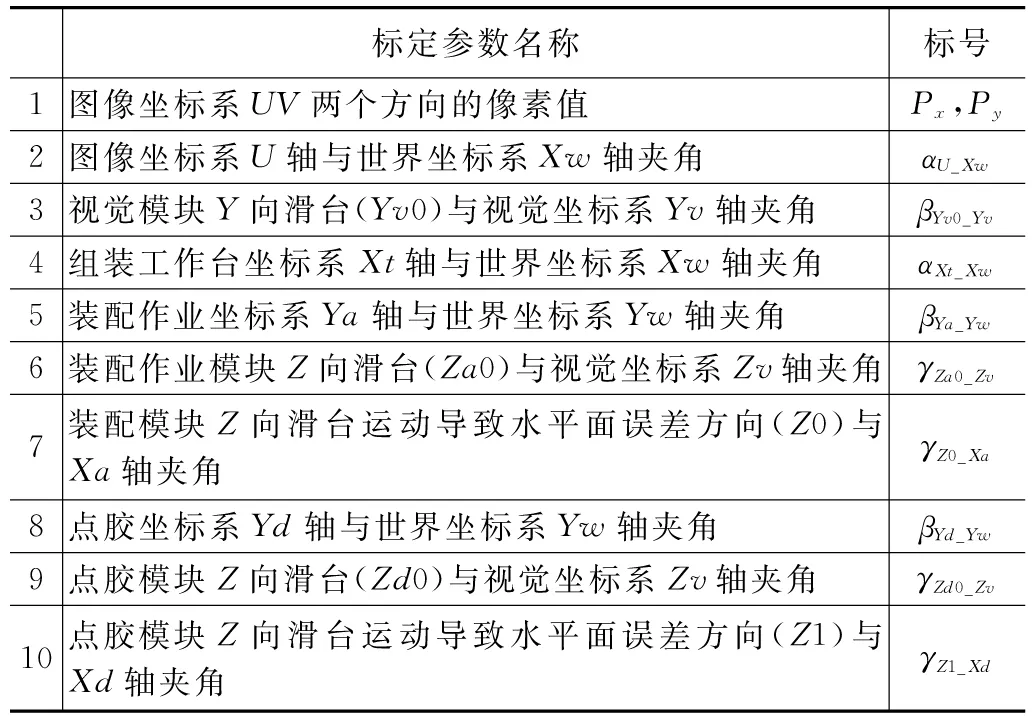
表1 摆组件设备需标定的误差参数
关于相机视觉测量特征点,目前微装配设备多采用标定板进行线性标定。线性标定的过程为视觉观测标定板上的用于图像识别的特征,通过滑台的移动使图像特征坐标发生变化,根据移动量与图像变化量带入解算模型中进行误差求解。但由于摆组件装配设备空间狭小,标定板需要固定且占据本就狭小的空间,导致标定板通用性较差。
由于不同设备工况不同,装配空间有限,部分设备如微小摆组件装配设备无法安装使用标定板。为此本文改进方法不再使用标定板,本文用相机观测零件和设备的特征代替标定板特征,进而使操作过程便捷,节约设计成本,提高了本方法的通用性,以装配模块为例,待标定零件吸附在机械臂的吸附头下方,其标定特征点为零件的方孔中心,相机测量标定特征点的示意图如图3所示。
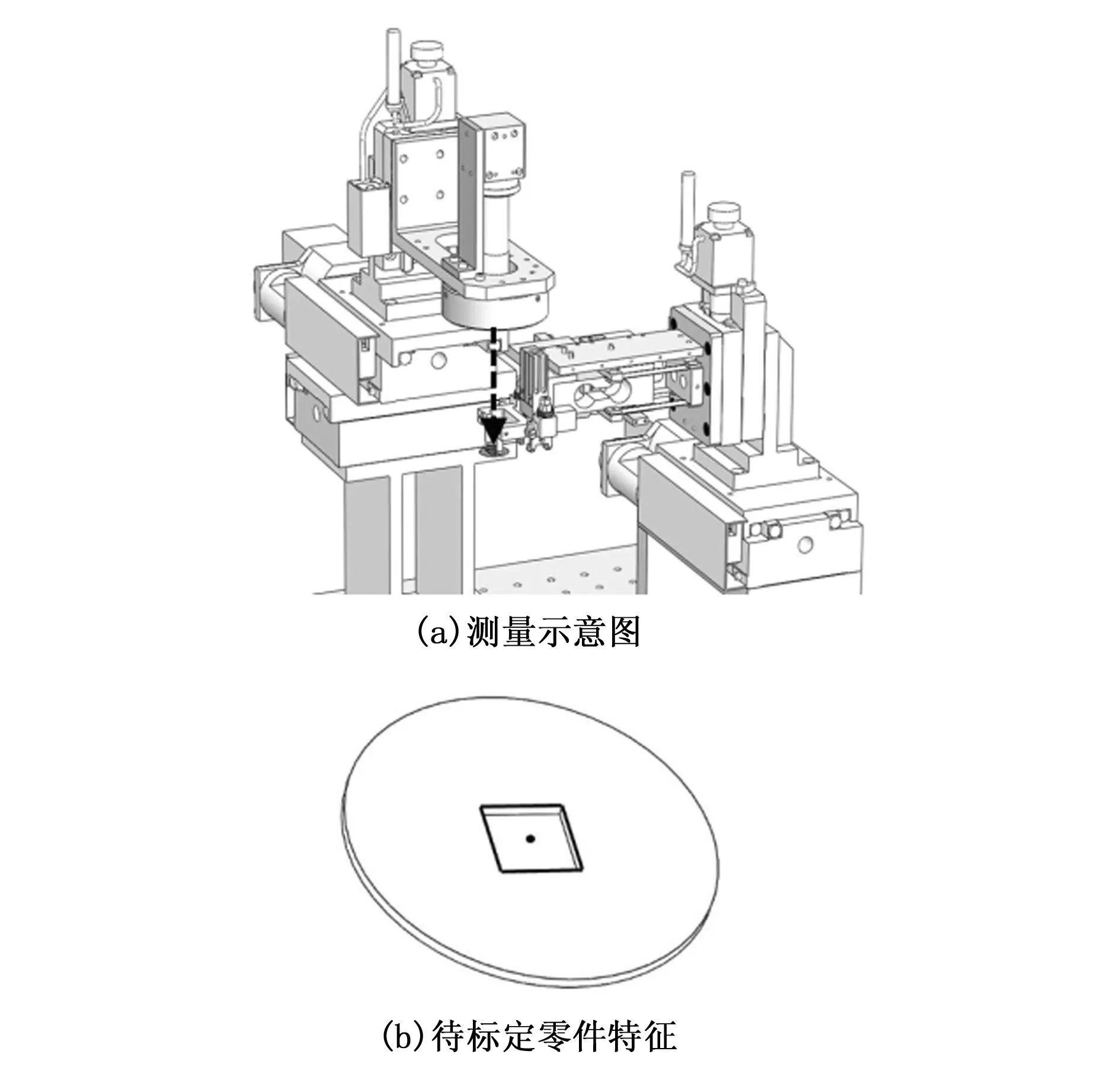
图3 标定特征点测量示意图
标定特征确认后,为满足标定方法,需确定标定参数在装配空间所需的标定点位。该标定点位的选取应充满整个装配空间,即可以是装配空间内的任意点位,为便于自动化流程且不失一般性,本文以空间中任意位置作为起始位置,控制滑台呈发射性向各个标定点位移动;装配模块与视觉模块除2个像素值误差参数之外,还需标定αU_Xw、βYv0_Yv、βYa_Yw、γZa0_Zv、γZ0_Xa这5个误差角度参数,因此至少需要5个标定点位才能求解误差参数。为保持解的稳定性,本文选取10个标定点位为标定方法提供数据以便进行误差参数的解算,具体介绍见第2章。
1.2 标定求解与误差补偿模型
求解了所有误差角度参数后,接下来根据误差参数将各坐标系进行整合成统一的误差补偿模型以便进行误差补偿。在此以图像坐标系的坐标变化及视觉滑台移动的实际脉冲向装配作业模块滑台移动的实际脉冲进行转换。本文采用的误差补偿模型,前人已做了详细的推导说明,本文只添加了相应的角度参数,对于误差补偿模型的推导不再赘述[13]。该模型由各模块坐标系与世界坐标系之间的旋转矩阵和各模块坐标系与自身滑台之间的补偿矩阵结合而成。如公式(1)所示,只需输入图像坐标变化量和滑台理论脉冲数就会得到滑台补偿后的脉冲数,即建立几何域到控制域的映射关系。其中,该公式包含需标定求解的误差参数有2个像素值误差参数及5个误差角度参数。
(1)
2 标定参数的粒子群优化
线性标定[13]精度相对较低,各角度标定是顺序进行,各角度之间的计算具有关联性,当某一参数存在误差,后续用到该参数的另一参数即会受到该误差影响,产生误差传递与误差积累问题,影响标定结果。为了避免该问题的产生,提高各参数的全局适用性与可靠性,就要寻找一种方法对各误差角度参数进行统一求解,解决各角度推导的关联性造成的误差传递与积累问题,得到适用于整个装配区域的最优参数。
粒子群优化算法(PSO)是一种基于群体的智能进化算法,其中连续性粒子群算法是解决函数最优化问题的通用方法[16-18]。其采用信息共享机制,通过粒子的自我学习和向最佳个体学习的方法来实现对解空间的快速搜索。它适合在动态、多目标优化环境中寻优,与其他优化算法相比,PSO具有简单、求解速度快、调节参数少、易于实现等优点[19-21]。而该设备的误差补偿就是将某个模块的移动经过标定参数矩阵转换后控制另一模块到达相同位置的过程,位置偏差越小,转换精度越高,这本质上也是求标定参数最优解的过程。因此,本文选用改进的粒子群算法对各误差参数进行统一求解,进一步提高零件的装配精度。
如图4所示为PSO算法的流程图解。
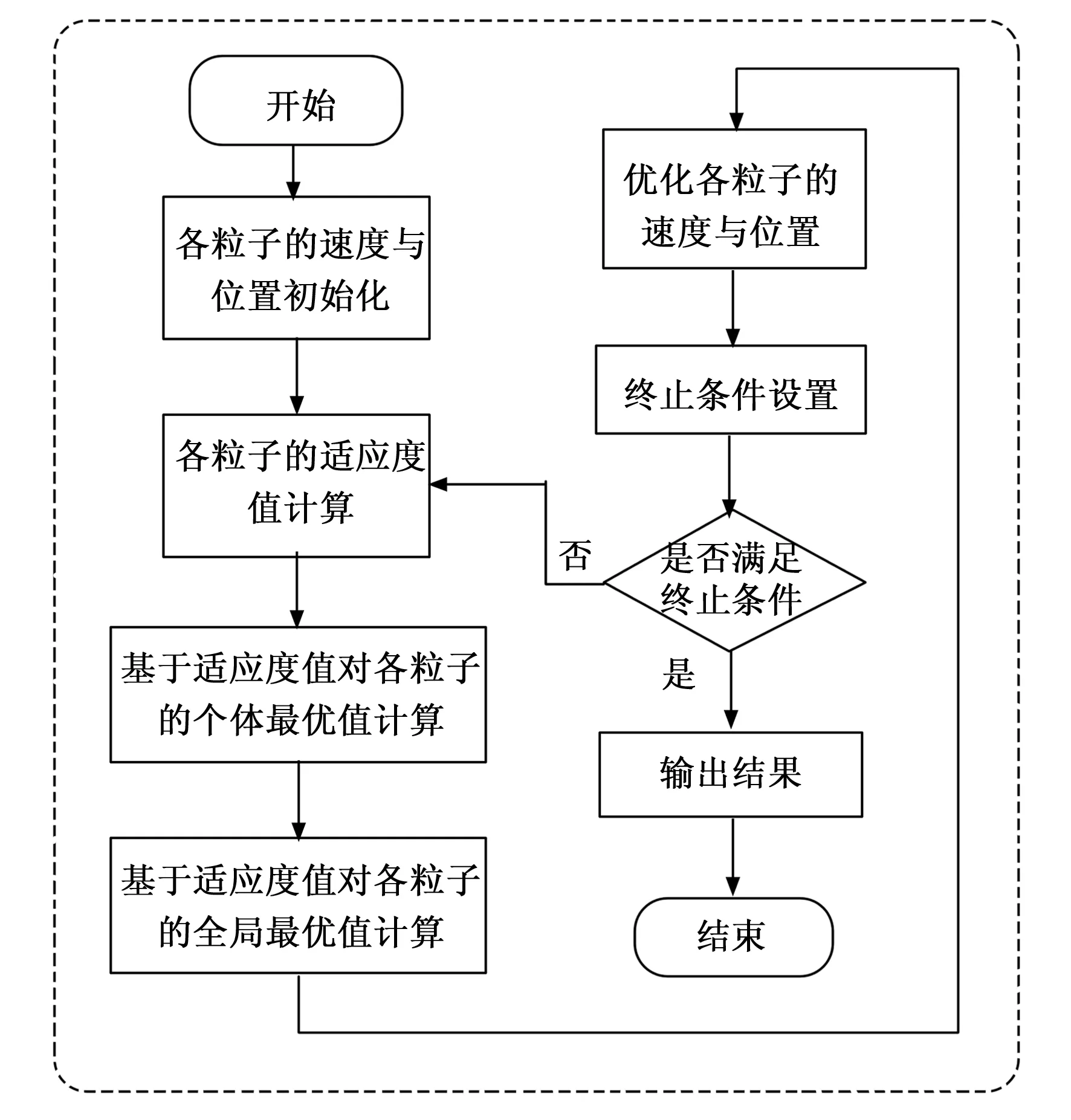
图4 粒子群算法流程图
以下为更新粒子的自身速度和位置的公式:
vij(t+1)=ωvij(t)+c1r1(pij(t)-xij(t))+
c2r2(g-xij(t))
(2)
xij(t+1)=xij(t)+vij(t+1)
(3)
其中:i表示粒子的个数,j表示粒子的维数;t表示迭代次数;r1和r2为随机数,一般在[0,1]中选取;ω表示惯性权重,可以设置为动态调整的,保证在迭代前期保证足够的全局搜索能力,迭代后期能够专注于局部最优解的搜索能力;c1和c2表示粒子群的学习因子,一般取值0~2;vij是粒子的速度,用户可根据自身情况设定;vij(t)是第t次迭代时,j维的粒子i的当前速度;pij(t)为个体目前最优值;g为整体粒子最优值;xij是粒子的位置;xij(t)是第t次迭代时,j维的粒子i的当前位置。式(2)由三部分组成:第一部分为“惯性”部分,反映了粒子的运动“习惯”,趋向维持自己先前速度;第二部分为“认知”部分,粒子根据自身搜寻的经历,趋向自身历史最佳位置;第三部分为“社会”部分,粒子间根据协同合作与知识共享的群体经历,趋向群体或邻域历史最佳位置。
基于以上粒子群算法,结合装配任务自身情况设计如下优化过程:
1)粒子设置。将第1.2节式(1)中的需要求解的7个误差参数设置为7维粒子。
2)特征点位与采点路径选取。装配区域如图5所示,为了更好的遍及整个区域,根据装配区域选取具有代表性的点位进行图像特征点采集,选择上、中、下三个平面上不与起始点相邻边的中点位置共10个点位作为标定点位。采集流程为用装配作业模块夹持零件,分别控制视觉模块和装配作业模块沿各自滑台方向运动相同的脉冲数,视觉模块搭载相机观测零件的同一特征点。为了便于自动化进行,选取空间任意一点,呈发射性方向向标定点位移动。记录下视觉模块滑台运动脉冲数[ΔXv0,ΔYv0,ΔZv0]T、图像坐标系下图像的坐标变化[ΔU,ΔV,0]T和装配模块滑台脉冲数[0,ΔYa0,ΔZa0]T(由于装配模块没有X向滑台,所以在进行X方向位移时只有视觉模块运动)。将其数据进行迭代优化得到最终的粒子。

图5 装配区域采集路径示意图
3)设置适应度函数。将优化迭代后的粒子代入到式(1)中,通过采集的数据进行求解装配模块的计算值[ΔX,ΔY,ΔZ]T,将其与实际值[ΔXa0,ΔYa0,ΔZa0]T相减,再分别计算XYZ三个方向的平方差,这三个方向的平方差相加即为一组误差,重复进行该过程直到得到10组数据,将适应度函数设置为其十组数据的和,如式(4)所示。
error =
∑110[(ΔX-ΔXa0)2+ (ΔY-ΔYa0)2+ (ΔZ-ΔZa0)2]
(4)
4)最优解求解。确定适合的种群数量、惯性权重、学习因子等,经过粒子群的不断迭代更新,选取式(4)中error的值最小时一组粒子所表示的数值作为最终的标定误差求解参数。
3 摆组件装配设备的标定实验与验证
本实验分别进行线性标定与粒子群优化的的标定实验计算采用不同方法得到误差参数。随后进行线性标定与粒子群优化的验证对比实验来验证标定精度。
3.1 标定对比实验
在进行误差角度线性标定时,基本思想是:通过观察标定板模块上的特征点,控制相应滑台进行运动,观察运动前后标定板上特征点在相机视野中的位置变化,最后将运动信息和坐标信息代入线性标定理论求解模型中计算,即可得到误差角。如图6所示为线性标定流程示意图。
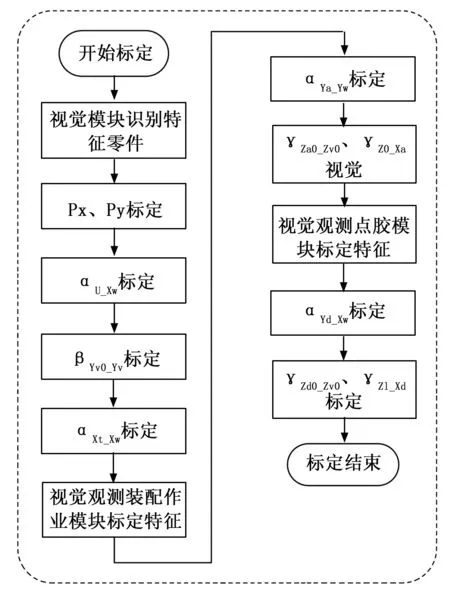
图6 线性标定流程示意图
粒子群算法优化选取式(1)中需要求解的7个参数作为实验粒子。选取3 000 μm×20 000 μm×12 000 μm的空间大小作为装配区域,按照如图5所示的滑台移动路径,进行10组数据的采集;确定粒子群算法本身的参数,根据误差参数本身的大小设置了各自的速度和位置范围,结合经验及对比实验得出:粒子数N取1 000;学习因子c1和c2取2;惯性权重ω取0.5;迭代次数t取100。将10组数据带入式(1)的统一补偿模型推导矩阵中。如图7所示为根据推导的标定模型设计的标定流程,根据该流程进行了标定实验,标定过程不借助外部安装的标定板结构,只采用设备现有的结构特征或零件特征。
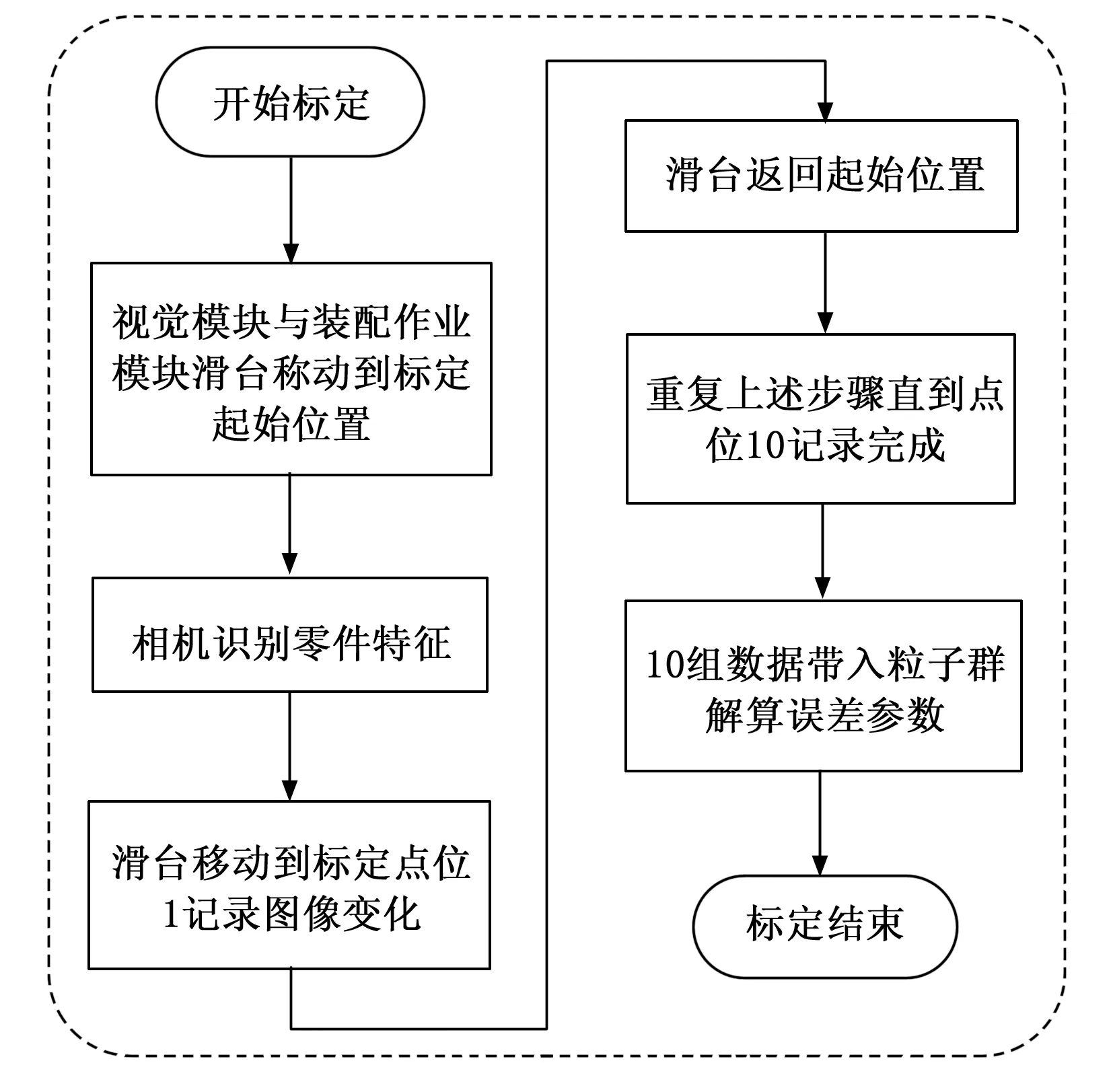
图7 粒子群优化标定流程示意图
使用Visual Studio软件基于.NET平台编写了自标定软件,开启软件后整个标定过程自动进行,整个标定流程在3 min 20 s内即可实现各误差角度参数的计算与结果输出,标定效率高效快速。考虑设备实际情况,受相机视野及滑台行程的影响,选定5 000 μm×25 000 μm×15 000 μm的装配区域的标定范围,该标定范围包含且大于装配区域。
为了比较线性标定与粒子群算法优化的标定结果,本文首先进行了线性标定的标定实验,其标定结果如表2所示,表3为粒子群优化计算后的标定结果。
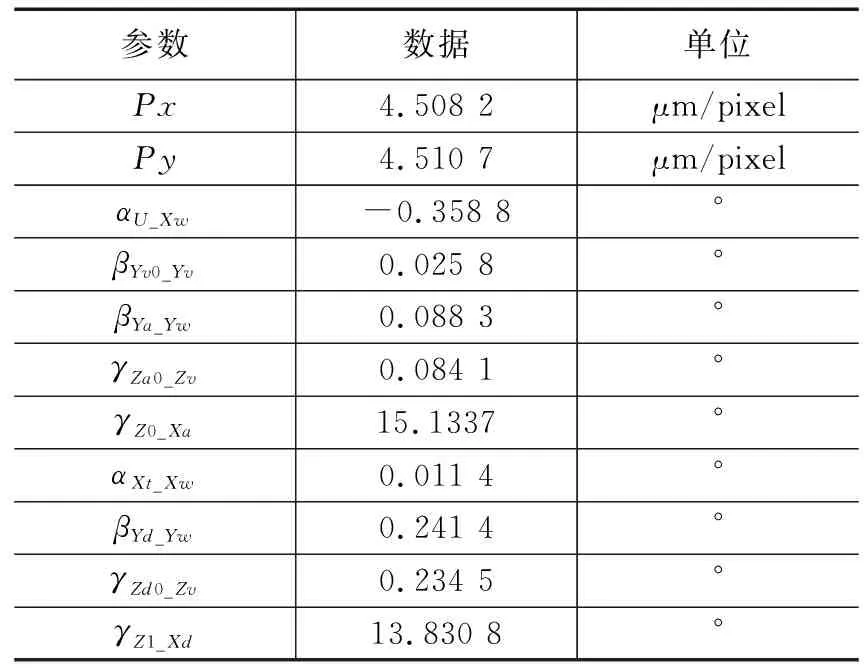
表2 线性标定结果
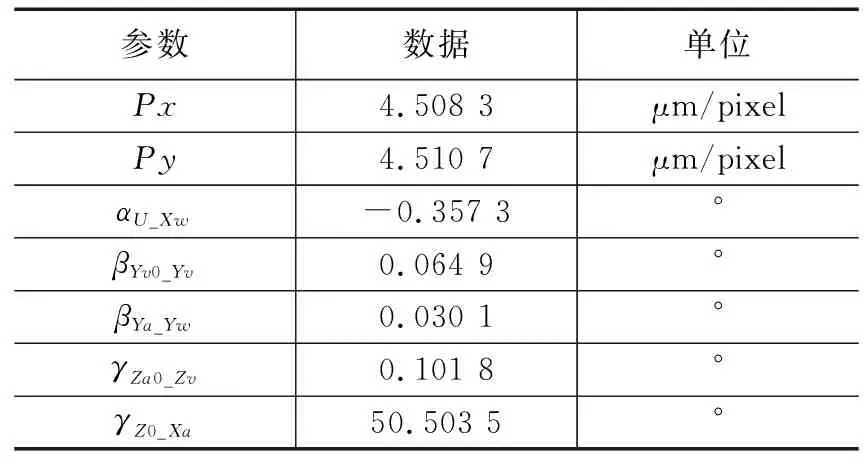
表3 粒子群优化结果
3.2 实验验证
在进行标定误差补偿的实验方法中,一般方法为:首先,滑台移动理论脉冲数,比较图像坐标系下特征点的图像坐标前后的像素差值;其次,将理论脉冲带入补偿模型中求解实际脉冲,比较其与理论脉冲的差值后将差值转化为图像坐标系下的像素差值,最后,比较两个差值,得到标定误差补偿结果。这种方法得到的结果不够直观,未能真正将补偿量添加到滑台移动中,只将理论脉冲数计算得到补偿值后与结果对比。
本文的误差补偿实验方法为将理论值带入补偿模型求解补偿的脉冲数后将其直接带入到滑台的运动中,最后只需对比图像坐标系下特征点的图像坐标前后差值即可。该方法将补偿的脉冲数带入到滑台的实际运动中,更符合装配任务的实际装配流程,通过滑台的实际移动直接输出结果进行比较,其结果更加直观,结论更具有说服力与可信度。
首先,选取装配空间中与粒子群训练时的采样路径不同的4条矢量位移[2 000,8 000,0]T、[2 000,0,6 000]T、[0,8 000,6 000]T、[2 000,8 000,6 000]T作为验证路径;其次,使用线性标定和粒子群算法优化的补偿误差,分别补偿到上述验证路径的各滑台移动中;最后,分别将补偿的上述路径带入到视觉模块和装配作业模块滑台脉冲中,并保持每次随机选取滑台的起始位置,重复运动该路径10次,记录下线性标定和粒子群迭代优化两种方法特征点在图像坐标系中的实际坐标变化(ΔUX,ΔVX)和(ΔUL,ΔVL)。使用式(5)和(6)分别计算线性标定和粒子群优化后的图像坐标与实际的偏差E1、E2。
(5)
(6)
图8为验证实验对比结果。

图8 粒子群优化前后验证数据对比
对线性标定和粒子群算法两种方法误差的均值和极大值进行计算,如表4所示。

表4 标定优化前后误差对比 μm
根据图8和表4得出结论,采用线性标定的方法求解的误差参数,在实际操作空间会产生较大误差,但是经过粒子群算法优化后的标定模型,能够显著降低相关误差造成的影响,并且标定出的参数对于装配空间而言体现出更强的适应性。通过实验能够得出结论,优化后的标定补偿结果优于线性标定,其验证结果能够将误差控制在5 μm以内,很好地满足了标定精度的要求。
4 结束语
本文针对摆组件装配设备提出一种通用自标定方法。该方法不借助标定板,仅通过识别设备固有特征进行标定,再结合粒子群优化完成误差参数的统一求解,最后根据推导的误差补偿模型实现误差补偿,实现几何域到控制域的映射。实验结果表明,粒子群算法优化后的标定参数达到的标定验证精度在5 μm以内,有效解决误差积累与传递问题,满足了摆组件装配精度要求。同时,该方法不借助标定板,可在同类型微装配设备工作中微调后使用;自动化程度高,操作性好,标定时只需要运行软件即可实现自动操作流程;标定实验验证方式更加直观。该标定方法可广泛应用于微装配设备的标定,为微装配设备提供了一种简单有效的标定方案。
