基于IWOA算法求解并联冷机负荷分配问题

于军琪，康智桓，荆 竞，赵安军，陈时羽

(1.西安建筑科技大学，西安 710055；2.中国建筑西北设计研究院有限公司，西安 710018)

0 引言

近年来在中国，建筑消耗了大约20%的一次能源。城市建筑可以消耗高达70%的城市一次能源[1]。所以提高建筑能源效率对于可持续发展至关重要。冷水机组通常服务于商业建筑。作为中央空调系统的主要部件，冷水机组约占商业建筑制冷能耗的35%。由于冷水机组能耗巨大，因此，如何在不同冷负荷下运行制冷机系统，使能耗最小化成为一个重要的问题[2]。通过仔细设计和运行冷水机组，发现多台冷水机组系统由不同性能特性和容量的冷水机组成，因此各冷水机的最优负荷比组合成为一个有价值的研究课题。

近年来，冷水机组负荷优化分配(OCL，optimal chiller load)问题受到越来越多的关注，研究人员使用各种优化算法不断对优化结果进行改进。文献[3]在最优冷水机组负荷研究中采用拉格朗日法(LM，Lagrange method，)最小化不同冷负荷下的能耗，结果表明拉格朗日法能使能耗最小化，但在低需求时不能收敛；紧接着文献[4]提出利用遗传算法求解，遗传算法克服了低需求下的收敛性，但相比于拉格朗日法平均能耗提高了0.4%左右；文献[5-6]又提出利用模拟退火法(SA，simulated annealing)和梯度法(GM，gradient method)改进拉格朗日法的收敛性，发现该方法能在短时间内产生精度较高的结果。文献[7]采用粒子群算法(PSO，particle swarm optimization)对问题进行求解，发现PSO相比于GA算法能够获得更好的优化结果。因为OCL问题的变量是连续的，所以文献[8]采用连续遗传算法(CGA，continuous genetic algorithm)和粒子群算法来解决，而研究也表明粒子群算法能够改善遗传算法和拉格朗日法的性能。文献[9]提出了一种差分进化算法，该算法在寻优方面优于遗传算法，并克服了遗传算法存在的问题。文献[10]提出了一种基于高斯分布函数的改进萤火虫算法(FA，firefly algorithm)，优化了多冷却器负载问题中的能耗。文献[11]提出了一种新的差分布谷鸟搜索算法(DCSA，differential cuckoo search approach)，该算法基于差分算子，提高了算法的整体寻优能力。文献[12]使用非线性波纹权重因子和自适应排斥因子的改进波纹蜜蜂群优化算法(IRBSO，improved ripple bee swarm algorithm)算法，并将其用于解决冷水机组的经济调度问题。文献[13-4]提出的改进人工鱼群算法(IAFSA，improved artificial fish swarm algorithm)和改进入侵杂草算法(EIWO，improved invasive weed optimization)也为解决此问题提供了更好的解决方案。文献[15]提出运用改进分数阶达尔文粒子群算法(IFODPSO，improved fractional order Darwinian particle swarm optimization)求解，也是解决OCL问题的有力工具。结果表明，与现有优化算法相比，该算法在收敛精度、收敛速度和稳定性等方面的综合性能有了显著提高。以上研究表明，元启发式算法和数学规划方法都是解决OCL问题强有力的工具且均能从中央空调系统实际用能情况出发解决问题。但是元启发式算法需要较大种群规模、对种群初始化要求较高等问题使得一种优化算法在特定优化问题上的优化性能较好，但是并不能推广到大多数优化问题上从而算法适用性大打折扣。鲸鱼优化算法[16](WOA，whale optimization algorithm)是2016年提出的一种基于鲸鱼捕食习惯而研究出的一种新的智能算法，本文以该算法为基础解决冷水机组负荷优化分配问题。

WOA算法的推广引起了研究者们的关注，并在文献[17-18]中用于求解单目标热电厂经济调度问题。基本的WOA为中小型测试系统提供了更高质量的解决方案，并且收敛速度更快。但是，对于大规模复杂问题，基本WOA算法由于早熟收敛、收敛速度慢等问题往往不能收敛到最优解。这是因为在基本的WOA算法中，局部勘探和全局开发之间存在差异。针对基本WOA出现的问题，许多研究者都做了不同的修改，通过适当平衡勘探阶段和开发阶段来提高WOA性能。文献[19]引入了改进的混沌鲸优化算法(CWOA，chaos whale optimization algorithm)来求解太阳能光伏电池的参数估计，该方法利用混沌映射进行计算，并自动选择方法内部参数。文献[20]引入了一种带局部搜索策略的混合鲸鱼优化方法来求解置换流水车间调度问题。文献[21]采用了一种基于最新开发的WOA的新的MLP训练方法来优化神经网络中的连接权值。文献[22]为了准确提取不同太阳能光伏模型问题的参数，提出了一种改进的鲸鱼优化算法。该方法采用了两种猎物搜索策略，有效的保持了勘探与利用的平衡，提高了WOA算法的性能。从以上研究可以看出，不同学者对于基本鲸群算法出现的收敛速度慢、寻优精度低、早熟收敛等问题提出的各种改进鲸群算法应用于各领域的优化问题均获得了良好的实验结果。

综上所述，由于OCL问题优化变量的维度及最终结果由冷机的数量及各冷机的性能参数决定，基本鲸群算法已经无法满足针对OCL问题中出现的高维问题，快速收敛到全局最优解。因此，提出一种改进鲸群算法(IWOA，Improved whale optimization algorithm)，并通过仿真实验对其性能进行检验。

1 问题描述

冷水机组由于运行灵活、备用容量大、检修中断少等特点，常采用并联的多套冷水机组与共用配电系统相连接[23]。图1展示了一个典型的解耦冷冻水系统。冷冻水系统的多台泵通过旁通管连接，旁通管连接回水总管和供水总管。冷水机组与泵机组一体化，相互独立运行[24]。考虑到需求增量的发生，需要比冷水泵提供的流量更大的流量。总管由回流水通过旁路提供，旁路定义了额外冷水机组容量的要求。因此，将启动另一台冷水机泵。相反方向的水流决定了产能过剩的条件，这就关闭了冷水泵。在全电制冷的多台冷水机组系统中，在满足负荷需求的情况下，各机组能耗之和最小时，机组性能最佳。PLR (partial load ratio)定义为冷水机的冷负荷与冷水机功耗的比值。

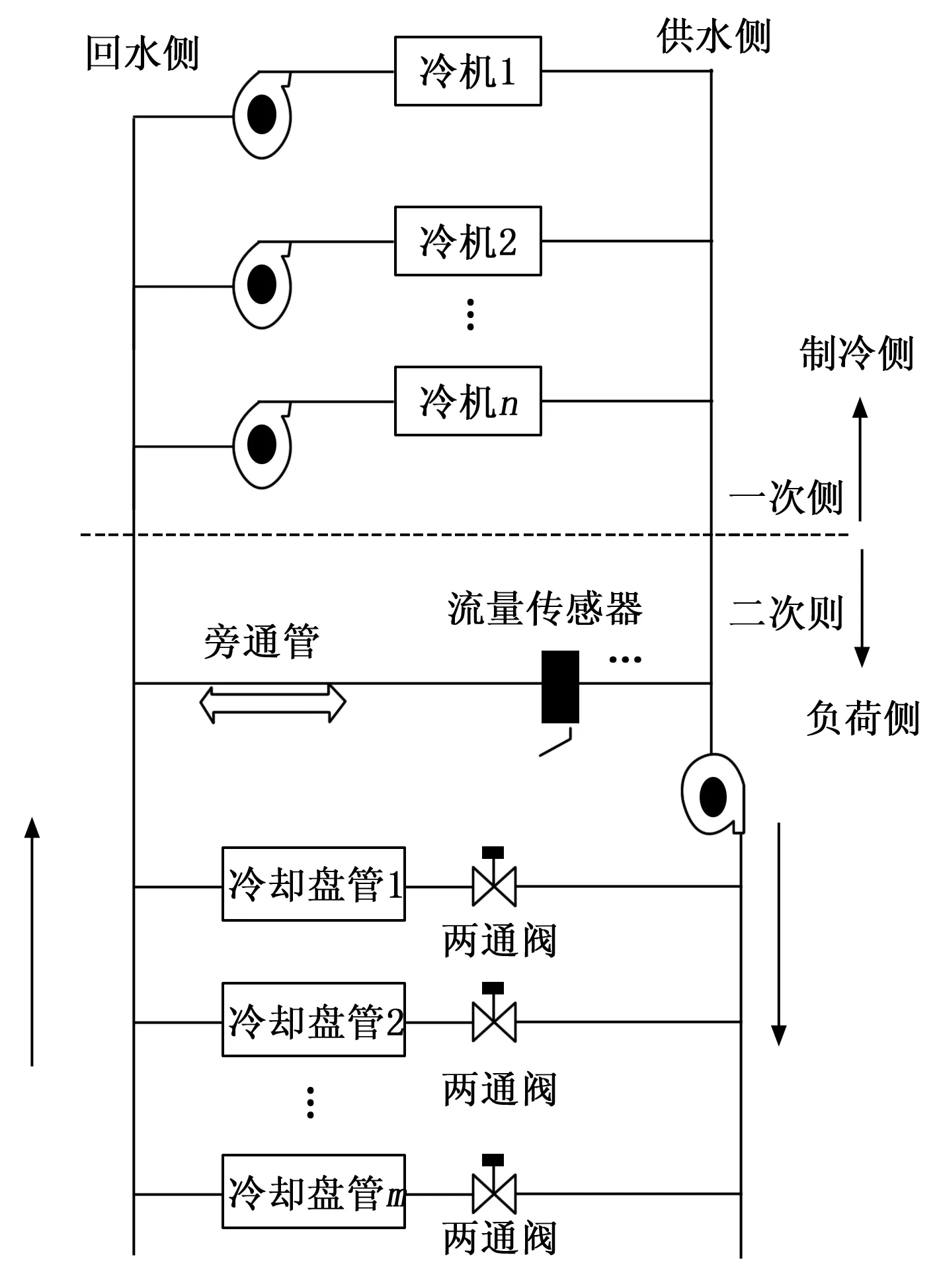
图1 多冷机系统结构图

每台冷机的性能参数都有所不同，冷机负荷的变化取决于末端负荷需求的变化。为了将系统冷负荷分配给制冷机组，多冷机系统允许可变的水流通过冷却盘管，并保持恒定的水流通过冷却器。此外，允许供水和回水通过旁通管道彼此流动，并且可以根据系统冷负荷需求来控制水流。

典型OCL问题的优化目标，是使多台冷水机组系统的总功耗最小化。因此，它主要是指在能满足整个系统末端负荷需求情况前提下，追求达到一种至少不应超过整个系统的运行功率极限条件下的系统最大的冷机部分负荷比PLR使末端冷机部分的负荷功率总和达到最小，从而获得最佳的系统性能，实现节能减排的目的[15]。因此本文将离心式冷水机组的功耗描述为：

(1)

式中，Pi为第i台冷水机组功率，ai、bi、ci、di为第i台冷机本身的功耗系数，Ri为第i台冷机的部分负荷比。

OCL问题是指在满足给定的目标函数最小的情况下，求一个不大于中央空调系统最低运行功率限制条件下的冷水机组部分负荷率PLR值，使之能在满足整个中央空调系统末端负荷要求条件的情况条件下仍以系统最低限度的最低运行总功率来工作，考虑到系统的冷负荷平衡，目标函数如(2)式所示应最小化：

(2)

式中，OF为并联冷机系统总功率，m为并联冷机台数，根据制造厂商的建议，当冷却器打开时，PLR值必须大于0.3。当冷却器关闭时，PLR值为0 。解决OCL问题的目的是找到冷水机组PLR的最佳值，该值可以获得最小的运行功率并满足运行约束。

因此，并联冷机负荷分配优化模型的目标函数和约束条件的数学式如下：

min(P)

(3)

s.t.0.3≤Ri≤1或Ri=0

(4)

(5)

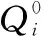
2 鲸群优化算法

2.1 标准鲸群优化算法

标准鲸群优化算法(WOA，whale optimization algorithm)包括几个步骤：

2.1.1 包围猎物

WOA算法将目前群体的最佳结果作为精英鲸鱼的位置，其余个体将精英鲸鱼的位置作为猎物的位置。通过改变位置进而包围猎物，鲸群的行为公式如下：

(6)

(7)

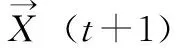
(8)

(9)

(10)

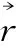
2.1.2 气泡网方式狩猎

气泡网觅食法是座头鲸独特的捕猎方式，为了对座头鲸独特的捕猎方式进行数学建模，设计了以下两种方法。

1)收缩包围机制：

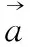
图2 鲸群算法收缩包围策略示意图

2)螺旋包围机制：

螺旋包围机制中，通过计算座头鲸与猎物之间的距离建立座头鲸与猎物之间的螺旋方程。螺旋方程如下：

(11)

(12)

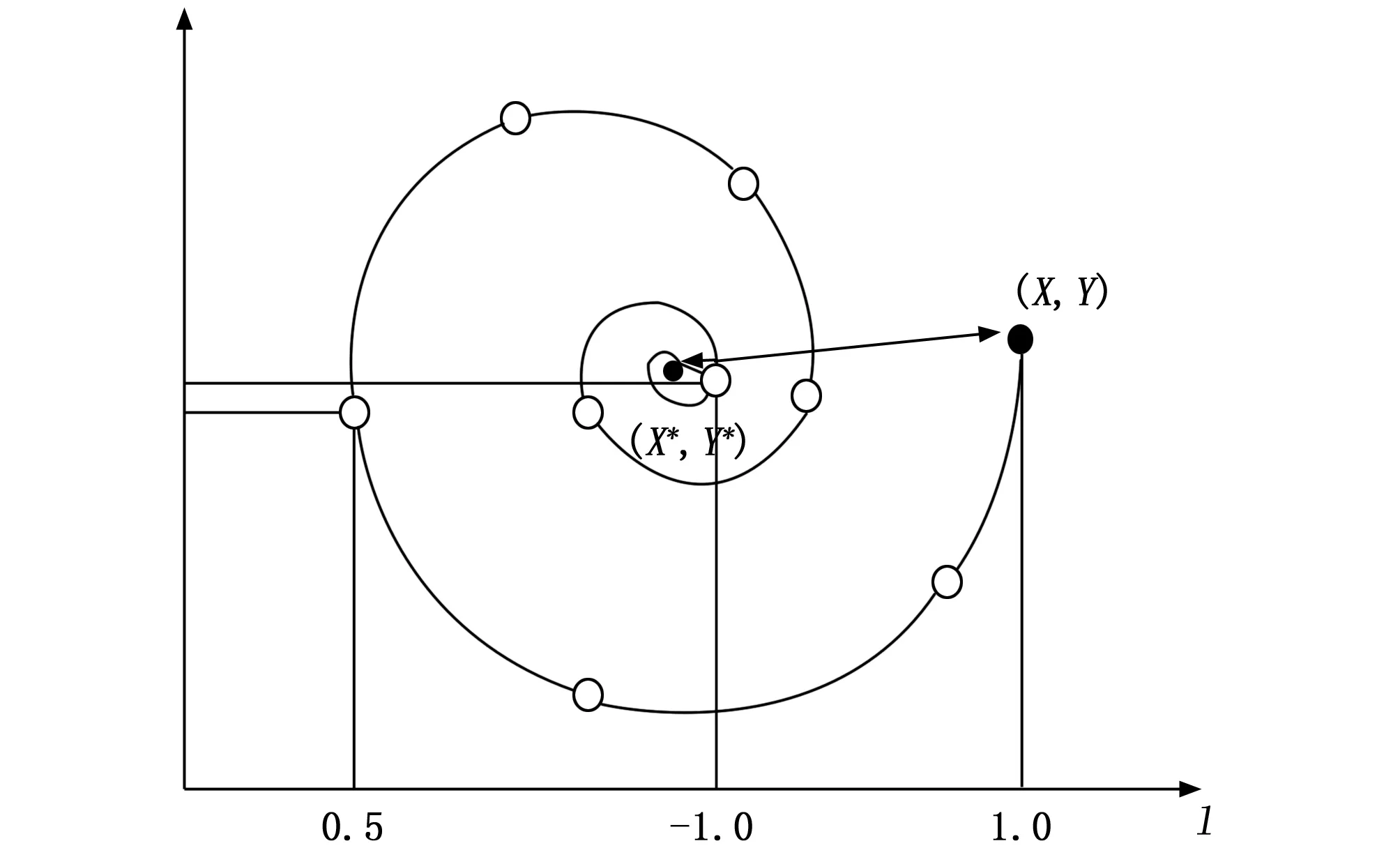
图3 鲸群算法螺旋包围策略示意图

当座头鲸群不断朝猎物周围方位移动觅食时，首先会绕着一个逐渐缩小的圆环包围猎物，与此同时不断螺旋上升对猎物进行捕食，为了模拟这种捕捉方式，假设有百分之五十的可能性在收缩包围机制或螺旋包围机制中选择并更新座头鲸的位置。数学模型如下：

(13)

其中：p为[0，1]之间的随机数。

2.1.3 搜索猎物

在捕猎过程中，鲸群会参照其他族群的位置来改变自己的当前位置，以这种方式扩大搜索范围进而搜寻更优的猎物位置。WOA算法中，每个个体根据收敛因子|A|的改变确定下一步的搜索范围。当|A|>1时，个体鲸鱼将扩大随机捕食的搜索范围，并执行全局搜索。数学模型如下。

(14)

(15)

综上所述，鲸群算法的综合搜索策略如下所示：

(16)

2.2 改进鲸群优化算法

2.2.1 混沌映射初始化种群

鲸鱼的初始位置是随机生成的，通常情况下初始值会随机遍布整个解空间。针对不同的优化问题，初始值对算法的收敛精度和速度有不同程度的影响[24]，基本鲸群算法在解决函数优化的问题时，往往使用了随机初始化种群的方式，而无法确保初始参数在解空间内均匀分布，这就导致当初始值远离了全局最优解，就会大大增加搜索时间，延缓算法收敛速度，同时也有陷入局部最优解的可能性。

混沌运动因为其遍历性、随机性和规律性等特点，能够使初始化后的种群更均匀地在整个解空间分布。目前，它已被广泛应用于蜂群、灰狼和粒子群优化等智能算法中。本文首先引入了Skew tent混沌映射，Skew tent混沌映射在其参数区域内是一种混沌映射，同时拥有均匀的分布函数以及良好的相似性。与更广泛使用的logistic映射相比，它减少了解空间边缘区域的高分布率问题，并且具有良好的均匀分布性能。Skew tent算法公式为：

(17)

其中：φ∈[0，1]。当φ=0.5时是tent映射最经典的形态。此时，得到的序列是均匀分布的，并且针对各个参数有着几乎相同的分布密度[25]。所以本文引用的tent混沌映射如下所示：

(18)

2.2.2 收敛因子改进

(19)

其中：t表示当前迭代次数，Tmax为最大迭代次数，μ取2，1，0.5。

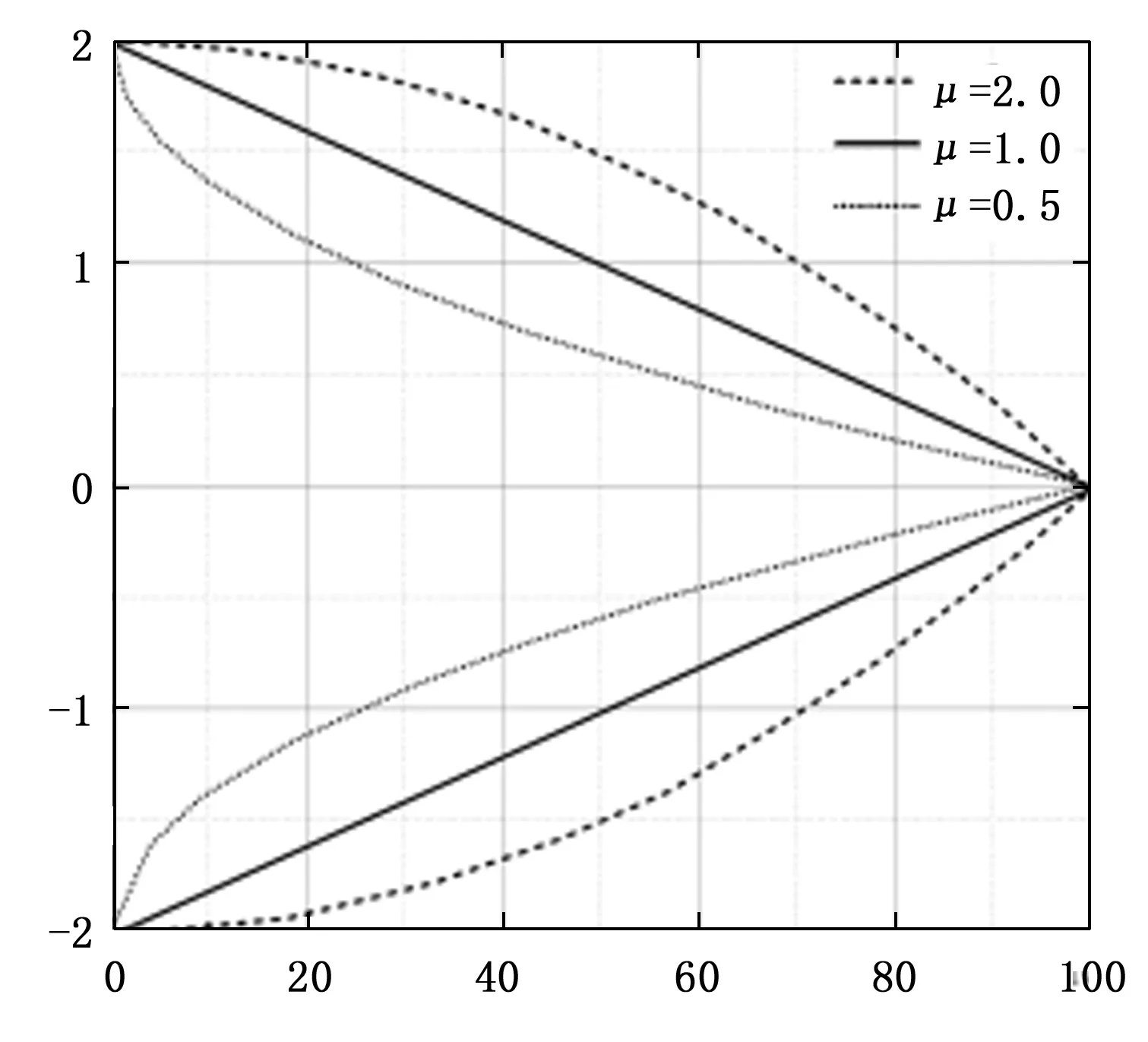
图4 变异指数迭代变化图

2.2.3 改进螺旋更新位置

从式(11)中我们能够看到，WOA算法的螺旋更新策略模型可以帮助种群在后期阶段快速地聚集。虽然它能够提高算法后期的收敛速度，但同时也会损失种群的多样性，从而増大算法陷入局部最优解的风险[26]。因此，本文对螺旋位置更新模型做出如下改进：

(20)

(21)

综上所述，改进鲸群算法流程图如图5所示。

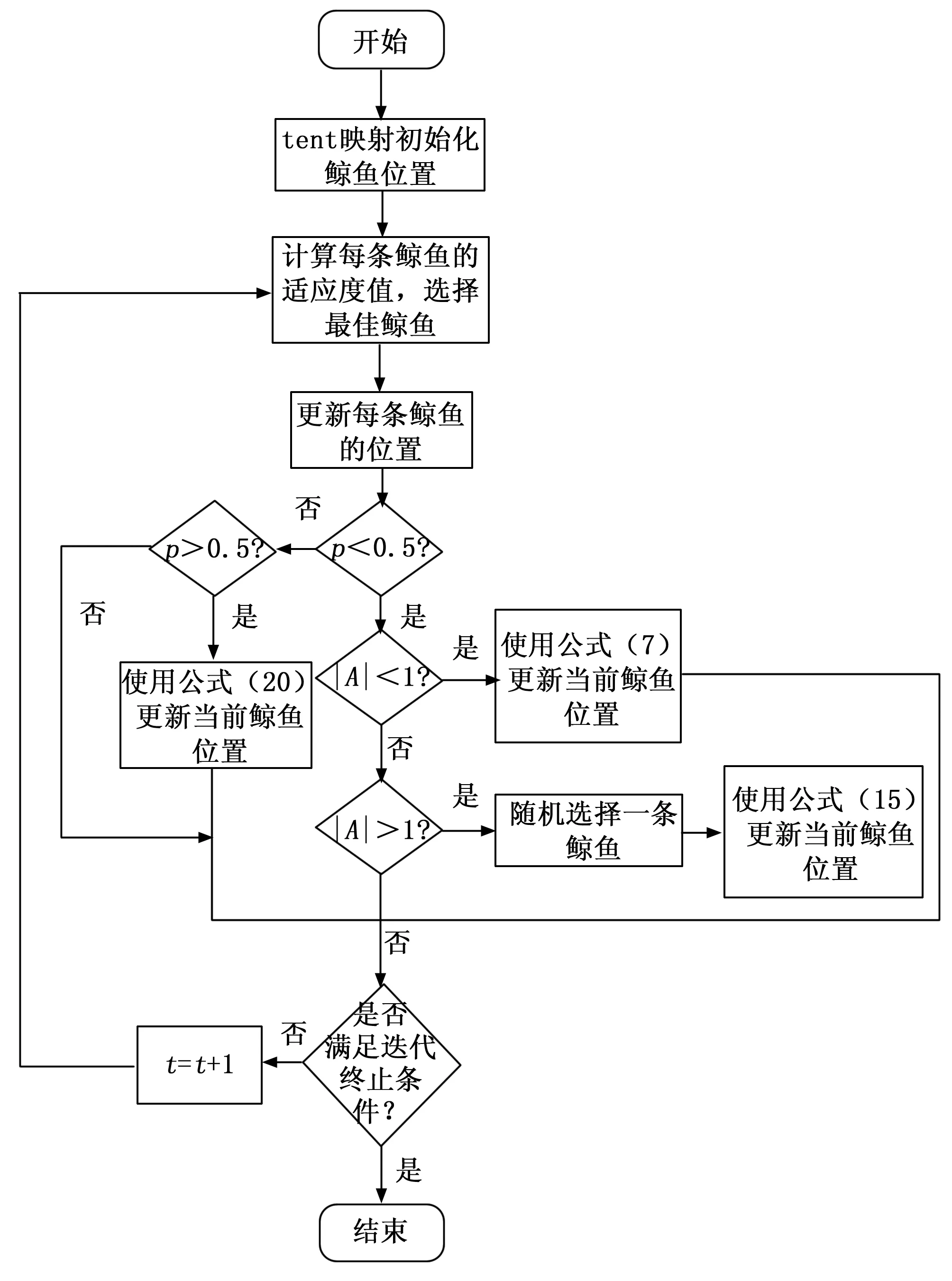
图5 改进鲸群算法流程图

3 测试案例与结果分析

3.1 测试案例

为了证明IWOA算法在解决OCL问题上的优势，选择了两个典型的并联冷机系统验证算法性能。在这项研究中，为了说明IWOA算法解决OCL问题的最佳能力，对两个案例进行了测试。第一个多冷水机组系统由3个800 RT机组组成。第二个多冷水机组系统由4个1 280 RT机组和两个1 250 RT机组组成。两组冷机工况数据均选取来自台湾新竹科技园内的一家半导体厂的冷机数据进行实验。表1展示了两个案例冷机的性能参数。

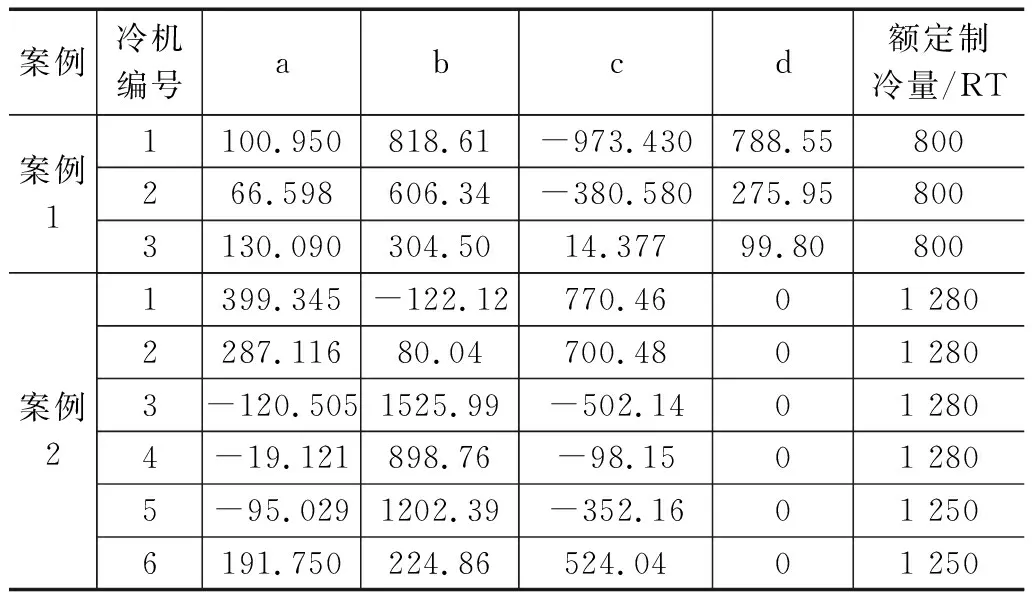
表1 测试案例冷机性能参数

3.2 结果分析

为消除偶然性，本研究所有实验数据均在对每个实验工况分别进行了30次独立实验基础上得到的，首先将改进鲸群算法用于OCL问题的求解。在案例1实验中将IWOA算法与GA[4]、PSO[7]、IFODPSO[15]等其他曾用于求解OCL问题的元启发式算法进行对比，结果如表2所示。从表2可看出IWOA算法在各工况下运行的结果均优于GA算法，在不同负荷需求下可节能2.84～149.93 kW不等，特别是当负荷需求低于1 440 RT(60%)时，均节能超过100 kW。当冷机在高负荷需求条件下运行时，节能效率有所下降，但依然可节能2.84～7.16 kW。与PSO、IFODPSO相比在各种负荷条件下均获得了相似的优化结果。在案例2的实验中，将IWOA算法与GA、PSO、DS算法进行了对比，如表3所示：表3显示了冷水机组的总功耗和每台冷水机组的部分负荷比，IWOA算法在不同需求下与GA、PSO、IFODPSO算法相比可节能0.95～159.79 kW。当部分负荷比小于80%时，IWOA算法计算的最小能耗比GA算法高1～4.3%，比PSO算法高1.6～2.1%，比IFODPSO算法高1.59～2.19%。在部分负荷比高于80%时，IWOA算法的优化结果与IFODPSO算法相同。与其他优化算法相比在统计平均运行时间方面，IWOA算法优于PSO算法和GA算法。这是因为提高算法收敛精度和减少运行时间是两个相互矛盾的目标，但随着计算工具性能的不断提高，这一矛盾得到了很好的解决[25]。图6展示了两个不同案例下IWOA算法的收敛曲线，对于案例1对应的三台冷机低维问题，IWOA算法可以保证在10代之内快速收敛到最优值，这是因为通过混沌映射，将初始化粒子均匀遍布解空间，以及通过变异指数对收敛因子的改进，既可以加快算法的收敛速度又可以保证算法不易陷入局部最优解。而面对案例2的6台冷机对应的高维问题，算法相应的收敛速度有所减慢，但在30代内算法就能保证收敛到最优值，通过实验可以看出算法具有良好的收敛性。从表4可以看出，将案例1和案例2中的WOA算法与IWOA算法在每个负荷需求下30次独立运行后的最大、最小和平均能耗进行了比较，并通过标准差验证了能耗的离散程度，以此来验证算法的稳定性。案例1中，当符合需求低于60%时，IWOA算法标准差为0，说明了在低负荷条件下，IWOA算法运行非常稳定。当符合需求高于60%时，两种算法的标准差均维持在较低水平。说明两种算法在针对只有3台冷机的低维优化问题时，均展现出了算法的稳定性，而IWOA算法相比于WOA算法稳定性更佳。案例2中，当负荷需求低于75%时，IWOA算法非常稳定，标准差为0，并在高负荷需求下，标准差维持在0.004 3～0.007 3这一低水平下。而WOA算法在案例2中的标准差差距较大分别达到了28.358 7、0.979 4、2.369 1、6.833 6、9.468 7远远高于相同工况下IWOA算法所得结果标准差。由此可见WOA算法在面对6台冷机对应的高维优化问题时，容易陷入局部最优解，使得数据差异明显，从而导致标准差差距较大。此外，2个案例中IWOA算法相比于WOA算法在不同负荷需求条件下总功率的最小值、最大值、平均值等都要更低，更加证明了IWOA算法的优势。

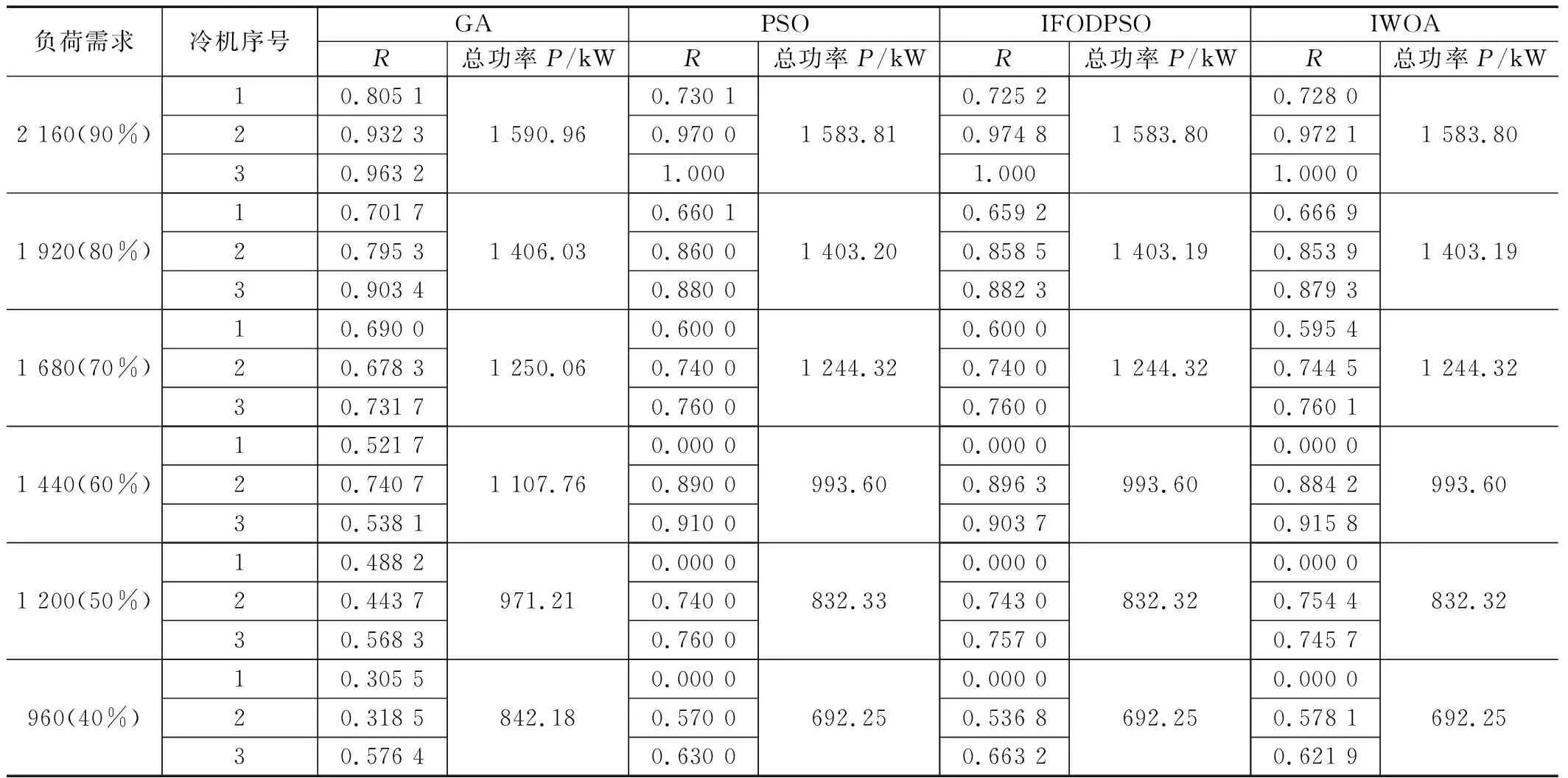
表2 案例1中GA、PSO、IFODPSO、IWOA算法结果对比

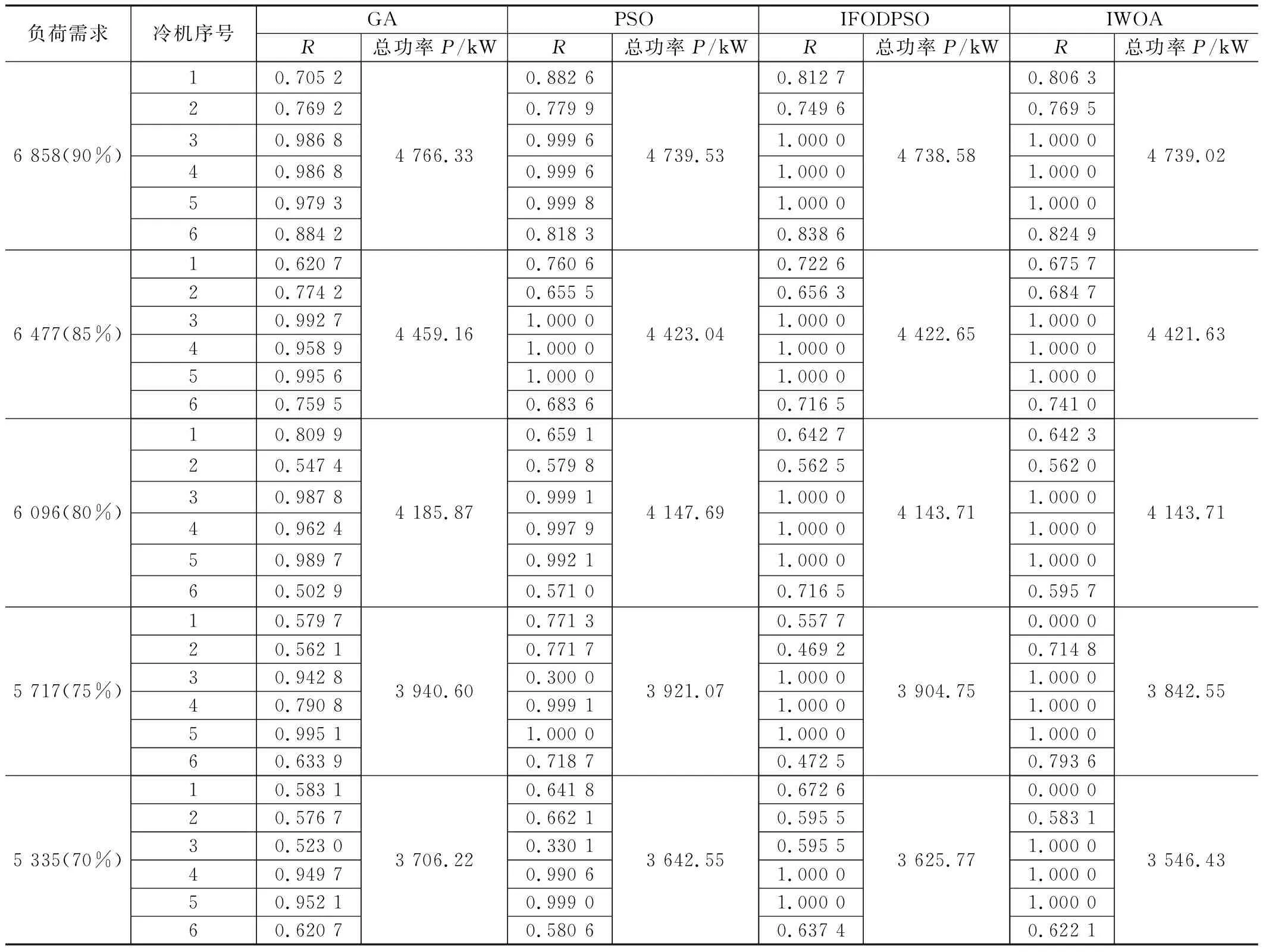
表3 案例2中GA、PSO、IFODPSO、IWOA算法结果对比

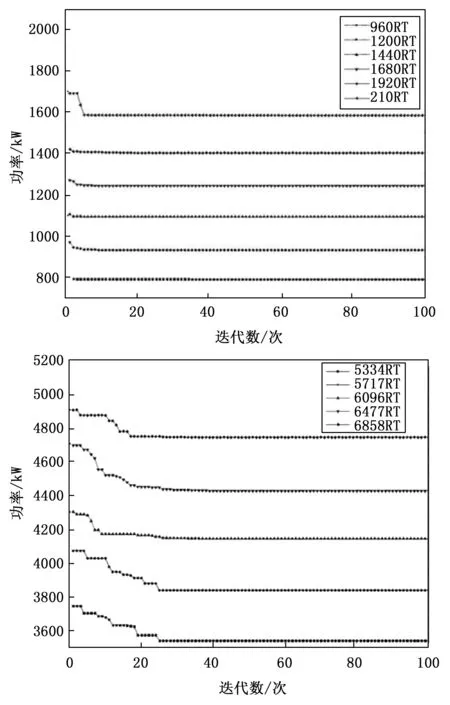
图6 不同情况下IWOA算法收敛曲线

另外图7显示了WOA算法和IWOA算法在两个案例中30次独立实验的平均计算结果与最优预测值的相对误差。

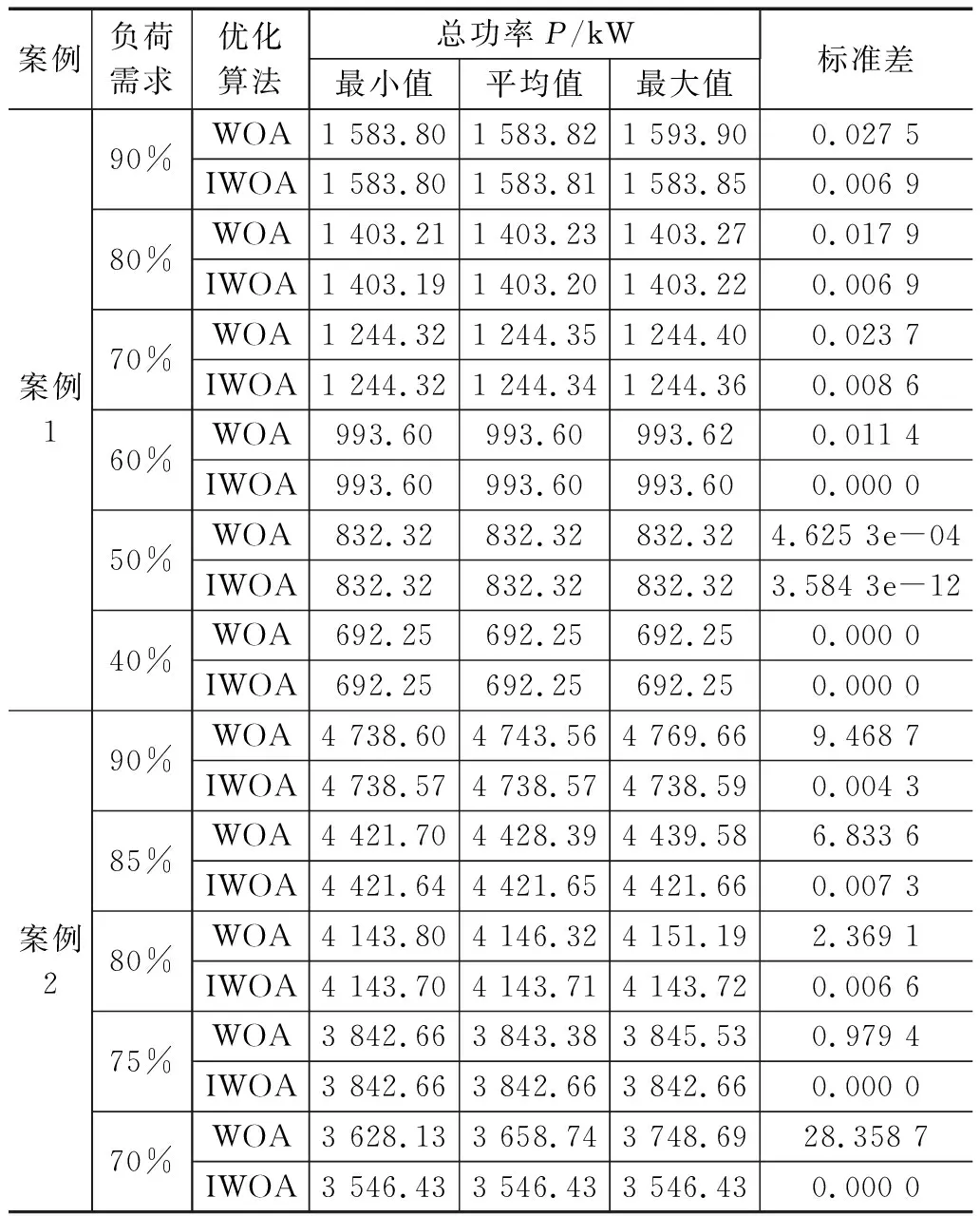
表4 WOA算法与IWOA算法优化结果对比

首先针对图(a)和图(c)分别对应的案例1的运行结果可看出，WOA算法相对误差均低于0.015%，负荷要求为40%和50%时，算法曲线平坦，负荷要求为80%和90%时相对误差出现了一定的震荡。而IWOA算法在负荷需求为40%、50%、60%时曲线均比较平坦，没有出现明显的误差。负荷需求为70%、80%、90%时最大相对误差也不超过0.003 5%。针对图(b)和图(d)分别对应的案例2的运行结果，WOA算法的相对误差均低于5%，负荷需求为70%和75%时曲线较平坦。IWOA算法相对误差均低于0.000 6%，负荷需求为70%和75%时曲线较平坦。图中IWOA算法在30次独立运行的实验结果相对误差虽然在某些工况下有所变动，但相比于WOA算法误差更小、曲线更加平坦从而验证了算法可靠的稳定性。

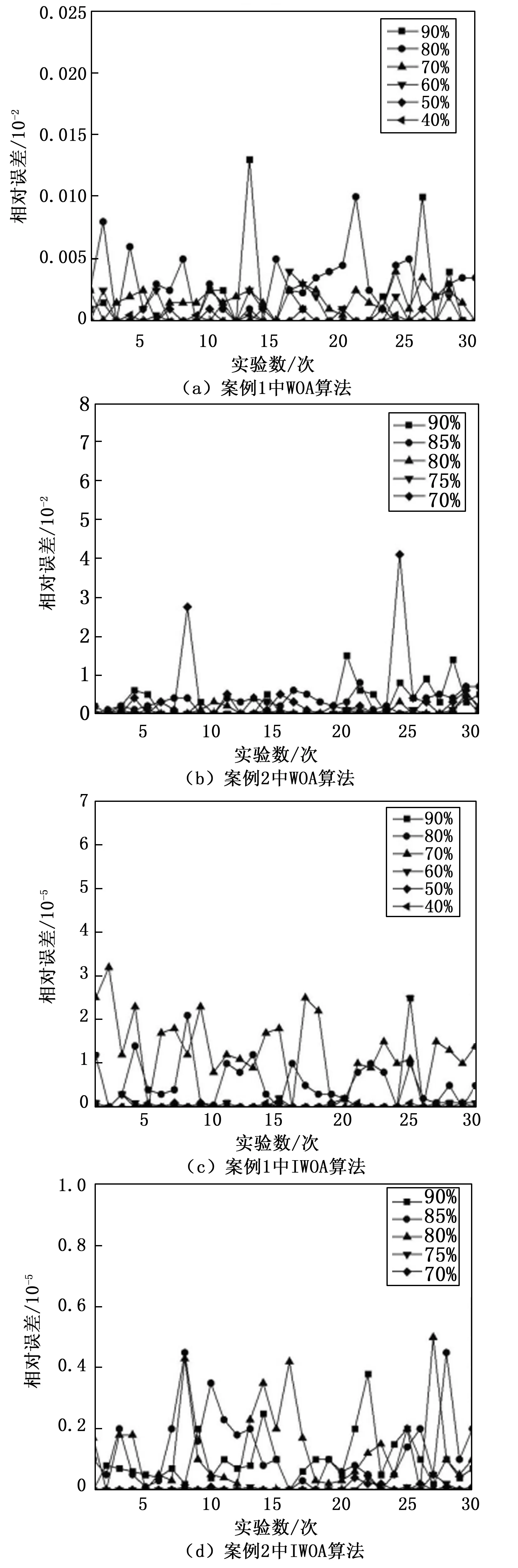
图7 不同案例下WOA算法和IWOA算法相对误差

通过实验表明，IWOA算法是解决OCL问题的一种行之有效的方法。

4 结束语

通过增加冷却需求和冷却器数量，每个机组必须以最高效率运行，并应将功耗降至最低。因此，为了降低建筑物或公司的运营成本，减少污染物的排放，OCL问题变得越来越重要。在这项研究工作中，IWOA算法作为一种有效的优化方法被引入到OCL问题中。本文中用于解决两个不同的测试系统，以评估该方法的有效性和性能。将所提供的最优解与其他优化方法进行了比较，结果表明，这些优化方法在功耗方面有了显著的提高。IWOA算法的收敛特性表明它能够在较短的时间间隔内获得最优解。该方法可方便地推广应用于大型多冷水机组系统的OCL问题。未来的趋势可以集中在研究大规模系统中的OCL问题和冷水机组的每日优化调度上。此外，制冷机满足制冷需求过程中的废热可以回收利用，以满足系统的热需求。