无人机天钩回收纵向控制系统设计与实现
2023-08-03张剑锋王朋飞
张剑锋,王朋飞
(西北工业大学 365研究所,西安 710065)
0 引言
天钩回收型无人机摆脱了传统滑跑型无人机对跑道的依赖,大大增强了部署和使用的灵活性。同时由于不必安装回收降落伞,减少了无人机死重,提高了其任务装载能力,并且降低了无人机由降落伞包导致的系统复杂度与使用维护难度。正是这些突出的优势,使得天钩回收无人机成为一个研究和设计的热点方向。然而相较于滑跑型与伞降型无人机,天钩回收对无人机的高度、速度、航迹控制精度提出了更高的要求。撞绳点的纵向位置和撞绳速度会直接影响机翼承受的过载大小,在撞绳回收过程高度控制精度一般要求小于1米,飞行速度则要稳定地保持在略高于安全速度的一个较小的许用速度区间内。
目前很多无人机纵向控制的常规方案是假设高度通道与速度通道相互独立,按照两个独立回路分别控制飞行高度和飞行速度[1],然而高度与速度实际上是存在相互耦合影响的。在要求飞行高度与飞行速度同时准确控制的无人机撞绳回收场景中,这种控制方式难以使两者同时达到预期的控制精度,从而容易造成一次撞绳成功率低,回收损伤风险较大的问题。也有文献采用了LADRC线性自抗扰等控制方法进行定高控制[2],仿真效果较好,但未见工程化实现与真实飞行数据的验证。此外,目前的控制系统一般均基于理想的飞行参数或者高精度的传感器数据,而对于天钩回收无人机来说,其重量都不大,也不具备装载高精度传感器的舱内空间,因此如何基于精度不高的小型传感器实现高精度天钩回收控制也是一个挑战。
针对上述问题,本文设计一种在配置低成本传感器的条件下利用油门和升降舵实现高度和速度通道协调控制的方法,并通过附加姿态约束使得无人机在天钩回收时的速度、高度与俯仰角均在最佳范围内。这种方式能够大幅提高一次撞绳成功率,实现高精度的撞绳点控制以及速度与姿态控制,既避免了因控制精度低导致频繁复飞带来的风险,也避免了撞绳时由于撞击点不够精确或速度过大导致的机翼损伤或使用寿命下降。同时,该控制方法易于工程实现,可直接部署到飞控计算机应用于实际的飞行试验。
1 控制系统组成与原理
控制系统组成框图如图1所示。无人机为控制对象,该控制系统包括的部件有:微航姿系统、差分卫星信号接收机、飞控计算机、升降舵机与油门舵机。
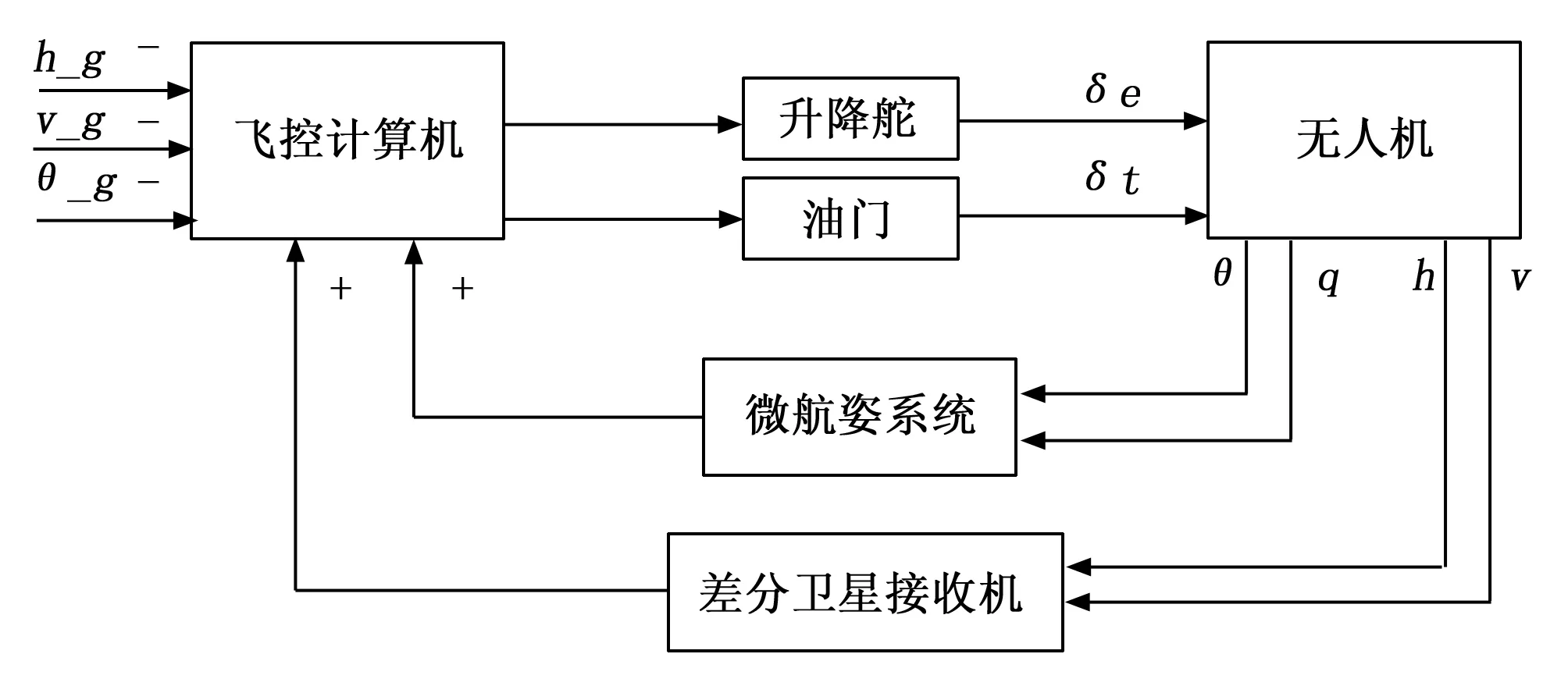
图1 天钩回收纵向控制系统组成框图
微航姿系统用于测量无人机的俯仰角、滚转角、航向角以及3个方向的角速度;差分卫星信号接收机用于获取无人机的高度、地速和位置信息;升降舵机、油门舵机分别用于执行相应的伺服运动指令,进而控制无人机的升降舵面与油门;飞控计算机用于采集各个传感器的测量数据和接收控制指令信息,实时进行控制律解算,并输出各个通道的控制量。飞控计算机中实时运行控制律程序,将从各个传感器采集得到俯仰角速率、俯仰角、高度、速度以及从预期指令得到高度与速度指令输入纵向轨迹控制律,解算出升降舵偏转角度与油门调节控制量,驱动相应的舵机运动,进而改变无人机的高度、速度与姿态,在有限的时间和飞行距离内把这些参数与预期值的偏差调整到要求范围内,最终成功实现撞绳回收。
传感器的精度对于控制精度至关重要,高精度的传感器能够大幅降低控制律设计的压力,比如对于大型无人机来说,可以配置高性能光纤惯导来获得飞机姿态、角速度等的信息,配置军品级无线电高度表来获得高精度实时场高信息。但高精度传感器除了成本较高外,其重量与体积都较大,是总体成本较低的中小型无人机所不能负担的。对于文中介绍的总重只有50千克的天钩回收无人机来说,无论是成本还是带载能力均无法配置高性能惯导,只能配置重量仅有0.5千克的MEMS微航姿系统来获取无人机姿态与角速度信息,而精度相比惯导要低很多,为解决精度问题,此处放宽了姿态控制的要求,采用总能量控制方法实现高度与速度协调控制,同时把MEMS微航姿的姿态信息作为约束加入到控制系统中,以确保无人机的姿态安全。
对于实时场高的获取,由于没有配置无线电高度表,系统采用了卫星高度与气压高度融合的方法。即在进入回收前,首先判断卫星的可用性,若卫星高度可用,则将经过差分的卫星高度变换为相对地面的场高。由于卫星高度的连续性较差,需要使用气压高度进行融合,在融合之前,由于经过长时间飞行后,气压高度相对起飞前的基准漂移较多,需要首先用卫星高度进行一次标定,经过处理的融合场高兼顾了卫星高度的高精度与气压高度的连续性,完全可以替代无线电高度用于回收阶段的高度信号源。
2 控制律设计
2.1 控制对象数学模型的建立
由于文中研究的是纵向控制系统的设计,因此此处先简单阐述飞机的纵向运动。纵向运动只涉及纵向的运动参数与气动力,影响飞机纵向运动的外作用力主要包括如下。
1)发动机推力:方向沿发动机轴线,与机身轴线形成发动机安装角,一般发动机推力线不一定通过飞机的重心,此时推力还会产生力矩。
2)气动升力:垂直于飞行速度,向上为正,机身、机翼、尾翼等均可产生升力。
3)气动阻力:平行于飞行速度,向后为正,机身、机翼、起落架、飞机外挂物等均可产生阻力。
4)气动俯仰力矩:气动力在飞机对称面内对飞机产生的绕重心的力矩,抬头为正。
基于以上纵向作用力和力矩,首先需要建立固定翼无人机的小扰动线性化方程组[3],针对线性化模型设计控制律并对参数进行整定后,再引入到六自由度非线性模型中进行仿真验证[4],最终将固化的控制参数应用到飞行试验中。
无人机小扰动运动方程的推导有几个假设前提,包括:无人机是刚体,且质量为常数;忽略地面曲率,视地面为平面;假设地面为惯性参考系;假设重力加速度不随飞行高度而变化;无人机几何外形对称,且内部质量分布对称。
无人机动力学方程可由牛顿第二定律导出,基于机体坐标系可写出无人机合力与合力矩的表达公式,经过分解计算后可得到用无人机参数表达的3个方向的力以及绕机体3个轴的力矩动力学方程。为了描述无人机相对于地面的运动,还需建立机体轴系与地面轴系的转换关系,并建立3个姿态角变化率与3个角速度分量间的几何关系。以上描述所涉及的坐标系定义、推导公式等具体内容在文献[3]中有详细的阐述,此处不再赘述。
无人机运动方程组是非线性函数,为了既能简化方程又不失去构形参数起主导作用的影响,需要借助小扰动法使非线性方程线性化,并用解析法求解,这将有利于分析无人机本体及包含控制系统后的稳定性与操纵性。无人机的飞行运动可分为基准运动和扰动运动,将运动方程在工作点状态下做泰勒级数展开,将运动参数表示为基准运动参数和扰动偏移量之和。根据小扰动假设,略去二阶及二阶以上小量即可得到小扰动方程。将描述纵向运动的方程组做小扰动线性化,并整理为矩阵表达形式,可以得到纵向线性化状态方程,见下面的公式。其中Δθ、Δq、ΔV、Δα、ΔH分别为俯仰角、俯仰角速度、空速、迎角、高度;δe为升降舵偏角;状态矩阵和输入输出矩阵中的参数Ai为根据气动数据求出的各个系数。
(1)
上述系数矩阵的各参数为根据风洞试验数据插值或计算出的相应导数,系数矩阵的值随飞行状态的变化而变化,当状态确定时,飞行参数也随之为已知值,这些系数也就可以自动计算得到。飞行参数一般包括俯仰角、滚转角、航向角、俯仰角速度、滚转角速度、航向角速度、高度、速度、迎角、侧滑角、3个轴的加速度等。
基于小扰动方程的控制律线性化设计只是设计的第一步,虽然此时的控制律结构基本确定,但控制参数并不能适应工程化应用,因为无人机的运动本身是一个复杂的非线性运动,线性化设计可以确保系统是稳定的,但却无法确保全包线下无人机都能被很好的控制并具有良好的品质。一般线性化设计后确定的是控制参数的范围,完成线性化设计的控制律需要在六自由度非线性模型中进行验证与控制参数选优,该六自由度非线性模型框图如图2所示。
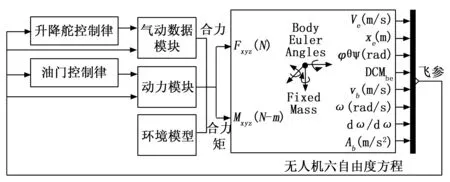
图2 无人机六自由度非线性模型框图
如图2所示,无人机六自由度方程即所构建的非线性方程,可以用MATLAB/Simulink模块搭建或直接调用Simulink中的已有模块。建立无人机六自由度模型的核心内容是通过气动数据模块、动力系统模块、环境模型得到机体产生的合力与合力矩。空气在无人机机体上产生的力和力矩包括:升力、阻力、侧力、滚转力矩、俯仰力矩和偏航力矩。其具体的计算方法如下式所示:
(2)
(3)
(4)
(5)
(6)
(7)
其中:ρ为空气密度,v为空速,S为参考面积,CL为升力系数,CD为阻力系数,CY为侧力系数,Cl为滚转力矩系数,Cm为俯仰力矩系数,Cn为偏航力矩系数,b为无人机翼展,c为平均气动弦长。通过风洞试验可以获得无人机飞行状态下的静导数、动导数和操纵导数,进而获得上述各气动力和气动力矩系数。据此可以建立计算模块,如图3所示。
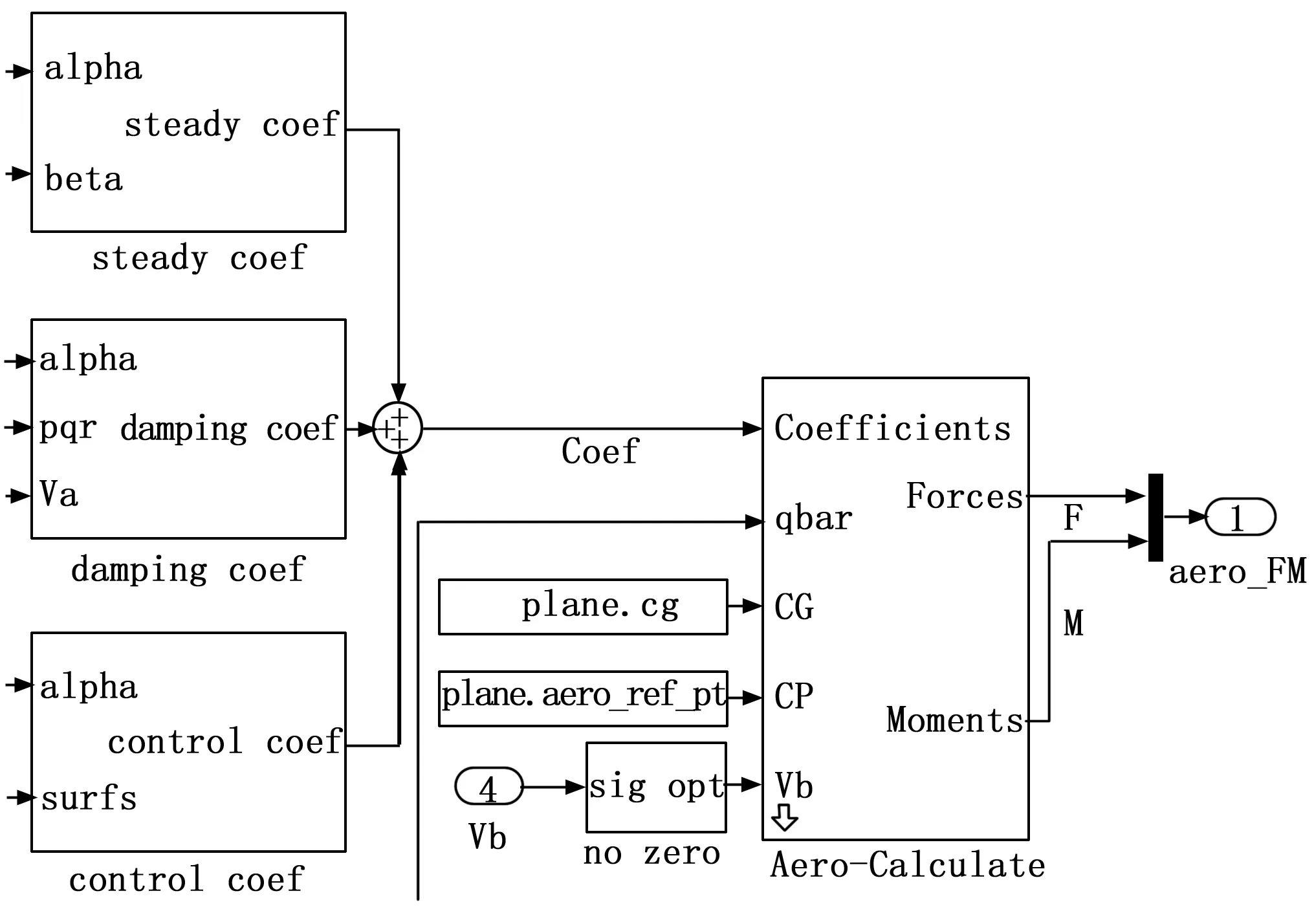
图3 气动数据模块
动力模块的建模主要考虑发动机和螺旋桨对无人机机体产生的推力/拉力以及反扭矩。使用测功机通过台架试验可以获得发动机在给定油门和转速下的输出功率数据。通过CFD计算流体力学或风洞试验的方法可以获得螺旋桨在不同前进比下的功率系数Cp和拉力系数Ct,进而计算对应的拉力和扭矩,如下式所示:
F=Ctρn2D4
(8)
M=Cpρn2D5
(9)
其中:ρ为空气密度,n为螺旋桨转速,D为螺旋桨直径。假设发动机产生的扭矩为T,而螺旋桨的转动惯量为J,则可以建立关于螺旋桨转动角速度ω的微分方程:
(10)
根据上述公式则可以建立动力模块的数学模型,如图4所示。
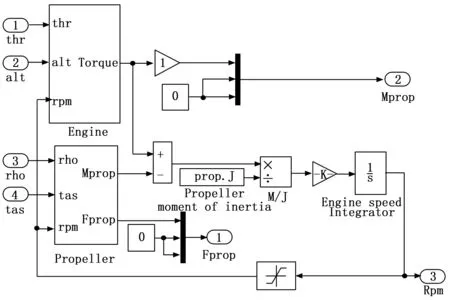
图4 动力模块
环境模块主要功能是实现根据地理位置和海拔高度的变化,实时插值计算当地空气密度、重力加速度等参数。这些参数将直接影响到作用于机体的气动力、力矩,以及重力等。标准大气模型(ISA)给出的空气密度随高度变化的曲线如图5所示。此外,在进行非线性仿真时,为了考核所设计控制律的鲁棒性,需要在环境模型中加入各种环境干扰,最常用的是阵风干扰和紊流干扰,可以使用数学模块搭建风干扰的数学模型,也可以直接选用Simulink中的现有模块。
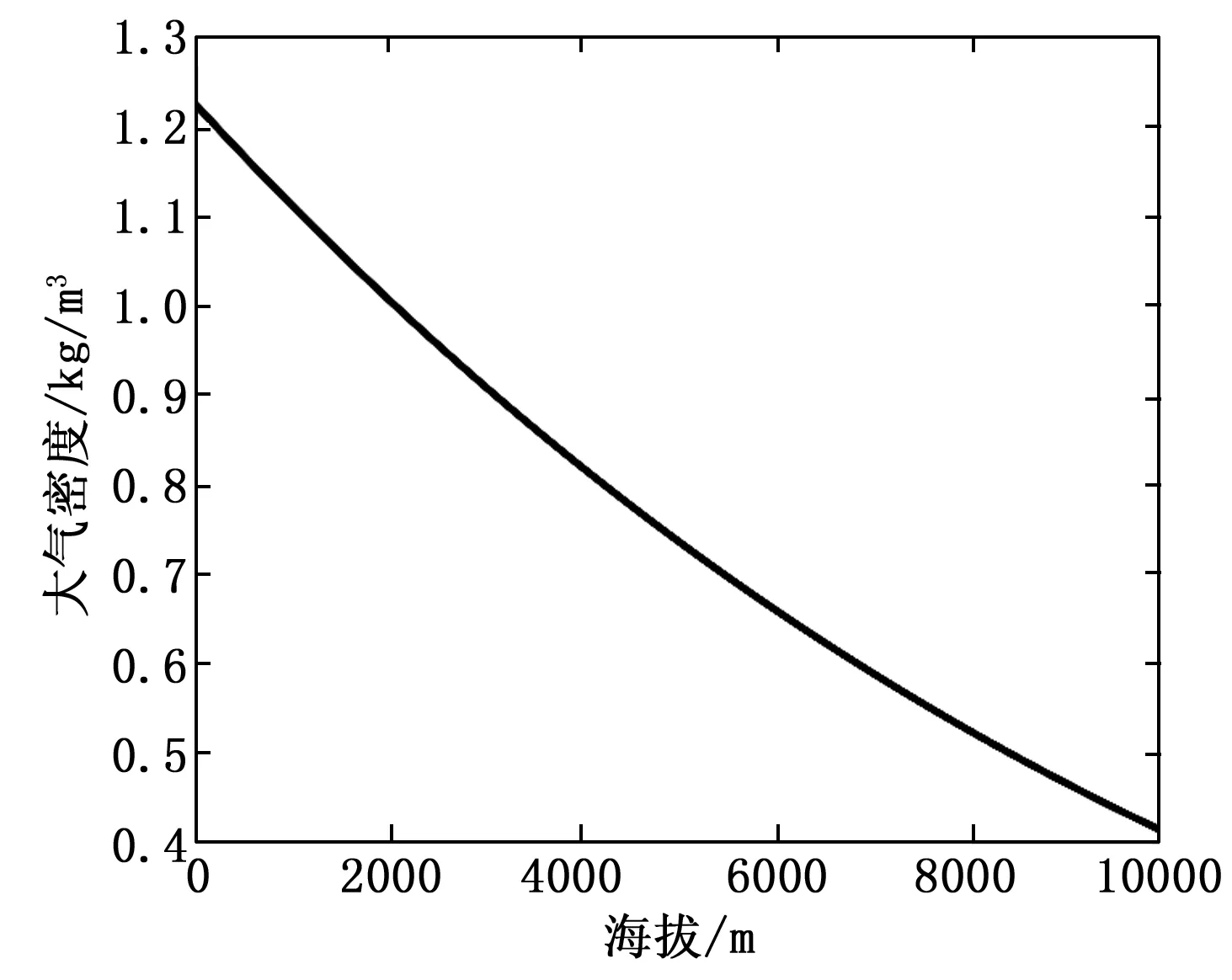
图5 空气密度变化曲线
将上述力和力矩输入六自由度方程模块即可建立描述无人机运动的非线性模型。该模型计算的飞行过程中的状态变量可输出为各飞行参数,这些飞行参数反馈到控制律模块解算执行机构的控制量,控制飞机飞行,如此就形成了仿真验证闭环。并可用于控制器参数整定优化和效果验证。
2.2 控制算法设计
无人机的飞行控制系统一般包括传感器、控制器与执行机构。控制算法经过代码实现后运行在控制器的实时系统中。控制算法一般为反馈控制,对于无人机的纵向控制来说,控制量一般包括升降舵控制与发动机油门控制,升降舵用于控制无人机的俯仰姿态以及高度的上升或下降,油门用于控制无人机的速度变化。升降舵的计算算法公式中包含的参数一般有俯仰角、俯仰角速度、高度、迎角等。对于不同的控制模态,所控制的参数也有不同,在天钩回收前的下滑阶段,以俯仰角控制为主,在天钩回收阶段,以高度控制为主,俯仰角则作为约束参数使用。无论哪种模态,角速度一般均作为阻尼参数引入反馈控制,以改善控制过程的品质。在追求稳态控制精度的天钩回收过程中,还需引入高度的积分控制。
此处纵向轨迹控制律的设计原则是在传统反馈控制[5-6]的基础上对高度与速度进行协调控制,此处引入总能量控制的思想[7-10]。
总能量控制(Total Energy Control)理论是波音公司提出的一种飞机综合飞行/推力控制系统。总能量控制的核心算法从控制飞机的能量变化率与分配率出发,从而实现对飞机飞行速度/航迹的解耦控制。
无人机控制油门的改变导致无人机推力的变化,同时会一定比率地改变飞机的总能量变化率,无人机的发动机油门控制量可作为总能量变化率的主控制量。升降舵偏转主要引起无人机俯仰力矩的变化,改变无人机的飞行姿态,在油门不变化时,推力不变,控制升降舵的偏转仅仅将无人机的动能与势能进行相互转换,改变总能量在动能与势能之间的分配关系,飞机的升降舵控制量可作为总能量分配率的主控制量。 总而言之,油门控制无人机总能量的变化率,升降舵控制只改变无人机的总能量分配率。
飞机在飞行过程中的总能量包括动能和势能,可以表示为:
(11)

(12)
使用升降舵调整无人机飞行的俯仰角大小,可以使得总能量在动能和势能之间转换但不会造成显著的总能量损失。相当于通过升降舵对动能和势能在总能量中的分配比例重新调整。而油门的改变会导致飞机总能量的变化。所以油门可以作为总能量的控制器,升降舵可以作为飞机动能和势能的分配控制器。
具体的总能量理论此处不再赘述,根据能量变化率、飞机纵向动力学方程等可设计出天钩回收过程无人机纵向控制律为:
(13)
(14)
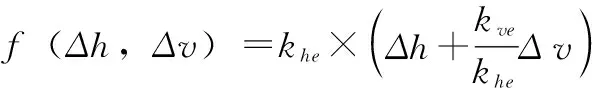
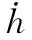
为了撞绳回收的安全,需要在距撞绳点一定距离时进行复飞判断。主要判断参数为高度偏差、速度偏差与航迹偏差,任意一个参数不满足要求则进行复飞,此时无人机会自动执行复飞控制策略。本系统的复飞控制策略中,无人机将进行25度滚转,同时使用最大油门进行爬升,具体纵向控制律为:
δe=kθ×(θ-θg)+kq×q
(15)
δt=δt_max
(16)
其中:θg=15°。δt_max为最大油门量,以使得无人机尽快爬升到安全高度,绕飞后将再次执行撞绳回收程序。
3 无人机天钩回收纵向控制策略与流程
天钩回收无人机的机翼翼尖处安装有满足强度要求的金属钩,回收过程中,当无人机的机翼撞击到捕获绳后,捕获绳会顺着机翼自然滑动至翼尖金属钩处,金属钩钩住捕获绳后,受冲击作用,捕获绳被卡紧在金属钩内,并通过限位卡片锁紧捕获绳,防止无人机滑落造成损伤。捕获绳合适的张紧力保证了无人机的动能能够被有效释放,又能确保无人机被捕获后不触地[11-12]。
图6为无人机天钩回收过程示意图。整个过程包括下滑、定高飞行、复飞决策、撞绳等飞行阶段。在定高飞行期间,无人机纵向控制律为具有俯仰角约束条件的高度与速度协调控制。

图6 无人机天钩回收过程示意图
天钩回收过程决策流程如图7所示。当天钩回收无人机进入回收模态后,无人机从当前高度下滑到撞绳高度,并在此高度上对准预期撞绳点保持定高飞行。当飞行至距捕获绳一定距离的决策窗口时,自动判断高度偏差、速度偏差以及航迹偏差是否满足窗口要求,任意一个要素不满足窗口要求则退出撞绳回收模态,复飞后再次进入回收。如果无人机到达决策窗口时所有要素均满足窗口要求,则继续保持速度约束下的定高飞行,直到机翼撞到捕获绳。在无人机撞上捕获绳后,无人机的速度将急剧降低,且在撞绳的瞬间,加速度会有突变,控制程序将根据速度、加速度的变化自动判断是否完成撞绳,一旦判断完成撞绳,则自动执行发动机停车指令,以确保无人机的安全。
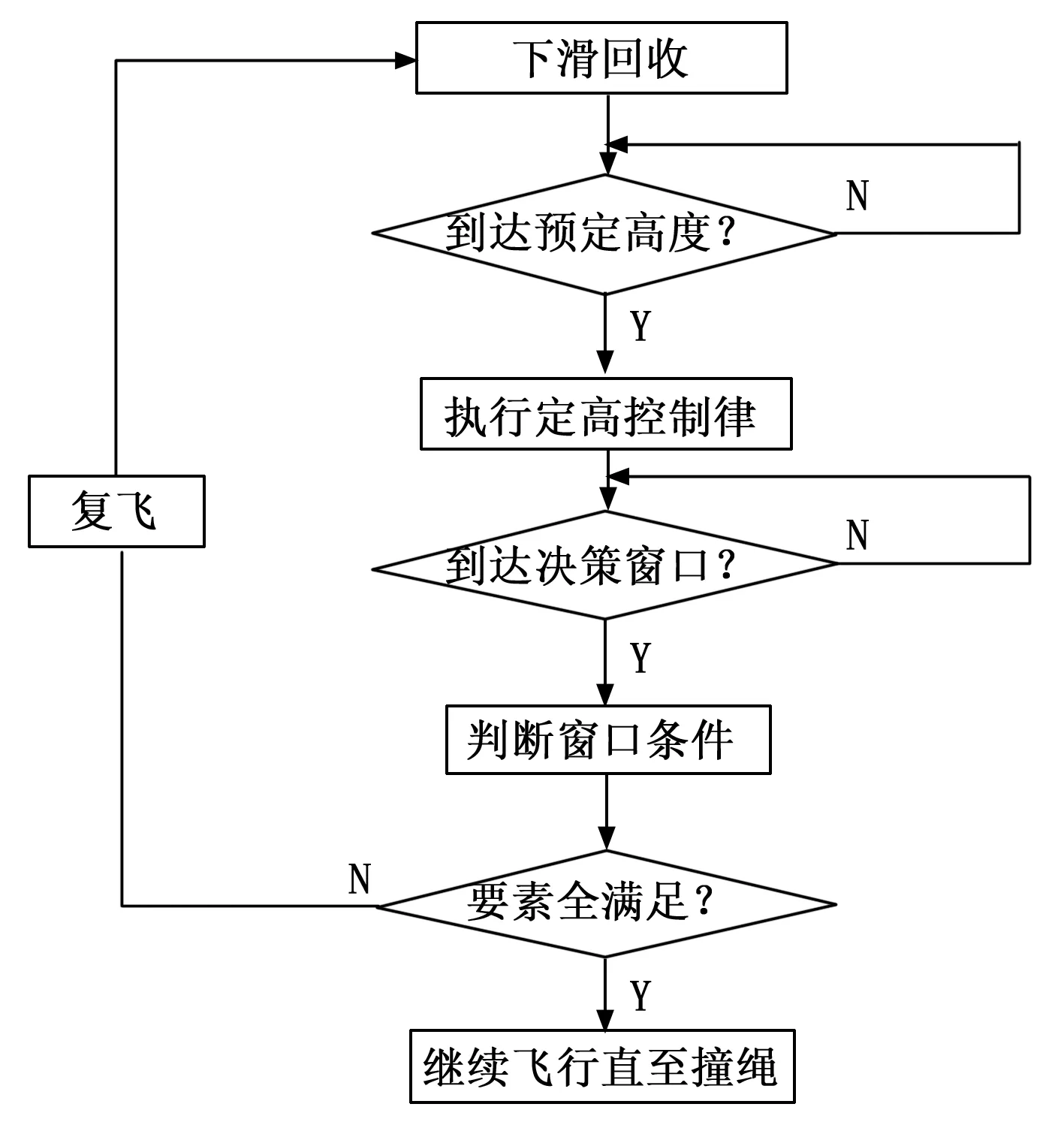
图7 无人机天钩回收过程决策流程图
4 设计验证与分析
本文的设计方法在某50 kg无人机上进行了应用,在完成控制律设计与实现后,构建了半物理仿真系统进行了综合仿真验证,在此基础上开展了飞行试验测试。
4.1 综合仿真验证
无人机系统综合仿真能够把飞控系统、航电设备、地面站、飞行控制与导航算法等形成闭环进行仿真验证[13-15]。得益于风洞试验数据,经综合仿真验证的程序可以直接应用于飞行试验。本文搭建的半物理仿真系统框架如图8所示。

图8 半物理仿真系统框架图
宿主机与目标机是所开发的仿真系统,首先在宿主计算机上建立无人机六自由度模型,并通过以太网网络将模型发送至实时目标机中。目标机中运行VxWorks实时操作系统,对模型进行实时解算,并把飞行参数回传给宿主机进行显示。仿真过程中,实时目标机通过AD采集卡接收舵机输出的控制信号进行模型解算,并将模型计算出的运动状态参数按照相应传感器的协议转换为各传感器的模拟数据发动给飞控计算机,接口可以是串口、模拟量等形式。例如将计算出的姿态角与角速度以微航姿的数据协议进行转换,将空速与高度以高度/速度传感器的协议进行转换,将地速与位置坐标等参数以卫星导航的协议进行转换。飞控计算机接收到这些传感器模拟信号后,与地面控制站所发的指令一同输入到控制律程序进行控制律的实时解算,并将解算结果输出给舵机进行相应运动,如此就形成综合仿真的闭环,通过这种综合仿真,除对闭环在内的硬件进行验证外,最主要的是能够完成控制律及其代码实现后的正确性验证。
由于无人机模型与实际飞机相比会有一定的差异,因此需要开展拉偏仿真测试,以验证控制律的鲁棒性,拉偏试验主要包括控制参数的拉偏仿真测试、无人机气动特性的拉偏测试以及动力系统的拉偏测试。此外,为验证系统的鲁棒性还可通过仿真模型注入各种干扰与故障,一般包括风场干扰、传感器通讯故障、执行机构故障、舵面损伤等。
利用所构建的仿真系统,分别在不施加干扰以及施加5米/秒阵风干扰的情况对天钩回收过程进行了综合仿真测试,参与闭环的实物包括飞控计算机、舵机、地面控制站与数据链,其中飞控计算机中运行飞行控制律代码。下面给出在施加了阵风干扰后的撞绳平飞段的相关参数,包括海拔高度、俯仰角、滚转角和空速数据。结果如图9所示。

图9 综合仿真数据曲线
仿真数据表明所设计的控制律可以准确控制无人机完成撞绳,且动态过程平稳。撞绳阶段高度波动稳定在0.5米以内,俯仰角约为1度,滚转角为0度,空速稳定在约105千米/小时。
4.2 飞行试验验证
开展飞行试验验证的系统包括无人机、地面控制站、弹射车、回收车、数据链系统与地面保障设备。其中,无人机的起飞重量为50千克,采用双尾撑、上平尾设计,翼展为4米。无人机采用气压弹射起飞,起飞后爬升至场高300米,完成矩形航线飞行后下滑至回收窗口,在控制律的作用下下滑至撞绳点高度后保持定高飞行,并最终完成天钩回收。
图10为所用的天钩回收装置示意图,最佳撞绳区域为捕获绳中间长度为1米的AB段,无人机天钩回收时若撞至该区域则无损伤风险。A、B点再各外延0.5米的区域为允许撞绳点,撞至该处存在机翼轻微损伤概率。其余区域为禁止撞绳点,撞击这些区域会造成机翼或机体损伤。

图10 天钩回收装置示意图
使用本文所设计方法成功完成了多次天钩回收,图11给出了3次实际撞绳位置(星号)与10次模拟撞绳位置(方框)分布图,模拟撞绳也是实飞数据,只不过在高于回收车30米处进入天钩回收程序,除了没有真正撞绳外,其他均与实际撞绳一致。

图11 撞绳位置分布图
由图11可知,3次实际撞绳点均在最佳撞绳区内,10次模拟撞绳有7次在最佳区域内,3次在允许区域内。
选取其中一次天钩回收数据,画出相应飞行参数曲线如图12所示,本次试验时风速在3米/秒至5米/秒之间。
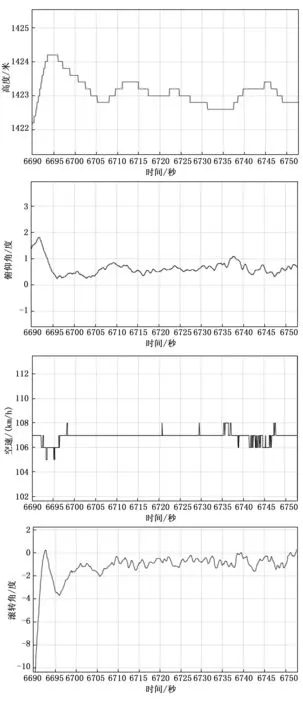
图12 撞绳时的高度与速度曲线
从图12结果可知,无人机能够在控制律的作用下实现顺利回收,且各参数均在要求范围内。最佳撞绳中心的高度为海拔1 423米,撞绳点位于最佳撞击区域内,撞绳时的速度稳定在106至108公里/小时,该速度处于允许撞绳速度与失速速度之间的最佳范围。飞机姿态基本水平,俯仰角与滚转角保持在0度附近。比较真实飞行数据与仿真数据可知,在真实飞行环境和带有噪声的传感器的条件下,飞行过程仍非常接近理想状态下的仿真飞行数据。相较于分别控制高度回路和速度回路的传统控制方法,该方法能够有效提高控制精度、消除或削弱外部干扰的影响,在存在噪声的低精度传感器的情况下具有更好的撞绳成功率和飞行平稳度。
5 结束语
文中针对某型固定翼天钩回收无人机提出了一种实用的天钩回收纵向控制方法,核心思想是利用总能量控制方法实现高度与速度的协调控制。给出了总体方案设计、控制系统组成、传感器数据融合策略、控制律设计方法以及在某50 kg级无人机上的应用结果。从综合仿真与飞行试验结果可知,该控制律设计方法正确可行、易于工程化实现,对于传感器的要求不高,能够实现天钩回收无人机回收过程的纵向高精度轨迹控制。所设计的方法已在多个项目中应用,取得了良好的效果。
