基于岭回归的河西走廊中部日光温室低温预测模型
2023-08-01白青华殷雪莲李学军
白青华,殷雪莲,2,王 静,张 洁,褚 超,李学军
(1甘肃省张掖市气象局,甘肃张掖 734000;2张掖国家气候观象台,甘肃张掖 734000)
0 引言
日光温室是北方地区进行反季节蔬菜生产的主要设施,日光温室主要热量来源是太阳能,通常以不加温的方式进行蔬菜等作物的栽培,因此室内的温度环境受当地的天气气候条件影响较大。地处河西走廊中部地区的甘肃省甘州区冬季低温期天气寒冷,日光温室低温冻害时有发生,是制约当地冬季设施农业发展的主要因素之一。农业气象服务部门具有室内外气象观测资料的积累,因此根据室内外气象要素研究探索当地日光温室低温预测模型在温室低温灾害防御中有重要的现实意义。
日光温室内外环境要素相互关系的研究已有不少,根据环境气象要素采用统计分析法进行预测模拟日光温室内温度等环境要素,回归线性建模是较为常用的一种方法[1],张磊等[2]分析了宁南山区日光温室内、外的最低气温的变化关系,建立了温室内最低气温的线性回归模型;戴明晶[3]建立了4种不同天气情况下日光温室低温预报的线性回归模型。关于温室低温预测的多元线性回归分析模型,忽略了线性回归分析中自变量存在的多重共线性对模型稳定性的影响。多重共线性使参数的最小二乘方差很大,各回归系数的符号可能出现错误的现象,其系数对样本数据的微小变化可能变得敏感[4]。处理共线性的方法常有主成分回归、岭回归、神经网络模拟法等,李宁等[5]应用主成分回归分析的方法,建立了日光温室内最低温度预报模型;金志凤等[6]构建了BP 神经网络模型,进行了杨梅大棚内气温预测。关于岭回归分析模型在日光温室低温预测中的应用目前还未见报道,岭回归是一种专用于共线性数据分析的有偏估计回归方法,本研究在选取预测因子进行共线性诊断的基础上,首次应用岭回归分析的方法构建日光温室低温预测模型,探索岭回归模型在日光温室低温预测中的模拟效果,创新日光温室低温环境要素模拟方法,同时为当地开展温室低温预测和服务提供依据。
1 资料与方法
1.1 资料来源
观测温室位于甘肃省甘州区党寨镇(100.29° E,38.53°N)内,当地气温最低月份为12月和次年1月,历年平均气温分别为-7.3、-9.1℃。日光温室坐北朝南,东西长80 m,跨度9 m,温室墙体为夯土墙体,温室前屋面采用聚氯乙烯薄膜覆盖,棚膜外覆盖保温被,根据天气情况每日早晚揭盖保温被,温室顶部设置通风口,冬季根据温室内温度状况一般午间进行通风。温室内种植作物为茄子。
温室内环境要素数据采集应用富景天策(北京)气象科技有限公司的“智慧园丁”设施农业监控系统,型号为SSR-ZGB-003。监测系统安装于温室中部,室内温度为距地面1.5 m处的温度,日光温室外的温度等数据资料来自张掖市气象局甘州区气象观测数据资料。
1.2 研究方法
选取2019年12月—2020年1月的数据资料中的9个气象要素作自变量,温室内最低温度作因变量,首先在进行自变量间的相关分析和多重共线性诊断的基础上,应用岭回归分析的方法建立日光温室低温预测的回归模型。利用2018 年12 月—2019 年1 月的实测数据资料与模型预测值进行模型精度检验。
1.2.1 预测因子的选取 选取2019 年12 月—2020 年1月当地最冷月份的气象资料,通过相关分析选取与温室内低温显著相关的气象观测要素作为预测因子,包括室外最高气温(TMax)、最低气温(TMin),前1日的室外平均气温(TMean-1)、最高气温(TMax-1)和最低气温(TMin-1)以及前1 日的温室内的最高温度(Tmax-1)、最低温度(Tmin-1)和平均温度(Tmean-1)。天气状况影响温室接受的辐射量,影响温室内温度[7],为了区分室外天气状况,同时将总云量(N)也选作预测因子。
1.2.2 多重共线性诊断 多元线性回归分析中,由于多个自变量间相互作用和影响,往往存在共线性关系。所谓共线性,是指2 个或多个自变量间存在高度相关关系。共线性造成的主要后果是自变量对预测变量的估计不可靠,因此多元线性回归分析中有必要进行共线性诊断。自变量间的相关系数矩阵可作为多重共线性的初步判断依据,再结合容忍度(TOL)和方差膨胀因子(VIF)作为诊断多个自变量间共线性的严重程度[8]。当自变量容忍度(TOL)小于0.1,方差膨胀因子(VIF)大于5(或大于10)时,表明自变量间存在严重的多重共线性。
1.2.3 岭回归模型的建立 岭回归,又称脊回归,是对不适定问题进行回归分析时经常使用的一种正则化方法,是对最小二乘回归的一种补充,岭回归通过损失无偏性来换取高的数值稳定性,从而得到较高的计算精度。根据已选定的预测因子组成观测阵X和日光温室低温观测向量Y,当自变量存在共线性时,即∣XTX∣≈0,假设XTX加一个正常数矩阵kI(k>0,I为单位矩阵)[9],得到岭回归的估计量如式(1)所示。
将式中y的各分量作为k的函数,当k在[0,+∞]变化时,在平面直角坐标系绘出岭迹图[10]。岭迹图可直观体现出各自变量因子对变量的相互作用关系,根据岭迹图得到各预测因子的系数后建立岭回归模型。
1.2.4 预测模型检验 通过模型预测值与实测值的比较进行模型的应用精度检验,本研究采用了3 个评价指标:预测值与实测值的绝对误差(≤3℃)的准确率[1]和决定系数(R2)、均方根误差(RMSE)[11],R2越接近1,表明模型吻合度越高,RMSE越小,表明模型偏差越小。
1.2.5 数据处理 采用DPS9.05数据处理系统进行共线性诊断和岭回归分析等数据处理,运用相关分析和多元线性回归等统计方法进行数据分析。
2 结果与分析
2.1 预测模型各变量间的相关性分析
日光温室内部最低气温除与室外大气环境的温度有关外,根据温室温度的日变化[12]可知,温室的最低气温出现于清晨揭帘前,主要受到前一日气象因子的影响,日光温室的基础气温对次日揭帘前的温度具有决定性作用。因此选取当日室外最高、最低气温(TMax、TMin)的同时,选取了前1日温室最高、最低和平均温度(Tmax-1、Tmin-1、Tmean-1)以及前1日室外平均、最高和最低气温(TMean-1、TMax-1、TMin-1)作为预测因子。由表1可见,当天最高、最低气温(TMax、TMin)与温室内日最低气温(Tmin)极显著相关,以当天最低气温对温室最低气温(Tmin)影响最为明显,温室的基础气温(包含Tmax-1、Tmin-1、Tmean-1)和决定温室基础气温的室外温度(TMean-1、TMax-1、TMin-1)对温室低温(Tmin)的影响也表现出显著的正效应。天气状况影响温室接受的太阳辐射量,影响温室内温度[7],通过表1分析,当日总云量(N)与温室最低气温(Tmin)也有一定程度的相关性,将总云量(N)也作为预测因子,区分室外天气状况同时,提高预测模型的稳定性。
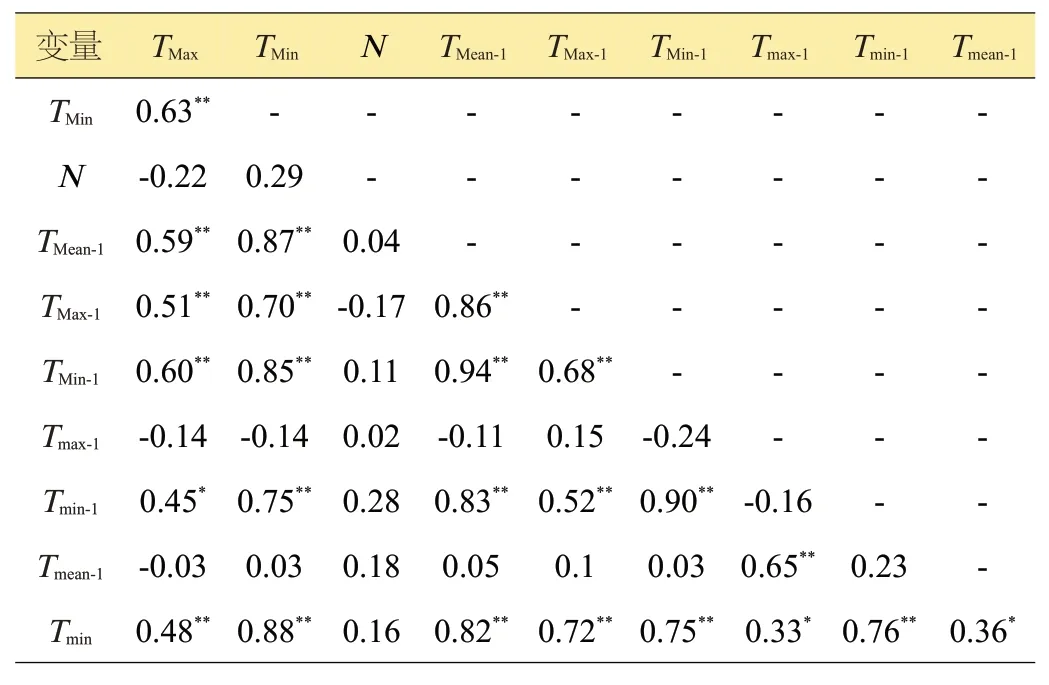
表1 日光温室低温及预测因子间的相关系数
从表1温室低温(Tmin)与各预测气象因子的相关性分析表明,可以对日光温室最低气温用这些预测因子作为自变量进行多元线性回归建模预测。表1还显示出各预测因子之间存在不同程度的相关性,推断所选预测因子之间存在多重共线性问题。
2.2 预测因子间多重共线性诊断
进一步将上述多个预测因子作自变量,温室低温(Tmin)作因变量建立多元线性回归方程,进行多重共线性诊断。表2显示了用最小二乘法构建温室最低气温(Tmin)的回归方程参数估计及预测因子的共线性统计量。检验结果显示回归方程的R2=0.9302,预测因子TMax、N、TMean-1、TMax-1、TMin-1、Tmax-1、Tmin-1的偏回归系数均未通过统计学检验,其对日光温室低温的作用在α=0.05水平上不显著,不具备统计学意义。自变量TMax、N、TMax-1、TMin-1的偏回归系数符号为负值,与相关分析的结果不一致。结合共线性统计量亦看出,TMean-1、TMax-1、TMin-1、Tmin-1的容忍度小于0.1,方差膨胀因子(VIF)均大于10。综合上述分析,选取的预测因子间存在较强的多重共线性问题,可采用岭回归分析方法建立模型。
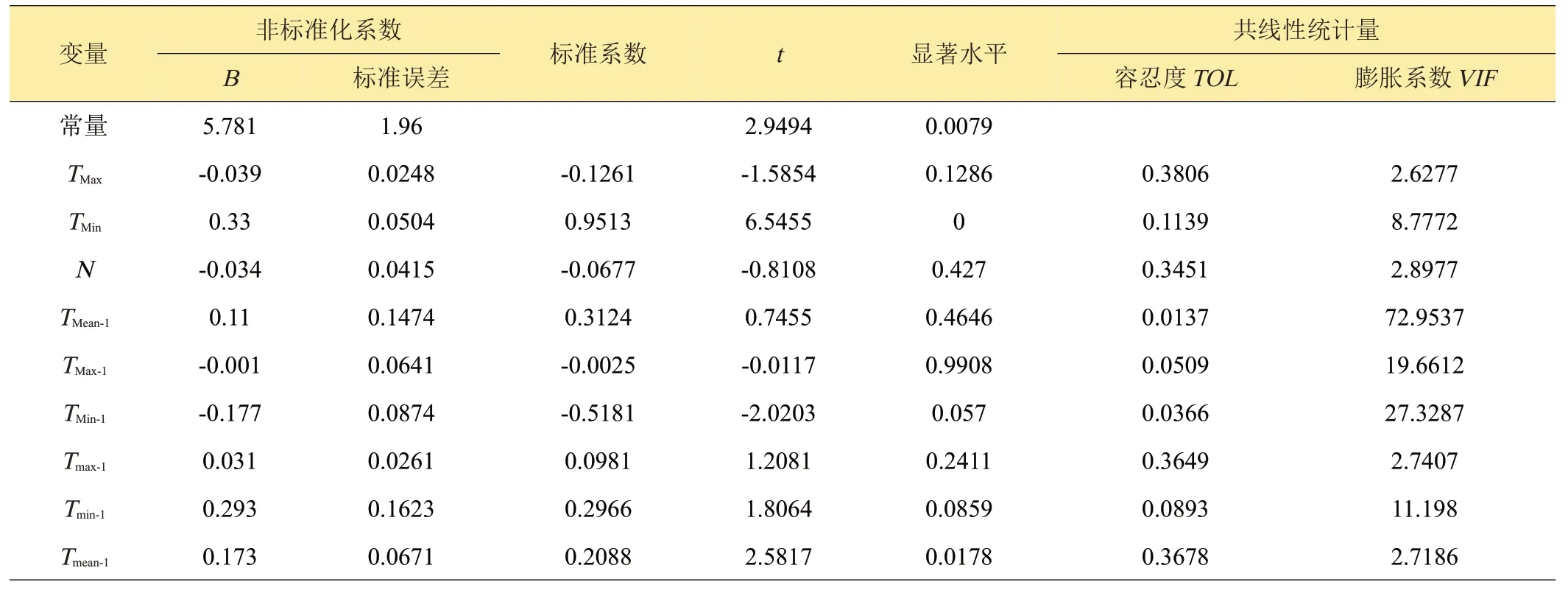
表2 最小二乘多元线性回归参数估计及共线性统计量
2.3 岭回归模型的建立
将所选9个预测因子和温室低温(Tmin)用DPS软件做岭回归分析,以岭参数k为横轴,以各预测因子的标准回归系数估计值为纵轴,得到关于k的岭迹图[13-14]。由图1可看出,当k值从0变化到1时,各温室低温预测因子的标准回归系数均随岭参数k的增大而趋于稳定。在岭迹图上,当k=0.2时,各预测因子的回归系数开始趋于稳定,取岭参数为0.2时的模型标准化组合作为日光温室低温(Tmin)的预测模型,如式(2)所示。
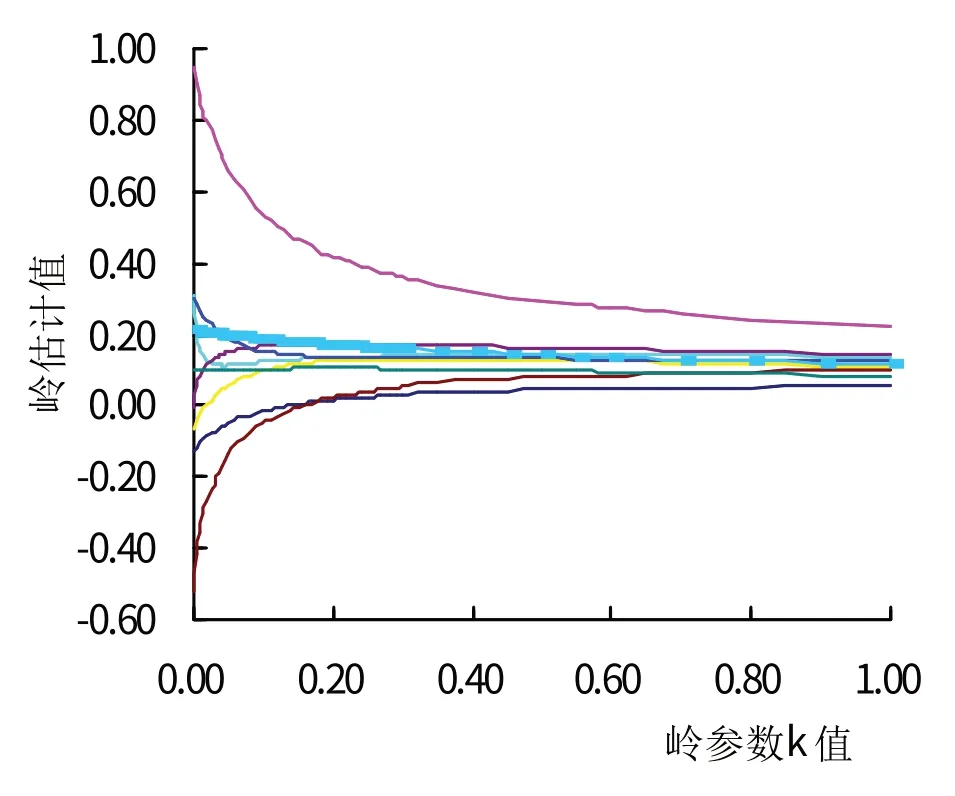
图1 岭回归分析的岭迹图
该预测模型R2=0.9105,略小于最小二乘模型,F=22.5976,P=0.0001 高度显著,拟合效果较好。岭回归模型中各预测因子的回归系数的符号均为正值,这与相关分析的实际情况吻合,各预测变量的系数较为合理。表明当预测因子变量存在共线性时,应用岭回归分析的方法建立的模型能够克服共线性的影响,同时保留全面的预测因子信息,保证了模型的稳定性,能更有效准确地对日光温室低温进行分析预测。将标准化方程转化得到日光温室低温的最终预测模型,如式(3)所示。
2.4 模型检验评价
为了验证模型的实际应用效果,选择未参与建模的2018 年12 月—2019 年1 月温室内外气象要素观测资料进行验证,构建模型的资料不参与验证。图2 通过日光温室低温模型预测值与实测值比较可看出,当地观测温室最低温度约从12月20日后开始下降,至次年1月10日温室低温总体维持较低水平,之后温室低温开始回升,模型预测值与实测值二者变化趋势趋于一致。通过比较模型预测值与实测值的绝对误差[1],小于1、2、3℃的准确率(≤1℃、≤2℃、≤3℃)分别为87.1%,95.2%,98.4%。进一步结合图3 可看出模型预测值与实测值之间存在较好的线性拟合关系,通过计算预测值与实测值间R2为0.8543,RMSE为0.7849℃。综上,岭回归预测模型应用检验效果良好,模型准确度较高,可以应用于当地日光温室的低温预测。

图2 日光温室低温预测值与实测值比较
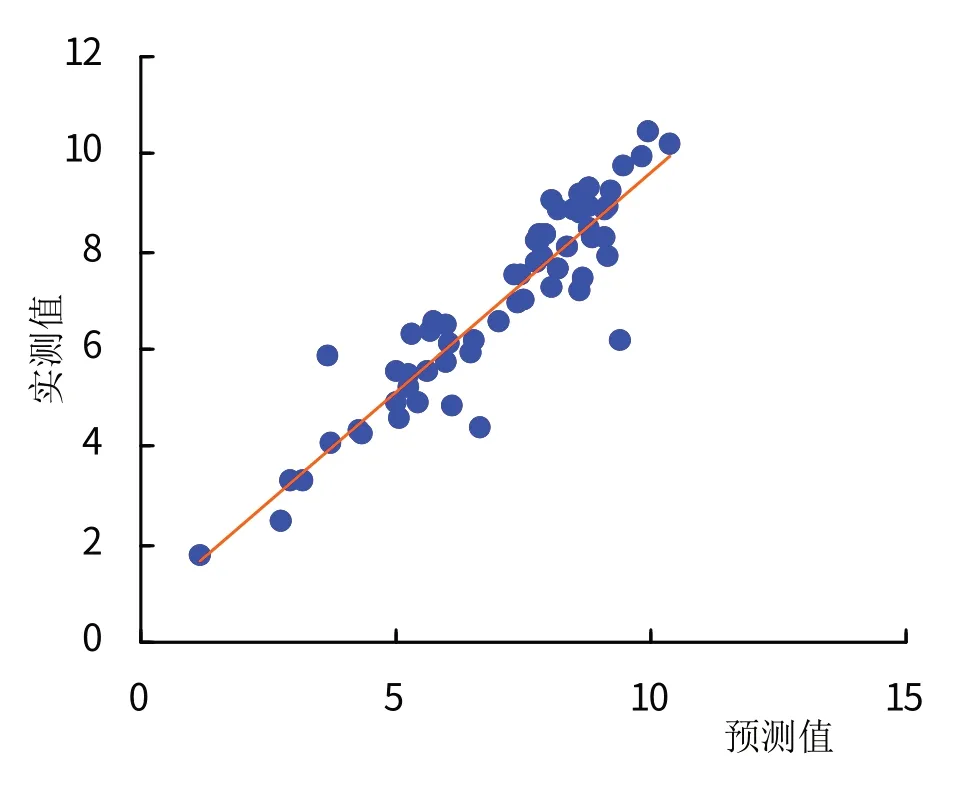
图3 日光温室最低气温的预测值与实测值线性关系
3 结论与讨论
(1)应用岭回归分析的方法构建日光温室低温预测模型是可行的。日光温室内外环境要素之间大多相互作用、相互影响,本研究筛选的日光温室预测因子间存在较严重的共线性问题,岭回归法处理自变量间的共线性效果较好[15],应用岭回归构建的日光温室低温预测模型全面保留了自变量信息,使模型的稳定性更好,模型通过了统计学检验,并进行实际验证后准确率高,预测值与实测值之间拟合度高,模型偏差小,精度较高,适于当地同类型日光温室开展低温预测。
(2)针对不同类型的预测模型,模型构建方法的选择十分重要,当自变量间存在多种共线性时直接利用普通最小二乘法构建的日光温室低温预测模型,使一些自变量回归系数的符号正负号倒置,无法通过统计显著性检验,降低了回归模型的应用价值。岭回归分析是一种专门用于共线性数据分析的有偏估计方法[16],岭回归使得回归系数的符号趋于合理,更符合实际,这一点在本研究中也得到了验证。岭回归模型在构建过程中岭参数k的取值具有主观灵活性,对模型的影响较为关键[9],但这种人为机动性有利于发挥定性与定量的有机结合[16],只要岭参数k取值合理,岭回归在解决日光温室自变量间的多重共线性问题会发挥出独特的作用,取得较好的预测效果。
(3)预测因子的选取在一定程度上影响模型的精度,在预测因子选取时既要考虑对模型精度的影响,还要考虑模型的实际适用性,基于气象要素预测日光温室内低温,本研究通过相关性分析筛选出9 个因子对温室低温进行预测,其中除总云量外,其他预测因子与温室低温均显著相关,该模型将天气状况(晴天、阴天、多云)影响因子(总云量N)考虑纳入模型,在实际应用中不再区分天气状况分别建模,而是将不同天气条件下的温室低温预测统一于一个模型,在进行温室低温预测时不用根据天气状况分别建模和计算,简化了模型计算过程,可操作性强,该模型利用当地气象要素观测资料结合天气预报中的最高和最低温度可对日光温室低温作出预测。
(4)日光温室保温性能影响因素较多[17],对于特定温室,种植户通风,保温被揭盖等常规管理中人为因素对温室蓄热保温量也有一定影响。本研究在资料选择方面筛选了12 月1 日至次年1 月的观测资料进行建模,一方面是因为根据甘州区历年天气资料发现该时段是当地一年中温度最低时期,另一方面,种植户在低温期为了尽量保证温室较高的热量状况,最大程度地做到温室内保温蓄热,种植户根据外界天气条件,适时通风、按时揭盖保温被等,预防低温对温室作物的不利生长影响,在此低温期间种植户采取的温度管理调控措施在时间和要求上相对严格和精细。在不同外界温度条件下由于温室保温管理要求和精细化程度不一致而造成对温室低温影响程度也不一样,筛选同处于低温期的资料建模,考虑到温室温度管理在时间和措施上一致性强,人为管理因素对温室低温的影响程度差异性相对较小,故选择该时期资料建模是合理的。通过模型检验也看出该模型精度较高,适于开展当地低温期的温室低温预测和服务。由于气候条件、温室结构、种植管理习惯等因素的差异,对于其他地区温室,还需根据特定的温室类型,选择适合的预测因子和与之相对应的预测方法建模进行低温预测和开展设施农业气象服务。
