面向车辆驾驶模拟器的路面谱仿真

刘 远，刘永亮，朱 胤，陈 云，张智锋

（北方自动控制技术研究所，太原 030006）

0 引言

仿真技术作为传统的科学理论分析和实验研究分析之外又一重要的系统分析方法，被誉为是当前数字化背景下的产业技术“跨越式发展工具”，尤其在模拟训练、载人航天、作战对抗等复杂高维问题领域，仿真技术的作用被逐渐发掘出来，其扮演的角色也慢慢从被动变为主动、从静态变为动态。基于驾驶模拟实物（live）、虚拟场景（virtual）、路面扰动构造模型（constructive），构建真实的战场驾驶环境，针对现实环境下装甲车辆驾驶中的路面扰动、车辆动力学特性、人体感知特点等复杂因素引起的综合振动效果，研究高逼真度的路面谱振动仿真模型，是提高模拟训练装备训练沉浸感和训练效果的有效途径之一。此外，驾驶模拟器逼真度研究也为研究驾驶员行为特征和开发智能评估算法开拓了思路。

出于经济、环保和安全等因素的考虑，驾驶模拟器一直是教学和驾驶员技能训练的重要工具。驾驶模拟器有多种类型从仿真逼真程度来看，可以分为“低级”“中级”“高级”［1］，其中，“低级”驾驶模拟器利用计算机屏幕显示驾驶场景，并通过设置方向盘和踏板进行驾驶模拟；“中级”驾驶模拟器一般通过一个驾驶座舱实现，在驾驶舱内有方向盘和踏板，并装有仿真的仪表盘等设备。这两类驾驶模拟器主要是对道路、行人、天气等视觉元素进行了视景模拟，驾驶员以模拟场景为信息导向进行驾驶训练，因此，很多国内外学者针对不同车型，设计了该车型的驾驶模拟器视景系统［2］，得益于信息技术的快速发展，图形渲染质量不断提高［3］，驾驶视景仿真的逼真度也得到了明显的提高，但是这两类模拟器却忽略了汽车行驶途中运动状态的变化以及由不同路面的颠簸对驾驶员的操纵带来的影响，没有对车辆动力学进行模拟，只对视觉信息进行了模拟［4］；“高级”驾驶模拟器中与前两者的区别主要是加入了体感维度的仿真，即使用运动平台对汽车运动姿态进行模拟。现阶段的“高级”驾驶模拟器主要使用多自由度运动平台对车辆的运动状态进行模拟复现，但大多数驾驶模拟器只能定性地对斜坡、弯道、路面大幅度的不平整等低频信号进行复现，对于真实行驶过程中，由路面、发动机、悬架共振等引起的高频振动带来的驾驶体感，却不能有效复现［5］。增加不同等级路面的高逼真度模拟不但可以增强驾驶“沉浸感”，而且对于提高驾驶模拟器逼真度，进而提升模拟训练效果和训练效率意义重大。

本文对常见等级路面进行统计特性分析，并基于谐波叠加法对A-D 级［7］路面进行建模仿真；将各级路面的随机平稳信号作为初始驱动信号驱动Stewart 六自由度运动平台，实现对路面扰动效果复现，利用安装在运动平台上的九轴航姿传感器，采集振动信号；对采集到的信号进行时频分析，重构功率谱密度特性，并与国际标准中的同等级路面功率密度谱数据进行比较，研究振动机构在复现过程中的频响特性，修正输入数据，实现运动平台对真实路面的复现，可以用于轮式和履带式半实物驾驶模拟器的路面模拟。

1 路面统计特性分析

要对真实道路进行模拟，进行路面谱建模，路面不平度是不可忽略的一个重要因素。国内外相关研究表明，路面作用于车轮产生的随机扰动属于各态历经的随机平稳过程［6］。路面不平度一般使用频域中位移功率谱密度对其统计特性进行描述。

根据国标等相关文件所建议［7］，路面位移功率谱密度Gq（n）用下式作为拟合表达式：

式中，n 为空间频率（m-1）；n0为参考空间频率，n0=0.1（m-1）；Gq（n0）为路面不平度系数（m2/m-1）；w 为频率指数，根据标准，取w=2。

按照上述标准，基于各种路面不平度系数的不同，研究人员将路面分为A～H 8 个等级。8 个等级路面不平度系数Gq（n0）如表1 所示。

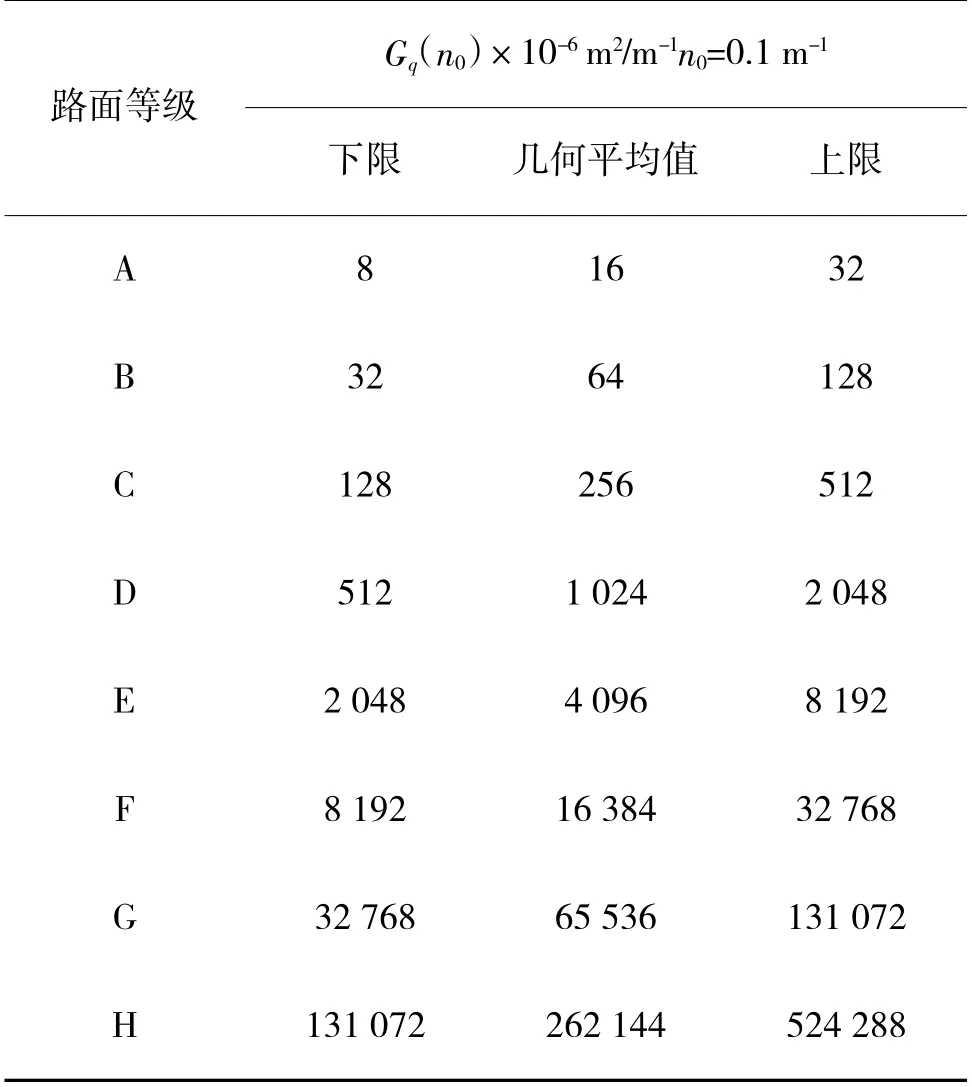
表1 各等级路面不平度系数Table 1 Roughness coefficient of each grade of road surfaces

2 路面不平度数值计算算法

数值法对路面谱进行建模计算得到大家的普遍认可，常用的方法有谐波叠加法、滤波白噪声法、傅立叶逆变换法和ARMA 模型方法［8］。其中，谐波叠加法基于三角函数求和，当空间频域划分数达到一定值时与真实道路可完全等价，适用于任意路面的数值模拟，有较好的适应性和精度，本文基于该方法，实现对路面振动信号和模拟器复现信号的时频转换和数据分析。

车辆产生的振动不仅与道路本身有关外，还受到车速u（m/s）等因素的影响，输入的时间频率f（Hz）与空间频率n（m-1）满足以下关系：

此外，真实道路的输入一般都是在时域中表示的，根据帕斯瓦尔定理和维纳——辛钦定律可得：

在某一频率区间f1≤f≤f2内，将其划分为N 个等分区间，用每个区间中心点处频率fmid_i对应的功率谱密度近似作为整个区间的功率谱密度，则在第i 个区间内有

根据平稳随机过程的性质可得，第i 个区间的路面不平度可以用标准差为σq的正弦波函数表示，即

其中，qi为第i 个区间的随机扰动；θi为区间［0，2π］上的随机数。

于是，该频率区间的路面不平度q（t）就可以由下式求得：

上述即为谐波叠加法的数值模拟思路［9］。

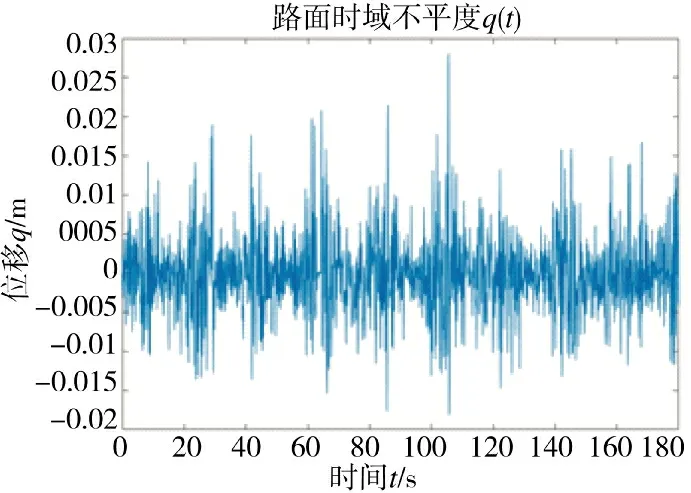
本文对A～D 级常见路面进行计算仿真，其中，B级和C 级路面的仿真路面不平度结果如图1 所示。空间频率取［0.05，2.83］，划分区间个数为N=2 000，车速分别为u=20 km/h 和u=30 km/h。

图1 路面不平度仿真结果Fig.1 Simulation results of roughness of road surfaces

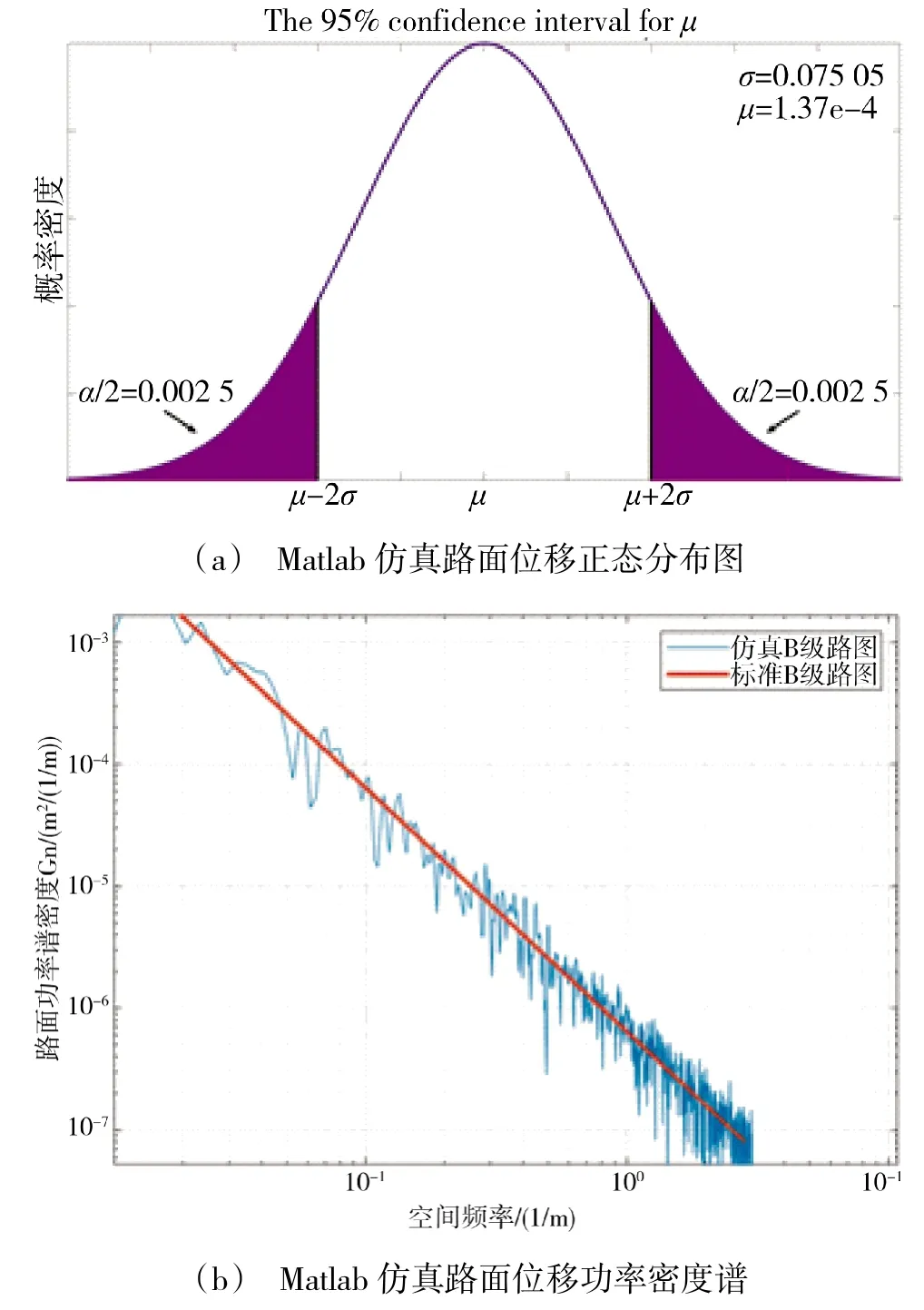
图2 B 级路面仿真路面谱统计特性Fig.2 Statistical characteristics of B-level road surface simulation road surface spectrum

由图1 仿真结果分析得出，道路等级越高，路况会变差，路面不平度也随之加剧，与国家标准中描述的情况相符，而且对于同一等级的道路路面，随着车速的增加，路面的不平度也会在一定程度上加剧，结合前述的路面位移功率谱密度表达式不难分析出产生此现象的原因：在时域中，输入的频率f一定时，由式（3）可以得出，当车速u 增加时，路面位移功率谱密度会随之增大，这也就意味着路面不平度的加剧。

对上述B 级路面数据进行统计特性分析可知，其位移均方根值为ψq=7.51×10-3m，路面位移功率密度谱在标准B 级路面位移功率密度谱曲线上下波动，趋势一致，说明由谐波叠加法仿真得到的路面不平度可以很好地反映标准B 级路面功率谱的统计特性，可以作为驱动信号输入到运动平台对B级路面进行复现。

3 运动平台参数选择

要想实现路面谱高逼真程度的仿真复现，对运动平台的设计和参数选择有一定的要求。下面论述基于路面谱复现的运动平台参数的选择理论和方法。

由于路面不平度属于平稳随机过程，其期望μ=0，于是它的均方值ψ2等于方差σ2，可以得到下式：

同时，加速度功率谱与位移功率谱的有以下关系：

可以得到下式：

式中，nmax，nmin为空间频率的上下限；ψq为位移均方根值；ψa为加速度均方根值。

根据式（7）～式（9）及表1 的数据可以计算得出如表2 所示的A～H 级路面的位移均方根值和加速度均方根值：

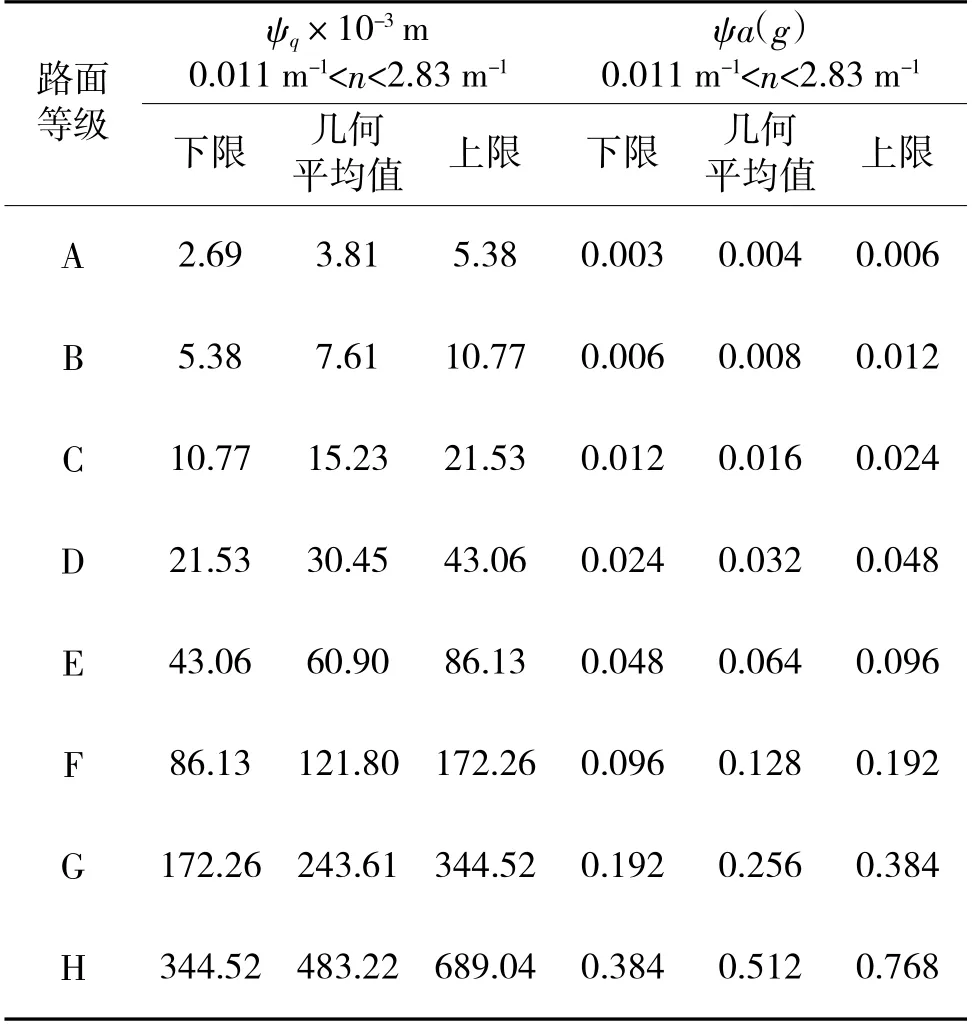
表2 各等级路面位移、加速度均方根值Table 2 Root mean square value of road surface displacement and acceleration at each level

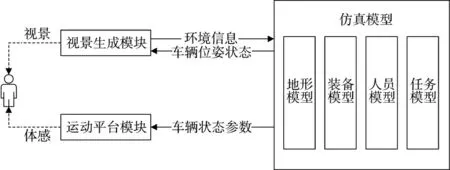
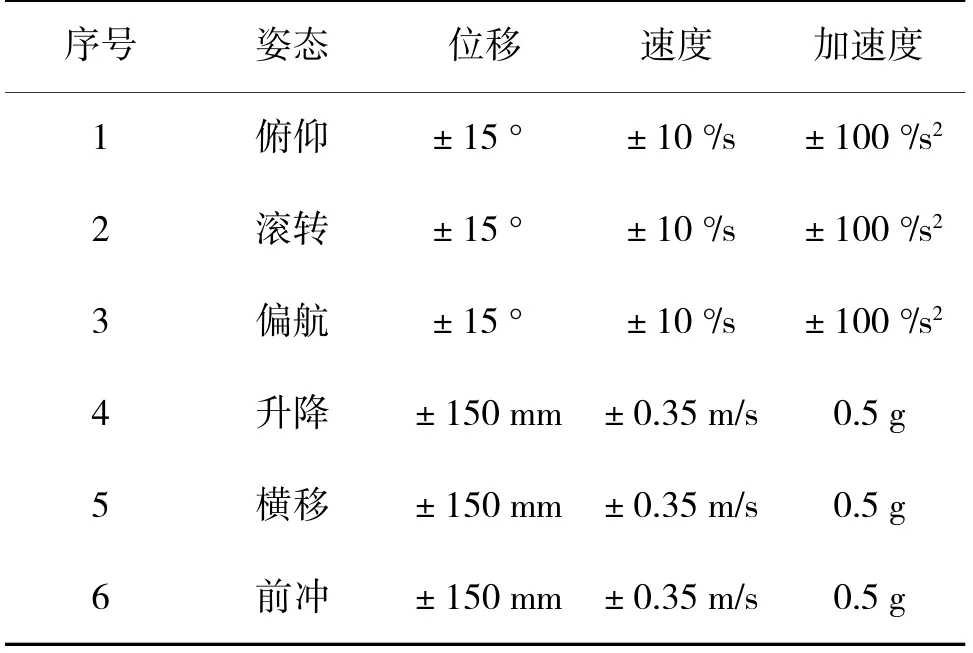
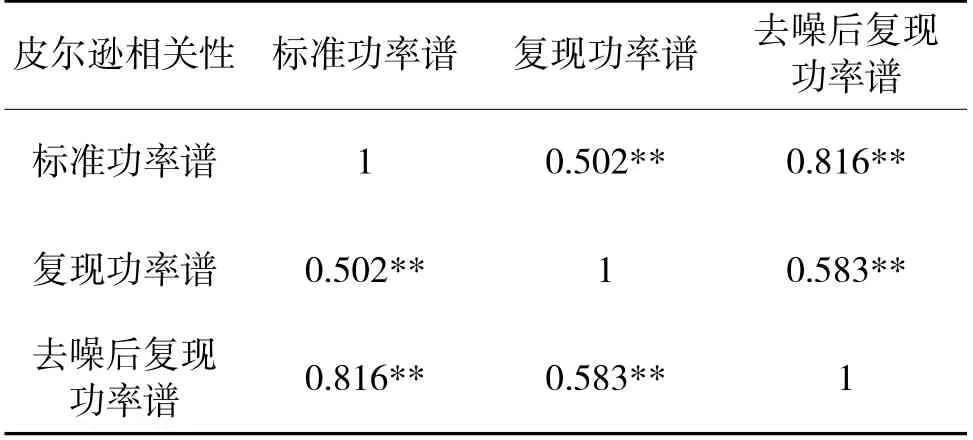
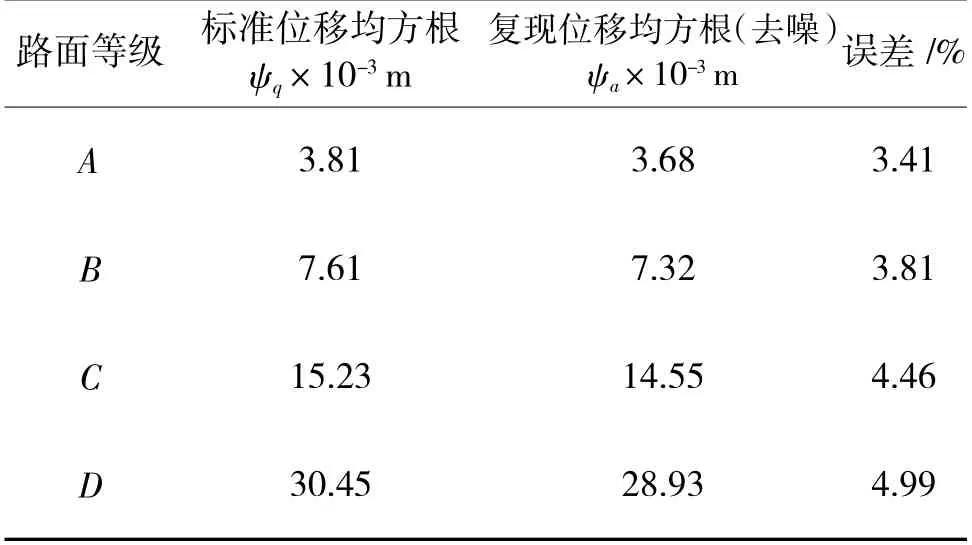
常见道路统计特性分析的空间频率一般在0.011 m-1

由上述的道路统计特性分析可以得到基于路谱复现的运动平台的参数选择参考如下：

1）行程范围选择。由平稳随机过程的统计特性可知，最值在3σq范围内的概率为95%，根据表2 的各级路面不平度随机扰动的位移均方根值ψq可得运动平台的行程R 范围应为［-3ψq，3ψq］；

2）加速度范围选择。同行程范围选择的原理相同，根据表2 可得运动平台的加速度a 范围应为［-3ψa，3ψa］；

3）工作频率范围选择。根据上文空间频率与时间频率转换关系，并考虑车辆悬挂和非悬挂部分的固有频率，运动平台的工作频率f 范围应为0～50 Hz。

4 路面不平度输入及振动信号采集

车辆驾驶模拟器的运动复现，主要是基于车辆动力学模型与场景中的地形道路模型实时交互，动态地产生道路颠簸振动效果，并将车辆状态参数反馈给振动执行机构，形成与视景模块相一致的驾驶效果，给驾驶员以逼真的驾驶体验，模拟过程如下页图3 所示，视景生成模块将环境信息传递给仿真模型，仿真模型再将车辆位姿状态反馈回视景生成模块，并将车辆状态参数提供给运动平台模块，使驾驶员感受到真实的驾驶体感。

图3 驾驶模拟器运动系统动感模拟过程Fig.3 Dynamic simulation process of driving simulator motion system

本路谱数据直接通过控制计算机输入运动平台进行路面谱模拟，所使用的Stewart 六自由度运动平台如图4（a）所示，平台采用伺服电动缸驱动，伺服电动缸的活塞杆与上平台通过虎克铰相连。运动平台用于提供实现路面不平度复现振动过程中的动力输出，并采用九轴航姿传感器（型号XSENS MTI300），如图4（b）采集运动平台Z 方向的振动数据。

图4 实验设备及实验原理图Fig.4 Schematic diagram of experimental equipment and experimental principles

图5 加速度传感器参数设置界面Fig.5 Acceleration sensor parameter setting interface

图6 Z 向振动加速度采集界面Fig.6 Z-direction vibration acceleration acquisition interface

实验用Stewart 六自由度运动平台参数如表3所示。

表3 运动平台参数Table 3 Motion platform parameters

在MT Manager 软件中设置加速度传感器的采样频率，将路面不平度数据信号输入到运动平台，并使用加速度传感器对运动平台Z 方向的振动加速度进行采集，实验原理如图4（c）所示。

5 数据分析

由Matlab 仿真所得B 级路面的位移均方根值为ψq=7.51×10-3m，由平稳随机过程的统计特性可知，峰值有95%概率落在［-3ψq，3ψq］范围内，故数据有效。对采集到的振动加速度进行积分处理，得到运动平台所模拟的路面不平度如图7 所示，路面不平度的数值基本在［-0.02 m，0.02 m］之间上下波动，路面不平度复现的概率密度分布函数如图8 所示，呈正态分布，与路面随机扰动平稳随机过程的统计特性相一致。

图7 运动平台复现路面不平度Fig.7 The motion platform reproduces the roughness of the road surfaces

图8 复现路面不平度正态分布图Fig.8 Normal distribution map of reproducing the roughness of the road surfaces

由于人体对低于一定频率的运动信号不敏感，而且视觉对于低频运动信号的感知有补充作用，不模拟低于一定频率的运动信号也能模拟出逼真的运动感觉［10］，由于成本和实验条件的限制，实验所用运动平台的额定最大工作频率Hzmax为10 Hz，对于高出Hzmax的信号不能准确复现，所以主要对［0.1，1］m-1空间频率范围内的信号复现进行研究。

对复现路面不平度进行功率谱密度分析，所得路面位移功率谱密度如图9 所示，在空间频率n 在［0.1，1］m-1区间范围内功率谱密度要大于标准功率谱密度。对空间频率n 在［0.1，1］m-1区间范围内功率谱密度大于标准功率谱密度的原因进行分析，主要是由于运动平台没有搭载驾驶座舱，在无负载条件下进行路面谱仿真实验。电动缸的活塞杆带动上平台运动时引起了运动平台底座的振动，加速度传感器在采集数据时也采集到了该频段内运动平台底座的振动信号，为了得到真实的路谱复现数据，需要消除运动平台底座产生的噪声。

图9 上平台复现位移功率谱（未修正）Fig.9 Reproducing displacement power spectrum of the upper platform（uncorrected）

对运动平台底座进行加速度数据的采集并对数据进行处理，得到的位移功率谱如图10 所示。

图10 底座复现位移功率谱（未修正）Fig.10 Reproducing displacement power spectrum of pedestal（uncorrected）

将空间频率n［0.1，1］m-1平均分为9 个区间，对图10 密度谱中相应9 个区间分别用最小二乘法做直线拟合，再用图9 密度谱与所拟合直线作差，得到下页图11 所示功率谱，并与标准路面不平度系数作比较，由图11 可知，去噪后的位移功率谱在几何平均值上下波动且在上下限之间。

图11 运动平台上平台复现位移功率谱（修正后）Fig.11 Reproducing the power spectrum of the displacement of the platform on the motion platform（after correction）

对复现位移功率谱和去噪后的复现位移功率谱与标准位移功率谱做相关性分析，分析它们与标准位移功率谱相关密切程度。

由表4 可以看出，去噪前后功率谱与标准功率谱都有显著的相关性，但是去噪前的复现位移功率谱与标准功率谱的相关性系数仅为0.502，滤噪后的复现位移功率谱与标准功率谱的相关性系数达到了0.816。

表4 相关性分析Table 4 Correlation analysis

由于在计算功率谱时会丢失信号的相位信息，所以并不能从功率谱密度恢复出原始的时域信号，但是可以在已知功率谱的情况下用随机数产生满足该功率谱的信号，并且有无数个。用随机数产生的信号虽然与原始信号不完全相同，但它与原始信号的统计特性相同，在Matlab 中用随机数产生满足图11（a）功率谱的齐次多项式信号，计算得到它的位移均方根值为7.32×10-3m，与标准B 级路面相比误差为3.81%。

表5 A～D 级路面位移均方根误差分析Table 5 Root mean square error analysis of grade A-D road surface displacement

由以上分析可知，B 级路面去噪后位移功率谱与标准功率谱有显著的相关性，相关性系数达到了0.816，并且与标准路面位移的均方根值相比，位移均方根值误差为3.81%，经过去噪后的A～D 级复现路面谱与标准路面谱最大误差不超过5%，说明在消除了运动平台底座的噪声干扰后得到的路面随机扰动的统计特性与真实道路基本一致，运动平台搭载驾驶座舱后，可以实现对真实道路较高逼真度的仿真，同时验证了Stewart 六自由度运动平台对路面谱仿真的正确性。

6 结论

本文针对当前车辆驾驶模拟器对路面振动仿真逼真度不足和缺乏训练沉浸感的问题展开研究，围绕增强驾驶训练模拟器仿真逼真度，提升训练效果的需求，通过研究常见的A～D 级路面，基于谐波叠加法对A～D 级路面进行时频分析建模，实现了Stewart 六自由度运动平台对路面不平度仿真结果进行模拟复现，通过验证，基于该方法复现路面位移功率谱与标准路面位移功率谱有显著相关性，并且复现路面位移均方根值最大误差不超过5%，能够准确复现A～D 级路面。