适用于中小跨径桥梁频率识别的移动检测车辆参数研究

孔烜 ，李思琪 ，2，韩振勇 ，殷鹏程 ，罗奎 ，王秀艳

（1.湖南大学 土木工程学院，湖南 长沙 410082；2.中铁第四勘察设计院集团有限公司，湖北 武汉 430063；3.天津城建设计院有限公司，天津 300122；4.中国建筑第六工程局有限公司，天津 300171）

传统的桥梁模态识别方法大多是通过在桥梁特定部位安装传感器获取桥梁的振动响应信号，再通过信号处理技术来识别桥梁的固有频率、振型和阻尼比等模态参数［1-2］，该类方法可统称直接法.虽然直接法在实际工程中得到了广泛的应用，但由于具有成本高、安装困难、测点单一等缺点［3-4］，其难以满足我国体量庞大的桥梁检测需求.

近年来，出现了通过在车辆上安装传感器获取车辆过桥响应进而识别桥梁模态参数和损伤的方法，即间接法.Yang 等［4］在2004 年首次提出利用移动车辆响应信号获取桥梁固有频率的方法，推导了车辆过桥时的竖向振动响应解析解，通过理论和数值模拟分析、讨论了该方法的可行性.随后，通过一座简支梁桥的现场试验验证了间接法识别桥梁基频的适用性［5］.相比于传统方法，该方法无须在桥梁上布置任何传感器，可以大大提高检测效率.此后，国内外学者针对基于车辆响应的桥梁模态识别开展了大量的研究工作.Shirzad 等［6］利用逆滤波技术对采集的车辆振动响应进行处理，抑制与车辆相关的频率，提取了实验室桥梁模型的基频［7］.Sadeghi等［8］通过对车辆频响函数进行反卷积，并结合二阶盲辨识方法从采集的多源振动信号中提取桥梁振动响应.结果表明，该方法可有效消除车辆悬架系统和路面粗糙度对桥梁频率识别结果的影响.

利用间接法进行桥梁频率识别时，车辆速度、质量和频率等参数对桥梁频率的识别精度和准确性均会产生较大的影响.Lin 等［5］利用“拖车-挂车”移动检测车辆进行现场试验时发现，当移动检测车辆速度小于40 km/h 时可准确识别桥梁的基频，且路面不平整度对桥梁频率识别结果的不利影响随车速的增大而增大.随后，通过改进的检测车辆成功识别了桥梁的高阶频率［9］，并利用桥梁的整体模态振型和局部模态振型进行桥梁的损伤识别［10］.Cantero 等［11］通过实验室试验发现桥梁频率的识别精度不仅与车辆质量有关，还与车辆和桥梁的频率比有关，当车-桥频率比接近1 时桥梁频率偏移较大.Yang 等［12］通过理论分析和数值模拟发现当车辆自振频率与桥梁基频之比大于1 时，频谱图中桥梁的固有频率峰值更加突出，并通过现场试验研究发现利用带通滤波器变分模态分解法可改善桥梁高阶频率识别的可见度［13］.Wang 等［14］将位移传感器安装在车体内部记录车辆前、后轮上方的竖向位移，利用粒子滤波算法对车辆响应进行处理以消除路面平整度的影响，成功获取了桥梁的基频.目前，间接法研究主要集中在理论方法方面，提出的检测车辆参数固定，仅适用于单一桥梁的检测，难以适用于区域内大规模桥梁群的快速检测.

针对目前基于间接法的桥梁频率识别研究存在适用桥梁类型单一、难以适用于区域内大规模桥梁群快速检测的问题，本文提出了参数可调的移动检测车辆，并通过理论推导、试验验证和参数研究对车辆参数进行优化.首先，通过一个简化的车-桥耦合振动系统，介绍基于车辆响应识别桥梁频率的基本原理，并基于车-桥耦合振动理论推导出“拖车-双挂车”检测车辆时域响应差的解析解；其次，通过数值模拟和一座简支梁桥的现场试验对理论解析解进行验证；最后，利用理论解析解进行参数研究，分析了检测车辆的动力参数、车速以及桥梁参数对间接法识别精度的影响.综合考虑车辆参数与桥梁参数对桥梁频率识别的影响，根据在不同桥梁上的应用效果对检测车辆参数进行优化.本文的研究结论可为基于间接法的桥梁频率识别提供参考.

1 基本原理

在车-桥耦合振动系统中，车辆的振动响应包含桥梁振动、车辆自身振动、车辆驱动频率以及桥面不平整度等信息，这使得从车辆振动响应中提取桥梁的动力特性参数变得非常困难.为了消除这些因素的影响，作者提出了一种“拖车-双挂车”车辆模型［15］和车辆响应时域差值法进行桥梁频率识别［16］.在“拖车-双挂车”模型中，前面的拖车主要用于激励桥梁的振动并牵引后面的两辆挂车在桥上移动，如图1所示.车辆之间由连接件进行连接，后面的两辆挂车主要用于获取桥梁的振动响应，相当于移动传感器的功能，其结构如图 2 所示，主要由连接件、连接臂杠、加速度传感器、信号采集器、配重块、车悬架、车轮组成.下面通过一个简化的车-桥耦合振动系统来阐述该方法的基本原理，如图3 所示，T1和T2分别代表两挂车经过桥面上同一位置时的不同时刻.

图1 车辆和桥梁模型示意图Fig.1 Schematic diagram of the vehicle and bridge models

图2 挂车结构详细示意图［15］Fig.2 Configuration of trailer structure［15］

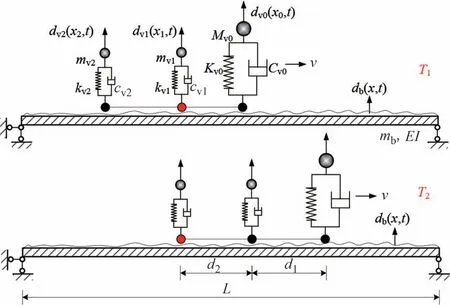
图3 理论模型Fig.3 Theoretical model

1.1 基本假定

在理论推导过程中做如下基本假定：

1）挂车主要功能是采集振动信号，其结构尽量简单，因此采用单自由度车辆模型进行模拟.

2）假定两挂车的车辆参数（质量、刚度和阻尼）完全一致，且挂车质量取较小值，使其对桥梁的激振作用可以忽略不计.

3）仅考虑挂车在桥梁振动和桥面不平整度作用下的竖向振动.

4）忽略车辆的结构阻尼影响.

5）桥梁采用等截面的欧拉-伯努利简支梁.

1.2 理论推导

桥梁计算跨径为L，单位长度质量为-mb，检测车辆匀速行驶通过简支梁桥.拖车-双挂车和桥梁的动力方程，如式（1）～式（4）所示.

式中：Mv0、Cv0和Kv0分别为拖车的质量、阻尼和弹簧刚度；下标v1和v2表示前后两辆挂车和Cb分别为桥梁的线质量、抗弯刚度和结构阻尼；dv0、dv1和dv2分别为拖车v0、挂车v1和挂车v2的竖向位移；假定车辆以匀速v行驶，x0=v⋅t、x1=v⋅t-d1和x2=v⋅t-d1-d2分别为拖车v0、挂车v1和挂车v2与桥梁左端的距离；d1为拖车与第1 台挂车间的距离，d2为两挂车间的距离；db为桥梁的竖向位移；r为桥面不平整度，假设r（x）为一阶可导；δ（x）为狄拉克函数.对以上公式进行求解可以得到桥梁的位移响应，如式（5）所示.

将式（4）代入式（2）可以得到挂车v1的位移响应，如式（6）所示：

同理，可以得到挂车v2的位移响应.在T1时刻和T2时刻，第一辆挂车和第二辆挂车分别经过桥面上同一位置，即T2-T1=d2/v.由于两挂车经过桥面同一位置时存在时间差，为消除路面不平整度的影响，在第二辆挂车中引入一个时间偏移量得到第二辆挂车的位移响应dv2(t+d2/v)，两辆挂车位移响应相减得到在时域内两挂车的位移响应差值，如式（7）所示.

从式（7）中可以看出，通过引入时间偏移量可以将桥面不平整度的影响项消除，有利于更好地从车辆响应中提取桥梁模态信息.

对式（7）进行两次求导得到其加速度响应差，如式（8）所示.对其进行快速傅里叶变换（Fast Fourier Transform，FFT），即可得到包含桥梁频率的频谱图.

2 解析解的验证

为了验证上述推导的解析解，将其与有限元结果和实桥试验结果进行对比.

2.1 有限元验证

基于自主开发的车-桥耦合振动程序［18］对上述推导的解析解进行验证.车-桥耦合单元运动方程矩阵如式（9）所示.

整个车-桥耦合系统的运动矩阵方程如式（10）所示.

利用Newmark-β法对式（10）进行求解，在每一个时间步Δt内，整个车-桥耦合系统的运动矩阵方程可以写成等效线性方程，如式（11）所示.

车-桥耦合系统的动力分析流程如图4所示.

图4 车-桥耦合动力分析流程图Fig.4 Flow chart of vehicle-bridge coupling dynamic analysis

数值验证所采用的混凝土简支梁的基本参数为：弹性模量E=32 GPa，密度D=2.5×103kg/m3，计算跨径L=30 m，矩形截面宽1.2 m、高2 m，将桥梁离散为120 个单元，并基于功率谱密度（PSD）函数的反傅里叶变换对路面不平整度进行模拟［18］.检测车辆中挂车参数为mv=120 kg、cv=1×103N•s/m、kv=6×104N/m，自振频率为 3.56 Hz.拖车与第一辆挂车的间距为d1=0.5 m，两挂车间距为d2=0.5 m.假设检测车辆以10 m/s 的速度匀速通过桥梁.图5（a）曲线表示根据本文推导的解析解，即公式（8）计算得到两挂车的竖向加速度时程响应差，再经FFT 处理得到的频谱曲线.图5（b）曲线表示由车-桥耦合程序（VBI）计算出的挂车响应得到的频谱图.车速的影响使桥梁频率出现了偏移，在频谱图中体现为在桥梁频率处出现2 个接近的峰值，可通过对双峰对应的频率值取平均的方式消除偏移的影响.从图 5可以看出，两种方法识别出的桥梁前3阶频率吻合较好，前3阶桥梁频率识别相对误差分别为0.82%、3.28%和5.08%.结果表明，所推导的解析解可以用于基于间接法的简支梁固有频率识别.

2.2 实桥试验验证

为了进一步验证本文方法的正确性，选取湖南省内一座实桥为研究对象进行试验验证，利用直接法和间接法对实桥的振动频率进行识别.桥梁为6跨预应力钢筋混凝土空心板简支梁桥，总长为 3 m+6×20 m+3 m=126 m，桥宽 5.5 m，选取其中一跨进行试验，如图6所示.

图6 实桥照片Fig.6 Field bridge

采用直接法测量时，将加速度传感器布置在简支梁跨中的桥面上.利用间接法测量桥梁的振动频率时，将加速度传感器安装在移动检测车辆后备箱的轮胎上方位置，如图7 所示.直接法和间接法均采用VibraTest 280（VT280）便携式动态数据采集仪采集数据，采样频率为512 Hz.本次试验采取多次重复性试验来降低误差，首先使检测车辆匀速通过桥梁，并记录车辆通过桥梁时的振动响应信号，记为第1组试验数据.然后，将检测车辆在适当位置调转行驶方向，重新启动，并以同样的速度v匀速通过桥梁，记录车辆通过桥梁时自身的竖向加速度响应.车身完全通过桥梁之后停止采集数据，并对数据进行保存，此为第2组数据.最后，重复上述步骤，一共采集6组车辆加速度响应数据.对所采集到的6 组数据均进行FFT 变换得到包含桥梁频率的车辆加速度响应频谱图.由于噪声和路面不平整度对应的频率有较大的随机性，而车辆振动频率与桥梁频率是固定的，因此，对比多张频谱图即可筛选出桥梁频率.

图7 检测车辆传感器布置Fig.7 Sensor layout on test vehicle

采集到的桥面振动加速度时程响应，以及通过FFT 变换得到的频谱图，如图8 所示.从频谱图中可以得到该桥的前3 阶竖向振动频率，即7.69 Hz、19.54 Hz、30.11 Hz.

图8 桥面振动加速度信息Fig.8 Responses by accelerometer on bridge deck

通过移动检测车辆上的加速度传感器采集到的车辆振动响应时程，以及通过FFT 变换得到的频谱图，如图9 所示.从频谱图中可以粗略地提取该桥的前3 阶竖向振动频率，即7.72 Hz、17.67 Hz 和 31.67 Hz.此外，还识别出检测车辆频率为2.19 Hz.

图9 车辆过桥的振动响应信息Fig.9 Responses collected by the vehicle crossing the bridge

由于没有“拖车-双挂车”样车，无法通过实测数据验证.在此，将实桥的参数代入上述的理论公式，计算得到挂车的加速度信号，再经过FFT 变换得到频谱图，如图 10 所示.其中，图10（a）为对挂车1 响应进行分析处理的结果；图 10（b）为对两挂车响应的差值进行分析处理的结果，即式（8）.

图10 基于解析解的车辆响应Fig.10 Theoretical solution of vehicle dynamic response

表1 桥梁频率识别结果比较Tab.1 Comparision Bridge natural frequencies identified results by different methods Hz

为验证本文理论解析解的正确性和适用性，将直接法的测量结果、移动车辆实测结果和本文理论解析解的结果进行了对比，对比结果如表 1 所示.从表 1 可看出，基于移动车辆实测的实桥前3 阶自振频率与直接法测量结果吻合较好，最大相对误差为9.57%.此外，通过挂车1 的理论解析解响应识别的实桥前3 阶自振频率与直接法的相对误差在0.78%以内，而利用两挂车响应差的理论解析解识别的实桥前3 阶自振频率与直接法的相对误差在0.05%以内.结果表明，利用两辆挂车的响应差识别的桥梁频率精度高于利用单辆挂车响应识别的精度，说明利用两挂车响应差可以有效地消除桥面不平整度的影响，具有很好的应用前景.因此，在第3节和第4节的参数分析中均基于两辆挂车响应差展开研究.

3 车辆参数分析

采用间接法进行桥梁频率识别时，移动检测车辆的质量和刚度对桥梁频率识别影响较大，而识别结果的优劣将会直接影响对桥梁健康状态的评估.面对数量众多、桥型各异的中小跨径桥梁，根据桥梁结构自身特性选择合适的车辆参数变得尤为关键.为了有效评估桥梁频率在频谱图中的可见性，引入可见度指数（Visibility Index，VI）［17］对频谱图中桥梁频率的可辨识度进行评价，其定义式如（12）所示.

式中：VI（ωi）为桥梁频率ωi的可见度指数；A（ωi）为频谱中第i个桥梁频率ωi处的对数振幅；A（ω）为范围内频率ω处的对数振幅；ω1=0.8ωi，ω2=1.2ωi；n为该范围内的频率数.根据其定义可知，可见度指数VI反映了桥梁频率处振幅与该频率附近平均振幅的比值，VI值越大，表示越容易将桥梁频率从频谱图中区分出来.

3.1 车辆频率的影响

通过调整挂车自身质量和刚度来改变其自振频率［15］，在实际中可通过改变车辆配重或车辆悬架弹簧刚度进行调整.本节考虑了不同挂车质量和挂车刚度的6 种工况，如表 2 所示.分别计算表 2 中6 种工况下桥梁前3 阶频率可见度指数，即VI1、VI2、VI3.桥梁为2.1节所用桥梁模型，结果如图11 所示.

表2 挂车频率Tab.2 Trailer frequency

图11 不同车辆频率下的可见度指数Fig.11 Visibility index at different vehicle frequencies

从图11 中可以看出，当移动检测车辆频率分别取1.09 Hz、11.19 Hz 和 35.5 Hz 时，桥梁前3 阶固有频率的VI 取得极大值.为了进一步研究桥梁频率ωb可见度指数随车辆频率ωv的变化规律，以表3 中的极大值点选取3 个不同的车辆频率范围做进一步的精细化分析.ωvrang1～ωvrang3的取值如表3 所示，分别计算桥梁前3 阶频率可见度指数VI1～VI3，结果如图12 所示.

表3 挂车频率Tab.3 The frequency of trailer Hz

表4 挂车参数Tab.4 Trailer parameters

图12 不同车辆频率下的可见度指数（细化）Fig.12 Visibility index at different vehicle frequencies（elaboration）

从图12（a）可以看出，当车辆频率与桥梁第一阶频率比ωv/ωb1=0.5时，桥梁基频的VI1取得极大值，而VI2和VI3在ωvrang1范围内取不到极大值.从图 12（b）可以看出，当车辆频率与桥梁第二阶频率比ωv/ωb2=0.8（或1.2）时，VI2取得极大值，VI1和VI3远远小于VI2.从图 12（c）可以看出，当车辆频率与桥梁第三阶频率比ωv/ωb3=0.9（或1.2）时，VI3取得极大值，VI1和VI2远远小于VI3.结果表明，当挂车自振频率略小于或略大于桥梁第i阶自振频率时，即避免车辆与桥梁的共振现象，对于桥梁的第i阶频率识别效果会更突出，由此可见合理地选择挂车参数有利于提高桥梁自振频率的识别精度.

3.2 车速的影响

进行间接法理论推导时，从检测车辆响应中提取的与桥梁频率相关项L1、L2和Sj均包含车辆速度V，通过这3 项可以看出桥梁频率的提取与速度密切相关.为了分析车速对桥梁频率识别结果的影响，将车速在1～20 m/s 之间进行等间距取值，检测车辆与桥梁均为2.1节所用模型，不同车速下桥梁自振频率的识别结果如图13所示.

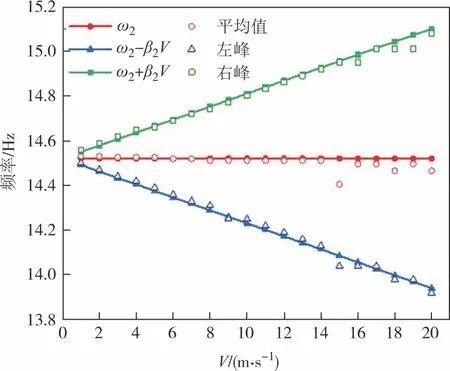
图13 不同车辆速度下识别结果Fig.13 Results of different speeds

从图13 可看出，桥梁频率左右峰值与真实值的偏差随车速的增加而增大，而利用峰值的平均值对桥梁频率的估计都较为准确.当车速小于15 m/s时，误差在1%以内.为了更加具体地分析车速对识别结果的影响，将不同车速下的桥梁频谱振幅、可见度指数和桥梁频率的相对误差进行了比较，如图14所示.

图14 车速的影响Fig.14 Influence of vehicle speed

从图 14（a）和（b）可看出，当V=3 m/s 时，桥梁第1 阶频率的振幅与可见度指数取到最大值.当V=11 m/s时，桥梁第2阶频率的振幅与可见度指数取到最大值.桥梁第3 阶频率的振幅与可见度指数没有明显特征，这可能与高阶频率在拾取信号中占比较低有关.当V<5 m/s 时，前3 阶相对误差均在1%以内，识别精度较高.结果表明，在利用间接法进行桥梁模态识别时，建议移动检测车辆的车速不宜取太高，一般认为V<5 m/s较为合适.

3.3 优化案例

以2.2节简支梁桥作为研究对象，根据前面的分析结果对检测车辆参数进行相应的调整，具体如表 4所示，将检测车辆参数优化前后桥梁的频谱图进行了比较，如图 15 所示.

根据式（12）计算得到优化前的桥梁前3 阶可见度指数分别为0.16、0.002、0.001，优化后的桥梁前3阶可见度指数分别为0.17、0.16、0.12.从图15 可以看出，将检测车辆进行参数优化后得到的频谱图峰值比未优化时更加突出，更有利于桥梁模态参数的准确识别.

图15 优化前后对比Fig.15 Comparison before and after optimization

4 桥梁参数

桥梁自身质量分布、刚度和截面特性等属性均会对桥梁振动特性产生不同程度的影响［19］.根据《公路桥涵设计通用规范》（JTG D60—2015）和2010 年版《公路桥梁结构上部构造系列通用设计图》，本节选取不同的桥梁截面惯性矩I、截面面积A和桥梁跨度L，如表5 所示.桥梁选取4×3×9=108 种不同组合，每种组合可对应多种桥型，用来模拟大范围区域内最具有代表性的、数量最广的桥梁群，表5 中对应的桥梁基频变化范围为0.65～37.17 Hz.主要对108 种工况下的桥梁基频可见度指数进行分析并找出其变化规律.选取11 种不同参数的挂车，其频率分别为1.84、2.52、3.56、4.51、5.38、6.37、7.11、8.51、9.60、10.61和11.62 Hz.

表5 桥梁关键参数Tab.5 Key parameters of bridge

4.1 截面面积的影响

桥梁结构在材料相对固定的情况下，其单位体积的质量主要受截面面积的影响，对11 辆挂车下108座桥梁基频VI进行了分析，并对4种不同截面惯性矩下的结果取平均，结果如图16所示.

图16 不同桥梁截面面积下的VI1平均值Fig.16 VI1 average under different bridge cross section areas

从图16 可以看出，9 种不同跨度下，桥梁基频平均可见度指数VI 整体上随截面面积A的增大而减小，即A=6 m2时可见度指数最大，A=8 m2时可见度指数最小.当跨度为15 m 时，桥梁基频平均可见度指数VI 最高.结果表明，当桥梁跨度相同时，桥梁截面面积越大，越应注意检测车辆参数的选取，以提高桥梁自振频率的识别精度.

4.2 截面惯性矩的影响

桥梁整体的抗弯刚度直接受截面惯性矩的影响，截面惯性矩依次取表5 中参数.对11 辆挂车下108座桥梁基频的VI进行分析，并对3种不同截面面积下的结果取平均，结果如图17所示.

图17 不同桥梁截面惯性矩下的VI1平均值Fig.17 VI1 average under different bridge inertia moments of section

从图 17 可以看出，9个不同跨度下，桥梁频率平均VI 随截面惯性矩I的增大而增大，即当I=3.5 m4时可见度指数最大，I=0.5 m4时可见度指数最小.当跨度为15 m 时，桥梁基频平均可见度指数VI 最高.结果表明，当桥梁跨度相同时，桥梁截面惯性矩越小，越应注意检测车辆参数的选取，以提高桥梁自振频率的识别精度.

4.3 桥梁跨度的影响

桥梁频率可见度与桥梁跨度之间有着密切的联系.为了研究桥梁跨度对桥梁可见度指数VI 的影响，本节将桥梁跨度依次取表5 中参数.不考虑桥梁截面形式的影响，将11 种不同挂车下不同桥梁跨度对VI1的影响进行了比较，并对12种截面组合下的结果取平均，结果如图18 所示，图中Lmax为取得最大可见度指数时对应的桥梁跨度.

图18 不同桥梁跨度下的可见度指数Fig.18 Visibility index at different bridge spans

如图18 所示，当车辆频率在7～11 Hz 时，L=15 m的桥梁可见度最高.当车辆频率在4～6 Hz时，L=20 m的桥梁可见度最高.由此可见，当桥梁跨度较小时，用自振频率较大的检测车辆装置较为合适；桥梁跨度越大，用自振频率越小的检测装置越合适.由于桥梁频率受桥梁跨度影响较大，跨度越大，其相同阶次的自振频率越小，此时检测车辆自振频率越小检测效果越优.因此，为了获得更高的频率可见度，需根据桥梁自振频率对检测车辆的质量与刚度进行相应的调整.

5 结论

针对目前桥梁模态识别间接法难以适用于区域内大规模桥梁群快速检测的问题，本文提出了一种参数可调的移动检测车辆，并通过理论推导、试验验证和参数研究对车辆参数进行优化.以简支梁为研究对象，通过车-桥耦合振动理论推导了“拖车-双挂车”振动响应的解析解，并利用有限元分析和现场试验实测结果验证了本文解析解的正确性和适用性，同时综合考虑车辆参数与桥梁参数对桥梁频率识别的影响，研究间接法在不同类型桥梁上的应用效果并对检测车辆参数进行优化，得出以下结论：

1）车辆自身振动响应受车辆参数的影响较大，对于桥梁低阶频率，当车桥频率比在0.8～0.9（或1.1～1.2）之间变化时，桥梁频率识别效果较好.

2）在利用间接法进行桥梁模态识别时，建议移动检测车辆的车速不宜取太高，一般认为V<5 m/s较为合适.

3）根据桥梁的截面面积、截面形状和跨度对检测车辆的参数进行合理的选取，可提高基于间接法的桥梁频率识别精度，更有利于桥梁模态参数的准确识别.