基于电脑声卡的TDOA声源定位仿真系统
2023-07-29万若楠孙小广张亦勋刘朝山
万若楠,孙小广,张亦勋,刘朝山
(1. 广州城市理工学院电子信息工程学院,广东 广州 510800;2. 火箭军工程大学,陕西 西安 710025)
1 引言
声源定位是一种典型的被动式目标定位技术,仅需要接收来自定位目标的相关特征参数如声音信号到达麦克风阵列的入射角、时间差就可以完成目标定位,具有极强的隐蔽性。因此,作为典型被动式目标定位、跟踪技术越来越成为新的研究热点,在军事、工业、民用等领域都有广泛应用。如鸣笛抓拍系统[1-3],通过麦克风阵列完成音频采集,运用声源定位技术对鸣笛车辆进行定位,最后运用高清摄像头完成抓拍功能。利用声源定位获取声源信息,可以使得视频会议中的麦克风自动跟踪说话人,获得更加精确的采集语音,实现语音增强[4];可以进一步提高智能机器人的声音定位能力、语音交互能力[5,6]。利用声源定位获取声源信息,可对闯入一些禁区如核电站、军事基地等“黑飞”的四旋翼无人机定向定位以及实施有效拦截[7]。目前主要采用的声源定位算法有三种:基于波束形成(Beam Forming)的定位算法、高分辨率谱估计(high resolution spectral estimation)的定位算法,以及到达时延差(Time Difference of Arrival:TDOA)技术定位算法[8]。Matlab 2020a相控阵系统工具箱提供了对应的算法,其中TDOA定位算法相对较简单,是实际应用最广泛的一种定位方法。
2 TDOA的定向定位模型
在基于TDOA的声源定位场景中,声源s(t),环境中仅存在噪声,麦克风1、2接收到的混合声音信号可以被数学建模为[9]
x1(t)=s(t)+n1(t)
(1)
x2(t)=as(t-τ12)+n2(t)
(2)
其中x1(t)与x2(t)为麦克风接收到的混合声音信号,s(t)为声源信号,a为麦克风2接收到的声音信号的能量相较于阵列中心的衰减系数,τ12为声音信号到达麦克风的传播时间差,n1(t)与n2(t)为均值为0、方差为1的高斯白噪声。声源s(t)与噪声n1(t)、n2(t)相互独立。
2.1 基于GCC-PHAT的时延估计算法
在声源定位系统中,麦克风阵列的每个单元所接收到的目标信号xi(t),(i=1,2,3,4)源于同一个声源,显然,不同通道信号xi(t)之间具有较强的相关性。通过计算每两通道信号之间的相关函数Rx1x2(τ),确定出两通道麦克风接收信号之间的时延[10]。
Rx1x2(τ)=E(x1(t)x2(t-τ))
(3)
将方程(1)、(2)代入方程(3),考虑到声源s(t)与噪声n1(t)、n2(t)互不相关,最后化简为
Rx1x2(τ)=α1α2Rss(τ-τ12)
(4)
由相关函数的性质可知,当两个麦克风之间的时延τ12=τ1-τ2时,Rx1x2(τ)取最大值。为抑制噪声和混响干扰,采用广义互相关-相位变换方法(Generalized Cross Correlation Phase Transformation,GCC-PHAT)。在频域内引入φ12(ω)对互功率谱进行PHAT加权,可锐化Rx1x2(τ)的峰值,提高计算的精度。依据互相关函数和互功率谱的关系
(5)
最后利用傅里叶逆变换,可得广义互相关函数Rx1x2(τ)
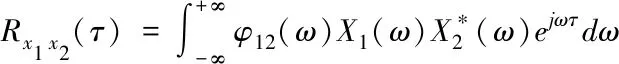
(6)
针对不同的应用环境,可选择不同的加权函数[11,12]。
2.2 空间四元麦克风阵列定位算法
如图1所示,将四元麦克风放置在S1,S2,S3,S4四个点的位置上,组成空间四面体的麦克风阵列,并建立对应的三维直角坐标系。

图1 空间四元麦克风阵列
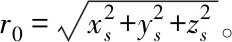
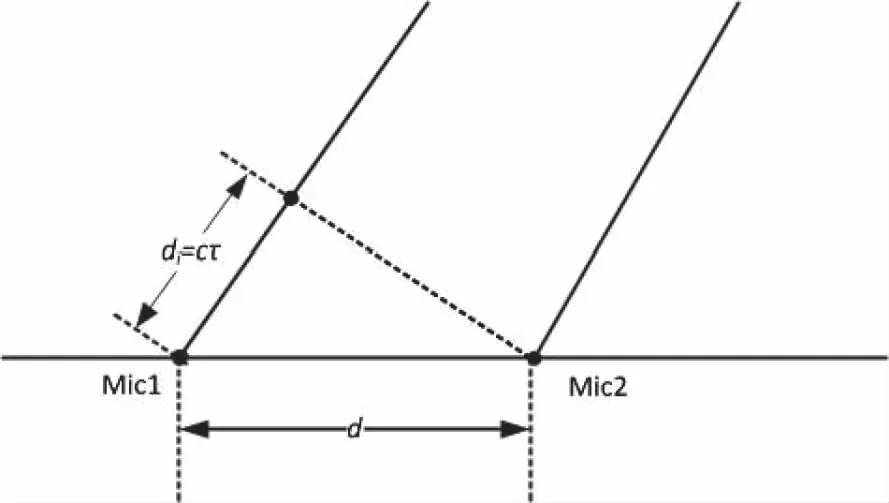
图2 声音信号传播延时与距离关系

(7)
将上述方程组展开,有

(8)
用方程组(8)中的后三个方程分别减去第一个方程,并考虑ri-r1=di1,当di1≪ri时,有ri+r1≈2r0,因此有

(9)
基于方程组(9)可以求得声源点P的位置坐标(xs,ys,zs)与r0和di1关系的表达式

(10)
根据上述声源点的坐标关系,可推导出方位角φ和俯仰角θ
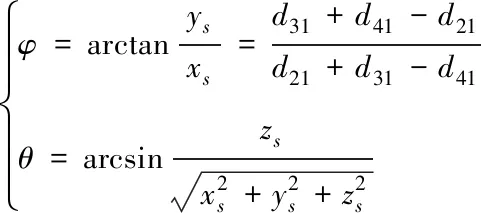
(11)
3 系统硬件设计
系统硬件主要由声波信号采集、处理系统、指向执行系统等组成。
3.1 基于电脑声卡的采样系统设计
在空间直角坐标系中放置四个驻极体麦克风,分别位于四面体的四个顶点上,其中麦克风1(0.14m,0.14m,0.28m)、麦克风2(-0.14m,0.14m,0)、麦克风3(-0.14m,-0.14m,0.28m)、麦克风4(0.14m,-0.14m,0)。声音信号经麦克风采集、信号调理单元放大,放大倍数为100倍左右(可调)。最后,输入电脑声卡,采样频率设为44.1kHz。
由于电脑声卡是双通道,每次只能采集两个麦克风的信号。为降低成本,在采集声音信号时采用继电器控制麦克风的工作,其中麦克风1持续工作,另三个由继电器控制分别依次工作,依据方程组(7),可以测得四麦克风2、3、4与麦克风1之间三组时延,解算出声源的位置。显然,本仿真系统对静止、低速运动声源的定位具有很好的性价比。
3.2 声源跟踪单元
为了控制两轴自由度平台转动,采用ULN2803来驱动28BYJ48型的5V步进电机,达到精确控制角度的目的。控制信号通过驱动芯片与光耦连接,可以隔离掉电机的起止电流对于单片机的影响,从而提高系统稳定性。
4 系统软件设计
为了提高效率、更好控制硬件设备,采用MATLAB软件进行了原理性仿真验证。具体仿真流程见图3。
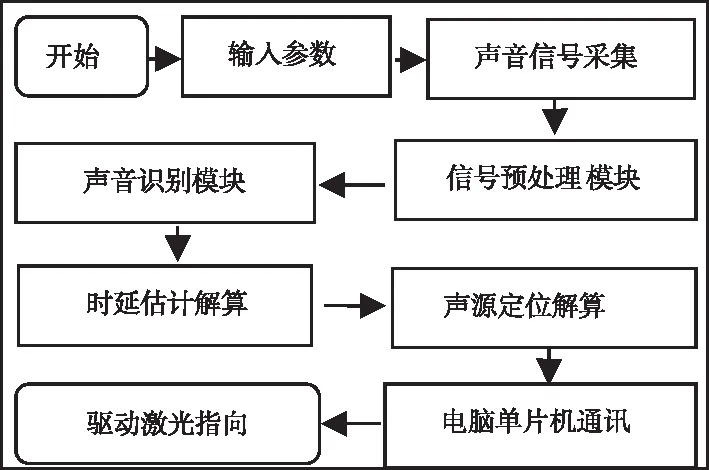
图3 程序流程图
4.1 信号预处理模块
由于采集到的信号具有噪声,因此需要进行过滤步骤。采用MATLAB中的smooth平滑函数和带通滤波器可以实现对声音信号的滤波。
4.2 敏感声音识别模块
倒谱参数(Mel Frequency Cepstral Coefficents:MFCCs)是一种在自动语音以及说话人识别中使用最为普遍的特征,从Mel标度频率域中提取出来,这种特征具有更好的鲁棒性[14,15]。本文直接采用Matlab 2020a音频工具箱(Audio Toolbox)提供的数据集(Data Set);特征提取(Feature Extraction);分类器训练(Training a Classifier);分类器测试(Testing the Classifier)及其相关的支持函数(Supporting Functions),实现声音信号的识别。
4.3 声源定位算法仿真与分析
考虑到影响定向精度的因素主要有声源点的距离、基阵的尺寸以及时延估计误差等,文章主要从以上几个方面对定向精度进行了分析。
图4是通过MATLAB软件仿真得到的时延估计图,由图中可以看到三个峰值,分别对应了三个时延值,将峰值与程序所设定的数值进行比较,基本是一致的,即仿真系统成功识别出声源信息。

图4 GCC-PHAT时延估计图
图5是声源点分别在x、y、z 三个方向上距离变化时对方位角测量误差的影响,仿真中俯仰角取值为35.3°,方位角取值为45°,声阵臂长定为0.14m,时延估计误差为15μs,仿真取点间隔设置为0.05m。

由图5可见,在4到10m的范围内,三个方向上声源点距离对方位角误差的影响不大,整体误差在±1°左右。声源点在x方向改变距离时,得到方位角误差的平均值和标准差分别为:0.31414和0.19745;声源点在y方向改变距离时,得到方位角误差的平均值和标准差分别为:-0.31934和0.22537;声源点在z方向改变距离时,得到方位角误差的平均值和标准差分别为:-0.00680和0.20864;由这些数据可见,在x方向上改变声源点距离时,测量值与预测值较相符合,y方向上的误差相对大一些,同时方位角对z方向声源点距离改变最为不敏感。
图6为麦克风阵列臂长h对俯仰角测量误差的影响,在仿真计算时俯仰角选取为35.3°,方位角选取为45°,声阵臂长取值为0.14m,仿真取点间隔设置为0.01m。由图6可见,麦克风的阵列臂长h对俯仰角精度的测量有较大影响。当麦克风阵列臂长h在0到0.1m的范围内时,俯仰角的仿真误差比较大接近8°,当麦克风阵列臂长h在0.1到1m的范围内变化时,俯仰角仿真误差明显减小,整体误差在±2°左右。仿真结果进一步表明,当麦克风阵列臂长h超过1m时,俯仰角精度也明显低于0.1到1m时的精度范围。总的来说,适当的麦克风阵列臂长h的取值范围对俯仰角估计精度有明显效果。
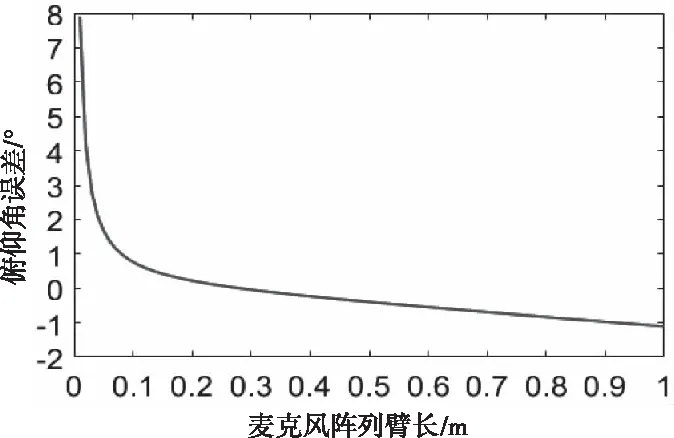
图6 麦克风阵列臂长h对俯仰角误差的影响
5 结论
本文借助MATLAB信号处理工具箱、相控阵系统工具箱,实现有限集合的声音信号识别,并由GCC-PHAT算法确定声波的时延,成功实现了声源定位定向仿真,并分析了对定向精度测量的影响因素,得到了比较理想的结果。本文提供的声源定向定位方法最大优势是实验硬件简单,信号处理、分析算法丰富且易于实现,为开发、评估声源定向定位算法和教学提供了新的仿真平台。
