基于卷积神经网络的长江河口潮位站潮汐频段特征信号快速捕捉方法

樊冯郡，严海勇

(1.浙江省钱塘江管理局勘测设计院，浙江 杭州 310009；2.景宁畲族自治县水利局，浙江 景宁 323500)

0 引言

潮汐是一种受到地球自转影响，在恒星以及天然卫星的作用下，形成的一种以海水等自然界水体为主的周期性变化现象。一般的潮汐仅仅只是一种常见的自然现象，但是某些地区的潮汐已形成自然灾害。在强风暴的作用下，近海地区的海潮会超过警戒水位，摧毁防御措施，形成洪水泛滥的现象，这就是潮灾。在东南沿海地区，台风袭击频率较高，潮灾也较为严重。一旦潮灾来临，不但会造成大额经济损失，还会对当地居民的生命安全造成威胁[1]。为防范潮汐灾害，在加固海堤的同时，还可以对沿海地区的潮汐频段特征信号进行捕捉，以提前获取灾害信息，提醒人们及时防护。一旦灾害范围较大，人们可以提前到其他内陆地区避难，并转移贵重财产，这样就会大幅度降低损失。本文基于卷积神经网络算法，以长江河口潮位站为例，设计了一种潮汐频段特征信号快速捕捉方法。

1 基于卷积神经网络算法的潮汐频段信号特征提取

信号提取是一种较为抽象的提取方法，本文使用卷积神经网络算法，对其进行特征信号进行提取。在神经网络的神经元内，存在权重和偏量参数，由于其具备可重复性，每一个神经元都可以接收一部分数据，并快速运算，这样就可以使得神经网络的最后一层使用单个向量进行变换[2-3]。简单的神经网络由单一结构组成，其主要通过微函数将数据从第一层依次向下传递，直至进入最后一层位置。在这些网络结构中，最核心的类型为3种，分别是卷积层、池化层和全连接层。在卷积层中，一般会存在一组可学习的滤波器，每一个滤波器的频率都很小，但是其深度之间存在较大差别。在输入体积宽度与高度之后，会生成一个二位的映射图，用于空间位置的响应。图像的神经元之间存在一个局部区域的连接结构，在这种不对称下，空间连接在深度上始终是完整的。池化层则是一个会被定期插入到连续卷积层中的空间位置，在减少网络参数与计算量的同时，会不断环节拟合特征，并对池化层中的深度进行独立调整。结合最大值运算等方式，向下操作，得到深度切片的滤波器。在全连接层中，所有网络的神经元均会与上一层的神经元完成对接，并在反向传播中实现参数的更新。由此，可以构建潮汐频段的三角函数：

(1)

式中，h(t)—潮汐分量的累加函数；Wm、Qm—待估算的第m个潮汐群落；Pm、Km—波群理论下的潮汐观测值[4]。通过上述构建的三角函数，可以得到其最优频段估计，并以此计算潮汐频段。通过该方法，可以使用线性表达式获取漂移函数：

fn=2fn-1-fn-2+hn

(2)

式中，fn—仪器的漂移值；fn-1、fn-2—相邻多项式内的漂移表达式；hn—白噪声序列参数。通过上述公式，对其进行特征提取，可以得到观测序列：

(3)

式中，h0—任意可选择的潮汐观测分量；hi—第i个潮汐分量[5]。

2 设计潮汐频段特征信号快速捕捉算法

综合上文中对潮汐频段的信号特征提取方法，可以设计一种潮汐特征信号的快速捕捉算法，算法流程如图1所示。

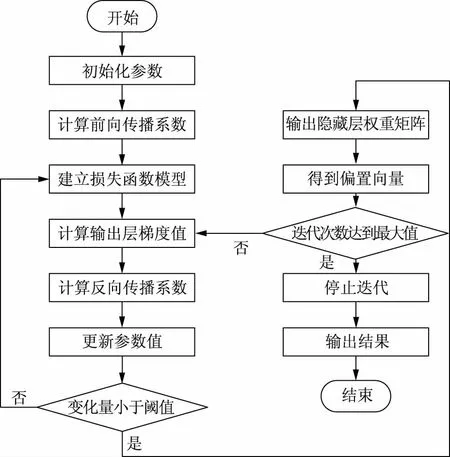
图1 算法流程

由图1可知，首先需要初始化参数，计算前向传播系数。前向传播是一种计算每一层状态与激活值的方法，结合网络参数的损失函数获取优化梯度，并更新参数以获取最小化的损失函数值，通常使用损失函数获取样本真实值。

d(t)=WTy(t-1)+b(t)

(4)

y(t)=λs(h(t))

(5)

式中，d(t)—第t层的神经元状态；y(t-1)—t-1层神经元的前向输出值；y(t)—前向传播系数；λs—激活函数值；h(t)—神经元输出值[6]。同时建立损失函数模型：

(6)

式中，D(WT，bi)—损失函数，WT—权重矩阵；bi—第i层的神经元状态；yi—训练样本的真实值。

据此计算反向传播系数，并同步更新参数值。当变化量大于阈值时，需要返回到损失函数模型建立的步骤，当变化量小于阈值时，需要进一步输出隐藏层权重矩阵，并得到偏置向量。判断迭代次数是否达到最大值，当迭代次数没有达到最大值时，需要重新返回到计算输出层梯度值的阶段，若达到最大值，则可以停止迭代，并得到输出结果，此时即可以对潮汐频段特征信号进行快速捕捉。

3 实验研究

3.1 实例概况

选择瑞安市作为本次实验的工程实例，瑞安市东临大海，所在区域经常遭受台风暴潮的袭击，沿海海塘损毁频繁，又因为中心城区地势较低，导致保护区内经济损失惨重。1949—2016年，瑞安市内发生较大潮灾8次，潮位甚至达到4.37m，严重时全市的海塘和江堤全线失守，土堤几乎夷于平地，海水涌进陆地5km，各乡镇泥质海塘、江堤全线被冲垮，全市直接经济损失高达45亿元。随着城市的发展，受到潮难灾害时所经受的经济损失越来越多，因此需要一种针对潮汐频段特征信号的捕捉技术，以提前得知潮汐灾害，避免人身伤亡或者大额经济损失。

3.2 潮汐信号捕捉与分析

为测试本文设计的基于卷积神经网络的长江河口潮位站潮汐频段特征信号的快速捕捉方法的有效性，对信号检测进行仿真。为评估算法的性能，设定采样率为2.1%，使用高斯随机的采样方式，对数据分段进行压缩，其压缩比为0.01。潮汐信号的采样时间为1h，其中共包括5536个数据点。基于调和分析的方法，获取输出采样数据，在经过预处理以及大气校正之后，可以得到台站的漂移项。由于数据的表现呈现出明显的线性变化趋势，为研究复杂的飘逸特性，可以尝试进行温度校正。在实际的潮位站潮汐频段特征信号采集过程中，由于重力仪器的干扰，温度、大气压均会与重力仪器的零件发生相对位移，因此飘逸效果存在多样性的影响。此时得到的信号特征会与原始数据存在偏差，对数据的处理造成较大干扰。由于海边的温度变化较为快速和频繁，很多重力仪器的部件还会发生热胀冷缩现象，其相对受力点也会发生变化。对日内潮汐频段信号进行采集，每隔1h，提取一次潮汐频段信号，在卷积神经网络下的特征信号提取结果如图2所示。

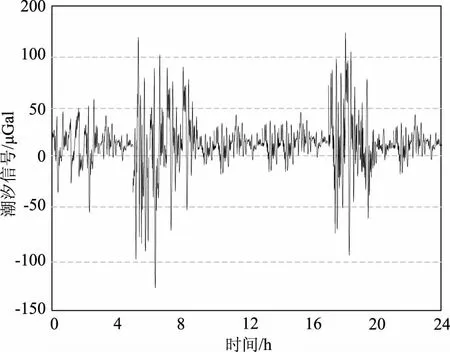
图2 潮汐频段特征信号

由2可知，在24h的潮汐频段特征信号捕捉提取过程中，信号分量的变化非常明显，其变化范围见表1。

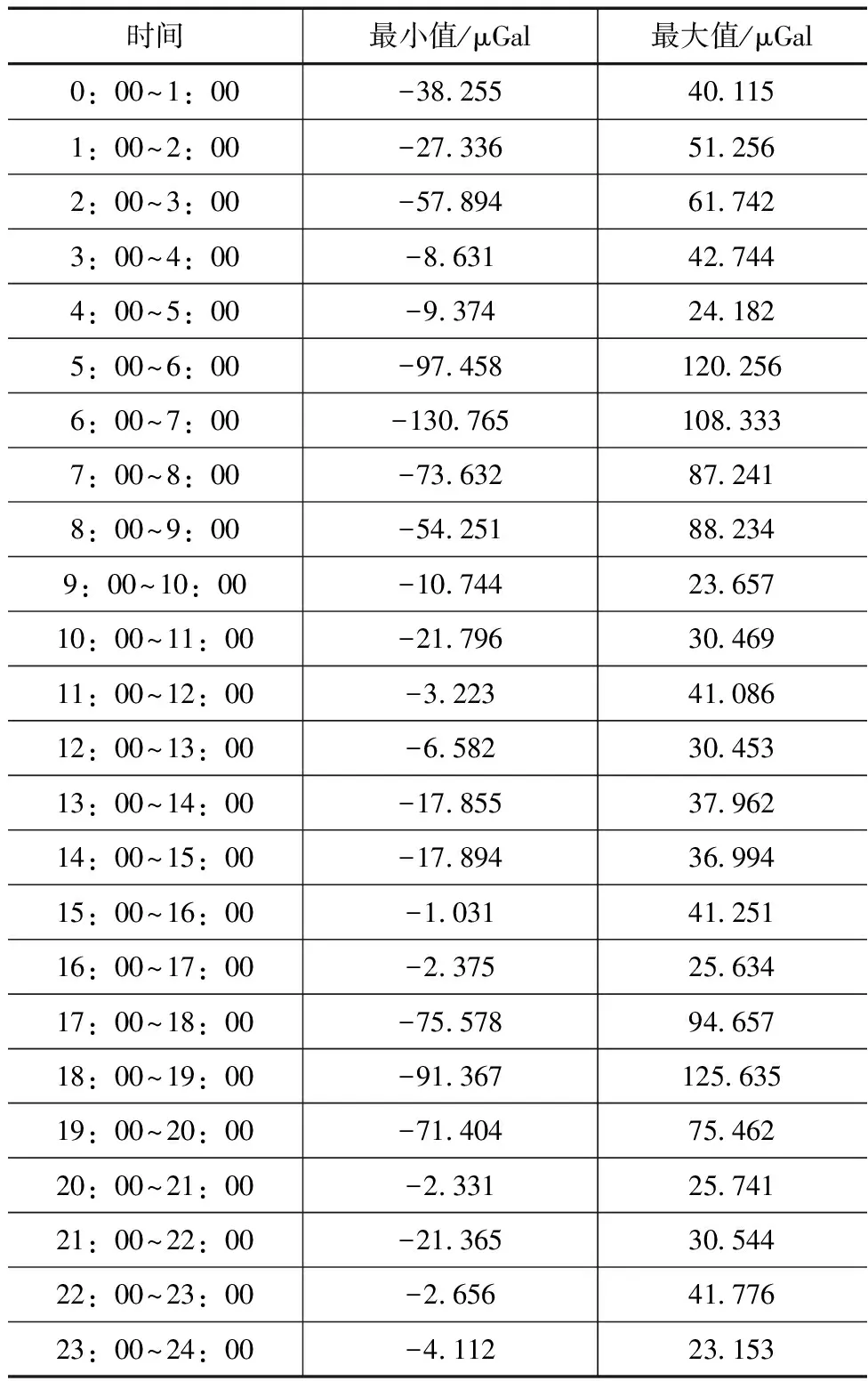
表1 潮汐分量变化范围

统计24h内所有潮汐频段的特征信号，其中9∶00～17∶00时间段的信号变化幅度最小，其信号频率的最小值仅有-22，最大值则为42。在5∶00～9∶00以及17∶00～20∶00这2个时间段内的信号变化幅度最大，最小值可以达到-131，最大值则为126。这2个变化较大的时段正好是温度变化最剧烈的频段，此时仪器零件发生位移，信号特征与原始数据存在偏差，因此潮汐频段变化剧烈。由此可见，本文设计的基于卷积神经网络的长江河口潮位站潮汐频段特征信号的快速捕捉方法精度较高，可以准确地得到信号结果。

4 结语

潮汐是一种常见的自然现象，但在强风暴的作用下，近海地区的海潮会超过警戒水位，进而出现潮灾现象。对此，本文设计了一种于卷积神经网络的长江河口潮位站潮汐频段特征信号的快速捕捉方法，该信号捕捉方法可以对海边的潮汐信号进行提取与分析，实验结果表明，进行潮汐频段特征信号捕捉的过程中，信号分量的变化非常明显，说明本文方法的精度较高，具有实用性。但在进行潮汐频段特征信号快速捕捉计算的过程中，由于算法较为复杂，导致计算时间没有达到预期效果，在接下来的研究中，将对算法进行改进，旨在缩短运算时间，进一步提高信号捕捉效率。