基于模糊滑模观测器的永磁同步电机无位置控制

许元威

（广东工业大学，广东 广州）

引言

PMSM 要实现闭环控制，就必须在其转子轴上加装一台旋转变压器或机械传感器，通过此种方式，在PMSM 运行过程中，将转子的位置信号、转速信号一并列入闭环控制过程中，通过此种方式，保证PMSM 的闭环控制达到预期效果。但在转子轴上加装一台机械传感器，会导致电机体积较大、造价较高、工作环境受限、可靠性较低，从而制约PMSM 的应用范围[1]。为克服加载机械传感器所存在的缺陷，研究人员们提出了一种无位置的控制方式，其实施过程是通过对电机端电压和电流信号的处理，并根据信号中所包含的电气信号，提取电机速度和转子位置信息，以此为依据进行PMSM 闭环控制，从而达到对电机高精度无位置控制的目的[2]。

1 永磁同步电机建模

永磁同步电动机是一类与常规电动机不同的同步电动机，此类电机不采用励磁绕组的设计方式，而是采用永久磁铁。按照永磁体布置方式的不同，可将电机划分为两种：一种是隐极电机磁体，另一种是凸极电机磁体。下述将以凸极式PMSM 为研究对象，对其展开建模研究[3]。建模前，对凸极式PMSM 的结构进行分析，见图1。

图1 凸极式PMSM 的结构

为实现对与之方面工作的简化，可假设凸极式PMSM 在结构中属于理想电机，在运行过程中，凸极式PMSM 需要满足以下三个方面的条件：忽略或排除铁芯中定子饱和对其的影响；忽略或排除铁芯中存在的磁滞损耗与涡流损耗；可假定凸极式PMSM 中的三相电流均属于理想条件下的正弦波电流[4]。

在排除外界因素对凸极式PMSM 运行的影响后，可在三相电流理想条件下，建立电机数学模型，建模中，对其中的三相电压进行描述，见公式（1）：

式中：uA、uB、uC代表凸极式PMSM 三相电压；Rs代表电机在运行过程中存在的磁滞损耗；iA、iB、iC代表凸极式PMSM 三相电流；ψA、ψB、ψC代表凸极式PMSM三相磁链。在此基础上，进行 ψA、ψB、ψC三相磁链方程的表述，如公式（2）所示：

式中：L 代表三相磁链长度；f 代表磁链自感应值。经过坐标转换，可以进行上述公式的推导，经过推导后得到在相对静止坐标系下，进行电机转矩方程描述，将电机转矩方程作为永磁同步电机模型，如公式（3）所示：

式中：Te代表凸极式PMSM 的电机转矩方程；pn代表电机电角频率。通过上述方式，完成永磁同步电机建模研究。

2 基于模糊滑模观测器的无位置传感器控制

针对上述构建的永磁同步电机模型，现有控制方法是将MTPA 与负直轴弱磁相结合。但这种控制方法在无位置传感器控制工况下，无法确保转子角度不会出现误差。因此，针对这一问题，为了确保控制方法的应用稳定性，提出一种对角度误差具有较强容错能力的控制方法[5]。利用基于静止坐标系下转矩观测电压相角控制，谐波恒转矩曲线不会随着角度误差的产生而出现偏移，从而避免出现电压限制椭圆不相交的问题产生。在这一过程中，弱磁区的电压始终处于饱和状态，而在dp 坐标系当中，可以通过下述公式实现对电压的具体描述：

式中：Vd代表d 轴上的电压值；Vq代表q 轴上的电压值；Vsmax代表最大电压值；δ代表电压矢量与q 轴形成的夹角。图2 为电压矢量。

图2 电压矢量

在弱磁区中，电压处于饱和状态，此时输出的转矩调节与电压相位有关。在低速区域内，电压幅值可以进行自由调节，可选用双电流闭环控制策略，用以实现对电流的准确控制和快速响应。随着转速的不断提升，电压幅值逐渐达到饱和状态。在这一时刻，需要切换电压相位角的控制方式，通过转矩闭环，实现对电压相角的调节，从而实现更准确的转矩输出[6]。同时，在这一过程中需要时刻关注控制精度是否受到了角度误差的影响。同时，控制时需要避免参数变化对于电机转矩造成的影响。在对反馈转矩时无法按照上述方式进行的情况，需要在静置坐标系当中完成对转矩的计算。转矩的观测可依据下述公式：

式中：T 代表转矩观测值，即弱磁区稳态转矩；p 代表定子电阻；φα和 φβ代表静止坐标当中的磁链；iβ和iα代表与静置坐标链条磁链相对应的定子电流。上述方案对发电势积分具备结构简单的优势，可以降低计算难度[7]。但是由于纯积分的应用会造成一定初值误差的累计以及直流偏置问题产生，进而影响到观测效果。针对这一问题，为了能够更加准确的计算出转矩输出结果，需要对上述磁链计算进行改进。在控制过程中设置一个阀值 λ ，λ的取值范围在0.1～0.5之间，λ的取值越大，则说明直流分量的抑制效果越理想，但是暂态响应越慢。在此次研究当中，将 λ的取值设置为1/3。

3 控制策略切换

在控制过程中，实现MTPA 控制与电压相角控制的平稳切换，必须满足下述两个条件：第一，切换的过程中时机必须正确；第二，在切换的前后需要确保电压指令的连续性[8]。通常情况下，只有下述情况才需要切换控制策略。首先，在使用MTPA 控制方法时，只有转速提升或转矩指令提升时，才需要切换控制策略。其次，在弱磁控制的过程中，只有转速降低或转矩指令为上升时，才需要进行对控制策略的切换。图3 为切换控制策略时的电机工作点变化。

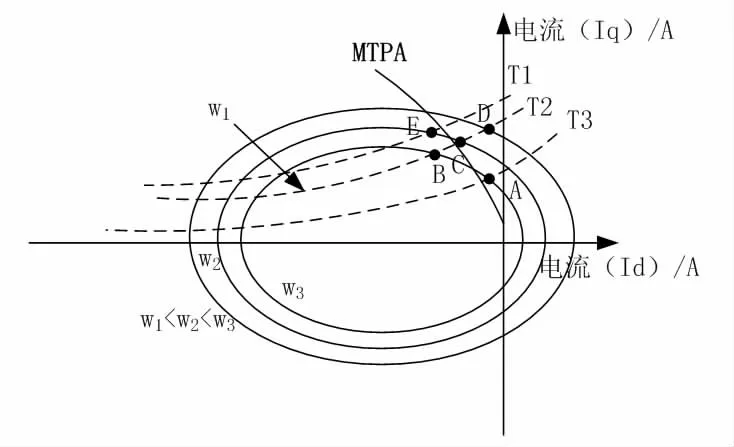
图3 切换控制策略时的电机工作点变化示意

从双电流环控制转变为电压相角控制弱磁时，为了能够保证电机控制的性能，需要将切换点设置在电压饱和的周围。除此之外，为了能够使电流环性能稳定，需要预留一定的电压裕度，因此其切换条件为：

式中：Vs代表逆变器输出电压；Udc代表直流侧电压。通过上述公式描述可以得出，在控制过程中，逆变器输出电压为直流侧电压的0.6 倍时，采用双闭环的电压相位控制方式，在未到达最大输出电压的情况下进行弱磁控制，在提前进入弱磁区时，对永磁同步电机的效率进行一定程度的牺牲，但同时也避免了因电机参数不准确而导致的电流环无法控制的问题，增强控制方法的稳定性。

当转速达到图3 所示的w2时，此时电压限制椭圆与MTPA 曲线相交于一点，该点为C 点。在确保转速不发生改变的情况下，此时达到了MTPA 算法输出转矩的最大限制（图3 中T2 所示）。为了进一步提升转矩输出，并达到T1 转矩，需要将控制策略切换为电压相角控制。此时，运行点逐渐从C 点移动到了E 点。在保持转矩不发生改变的情况下，为了进一步提升转速，使其达到w3，需要切换控制策略为电压相角控制。此时，运行点逐渐从C 点移动到B 点。

从电压相角控制切换到双MTPA 控制时，其基本原理为：保持w3转速，并在T2 转矩下，电压相角控制运行在B 点位置。在不考虑切换控制策略时，当电机转动速度不发生改变时，输出转矩会逐渐下降到T3，此时电机运行位置从B 点移动到了A 点。当转矩不发生改变，转速逐渐下降到w1时，此时电机运行的点位逐渐从B 点转移到了D 点。在这两种情况下，运动点的移动过程穿过了MTPA 曲线。在切换的过程中，当d轴电流与MTPA 指令重叠后，此时控制策略从电压相角控制切换为MTPA 控制。

4 仿真检验

为检验控制技术的应用效果，使用Simulink/Matlab，在实验中进行控制技术的仿真。在使用本文技术控制电机的基础上，引进传统的观测器，进行电机无位置控制，本次传统控制采用PI 控制方式，控制前，进行电机相关参数的设定，具体参数见表1。

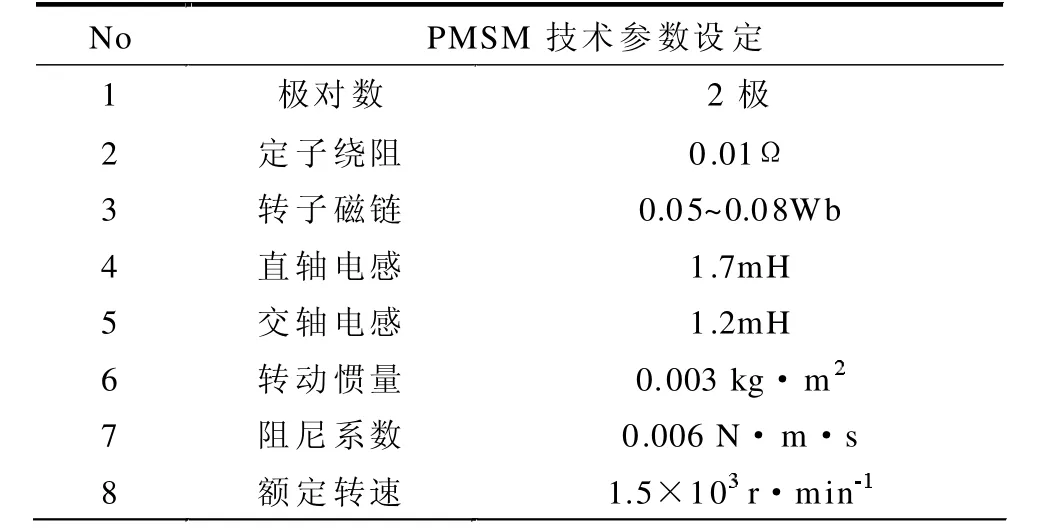
表1 PMSM 技术参数设定

完成电机参数的设计后，按照规范，使用本文此次设计的控制技术与传统控制技术，进行电机无位置控制，对比控制技术应用后电机转速误差，见图4。

图4 控制技术应用后的电机转速误差

图4 中上图代表应用本文控制技术后的电机转速误差；图4 中下图代表应用传统控制技术后的电机转速误差。

5 结论

根据图4 所示的控制结果可以看出，在排除外界条件干扰的条件下，使用本文设计的技术进行电机转速控制，控制后电机转速最大控制误差在20 r·min-1～-30 r·min-1范围内，而使用传统控制技术进行电机转速控制，控制后电机转速最大控制误差>200 r·min-1。由此可以证明，在对比传统方法的控制效果后，本文设计的控制方法可以更好地实现对电机转速误差的控制，通过此种方式，排除相关因素对永磁同步电机运行过程的影响，提高电机运行过程的安全性、可靠性与稳定性。

目前，与本文研究相关的内容在科研领域内仍处于初步探索阶段，相关研究成果仍不完善。希望通过此次的研究，为科研等工作的实施予以帮助。同时，也可以在后续的工作中，选择更多的指标作为对照指标，从更多的角度，深入相关工作的讨论中，以深化本次研究成果，通过研究更直观的掌握本文方法在具体应用中的优势与不足，为查缺补漏提供技术层面指导。