低速冲击下负泊松比蝴蝶形蜂窝夹芯板的动力响应*
2023-07-27余阳,付涛
余 阳,付 涛
(昆明理工大学机电工程学院,云南 昆明 650500)
负泊松比超材料结构具有良好的应力扩散性能、极高的剪切模量和能量吸收能力[1]。因此,具有负泊松比特性的蜂窝胞元结构组成的蜂窝夹芯板受到了广泛关注。与传统均质板结构相比,蜂窝夹芯板具有轻质、高强度和优异的抗冲击能力等特点,主要应用于航空航天和高速铁路等领域[2-3]。但在实际应用中,石子或者冰雹等物体的撞击会对蜂窝夹芯板造成损伤,这些损伤将直接影响蜂窝夹芯板的强度和刚度,进而影响结构整体的稳定性[4-5]。因此,建立能够准确分析低速冲击下蜂窝夹芯板动力响应的模型是有必要的,可以为蜂窝夹芯板的结构设计和制造提供帮助。
关于夹芯板在低速冲击下的动力响应,学者们已开展了丰富的研究。蔺晓红等[6]采用ABAQUS 有限元分析软件,对碳纤维增强铝合金板(carbon reinforced aluminum laminates,CARAL)受低速冲击时的动力响应及损伤进行了数值模拟。谢素超等[7]通过低速落锤实验和包含面板、胶层及蜂窝的细节数值模拟,探究了铝蜂窝夹芯板在低速冲击下的动力响应及损伤模式。Zhang 等[8]通过实验和数值模拟,研究了铝蜂窝夹芯板在低速冲击下的动力压缩性能和能量吸收能力。Liu 等[9]采用ANSYS 数值模拟方法,研究了铝蜂窝夹层结构的冲击位移、应力和应变随时间的变化规律。Palomba 等[10]采用低速冲击实验研究了双层蜂窝夹芯板的能量吸收能力。Zhang 等[11]通过单泡沫弹丸冲击带有玻璃层压铝增强环氧树脂(glass laminate aluminum reinforced epoxy,GLARE)的蜂窝夹芯板的实验,研究了前面板金属层和复合层之间的脱粘、纤维断裂、屈曲、剪切和芯部断裂规律。关于蜂窝夹芯板在低速冲击下的动力学响应研究中,上述研究者主要基于实验为主,与数值模拟结果相对比,而对于夹芯板动力学响应的理论研究很少。Hazizan 等[12]使用简单的能量平衡模型对铝蜂窝夹芯结构的冲击响应进行建模,但是该模型更适用于蜂窝夹芯梁的动力响应研究。Zhang 等[13]以金属泡沫芯和纤维-金属层压板(fibre-metal laminate,FML)组成的完全夹持夹层梁为研究对象,通过建立理论模型和数值模拟的方法,研究了具有纤维金属层压板的夹层梁的动态响应。后来,Zhang 等[14]通过数值方法研究了由金属泡沫芯和纤维-金属层压板组成的夹持方形夹层板(square sandwich plates,SSP)的动力响应。Sun 等[15]提出了一种基于哈密顿原理的通用分析建模方法,用于研究具有韧性金属面板的蜂窝夹芯板的低速冲击响应。Wu 等[16]提出了一种改进的高阶剪切变形理论(higher-order shear deformation theories,HSDT),用于分析简单支撑的复合材料和蜂窝夹芯板的自由振动。
当前的研究结果表明,人工负泊松比蜂窝胞元结构能够与多学科交叉融合[17],而且负泊松比蜂窝夹芯板在能量耗散和能量吸收方面比传统六边形蜂窝芯的蜂窝夹芯板更有优势[18]。基于负泊松比蝴蝶形蜂窝夹芯板,关淮桐等[19]研究了蝴蝶形蜂窝夹芯板的振动特性,提升了抑制工程应用中共振发生的能力。
目前,对于蜂窝夹芯板在低速冲击下的动力响应理论模型研究较少,且未涉及蝴蝶形蜂窝夹芯板在低速冲击下的动力响应。因此,本文中,主要以负泊松比蝴蝶形蜂窝夹芯板为研究对象,基于哈密顿原理和一阶剪切变形理论,推导具有负泊松比特性的蝴蝶形蜂窝夹芯板的运动方程,建立两自由度组成的质量-弹簧求解模型,采用Navier 法和Duhamel 积分对蝴蝶形蜂窝夹芯板的运动方程进行解析求解,将Abaqus 有限元数值模拟结果或已发表文献结果与采用本文中所建立的理论模型计算出的结果作对比来验证理论模型的有效性,并利用本文中所建立的理论模型分析蝴蝶形蜂窝夹芯板在低速冲击下的动力响应,讨论不同结构参数对蝴蝶形蜂窝夹芯板在低速冲击下动力响应的影响。
1 蜂窝夹芯板动力响应理论模型
假设蜂窝夹芯板主要是由2 个蒙皮层和1 个夹芯层组成,其中芯层由具有负泊松比特性的蝴蝶(凹入式蜂窝)芯组成。如图1(a)所示,在蜂窝夹芯板的中间平面建立笛卡尔直角坐标系(x,y,z),沿z方向为蜂窝夹芯板的高度,沿x和y方向为蜂窝夹芯板的长度和宽度分别记为Lx和Ly,蜂窝夹芯板的总高度为h,顶部蒙皮层高度为ht,底部蒙皮层高度为hb,夹芯层高度为hc。此外,蜂窝夹芯板受到初始速度为cs,半径为Rs的球形冲击器的冲击载荷。在本文中,量符号上标或下标t 、c、b 和s 分别表示顶部蒙皮层、夹芯层、底部蒙皮层和球形冲击器。负泊松比蝴蝶形蜂窝夹芯层组成的胞元结构如图1(b)所示,Δ、Δ1、Δ2和Δ3为胞元的壁厚,L1、L2和L3为胞元的壁长,α1、α2、β1和β2为胞元壁的倾斜角度,1/4 胞元的长为s,宽为d。为了便于计算和分析,可设L1=L2, α1=α2, β1=β2。
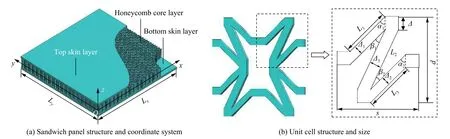
图1 蜂窝夹芯板和胞元结构示意图Fig.1 Structure schematic diagram of the honeycomb sandwich panel and the unit cell
1.1 蜂窝夹芯板的运动方程
为了获得蜂窝夹芯板的位移场,采用一阶剪切变形理论[20]描述蜂窝夹芯板的位移场:
式中:u、v和w分别表示中间平面相对于x、y和z轴的面内横向位移,φx和φy为旋转位移分量,t为时间。
与位移场有关的任意位置的横向应变-位移关系为:
式中:εx、εy为正应变,γxy、γxz和γyz为切应变。
蜂窝夹芯板的线性本构关系可以写成:
式中:上标i=t, c, b。其中刚度系数分别为:
式中:E、G和µ分别为基体材料的弹性模量、剪切模量和泊松比。蝴蝶形蜂窝夹芯层的等效弹性模量、等效剪切模量和等效泊松比公式[21]分别为:
式中:η=α1−β1,e=L3/∆3,R=e(ssinη−dcosη)2+e3(dsinη+scosη)2,η2=d/s,d=2∆+L3cosη,s=3∆+2L1sinα1−L3sinη,k=L1/∆1。
根据哈密顿原理[22],蜂窝夹芯板一阶剪切变形理论运动方程为:
式中:q为冲击载荷,I0、I1和I2为质量惯性矩,Nx、Ny和Nxy为轴向力,Qx和Qy为剪切力,Mx、My和Mxy为力矩。可定义为:
1.2 蜂窝夹芯板的运动方程求解
考虑四边简支条件下蜂窝夹芯板的自由振动:
采用Navier 法[23]求解系统的固有频率,将位移分量表示为双三角级数形式:
式中:α=mπ/Lx,β=mπ/Ly,Umn(t)、Vmn(t)、Wmn(t)、Xmn(t)和Ymn(t)为位移振幅分量,m和n为模数。冲击载荷q可表示为:
系数Qmn(t)为:
将式(8)和(9)代入式(4),并利用Galerkin 法,忽略平面内转动惯量,可得:
根据式(11),可得到一个线性二阶微分方程:
采用Duhamel 积分[24],将式(10)代入式(12),可得Wmn(t)系数为:
式中:ωmn为蜂窝夹芯板的固有频率。
如图2 所示,建立质量-弹簧模型用于求解球形冲击器与蜂窝夹芯板之间的接触力F(t)。在质量-弹簧模型中,p1和p2分别为球形冲击器和蜂窝夹芯板的质量,δ(t)为接触变形位移,w1(t)和w2(t)为2 个质量块在撞击后随时间变化的位移响应,K1和K2为等效接触刚度。

图2 球形冲击器与蜂窝夹芯板接触的等效理论模型Fig.2 An equivalent theoretical model of contact between the spherical impactor and the sandwich panel
接触变形δ(t)的位移为:
根据文献[25],冲击器在冲击期间的非线性赫兹冲击力为:
式中:Es、µs和Et、µt分别为球形冲击器和蜂窝夹芯板顶部蒙皮层的杨氏模量和泊松比。使用等效刚度K1进行解析求解,冲击力可计算为:
等效接触刚度的计算公式为[26]:
式中:Γ(·)为Gamma 函数,δm为最大接触变形。且:
运用牛顿第二运动定律,两自由度质量-弹簧模型的平衡方程为:
式(20)的初始条件为:
由式(14)、(17)、(20)和(21)可以计算出接触力为:
利用式(18)、(13)和(22),可以得到蜂窝夹芯板的横向位移方程:
1.3 理论模型验证
主要从以下3 个方面来验证当前理论模型的有效性。
首先,以负泊松比蝴蝶形蜂窝夹芯板为例,假设蜂窝夹芯板的长度Lx=300 mm,宽度Ly=300 mm,总高度h=12 mm,夹芯层高度hc=10 mm,顶部蒙皮层和底部蒙皮层高度相同,蜂窝胞元壁厚Δ=2 mm,蜂窝胞元壁的倾斜角度β1=β2=45°,α1=α2=60°,蜂窝胞元壁长L1=L2=6 mm,L3=8 mm。假设蒙皮层和夹芯层的材料相同,基体材料的弹性模量E=69 GPa,泊松比µ=0.3,密度ρ=2700 kg/m3。通过Abaqus 软件建立蝴蝶形蜂窝夹芯板,将蜂窝板赋予上述材料参数,在分析步管理器中,选用Lanczos 特征值求解器对蜂窝夹芯板的振动特性进行求解。对于蝴蝶形蜂窝夹芯板的简支边界条件,分别在x=0 和x=Lx边,限制y方向与z方向的位移和绕y轴的旋转;在y=0 和y=Ly边,限制x方向和z方向的位移以及绕x轴的旋转。如图3所示,蝴蝶形蜂窝夹芯板的网格类型为十节点二次四面体网格单元,网格尺寸为5.0 mm。采用相对收敛的方法对当前网格的收敛性进行验证,从表1 中可以看出,蝴蝶形蜂窝夹芯板的一阶固有频率随着网格尺寸的减小而减小,并逐渐趋于一个极限值691.25Hz,其在5%误差下的固有频率为725.81 Hz,因此网格尺寸为5.0 mm 时可以满足网格收敛要求。利用本文所建立的理论模型和有限元数值模拟的方法,蝴蝶形蜂窝夹芯板的前5 阶固有频率如表2 所示,可以看出理论模型结果于数值模拟结果吻合较好,最大的相对误差为6.53%。
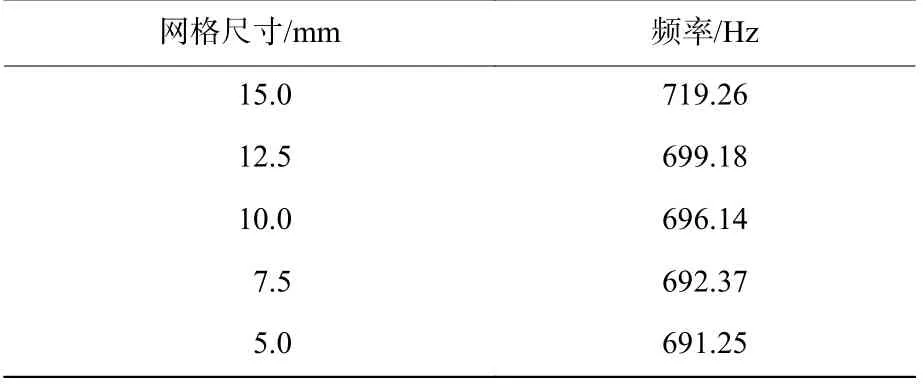
表1 网格尺寸对一阶固有频率计算结果的影响Table 1 Influences of mesh size on the calculated results of the first-order natural frequency

表2 蝴蝶形蜂窝夹芯板的前5 阶固有频率Table 2 The first five order natural frequencies of the butterfly-shaped honeycomb sandwich panel
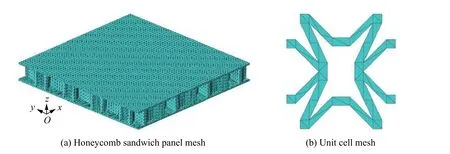
图3 有限元数值建模的网格划分Fig.3 Finite element numerical modeling meshing
其次,通过Abaqus 有限元软件建立蝴蝶形蜂窝夹芯板低速冲击模型,蜂窝夹芯板的几何尺寸和材料参数与上述相同。球形冲击器的半径为10 mm,弹性模量Es=200 GPa,泊松比µs=0.3,密度ρs=7971.8 kg/m3。创建动力显式分析步,对蜂窝夹芯板设置四边简支边界条件,分别在x=0 和x=Lx边,限制y方向与z方向的位移和绕y轴的旋转;在y=0 和y=Ly边,限制x方向与z方向的位移和绕x轴的旋转。如图4所示,采用十节点二次四面体网格单元对蝴蝶形蜂窝夹芯板进行网格划分,其边界网格尺寸为10.0 mm。为了更好地分析蜂窝夹芯板横向位移,将蜂窝夹芯板的中心20 mm×20 mm 区域内的网格尺寸设为1.0 mm。球形冲击器采用相同的网格单元进行网格划分,其网格尺寸为1.0 mm,在球形冲击器底部设计1 个参考点并与蜂窝夹芯板顶部蒙皮层中心点相接触,接触点的坐标为(Lx/2,Ly/2,h/2)。将参考点与球形冲击器进行刚体约束,然后对参考点设置不同的冲击速度(6、8、10、12 m/s)。为了防止低速冲击过程中发生干预穿透问题,选择通用接触,面面接触在法向设置为硬接触,在切向设置为罚函数接触,其摩擦因数为0.2。采用上述相同的方法对当前的网格收敛性进行验证,如表3 所示,当球形冲击器以8 m/s 的速度冲击蜂窝夹芯板时,蜂窝夹芯板中心最大横向位移随着中心区域网格尺寸的减小而增大,并逐渐趋于一个极限值0.2556 mm,在5%的误差范围内,中心网格尺寸为1.0 mm 时可以满足网格收敛要求。采用本文理论模型和有限元数值模拟方法,在不同冲击速度下,蜂窝夹芯板最大中心横向位移变化情况如表4 所示,可以计算出,本文理论模型计算结果与数值模拟结果的最大相对误差为6.84%。

表3 低速冲击下蜂窝夹芯板中心网格尺寸对中心最大横向位移计算结果的影响Table 3 Influence of center grid size on the calculated maximum lateral displacement of the sandwich panel center under low-velocity impact
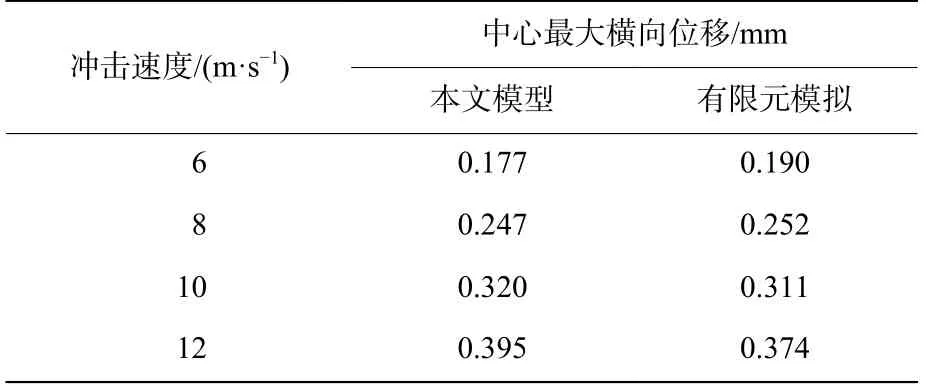
表4 不同冲击速度下蝴蝶形蜂窝夹芯板的横向位移Table 4 Lateral displacement of the butterfly-shaped honeycomb sandwich panel at different impact velocities

图4 蝴蝶形蜂窝夹芯板低速冲击有限元模型Fig.4 The finite element model for the butterfly-shaped honeycomb sandwich panel subjected to low-velocity impact
最后,将本文理论模型计算的接触力与Yang 等[26]和Wu 等[27]计算的接触力进行对比,来验证本文理论模型的有效性。在矩形板与冲击器的材料参数和几何尺寸与文献[26-27]中的保持一致的情况下(见表5),当冲击器以1 m/s 的速度冲击矩形板时,本文理论模型计算的接触力随时间变化曲线与文献[26-27]中的接触力的对比如图5 所示。从图5 可以看出,板结构与球形冲击器之间的接触力总体变化趋势相同,理论模型计算的接触力与文献[26-27]中的接触力最大相对误差为8%。

表5 矩形板和冲击器的材料参数和几何尺寸[26-27]Table 5 Material parameters and geometrical sizes of the homogeneous panel and impactor[26-27]
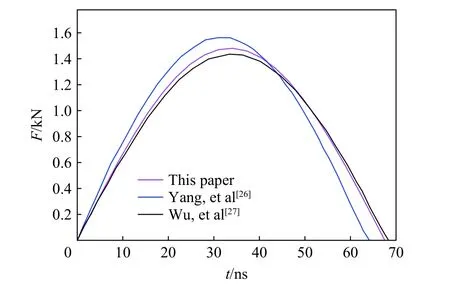
图5 接触力随时间的变化Fig.5 Variation of contact force with time
上述3 种方法对本文中所建立的理论模型进行了有效性验证,理论模型计算与有限元数值模拟所得的蝴蝶形蜂窝夹芯板前5 阶固有频率的最大相对误差为6.53%,中心最大横向位移的最大相对误差为6.84%。理论模型与文献[26-27]计算得到的接触力最大相对误差为8%。结果表明,这3 种方法所求得的结果均在误差可接受范围之内,验证了本文理论模型的有效性。
2 蜂窝夹芯板的参数分析
利用所建立的理论模型来研究蜂窝胞元和夹芯板的几何尺寸对负泊松比蝴蝶形蜂窝夹芯板动力响应的影响。球形冲击器的主要材料参数和几何尺寸见表5,冲击的速度为6 m/s。蜂窝夹芯板的基体材料参数为:E=69 GPa,µ=0.3, ρ=2700 kg/m3;蝴蝶形蜂窝夹芯板的几何尺寸为:Lx=Ly=300 mm,h=12 mm,ht=hb=1 mm;蝴蝶形蜂窝胞元的几何尺寸为:L1=L2=6 mm, β1=β2=45°, α1=α2=60°,L3=8 mm,Δ=2 mm。
2.1 蜂窝胞元几何尺寸对蜂窝夹芯板动力响应的影响
通过改变蜂窝胞元几何尺寸,研究它们对蝴蝶形蜂窝夹芯板动力响应的影响。蜂窝胞元厚度Δ分别设为1 、2 和3 mm,蝴蝶形蜂窝夹芯板的横向位移随时间的变化如图6(a)所示,可以看出,随着蜂窝胞元厚度的增大,蝴蝶形蜂窝夹芯板的横向位移不断减小。这表明,随着蜂窝胞元厚度的增大,蜂窝夹芯板的抗冲击特性在增强。同理,蜂窝胞元角度β1分别设为20°、35°和50°,蝴蝶形蜂窝夹芯板的横向位移随时间的变化曲线如图6(b)所示,可以看出,随着蜂窝胞元角度的增大,蝴蝶形蜂窝夹芯板的横向位移也在不断增大。这表明,蜂窝夹芯板的抗冲击特性随着蜂窝胞元角度的增大而减弱。
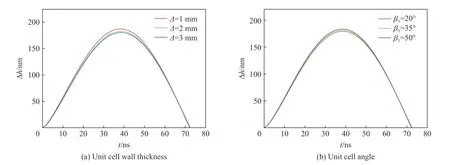
图6 胞元几何尺寸对蝴蝶形蜂窝夹芯板动力响应的影响Fig.6 Influences of the unit cell geometry parameters on dynamic responses of the butterfly-shaped honeycomb sandwich panel
2.2 夹芯层高度对蜂窝夹芯板动力响应的影响
通过改变夹芯层高度,研究它们对蝴蝶形蜂窝夹芯板动力响应的影响。蜂窝夹芯板的顶部蒙皮层和底部蒙皮层的高度均为1 mm,顶部蒙皮层与夹芯层的高度比分别为1∶6、1∶10 和1∶14,蜂窝夹芯板的长度和宽度均为300 mm,球形冲击器的速度为6 m/s。蜂窝夹芯板的基体材料参数为:E=69 GPa,µ=0.3, ρ=2700 kg/m3;蝴蝶形蜂窝胞元的几何尺寸为:L1=L2=6 mm, β1=β2=45°, α1=α2=60°,L3=8 mm,Δ=2 mm。不同的顶部蒙皮层与夹芯层的高度比对蝴蝶形蜂窝夹芯板动力响应的影响如图7 所示,在相同的冲击载荷下,随着蜂窝夹芯板的夹芯层与顶部蒙皮层高度比的增大,蜂窝夹芯板的横向位移减小,表明蜂窝夹芯板的抗冲击特性增强;随着高度比的增大,蜂窝夹芯板与冲击器的接触力也增大,表明蜂窝夹芯板的能量吸收能力增强。在实际的工程应用中,可通过适当增大芯层高度来提高蜂窝夹芯板的抗冲击特性和吸能效果。

图7 顶部蒙皮层与夹芯层的高度比对蝴蝶形蜂窝夹芯板动力响应的影响Fig.7 Influences of the height ratio of the top skin layer to the sandwich layer on dynamic responses of the butterfly-shaped honeycomb sandwich panel
2.3 夹芯长度尺寸对蜂窝夹芯板动力响应的影响
同理,通过改变蜂窝夹芯长度尺寸,研究它们对蜂窝夹芯板动力响应的影响。设蜂窝芯的高度为10 mm,顶部蒙皮层和底部蒙皮层的高度均为1 mm,蜂窝夹芯层的宽度为100 mm,宽度和长度比分别为1∶1、1∶1.5 和1∶2,球形冲击器的冲击速度为6 m/s,蜂窝夹芯板的基体材料参数和蜂窝胞元的几何尺寸与上述相同。不同的宽长比对蜂窝夹芯板动力响应的影响如图8 所示,随着蜂窝夹芯层的长度增大,最大横向位移减小,而蜂窝夹芯板与球形冲击器的接触力在增大,这表明蜂窝夹芯结构的抗冲击能力和能量吸收能力随着蜂窝夹芯板长度的增大而增强。因此,在实际的工程应用领域,适当提高蜂窝夹芯板的长宽比来增强结构的抗冲击能力。
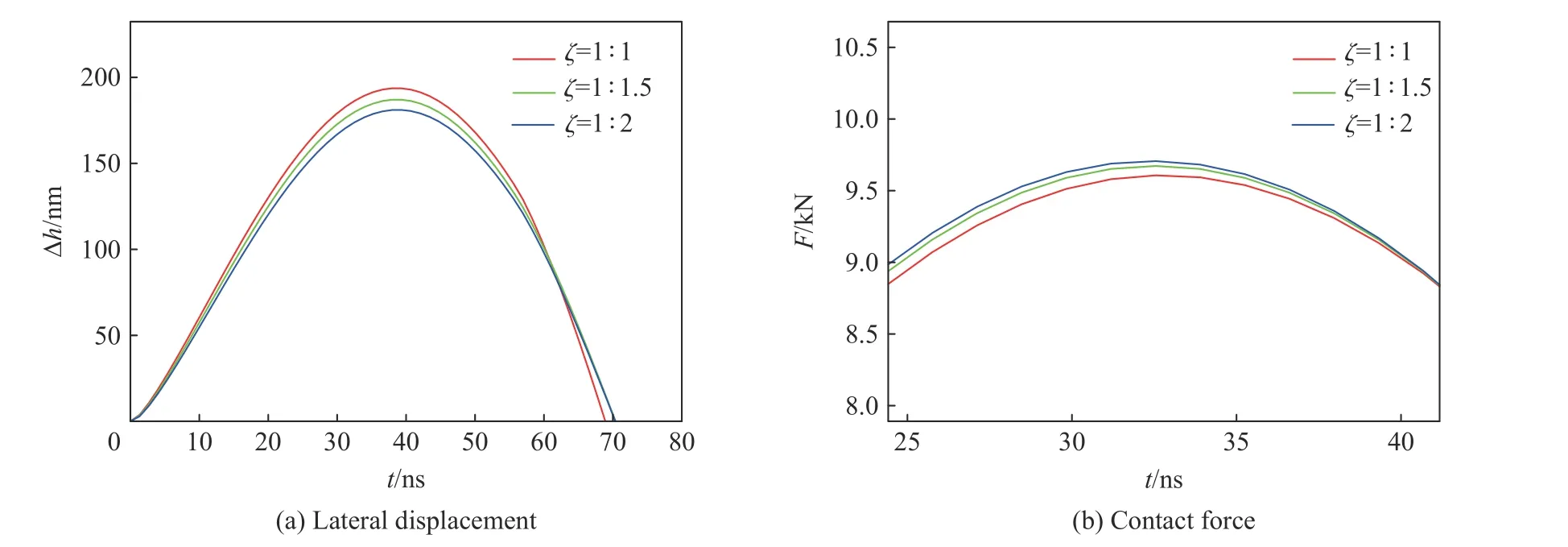
图8 宽长比对蝴蝶形蜂窝夹芯板动力响应的影响Fig.8 Influences of the width-length ratios on dynamic responses of the butterfly-shaped honeycomb sandwich panel
3 结 论
以负泊松比蝴蝶形蜂窝夹芯板为研究对象,探讨了在低速冲击下蜂窝胞元和夹芯板的几何尺寸对夹芯板动力响应的影响,得到以下结论。
(1) 基于一阶剪切变形理论和哈密顿原理建立了蝴蝶形蜂窝夹芯板在低速冲击下的动力响应理论分析模型,并对理论分析模型进行了解析求解。将理论模型计算结果与Abaqus 数值模拟结果或已发表的文献结果进行对比,验证了理论模型的有效性。
(2) 在相同的冲击载荷下,蝴蝶形蜂窝夹芯板的抗冲击特性随着蝴蝶形蜂窝胞元壁厚的增大而增强,随着蜂窝胞元角度的增大而减弱。当蜂窝胞元厚度从1 mm 变化到3 mm 时,蜂窝夹芯板的抗冲击特性提升3.7%。
(3)增大蜂窝夹芯板的夹芯层高度和夹芯板长度,可以提升蜂窝夹芯板的抗冲击特性。当夹芯层高度从6 mm 增大至14 mm 时,蜂窝夹芯板的最大横向位移减小5.4%;当夹芯板长度从100 mm 增大至200 mm 时,蜂窝夹芯板最大横向位移减小6.1%。
需要说明的是,本文中所建立的蜂窝夹芯板动力响应分析模型适用于低速冲击下所产生的弹性形变研究,而对于高速冲击所产生的塑性形变,本文的理论模型还需要进一步的改进和验证。
