抽油杆柱动力屈曲模拟装置液压加载系统设计与性能仿真
2023-07-27李海祥董世民王传锋
李海祥,董世民,王传锋
(燕山大学机械工程学院,河北秦皇岛 066004)
0 前言
有杆抽油系统在我国油田中应用最为广泛,抽油杆柱是有杆抽油系统中非常重要的构件之一,它是否能正常工作直接关系到机械采油的经济效益。当抽油杆柱在直井中做上下往复直线运动时,由于受到油管的约束与外载荷的影响而发生屈曲变形和横向振动,容易产生严重的偏磨问题[1-2]。目前研究表明:井筒内的杆柱屈曲构型取决于杆柱底端集中轴向压力的大小。杆柱的横向振动属于无限自由度系统,再考虑管壁的约束或碰撞,求解其振动微分方程变得十分困难[3-6]。为了能够有效开展抽油杆柱力学性能的研究工作,建立一个液压加载的抽油杆柱的横向振动和动力屈曲的模拟装置,不仅可以验证数学模型仿真结果,还能观察杆柱瞬态屈曲变形和横向振动,对于进一步深入研究抽油杆柱屈曲和横向振动的耦合振动也具有十分重要的意义。本文作者将对模拟装置的液压加载系统进行建模仿真分析,从理论方面验证模拟装置的可行性和可靠性。
1 杆柱动力屈曲模拟装置方案设计
设计一种抽油杆柱动力屈曲模拟装置,总体设计方案如图1所示。根据总体设计方案可知,该装置主要由液压加载部分、杆柱测试部分以及数据采集处理部分构成。

图1 抽油杆柱动力屈曲模拟装置总体方案
液压加载部分提供杆柱试件所受的轴向拉压力,其系统原理如图2所示。杆柱测试部分主要包括杆柱试件、外筒和支撑架,用来模拟抽油杆柱在井筒中受力后的形态变化。数据采集处理部分主要包括PLC、拉压力传感器、位移传感器和扭矩传感器,可以处理返回的信号并检测杆柱试件发生屈曲变形的临界载荷、测量横向振动特性等。

图2 液压加载系统原理
液压加载部分的工作原理如下:液压系统的压力由比例溢流阀调节,通过电磁换向阀的动作控制液压缸的活塞杆伸出或者缩回,从而实现杆柱试件所受轴向载荷的周期性变化;压力传感器采集实际的输出压力进行反馈,PLC系统根据误差进行控制调节,最终达到精准的压力控制目的。模拟装置的压力控制方式如图3所示。此模拟装置的目的在于控制系统加载的拉压力,观察和研究抽油杆柱在底端周期性外载荷作用下的瞬态屈曲和横向振动。

图3 模拟装置压力控制方框图
结合工程实际中抽油杆柱所受的周期性作用力,预先设定加载的压力-时间曲线。如图4所示:Fmax为抽油杆柱所受的最大轴向拉力,Fmin为最大的轴向压力;T为一个完整的加载周期,其中TU代表抽油杆柱的上行程时间段,TD代表抽油杆柱的下行程时间段,TU1和TD1的大小决定了上下行程中的轴向力变化速度。
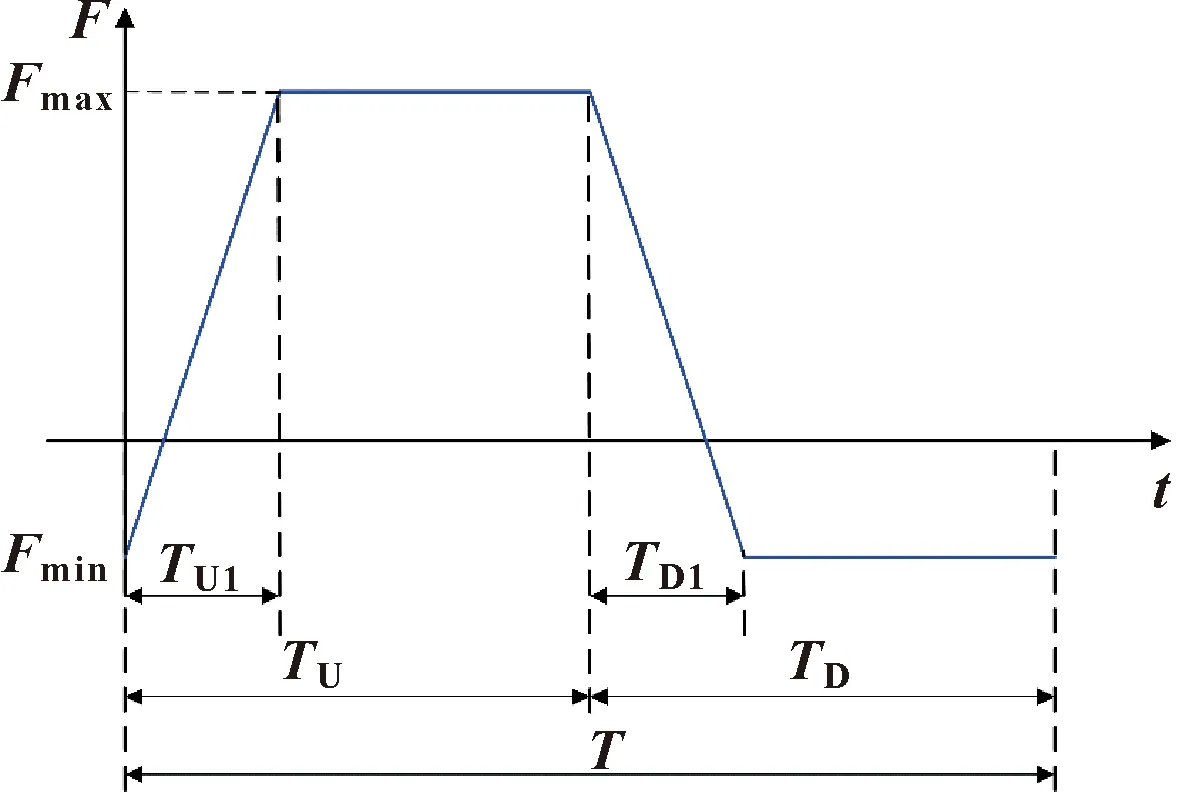
图4 预设的压力-时间曲线
根据油田运行实际经验,抽油杆柱在工作过程中,当轴向压力超过临界值之后抽油杆柱会产生屈曲变形。在作者设计的模拟装置中,液压系统提供杆柱试件所需的轴向力,在某个时刻杆柱试件随轴向压力增大产生的屈曲变形会导致液压缸活塞杆轴向位移量的突变,会使液压缸工作腔内的压力产生波动,影响实验精度。所以文中使用压力闭环控制的加载方式,减小抽油杆柱屈曲变形对压力加载的影响,使实际工作过程更加贴合预设的压力-时间曲线。
2 液压系统建模仿真
为了证明抽油杆柱动力屈曲模拟装置的可行性和可靠性,使用MATLAB软件中的Simulink仿真模块对模拟装置中的液压加载系统进行仿真分析。Simulink仿真模块能够通过搭建图形化模型将己建立的数学模型表达出来,表现方式更加直观清晰。
2.1 比例溢流阀建模仿真
比例溢流阀作为此系统中的核心零部件,首先对其进行仿真分析。此模拟装置因为所需压力、流量较小,所以选定华德DBETR型直动式比例溢流阀。比例放大器作为比例溢流阀的直接控制元器件,可以简化成比例环节。结合文献[7]可知,直动式比例溢流阀数学模型比较复杂,应用起来比较困难。结合实际应用中的经验,本文作者将含比例放大器的直动式比例溢流阀简化成一个典型的三阶系统,传递函数如下所示:
(1)
其中:ω0为衔铁组件和等效弹簧刚度决定的二阶环节的固有频率(rad/s);ωr为由管路的容腔大小决定的一阶环节的转折频率(rad/s);δ0为综合阻尼系数;Kee为比例阀阀芯位移增益(m/V);Kpy为压力-位移增益(Pa/m)。
结合式(1),在Simulink仿真环境中采用阶跃信号作为输入,搭建的比例溢流阀仿真模型如图5所示。

图5 比例溢流阀的Simulink仿真模型
代入比例阀DBETR-10B2.5M样本数据,比例溢流阀在阶跃信号下的压力响应如图6所示。

图6 比例溢流阀的压力响应
结合图6可以看出:比例溢流阀作为调压元件,当控制信号一定时,可以获得稳定的系统压力。此模拟装置通过改变比例溢流阀的控制信号,再联合液压系统中的减压阀,可以实现无级调节系统的压力,使系统能够满足预先设计的压力-时间曲线。
2.2 液压加载系统建模仿真
根据系统的结构和工作条件,可作如下假定:
(1)不考虑液压系统内油路管道内压力损失;
(2)不考虑液压系统中油液温度变化;
(3)液压缸工作腔内各处压力相等。
为使建模仿真更加简单高效,现对液压系统进行简化处理(相较于杆柱的受拉过程,杆柱在受压过程中力学性能变化更加复杂,所以文中取杆柱受压过程为例)。如图7所示,液压系统工作过程中,油液Qs1通过液压泵进入系统,一部分油液Qy1通过比例溢流阀流回油箱,剩余部分油液QL1进入液压缸推动活塞杆对负载元器件进行周期性加载。现对液压系统进行整体的建模仿真分析。
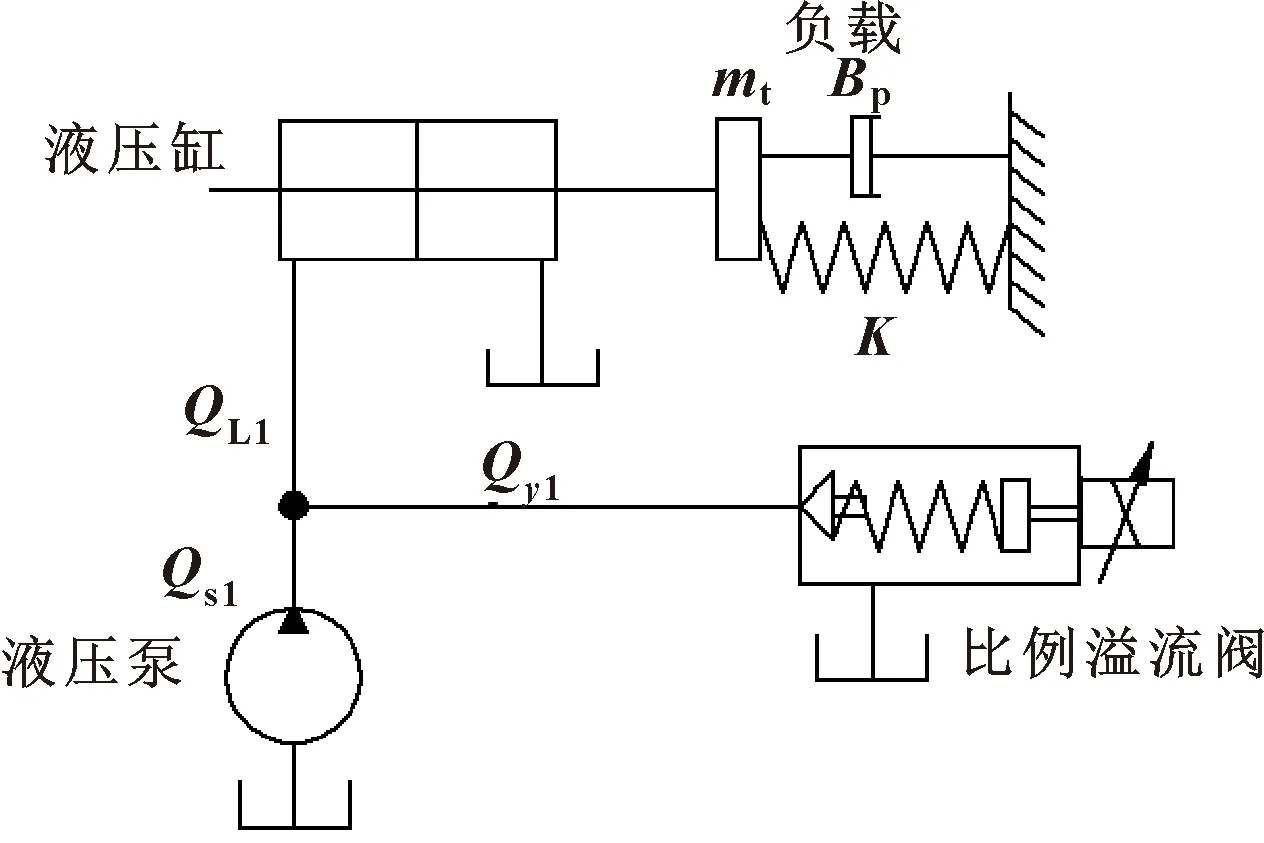
图7 简化的模拟装置液压系统
如图7所示,此模拟装置将测试杆柱简化成弹簧阻尼系统,根据力平衡方程和流量连续方程,结合液压缸的力输出特性,可得:
(1)液压缸柱塞受力平衡方程
(2)
其中:ps1(t)为液压缸工作腔油压力(Pa);A1为液压缸柱塞有效作用面积(m2);mt为活塞和负载折算到活塞上的总质量(kg);Bp为活塞和负载的黏性阻力系数;K为负载的弹簧刚度(N/m);fL为负载力(N)。
(2)柱塞腔的流量连续性方程
(3)
其中:qL1(t)为进油流量(m3/s);ps1(t)为进油压力(Pa);E为油液体积弹性模量(N/m3);V1液压缸进油腔总容积(m3);cL1为液压缸泄漏系数(m3/(N·s));y(t)为活塞位移(m)。
(3)压力传感器方程,一般将其视为比例环节
Uf=kf·Fg(t)
(4)
其中:Fg(t)为液压缸输出力(N);kf为压力传感器增益(V/Pa)。
对式(2)—式(4)在初始条件为零的条件下进行拉氏变换,常数项的拉氏变换为零,可得公式如下:
Ps1(s)A1=(mts2+Bps+K)Y(s)+FL(s)
(5)
(6)
Uf(s)=kf·Fg(s)
(7)
通过上述方程式并结合比例溢流阀的传递函数框图,可得到液压系统的传递函数方框图,如图8所示。

图8 液压系统传递函数框图
从图8可以看出:影响液压系统压力输出的主要因素有电压信号、负载力以及系统的流量。此模拟装置采用定量泵驱动,流量为恒定值,可在忽略负载力变化的情况下研究系统的稳定性。液压系统开环传递函数的仿真模型如图9所示。

图9 系统开环传递函数Simulink仿真模型
文中实验装置中使用3 m长的杆柱试件,材料为ABS工程塑料,杆柱试件直径为25 mm,主要仿真参数如下:负载的弹簧刚度K=44 N/m,活塞和负载折算到活塞上的总质量mt=6 kg,活塞和负载的黏性阻力系数Bp=29 000,液压缸柱塞有效作用面积A1=1.47×10-3m2,液压缸内油液的泄漏系数cL1=3×10-11m3/(N·s),液压缸进油腔的总容积V1=1.47×10-4m3,压力传感器增益kf=4×10-6V/Pa,油液体积弹性模量E=8×108N/m3。
代入数据和比例阀的样本参数后可得系统开环传递函数Bode图,如图10所示。根据Bode判据[8],此实验装置开环系统有正的幅值裕度和正的相位裕度,其闭环系统是稳定的,所以此模拟装置的液压控制系统是稳定的。
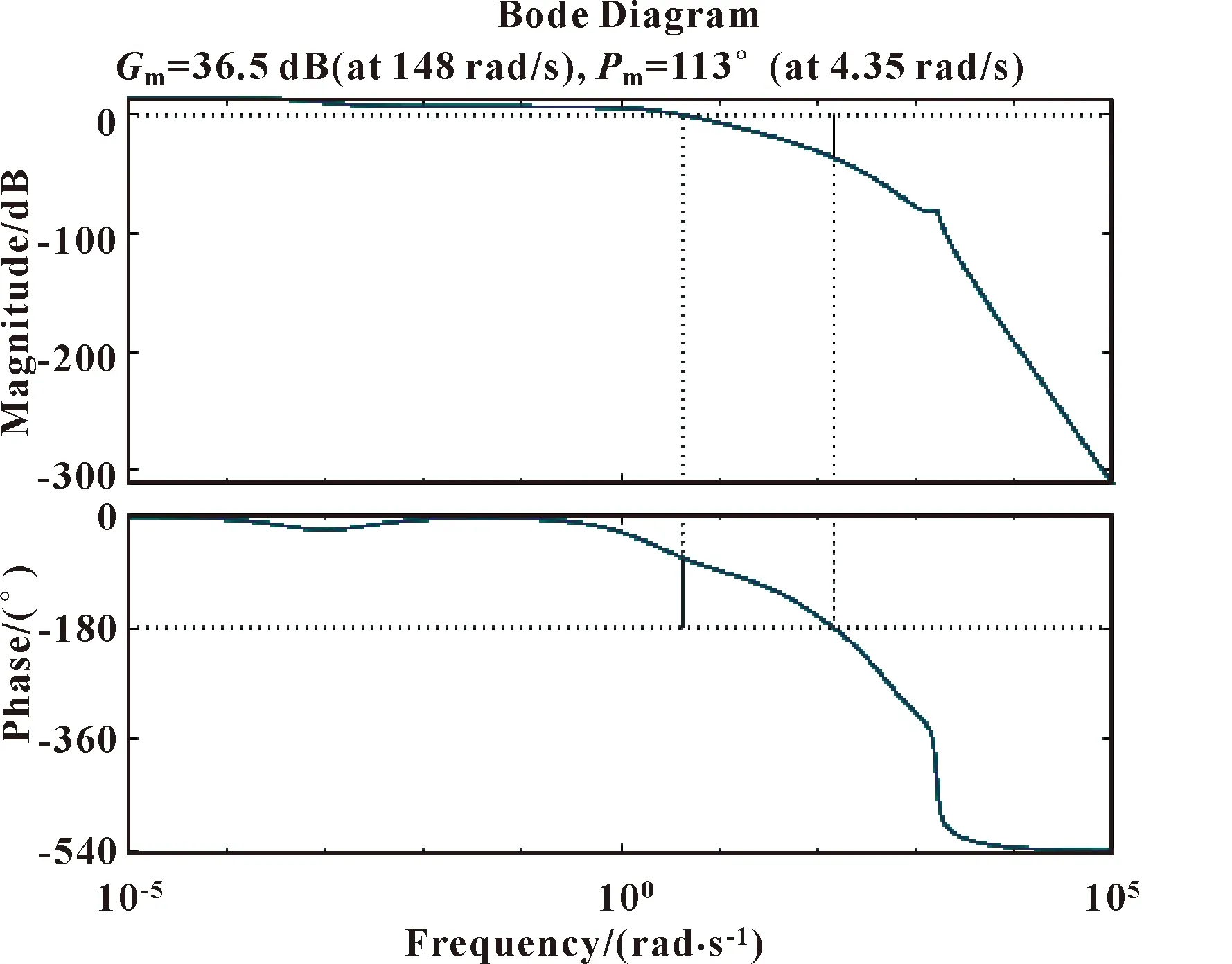
图10 系统开环传递函数Bode图
2.3 交变负载力对液压系统影响的建模仿真
结合井筒内抽油杆柱的力学特性,在拟静力学的条件下,通过差分法离散杆长,求解杆柱横向振动的微分方程后,可以发现随着轴向压力的增大,杆柱在某个瞬间会产生失稳发生屈曲变形。现调整系统框图的结构,观察以负载力为输入的系统压力的响应。系统压力框图和仿真模型分别如图11和图12所示。
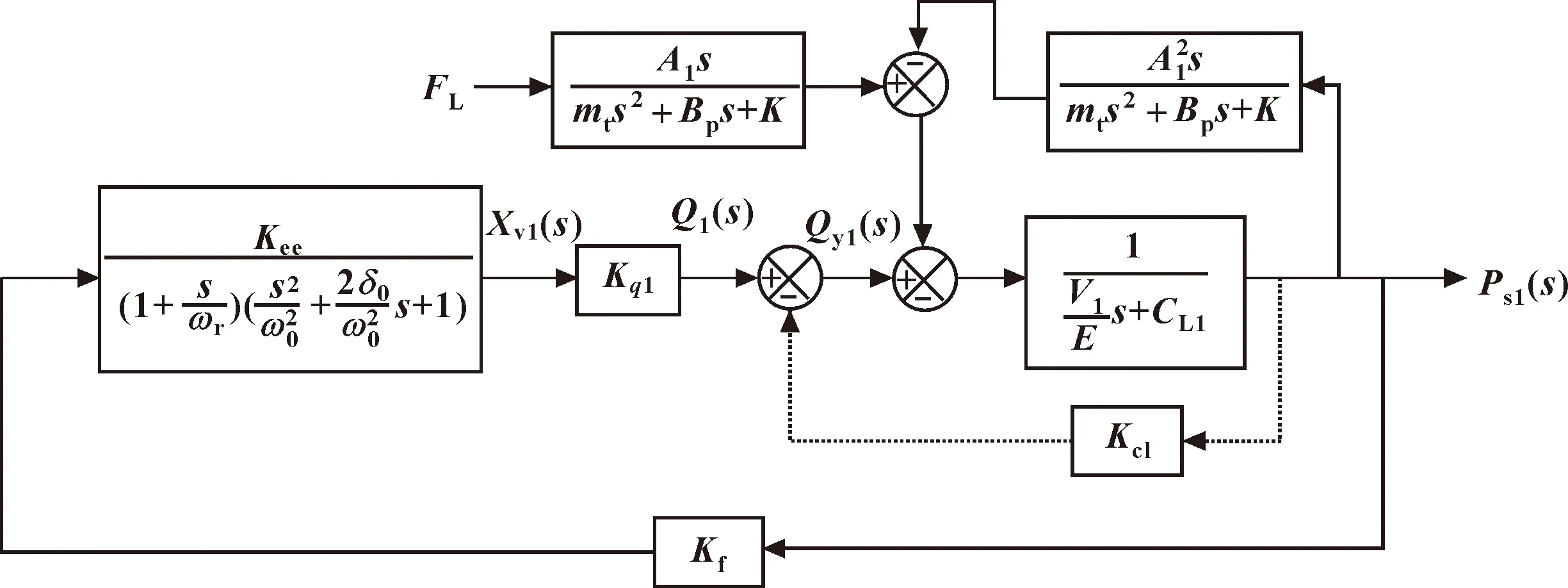
图11 负载力作为输入的系统压力框图
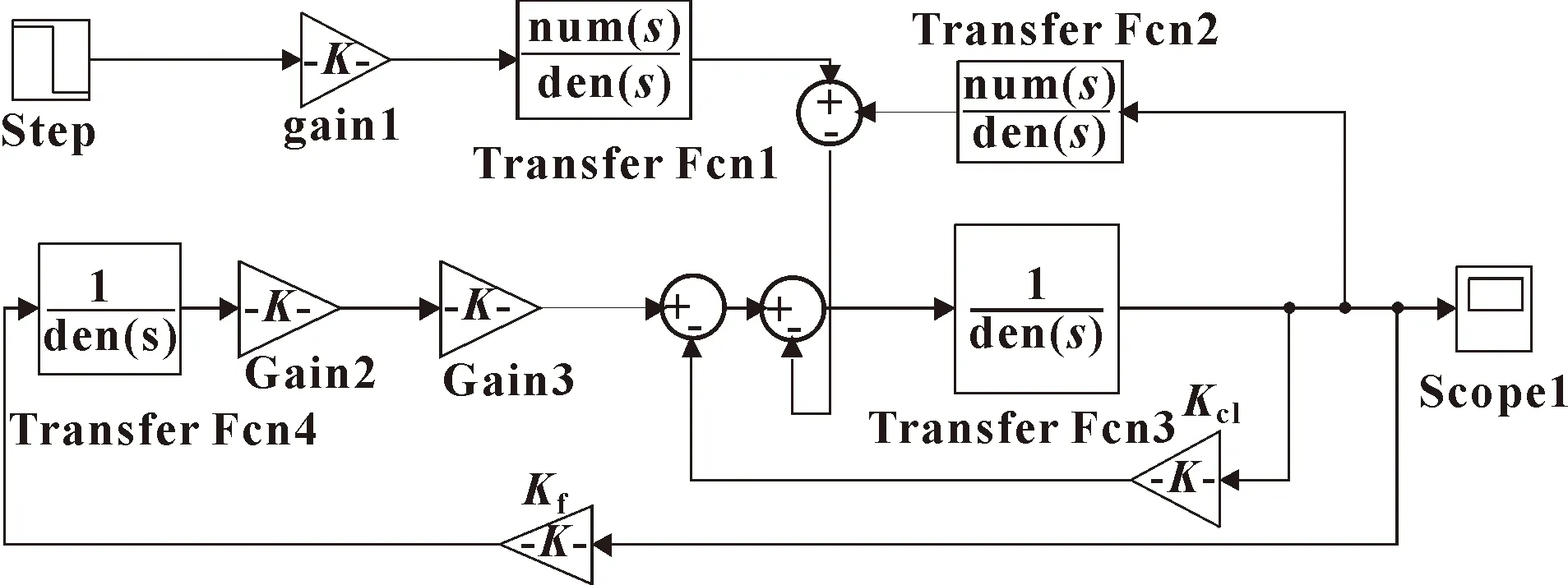
图12 负载力作为输入的系统Simulink仿真模型
图12的仿真模型中将负的阶跃信号作为负载力输入,模拟杆柱在屈曲的瞬间失稳状态,代入仿真参数(同前节)后系统的压力响应如图13所示。

图13 负载力变化对应的系统压力响应
分析图13可知:杆柱在产生屈曲变形之后,确实会产生瞬时的压力损失,与预期中结果相符合。由于此模拟装置液压系统的流量、压力较小,在此模拟装置系统中加入蓄能器,能够有效减小系统的压力波动。
2.4 液压加载系统输出特性建模仿真
结合上述几个仿真模型,最终建立模拟装置的液压加载系统输出特性仿真模型,仿真模型如图14所示。仿真模型以设定信号作为输入,为使模拟结果更贴近实际情况,采样周期设置为0.1 s,增加PID调节器,通过调整和优化参数,减小系统响应的超调量和响应时间。

图14 液压加载系统输出特性的Simulink仿真模型
设定模拟装置压力-时间曲线主要参数如下:周期T=12 s,TU=TD=6 s,TU1=TD1=2 s,最大压力Fmin=600 N,最大拉力Fmax=1 800 N。
为使结果更加清晰直接,代入仿真参数(同前节)后,选取一个周期的仿真结果与预设压力-时间曲线进行对比,如图15所示。
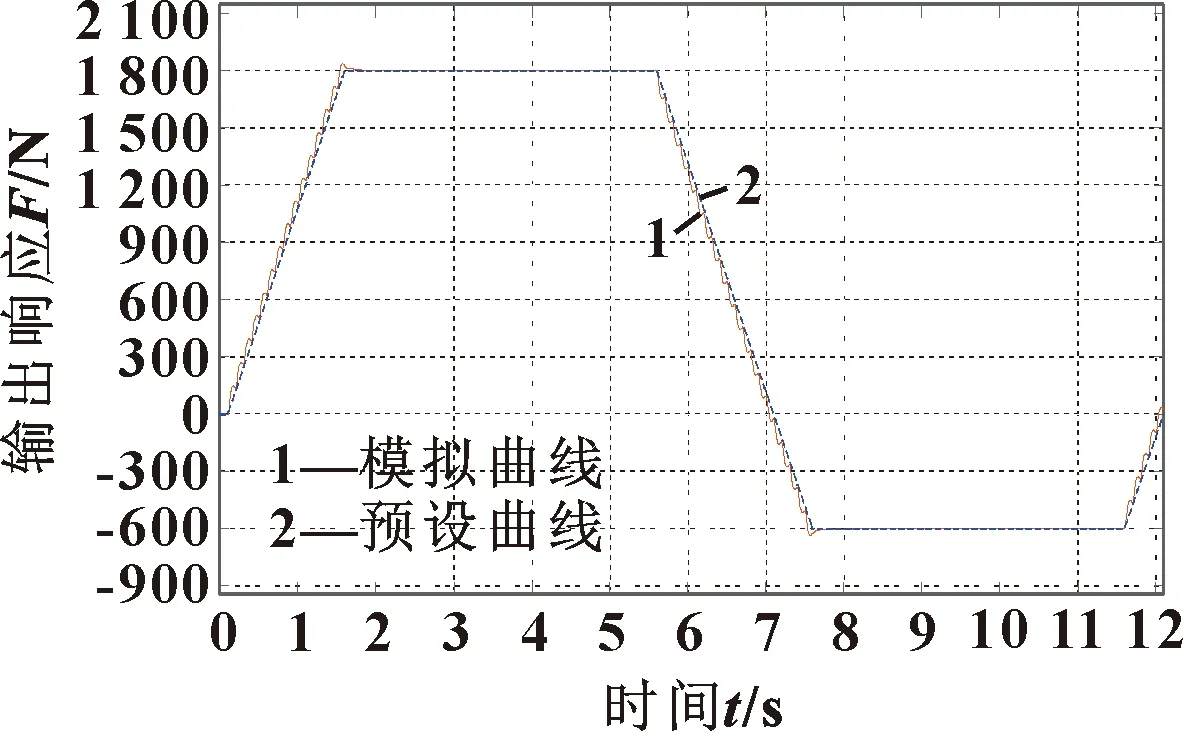
图15 模拟装置输出特性曲线与预设曲线的对比图
从图15可知:仿真曲线和预设曲线在轴向力加载过程中会产生一定的差值,对比数据后发现最大差值出现在加载压力到达最大值转为稳定值时刻,差值约为33.9 N。通过计算得出误差为5.6%,可以满足预期的目标,这也证明模拟装置的设计方案具有可行性。
3 结论
从比例溢流阀入手,对文中模拟装置系统简化后进行液压系统建模,采用Simulink搭建系统仿真模型,得到多组数据仿真结果。通过仿真结果的分析和处理,得到的结论为:
(1)此模拟装置中比例溢流阀具有无级调压能力,系统的开环传递函数伯德图也证明模拟装置具有稳定性;以负载力为输入的建模仿真,证明了负载失稳会造成系统瞬时的压力损失;通过对比模拟装置的输出压力曲线和预设曲线,验证了模拟装置的可行性和可靠性。
(2)由于时间和能力有限,仿真是在相对理想条件下进行的,实际的液压系统工作过程中极易受到温度和油液黏度的影响,模拟结果仍需要后续的试验进行验证。
