阀芯旋转式高速开关阀稳态液动力矩研究

2023-07-27阎宇王鹤陈震丰健刘晋沛张晓宇

机床与液压 2023年13期

阎宇，王鹤，陈震，丰健，刘晋沛，张晓宇

(太原理工大学新型传感器与智能控制教育部重点实验室，山西太原 030024)

0 前言

随着微电子技术的发展，电液数字控制技术成为实现机电一体化的重要手段[1]。高速开关阀作为一种数字阀，通过数字信号控制阀芯的正反向运动完成阀口的启闭，从而实现液流的通断，具有抗污染能力强、价格低廉、应用范围广等优点[2-3]。目前常用的高速开关阀通过驱动阀芯作直线往复运动实现阀口的启闭，存在着阀芯行程与开关频率之间的矛盾。基于此，提出一种阀芯旋转式高速开关阀，通过电机驱动阀芯旋转完成阀口的启闭，从而减少阀芯行程对开关频率的影响。

液动力是影响阀控制精度的重要因素[4]。当流体流经控制阀时，流体的速度及方向发生改变，从而引起流体动量发生变化，最终对阀体产生反作用力，即为液动力[5]，其包括稳态液动力与瞬态液动力，其中瞬态液动力相比稳态液动力较小，一般不予考虑。在高压大流量时，液动力变化显著，易引起阀芯振动，影响阀的控制精度[6]，因此在阀的设计过程中，必须考虑到液动力的影响。

针对稳态液动力，目前已有大量研究。白继平等[7]采用数值计算方法，研究阀芯结构变化对2D高频转阀的阀芯沟槽流体近壁平均压力、平均流速及液动力矩的影响；冀宏等人[8]采用CFD仿真，对2种典型节流槽形式的滑阀进行流场仿真分析，发现在特定阀口开度内液动力会使阀口开度变大；常学森等[9]对新型旋转阀芯液压阀在低压工作条件下的转动力矩进行仿真与试验分析，发现该阀在低压工作条件下结构稳定、转动力矩小；谢海波等[10]研究了不同阀口形态下内流式锥阀所受液动力特性，结果表明阀口形态变化，阀芯所受的液动力方向和大小也发生变化；吕孟[11]应用Fluent对一多路阀斗杆二联进行流场仿真，得到不同工况下的阀芯稳态液动力，揭示液动力随流量及阀芯位移的变化规律；杨庆俊等[12]对一入口节流式滑阀在不同结构参数及不同工作条件下的液动力进行研究，分析液动力变化的内在机制；金伟和史俊强[13]利用Fluent对不同阀芯旋转角度下的流场进行分析，通过阀口流体速度云图、压力云图及流线图分析流体运动规律；王伟[14]运用Fluent仿真软件对一阀芯旋转式四通换向阀内部流场进行动静态仿真分析，探讨阀口压差、阀口形状及阀口开度等对转阀内部流量及液动力的影响。目前针对滑阀与锥阀的液动力研究已有一定成果，但是对转阀的液动力研究还较少，缺少可直接借鉴的成果。

本文作者提出一种阀芯旋转式高速开关阀，采用理论与仿真结合的方法，研究阀芯结构变化对阀口过流面积、流量系数、射流角及稳态液动力矩的影响，得到液动力矩的影响因素及变化规律，并提出液动力矩补偿方法，为有关高速开关阀阀芯结构的优化提供依据。

1 阀芯旋转式高速开关阀结构及工作原理

1.1 结构设计

图1所示为阀芯旋转式高速开关阀三维模型，主要由阀体、阀芯、阀套、端盖、堵头、套筒等零件构成，伺服电机连接阀芯左端的套筒驱动阀芯做旋转运动，步进电机连接阀芯右端的堵头驱动阀芯做轴向运动。阀芯沿轴向布置3个台肩，两端台肩可将阀腔与轴承分隔开，减小轴承受到的液压冲击，同时台肩设有平衡槽，减小阀芯受到的液压卡紧力；中间台肩两侧开有沿圆周方向均匀分布且相互对称的沟槽，数量为8。阀套上沿圆周方向开有与阀芯沟槽相对应的2个窗口，两窗口对应圆心角为180°；阀套上沿轴向共有两列窗口且在圆周方向的位置相同。

1.2 工作原理

阀芯旋转式高速开关阀通过电机驱动阀芯旋转，改变阀芯沟槽与阀套窗口之间的相对位置，实现油路的通断。当阀芯沟槽与阀套窗口有重合时，如图2(a)所示，阀口打开，油液流出；当沟槽与阀套窗口没有重合时，如图2(b)所示，阀口关闭，无油液流出。阀芯旋转不断改变重合部分，实现油液通断，完成高速开关。文中以阀芯轴向位置固定，阀芯沟槽与阀套窗口从刚开始接触到恰好完全分离进行研究，此时阀芯旋转角度为0°～30°。

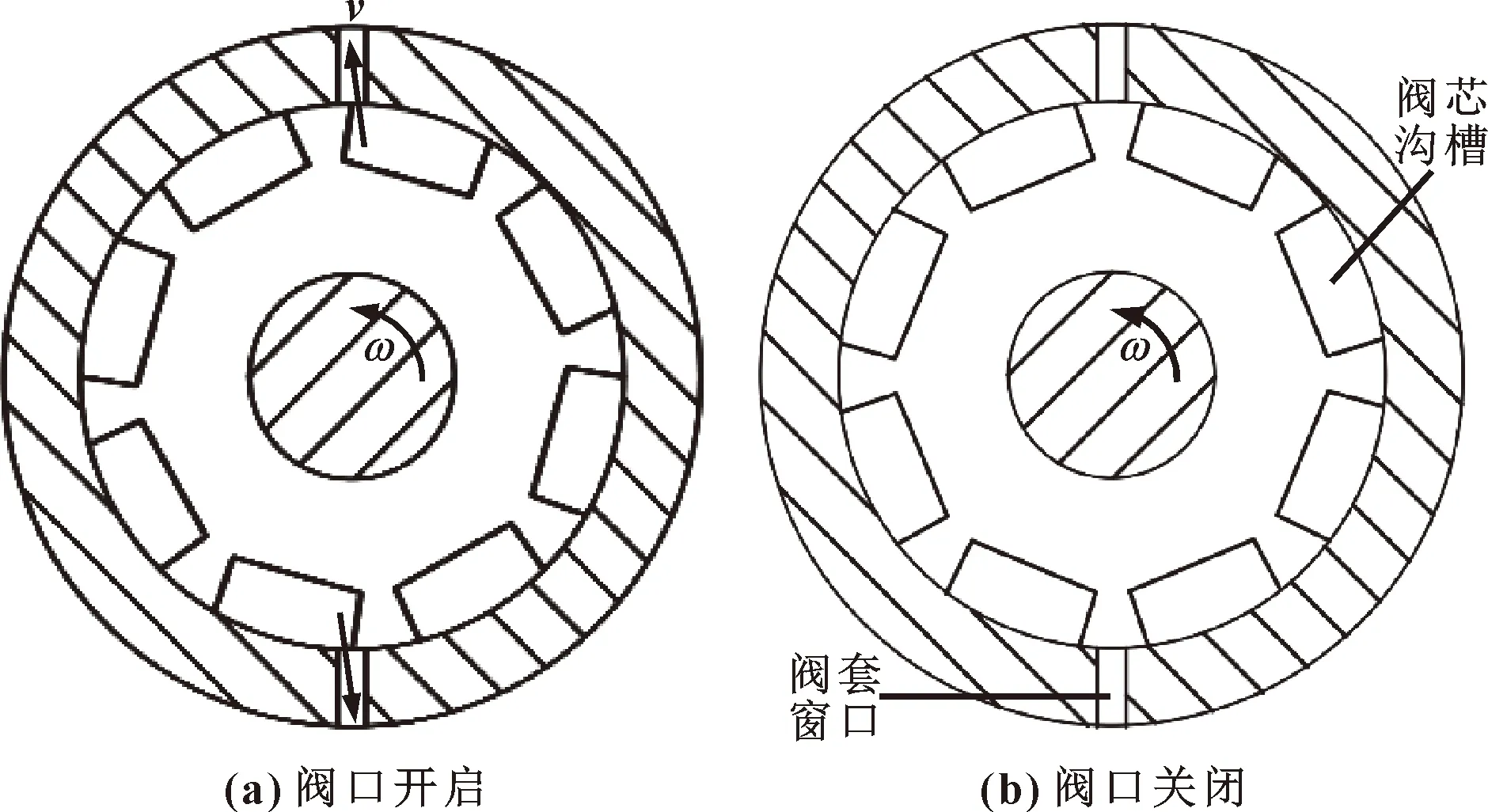
图2 工作原理

2 液动力矩理论计算模型

由于阀芯左右对称，故只研究油液从左端进油口P到出油口T时的情况。阀芯旋转式高速开关阀为上下对称，其所受的径向力互相抵消，阀芯所受的轴向力通过轴承对阀芯的作用力来平衡。油液从P口进入时，其流向总是与阀芯径向重合，而在流出T口时，除了当阀套窗口恰好位于阀芯沟槽正中央时，其余情况油液流向总与阀芯径向及周向形成角度，意味着当油液流入阀腔时，其动量在周向分量为零，流出阀腔时，其动量在周向分量不为零，从而动量发生变化，对阀芯产生液动力。周向液动力表现为扭矩特征，会干扰阀芯旋转，影响阀的工作稳定性。

依据动量定理，得到液动力矩计算公式为

T=-ρqvrcosβ

(1)

式中：ρ为油液密度；q为通过阀口的流量；v为通过阀口速度；r为阀芯半径；β为射流角。

阀口处的平均流速为

(2)

将式(2)代入式(1)，得：

(3)

阀口处的流量为

(4)

式中：Cd为流量系数；Δp为阀口的压差；A为阀口过流面积。

将式(4)代入式(1)，得：

(5)

由式(3)可知，流量一定时，稳态液动力矩与阀口过流面积成反比，与射流角余弦值成正比。由式(5)，压差一定时，稳态液动力矩与阀口过流面积、阀口压差及射流角余弦值都成正比。

阀芯沟槽与阀套窗口有3种位置，如图3所示，阀芯旋转角度从0°增大到15°，阀口过流面积逐步增大，达到最大状态后保持一定时间；阀芯旋转角度为15°时，阀套窗口恰好位于阀芯沟槽正中央；阀芯旋转角度从15°增大到30°，阀口过流面积在保持一定时间的最大状态后，逐步减小到0。

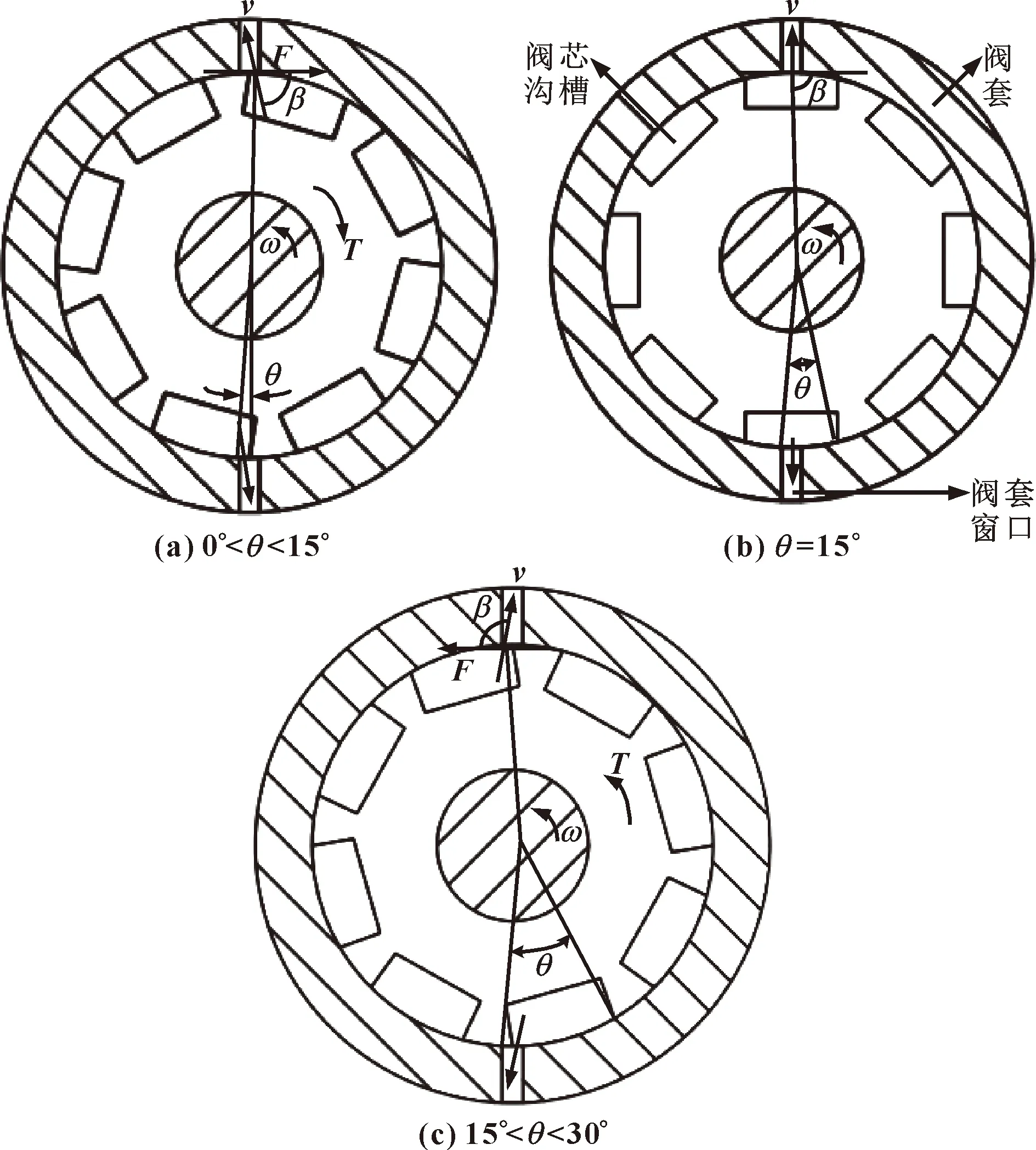
图3 稳态液动力矩示意

定义逆时针为正方向，阀芯逆时针旋转。当阀芯旋转角度0°<θ<15°时，如图3(a)所示，阀芯沟槽位于阀套窗口顺时针方向，根据油液流向，此时阀口处射流角 0°<β<90°，依据式(1)，此时液动力矩为负值，方向顺时针，为阀口关闭方向，是阀芯运动阻力。当θ=15°，如图3(b)所示，此时射流角β=90°，液动力矩为零。当15°<θ<30°，如图3(c)所示，阀芯沟槽位于阀套窗口逆时针方向，此时射流角90°<β<180°，液动力矩为正值，方向逆时针，为阀口关闭方向，是阀芯运动动力。

3 仿真计算

3.1 流场模型

利用SolidWorks建立油液从进油口P到出油口T时的模型，因流场为对称结构，故选取流场模型一半进行研究。图4(a)和图4(b)分别为阀芯沟槽与阀套窗口典型位置时的流场模型。为探究阀套窗口及沟槽形状对液动力矩影响，建立了沟槽三角形、阀套窗口为菱形，沟槽三角形、阀套窗口为三角形，沟槽矩形、阀套窗口为圆形的3种流场模型。为探究阀套窗口边长对液动力矩影响，在沟槽三角形、阀套窗口为菱形的基础上，建立了阀套窗口边长分别为2、3、4 mm的模型。为探究环形槽对液动力矩影响，建立了加工环形槽与不加工环形槽的流场模型，如图4(c)和图4(d)所示。为探究沟槽高度对液动力矩影响，建立了沟槽高度分别为4 mm及6 mm的模型。由于篇幅限制，不再一一赘述。

图4 流场模型

对不同阀套窗口的流场模型，建立了在不同阀芯旋转角度下阀口过流面积的数学模型。

(1)沟槽三角形、阀套窗口菱形

(6)

(2)沟槽三角形、阀套窗口三角形

(7)

(3)沟槽矩形、阀套窗口圆形

(8)

依据建立的阀口过流面积数学模型，计算出在不同阀芯旋转角度下的阀口过流面积，如图5所示。在阀口未完全开启前，随着阀芯旋转角度增大，其阀口过流面积呈增长趋势。由图5(a)可知，阀芯旋转角度一定时，阀套窗口边长越大，其过流面积越大；由图5(b)可知，阀芯旋转角度一定时，不同形状的阀套窗口过流面积由大到小依次为圆形、菱形、三角形，且都在阀芯旋转角度为6°时，其过流面积达到最大，此时阀口刚好处于完全打开状态。

图5 阀口过流面积

3.2 网格划分

划分网格时，采用ANSYS中的Mesh模块，将网格设置为四面体网格，与阀套窗口相连的沟槽壁面因需进行压力积分以计算液动力矩，故对其细化，划分网格如图6所示。

图6 网格划分

3.3 仿真参数设置

将网格导入Fluent，采用压力基稳态求解器。湍流模型选取Realizableκ-ε，壁面函数选取标准壁面函数。流动介质选用液压油，密度880 kg/m3，动力黏度0.036 kg/(m·s)。

探究阀口压差对液动力矩影响时，将入口压力分别设置为1、5、10、15、20、25 MPa；探究阀口流量对液动力矩影响时，将入口流量分别设置为10、20、30、40、50、60 L/min。探究压差一定，阀芯结构变动对液动力矩影响时，将入口压力设置为10 MPa；探究流量一定，阀芯结构变动对液动力矩影响时，将入口流量设置为20 L/min。

3.4 仿真计算模型

采用压力积分的方法，对液动力矩进行求解。如图7所示，将沟槽壁面分别命名为wall-1和wall-2，其液动力矩仿真计算模型为

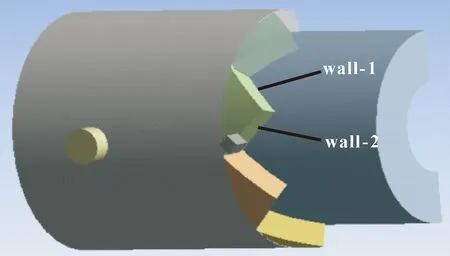
图7 仿真计算模型

T=-(p1-p2)SRsina

(9)

式中：p1为wall-1的平均压力；p2为wall-2的平均压力；S为wall面积；R为沟槽壁面半径；a为壁面与轴线的夹角，沟槽为三角形时a为45°，沟槽为矩形时a为90°。

4 仿真结果分析

基于上述液动力矩理论计算模型，主要研究阀芯结构参数变动对射流角、流量系数及液动力矩的影响，并得到液动力矩的影响因素，提出液动力矩补偿方法。

4.1 射流角

通过CFD-Post获取其周向射流角，图8所示为阀口压差10 MPa、沟槽为矩形、阀套窗口为圆形的流场模型在不同阀芯旋转角度下的射流角。可以看到：当阀口未完全打开即θ≤6°时，随着阀芯旋转角度增大，射流角逐渐靠近90°；当阀口逐渐关闭即24°≤θ≤30°时，随着阀芯旋转角度增加，其射流角越来越偏离90°；而当阀口处于完全打开状态即6°<θ<24°时，随着阀芯旋转角度变化，其射流角变化不大。

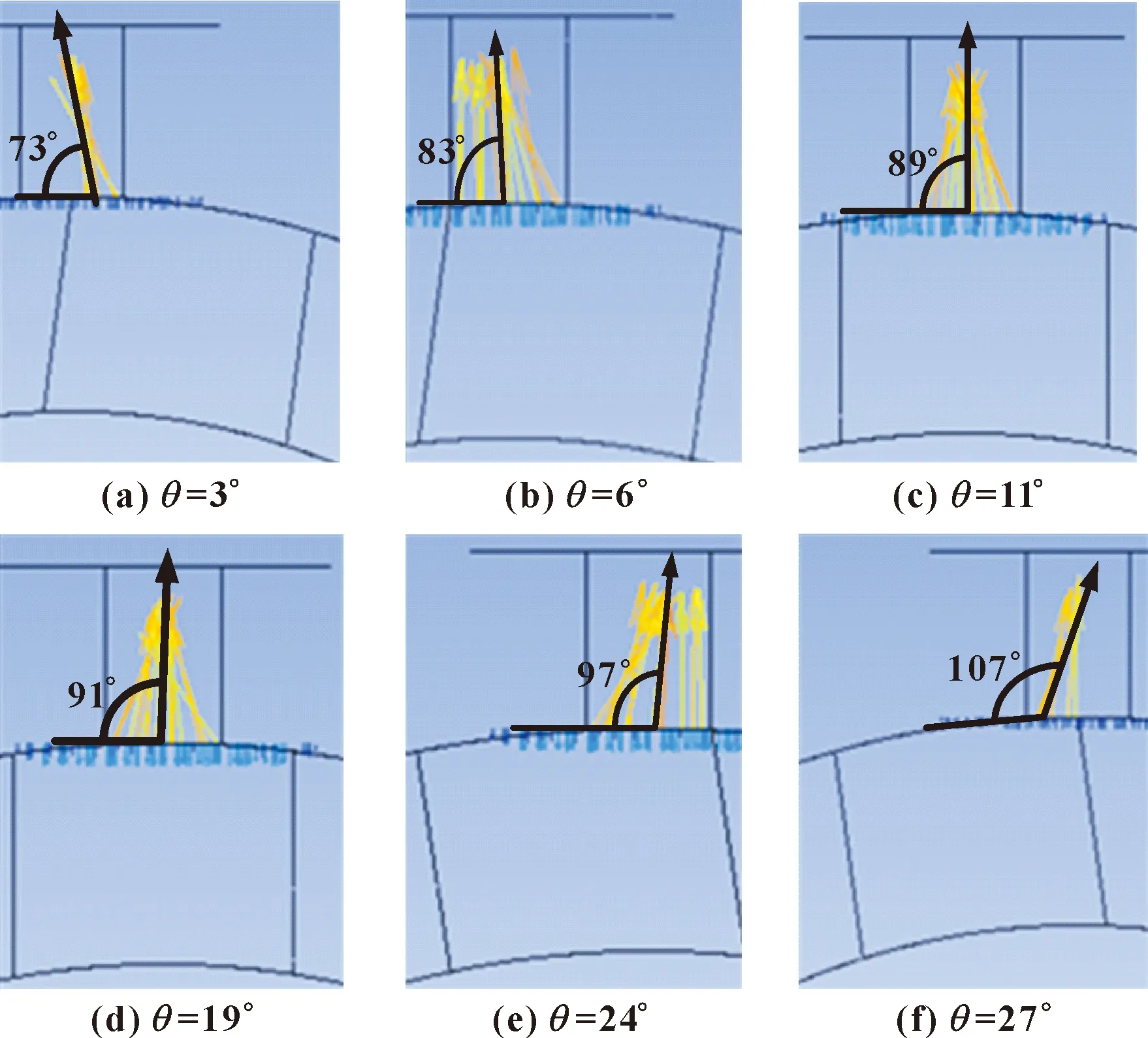
图8 不同阀芯旋转角度下的速度矢量

同理可获得其余条件下的射流角，因阀口打开与关闭状态其射流角呈对称关系，故只探讨阀口打开状态。由图9可以看到：阀芯旋转角度一定，阀口边长越大，射流角越偏离90°；阀套窗口为圆形的，其射流角偏离90°程度最大，而三角形最小；加工环形槽的阀，在阀芯旋转角度小于6°时，其射流角偏离90°的程度与不加工环形槽的阀相比先小后大，阀芯旋转角度大于6°时情况相反；沟槽越高，在阀芯旋转角度小于6°时其射流角越靠近90°，阀芯旋转角度大于6°时相差不大。

图9 不同条件下射流角

4.2 流量系数

流量系数反映阀口局部的液阻特性，流量系数越大，液阻越小，相同压差下通过阀口流量越多[15]。流量系数不能通过阀的结构直接获取，但可以通过CFD仿真获得阀口处的压降及流量，从而间接获得流量系数。根据式(4)得到流量系数的计算公式：

(10)

文中通过将压差设定为10 MPa，流量q通过Fluent报告获取，从而获得流量系数。图10所示为不同阀芯结构的流量系数，可以看到阀口未完全打开，随着阀芯旋转角度增大，其流量系数整体呈下降趋势。阀口处于完全打开状态时，其流量系数在某一数值上下波动。当阀芯旋转角度关于θ=15°对称，其流量系数也对称。针对不同结构的阀芯，也可以发现：阀套窗口边长越大，整体上其对应的流量系数越小。阀套窗口形状不同，其流量系数差异较大，阀口未完全打开前，流量系数由小到大依次为圆形、菱形、三角形；阀口完全打开后，阀套窗口为三角形的流量系数先减小后基本不变，而菱形和矩形的基本不变。加工环形槽的流量系数与不加工环形槽相比，其变化趋势一致，只是加工环形沟槽流量系数较大。沟槽高度不同，其流量系数变化趋势一致且相差不大。

图10 不同条件下流量系数

4.3 液动力矩

通过液动力矩理论计算及CFD仿真得到液动力矩计算数值，探究阀口压差、流量及阀芯结构参数变动对液动力矩影响。

图11是阀芯旋转角度为3°时不同阀套窗口压差下的液动力矩，可以看到液动力矩与阀口压差成正比。由于压差一定时液动力矩与阀口过流面积及射流角余弦值成正比，在阀芯旋转角度为3°时，不同阀套窗口的射流角余弦值由大到小依次为圆形、菱形、三角形，阀口通流面积由大到小依次为圆形、菱形、三角形，故阀套窗口为圆形的液动力矩最大，阀套窗口为三角形的液动力矩最小。图12是阀芯旋转角度为3°时不同阀套窗口流量下的液动力矩，可以看到液动力矩与流量的二次方成正比。由于流量一定时液动力矩与射流角余弦值成正比，与阀口过流面积成反比，液动力矩最终呈现阀套窗口为圆形的最大，三角形的最小，说明流量一定，阀套窗口形状不同，对液动力矩影响最大的因素是射流角。

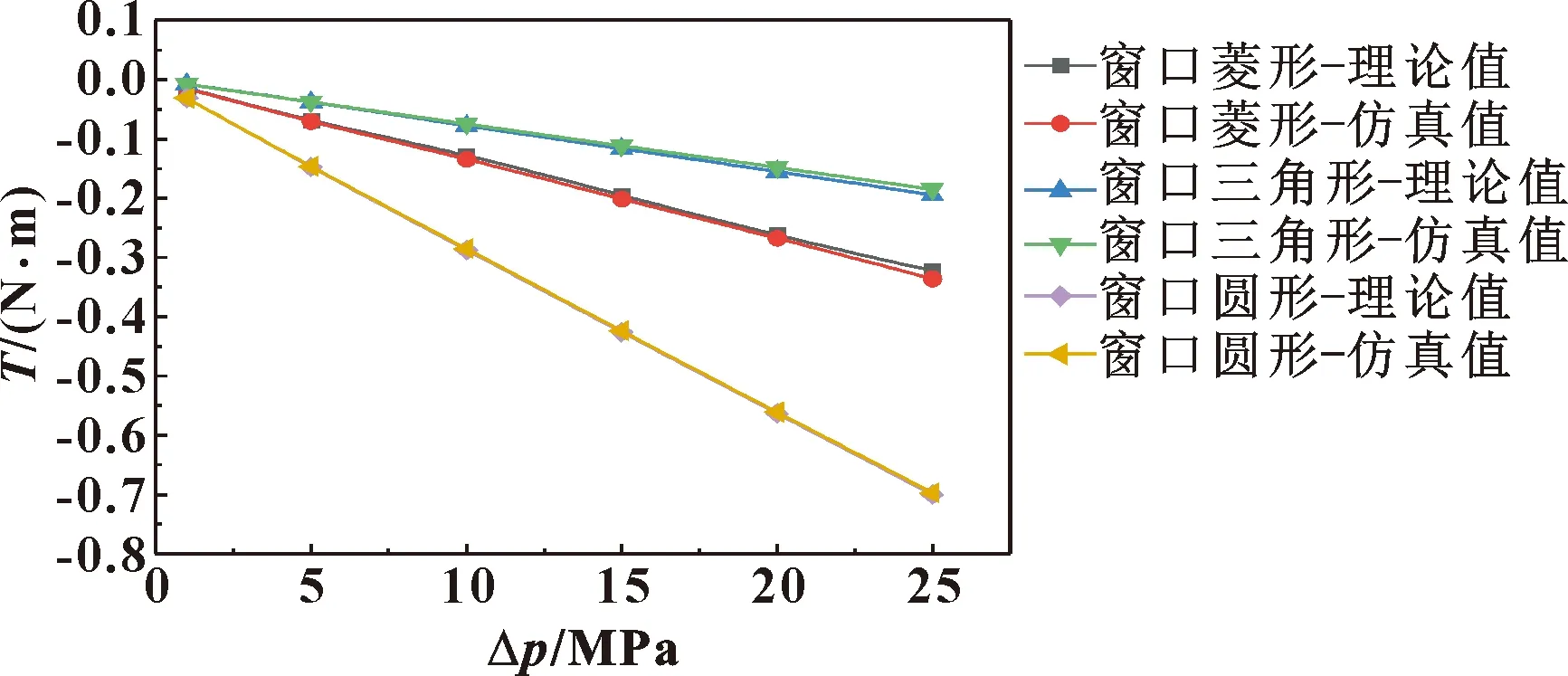
图11 不同阀套窗口压差下的液动力矩

图12 不同阀套窗口流量下的液动力矩

图13是阀口压差10 MPa、阀套窗口边长不同的液动力矩。压差一定时，随着阀芯旋转角度增大，液动力矩也增大，是因为阀口过流面积逐步增大的缘故；之后减小，是因为随着阀芯旋转角度增大，射流角逐渐靠近90°。阀套窗口边长越大，液动力矩越大，也是因为压差一定时液动力矩与阀口过流面积成正比。图14是阀口流量为20 L/min、阀套窗口边长不同的液动力矩。流量一定时，随着阀芯旋转角度增大，液动力矩逐渐减小，且都在阀芯旋转角度较小时减小速度较大，主要是因为此时阀口过流面积逐渐增加，射流角逐渐靠近90°。当阀口完全开启后，液动力矩逐渐趋于零，主要是因为此时射流角接近90°。阀芯旋转角度一定时，阀套窗口边长越小，其液动力矩越大，主要是因为流量一定时，液动力矩与阀口过流面积成反比。

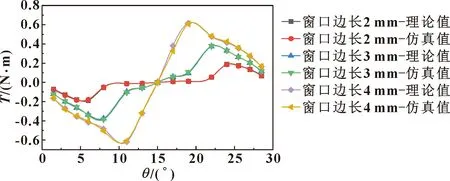
图13 压差一定，不同阀套窗口边长的液动力矩

图14 流量一定，不同阀套窗口边长的液动力矩

图15是阀口压差10 MPa、阀套窗口形状不同的液动力矩。压差一定时，随着阀芯旋转角度增大，阀套窗口为菱形及圆形的液动力矩先增大后减小，而阀套窗口为三角形的液动力矩变化不大。分析图5和图9可知：改变阀套窗口形状，射流角余弦值由大到小依次为圆形、菱形、三角形，阀口过流面积由大到小依次为圆形、菱形、三角形，而在压差一定时，液动力矩与阀口过流面积及射流角余弦值成正比，故压差一定时，液动力矩由大到小依次为圆形、菱形、三角形。图16是阀口流量为20 L/min，阀套窗口形状不同的液动力矩，液动力矩在满足逐渐减小为零的同时，发现阀套窗口为菱形及三角形的液动力矩较小，而圆形的液动力矩最大，根据图12的分析，此时液动力矩的影响因素主要是射流角。

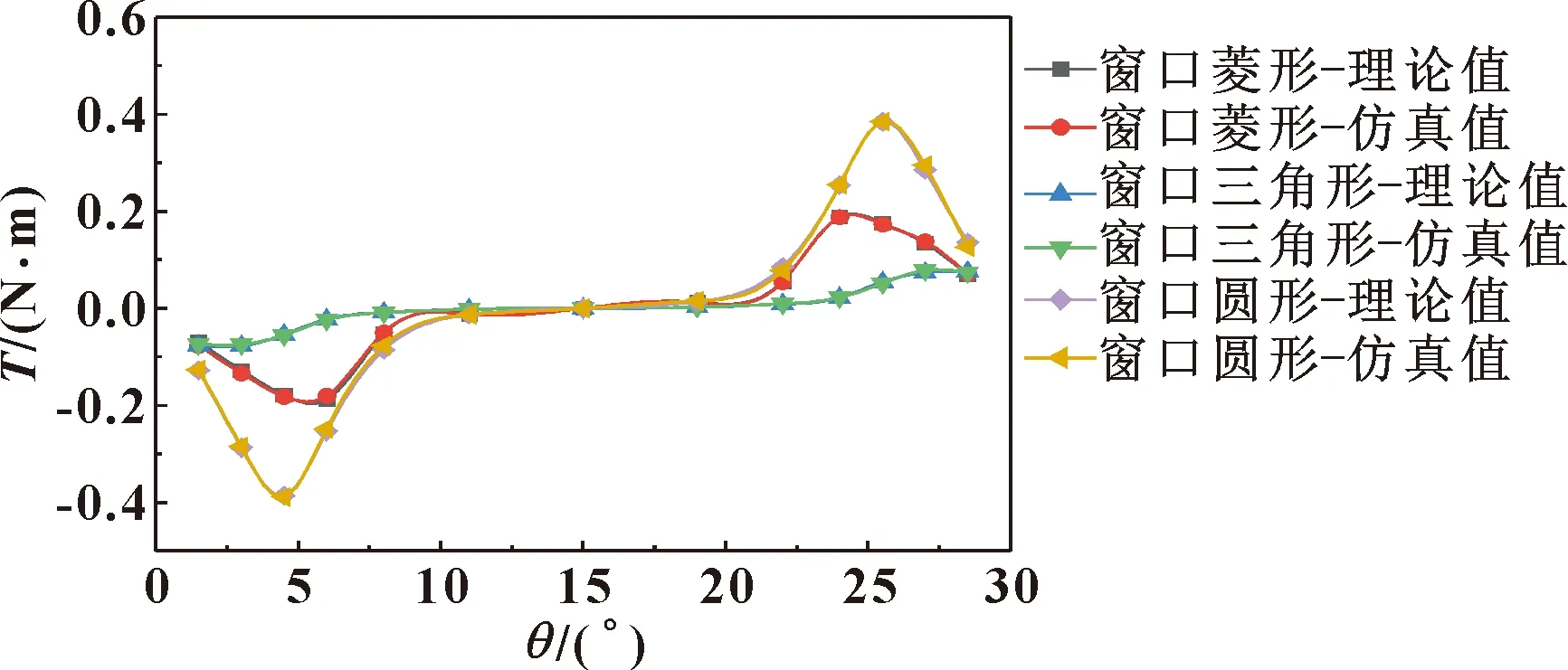
图15 压差一定，不同阀套窗口的液动力矩

图16 流量一定，不同阀套窗口的液动力矩

图17是阀口压差10 MPa、加工环形槽与不加工环形槽的液动力矩。压差一定时，加工环形槽的液动力矩在阀口刚好完全打开时处于最大，而不加工环形沟槽的阀在阀口未完全打开时其液动力矩便处于最大。此外，在阀口未完全打开时，加工环形槽的阀较不加工环形槽的阀，其液动力矩先小后大，主要是由于加工环形槽的阀，其射流角余弦值较不加工环形槽的阀先小后大。图18是阀口流量为20 L/min，加工环形槽与不加工环形槽的液动力矩。流量一定时，液动力矩在满足逐渐减小规律的同时，加工环形槽的液动力矩较不加工环形槽的小，同理也受到射流角影响。