一种轻型仿人机械臂关节并联机构设计

王文萍，刘伟潮

(广州城市理工学院机械工程学院，广东广州 510000)

0 前言

机器人行业逐渐成为“中国制造2025”和“工业4.0”时代下代表一个国家科技创新和高端制造行业水平的行业。目前协作型机器人的类型主要有主动柔顺控制型、被动柔顺型和轻量化绳驱动型[1]。前两种柔顺型机器人通过人机交互过程进行柔顺响应，仿人协作轻量绳驱动机械臂将成为未来协作型机器人的研究重点。文献[2]提出一种新型的通过绳索驱动、压缩弹簧支承的柔性并联腕部康复机构，保证人体腕部生理运动空间处于机构有效工作空间之中。文献[3]为获得更好的柔性度，设计使用气体动力肌肉模拟腕关节的康复机器人；文献[4]设计一气动腕关节外骨骼康复机器人，构建三自由度并联机构；文献[5]提出一种将动、静平台通过一个球副与绳索牵引实现腕关节的运动功能；文献[6]提出一种3-RRR球面并联机构，以机构的雅可比矩阵条件数为优化对象，进行遗传算法设计；文献[7]设计了一款绳索混合驱动并联机构，并对并联机构运动学进行分析，得出动平台位姿与绳索长度的关系满足运动学反解模型；文献[8]提出一种绳驱动并联机械臂位姿正解的Dogleg算法迭代方法；文献[9]设计一种3-PRC并联机构，并对该并联机构进行MATLAB、ADAMS、Por/E多软件联合建模与运动学仿真；文献[10]引用一种三维切片法用于分析并联机构末端在实际工作空间中高度与偏转角的运动性能。

根据人体上肢手臂腕关节的解剖学结构及运动特点，设计带有多个支链连杆结构的腕关节并联机构。利用MATLAB进行结构参数筛选优化，得出该并联机构运动学模型，验证该腕关节并联机构的可行性与设计方法的合理性。

1 并联机构结构设计

1.1 人体腕关节的结构特点

人体腕关节运动形式主要有前屈后伸与外展内收以及小范围旋转运动[11]。如图1所示，从解剖学角度确定手腕转动方向是通过将手掌自然伸展；手掌向大拇指的旋转运动为桡屈，向小拇指方向的旋转运动为尺屈，向手肘内侧的旋转运动为屈曲，向手肘外侧的旋转运动为背伸；同时手腕向身体内侧与外侧的旋转运动分别为内旋与外旋。

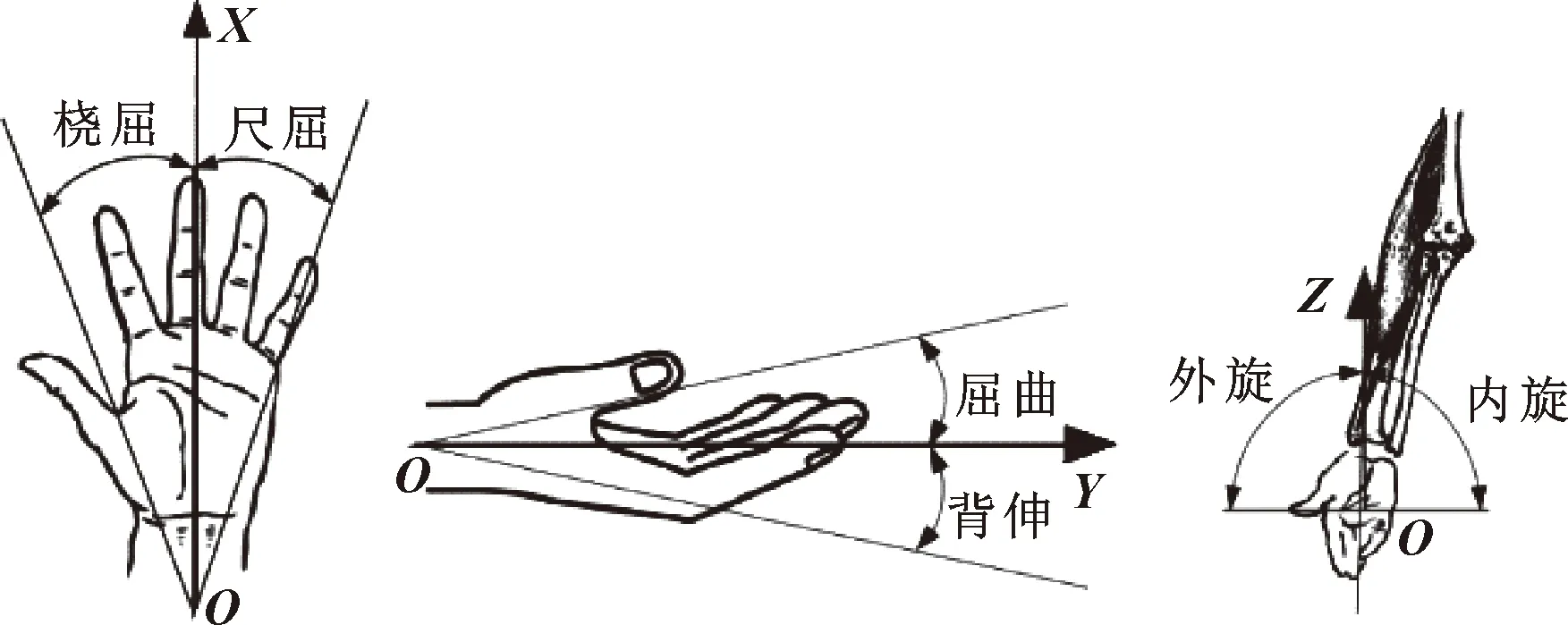
图1 腕关节的解剖学结构及运动特点

为使腕关节工作空间与人体手腕的工作空间相似，优化腕关节并联机构工作可行性，设置与腕关节旋转角度相似的设计要求，如表1所示。

表1 腕关节并联机构的基本运动范围

1.2 腕关节并联机构主体设计

文中研究的并联机构主要应用于轻量绳驱动协作机器人腕关节模块的三自由度并联机构，如图2所示。腕关节并联机构三维模型、简化模型与机构简图分别如图3、图4与图5所示。其中腕关节并联机构的机械原理结构为三自由度的3-RRRR-(UPU)并联机构，其中R表示转动副，P表示移动副，U表示虎克铰。腕关节并联机构主体由动静平台、连接动静平台的4根弓形连杆、UPU连杆串联机构、滑轮安装架、驱动滑轮组与腕关节末端手爪安装法兰组成。同时为避免长时间使用后，绳索张力失效对腕关节并联机构运动产生不良影响，本文作者在机械臂中设计了一套自适应绳索张紧装置，如图6所示。

图2 轻型仿人绳驱动机械臂总体装配

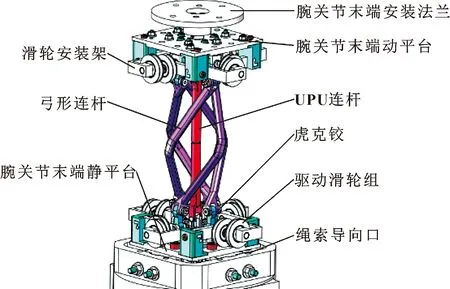
图3 腕关节并联机构整体三维模型

图4 腕关节并联机构简化模型

图5 腕关节并联机构简图

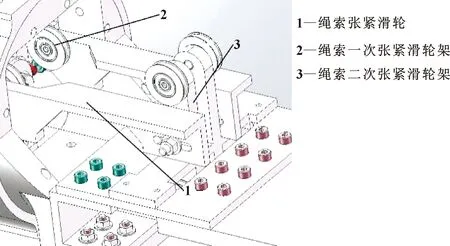
图6 绳索张紧机构模型示意

腕关节并联机构静平台中的旋转滑轮带动UPU连杆实现腕关节并联机构末端手爪法兰绕腕关节末端坐标系的Z方向进行滚动运动，模拟人体手臂外旋/内旋运动特点；绳索连接动静平台，通过滑轮组一端固定于静平台，另一端固定于动平台，通过牵引其中一端改变动静平台距离，改变腕关节末端动平台位姿，实现末端机构绕X轴与Y轴滚动，完成模仿人体腕关节桡屈/尺屈、背伸/屈曲运动，实现末端平台作球面纯滚动，如图7与图8所示。弓形连杆与动静平台通过铰链连接，随动平台、静平台位姿关系变化而转动。通过绳索牵引实现对手爪的灵活控制，腕关节末端手爪法兰的位姿状态与机构运动形式可实现模仿人类手腕动作的仿生运动。

图7 腕关节并联机构末端动平台桡屈/尺屈的运动仿真

图8 腕关节并联机构端动平台背伸/屈曲运动仿真

根据Grubler-Kutzbach公式，计算腕关节并联机构可动度：

(1)

设定当并联机构静平台固定不动时，计算关节并联机构的自由度数目。令n表示并联机构中连杆的数量，g表示并联机构中关节的数量，对于第i个关节，ui表示该关节约束数目；引入fi表示该关节自由度数目，空间结构中ui=6-fi。简化式(1)，通过各个关节自由度之和以及关节数量与并联机构自由度关系可知：

(2)

将n为14、g为16、机构中所有关节自由度数目之和为20，代入式(2)中得腕关节并联机构自由度为2，满足实现并联机构绕X轴与Y轴的运动要求。腕关节并联机构通过贯穿动静平台几何中心的UPU连杆实现并联机构绕Z轴转动，增加1个可动度，整体并联机构可动度为3，符合人体手腕三自由度的运动特征，满足设计要求。

1.3 腕关节并联机构原理分析与误差优化

为简化运动算法，同时便于控制以及提高定位精度，将曲形杆与并联机构动静平台相连的铰链均布于直径为S的圆上。腕关节并联机构的原理是通过相对两根连杆相互交叉，并与并联机构的静平台以及动平台形成一个以动静平台为底边、曲形杆为斜边的直角三角形，构成直角三角形的斜边两两相交，交点随动平台相对静平台作球面纯滚动形成椭圆运动轨迹。图中S为动静平台上铰链均布圆的直径，L为曲形杆铰链中心连线长度且为直角三角形斜边，R为动静平台几何中心点距离，此时两个直角三角形构成一个矩形，图9虚线表示交点运动形成的椭圆形轨迹。

图9 交点的运动轨迹

由于并联机构动平台末端运动轨迹形成椭圆，椭圆轨迹各点曲率变化导致末端随着动平台做球面滚动时出现ZW方向距离变化，驱动绳索的松紧度呈现非线性变化，引发张力失效。为实现驱动绳索平稳控制动平台的运动角度与速度，拟以圆形运动轨迹逼近椭圆运动轨迹达到机械臂设计精度要求，减少误差，同时降低对腕关节并联机构的运动模拟难度，提高可控度。

如图10所示，图中点C为虚拟等效圆圆心，设置在距离坐标原点为D的Z轴负半轴。以点C到交点的距离为r做等效圆，假设由一直线经过点C并与椭圆相交于Pe，与等效圆相交于点Pc。由以上条件可知直线、等效圆与椭圆方程分别为

图10 椭圆与虚拟圆示意

f(x)=tanA·x+D

(3)

x2+(z+D)2=r2

(4)

S2+R2=L2

(5)

(6)

公式(3)为过点C到并联机构极限位置时的交点直线方程；公式(4)为以点C为圆心的虚拟圆方程表达式；公式(5)为S、R以及L的关系式；公式(6)为交点的椭圆轨迹方程。联立以上方程可求直线分别同椭圆及等效圆的交点坐标。如图10所示，可得椭圆与等效圆之间距离d：

d=f(x，z)=[(xc-xe)2+(zc-ze)2]1/2

(7)

d值接近于0时，并联机构可形成绕等效圆的纯滚动运动。考虑实际加工条件，可将d值误差控制在0.03 mm以内或更低以获得更高运动精度，文中拟设定误差为0.03 mm。运用SoildWorks对d值条件进行编程仿真分析，模拟出不同S值下D值的变动对并联机构的误差d影响，SoildWorks与MATLAB联合仿真。具体联合仿真的数据采样流程如图11所示。

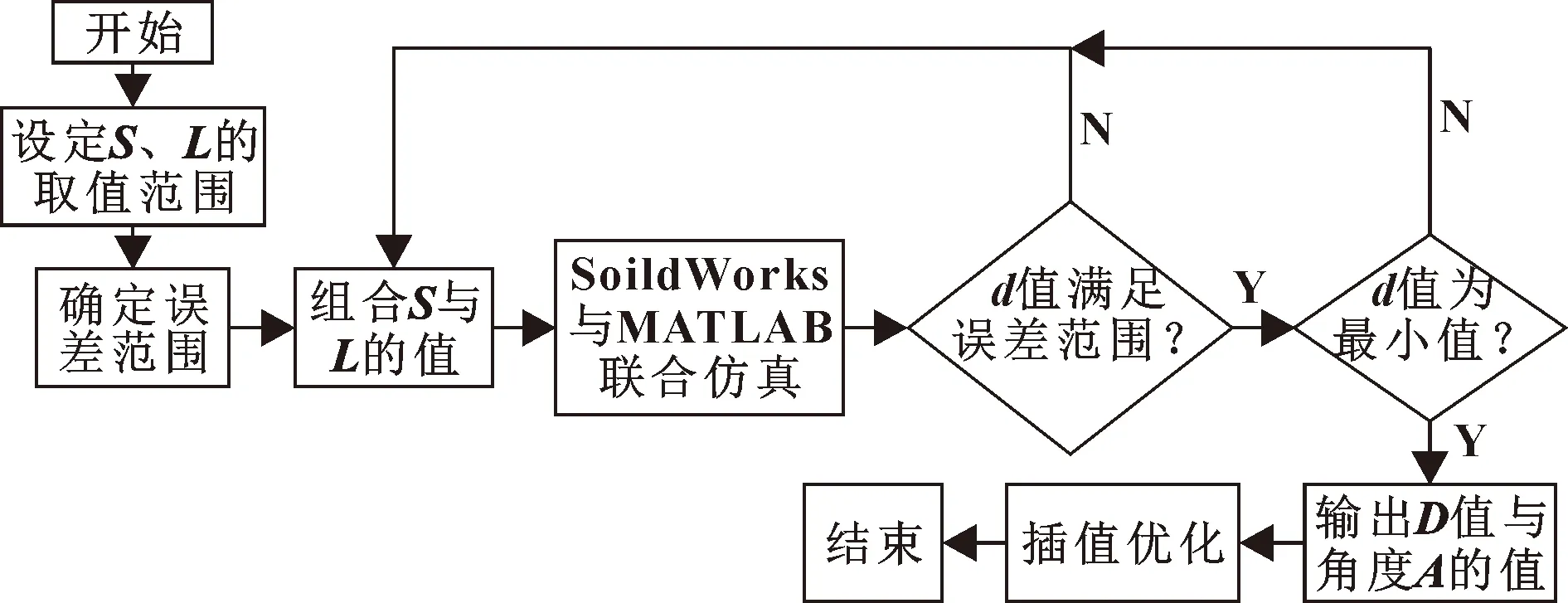
图11 仿真数据采样流程

仿真分析可知：当S取值为[30，55]mm，弓形连杆长度L的取值区间为[110，130]mm，可得满足并联机构设定误差时D的数值分布。用MATLAB对采集数据进行插值优化处理，如图12所示。仿真模拟可得两点相交直线与Y轴之间角度A的分布图，插值优化处理后如图13所示。对仿真获得数据进行插值优化可知：在腕关节并联机构设计中，考虑机械零部件安装及运动精度要求，将并联机构S设定为40 mm，确定D数值为3.1 mm时，动静平台之间最大误差值为0.02 mm，符合并联机构设计及加工要求。

图12 对D值的数据采集(a)及插值优化模型(b)

图13 角度A的数据采集(a)及插值优化模型(b)

2 腕关节并联机构运动学分析

2.1 腕关节模块并联机构正运动学分析

将腕关节模块并联机构分为上下两个部分，并联机构上部分为末端动平台，并联机构下部分为固定平台即静平台，如图14所示。

图14 并联机构运动学简图

以并联机构固定平台的转动几何中心点O为固定坐标系原点，X轴与Y轴设置在并联机构静平台上，Z轴垂直于静平台平面。以动平台几何中心点O′为坐标系原点，X′轴与Y′轴设置在并联机构动平台平面上，使X′轴平行且同向于固定坐标系O-XYZ的X轴。连接点O与点O′，使θ1为垂直于并联机构静平台方向上OO′投影与固定坐标系O-XYZ上X轴之间的夹角。θ2表示俯仰角即OO′相对固定坐标系Z轴的夹角。由此可知，并联机构动平台坐标系O′-X′Y′Z′相对于并联机构静平台固定坐标系O-XYZ的空间位姿可用两个角度与一个平移位移表示，即绕Z轴旋转角度为θ1、绕当前Y轴旋转角度θ2与沿坐标系Z轴平移距离h。旋转-平移矩阵的齐次方程表达式为

其中：RZ(θ1)表示沿坐标系Z轴的旋转矩阵的齐次表达式，具体为

(8)

RY(θ2)表示沿坐标系Y轴的旋转矩阵齐次表达式，具体为

(9)

TZ(h)表示沿坐标系Z轴平移的齐次表达式，具体为

(10)

式中：Ci表示cosθi，Si表示sinθi。

将平移-旋转的齐次矩阵表达式相乘得到：

(11)

2.2 腕关节并联机构绳驱动运动学分析

使用N型绳驱动构型如图15所示，使用单个驱动电机控制关节实现单自由度运动，N型绳驱动构型使用一条绳索作为驱动绳索，不考虑外界因素对绳索长度影响，绳索伸长量与收缩量相等[12]。

图15 N型绳驱动构型

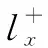
(12)

联立公式(9)与(10)，结合绳索长度与末端动平台空间变换齐次矩阵的转换关系，得到绳索长度变化量与末端动平台位姿关系的角度关系为

(13)

其中K与V分别代表末端动平台绕X轴与Y轴的偏转，将式(13)与式(11)代入矩阵可得

2.3 腕关节并联机构逆运动学分析

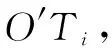
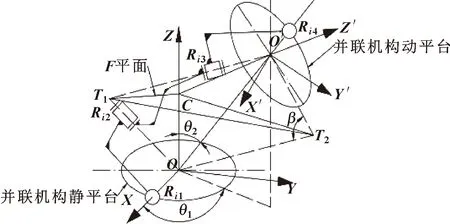
图16 腕关节并联机构支链运动简图

(14)

通过第2.1节正运动分析得到LOO′、LCTi与LCTi+1为

其中：α1与α2为转动副R11以及R21转动角度。联立式(14)得各个转动副Ri转动角度αi：

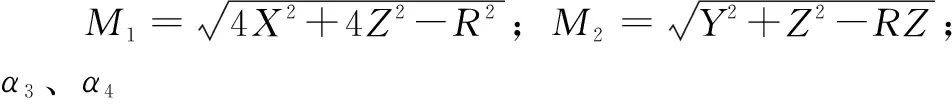
3 结论

根据人体上肢手臂腕关节解剖学结构及运动特点，设计一种有多个支链连杆结构的腕关节并联机构。通过4条连杆支链以及4根绳索，形成并联机构支撑与驱动结构，实现人体手臂腕关节2个可动度的仿生设计，最终通过UPU支链实现腕关节并联机构三自由度运动。其腕关节并联机构的运动可行性与可动度通过G-K公式进行验算，验算结果正确。

分析腕关节并联机构运动轨迹，提出腕关节并联机构动平台的运动函数方程。分析方程，构建并联机构误差数学模型，基于SoildWorks与MATLAB进行联合仿真与数据采集，插值法优化处理采集数据，获得S与L的范围及最优参数组合，结果显示末端动平台在运动角度为±90°时，D=3.1 mm时误差最小。

腕关节并联机构通过Denavit-Hartanberg分析，推导出末端动平台坐标系与并联机构静平台固定坐标系的变化关系数学表达式，完成并联机构的正、逆运动学分析；基于运动分析结果，引入绳驱动关于末端动平台位姿变化的绳索变化关系研究，推导出绳索伸缩量与末端位姿角度变化的函数表达式，进一步验证腕关节并联机构可行性与运动学分析的合理性。