基于LESO的永磁伺服系统无模型无差拍电流预测控制

姜晨艳，李德义，朱其新，3，张国平

(1.苏州科技大学机械工程学院，江苏苏州 215009；2.济南工程职业技术学院科技处，山东济南 250220；3.建筑智慧节能江苏省重点实验室，江苏苏州 215009；4.深圳市大族机器人有限公司，广东深圳 518058)

0 前言

永磁同步电机(Permanent Magnet Synchronous Motor，PMSM)是一个多变量、强耦合、非线性的执行机构，广泛应用于机器人、航空航天、数控机床等伺服控制领域[1-2]。为进一步提高PMSM在伺服控制系统中的性能，研究人员提出了自适应控制、预测控制、神经网络控制等多种高性能控制策略[3]。在众多控制策略中，PI控制是最早被实用化的控制方法，尽管如今现代智能控制算法在伺服控制领域取得了重大发展，PI控制在工业应用中仍是伺服控制的首选[4-5]。

PI控制器的参数整定对系统建模的精确度要求较高，模型越接近实际伺服系统，控制效果越好。但受工况和运行温度影响，电机在运行过程中，内部参数会发生漂移，此时系统的理论数学模型与实际不匹配，进而会导致控制精度降低[6]，严重时甚至会使系统运行失稳。与PI控制方法比较，预测控制更能适应实际过程，所需的模型只强调预测功能而不必苛求结构形式，建模相对简单方便，且可同时满足系统的多个约束条件和非线性特性，适用于多变量系统，受到了业界学者的广泛关注[7]。预测控制结合系统建立的模型对系统未来时刻的状态变量进行预测，对比参考信号与预测值，根据最优准则选取使价值函数最小的最优操作[8]。

为建立不依赖于PMSM参数的预测控制模型，降低参数漂移对控制模型的影响[9-11]，引入无模型控制 (Model Free Control，MFC)[12]。MFC只涉及系统的输入和输出，同时考虑系统的已知扰动与未知扰动，有效降低了模型对系统参数的依赖，从而提高了系统的控制性能。在MFC的基础上，ZHOU等[13]利用速度环的输入和输出变量建立了超局部控制模型，提出了超局部无模型和无差拍预测控制方法，仿真和实验均证明了该方法有较强的抗干扰能力，能够有效提高模型的鲁棒性。此外，文献[14-15]建立超局部无模型控制模型，利用参数辨识方法对扰动进行在线估计和前馈补偿，在一定程度上降低了电流纹波，系统动态响应性能得到了提升。在传统的无模型控制中，为了对具有参数不确定性的非线性系统进行无模型控制，常利用代数法对系统总扰动进行在线估计，估计值的精度与系统采样时间和采样数目密切相关，计算复杂且耗时[16]。

鉴于代数法对扰动进行估计的过程复杂且耗时，引入自抗扰控制(Active Disturbance Rejection Control，ADRC)[17]。ADRC将系统扰动进一步分为内扰和外扰两部分，通过扩张状态观测器(Extended State Observer，ESO)的在线估计对扰动进行补偿。文献[18]将无模型控制与扩张状态观测器设计相结合，架构出基于ESO的无模型控制的表贴式PMSM驱动系统，仿真实验证明了该控制方案的可行性和有效性。但ADRC的多参数整定在实际中实现困难。GAO[19]提出的基于线性扩张状态观测器(Linear Extended State Observer，LESO)的线性自抗扰控制器，有效减少了待整定参数数目，大大简化了ADRC的设计。

本文作者以表贴式PMSM系统的电流环控制为研究对象，创新地提出了一种基于线性扩张状态观测器的PMSM无模型无差拍电流预测控制方法(MFDPCC)。该方法充分结合无差拍预测控制和无模型控制的优点，针对传统无模型控制中基于代数法对扰动进行估计的方法计算复杂和耗时问题，利用LESO对电流环超局部模型中的已知扰动和未知扰动进行估计，降低估计过程的复杂性，在电机参数发生突变的同时，实现对交直轴电流、电磁转矩及转速给定值的有效跟踪。

1 永磁伺服系统模型

PMSM是一个高阶、非线性和强耦合的被控对象，文中为突出主要问题，建立它在dq坐标系下的定子电压方程为

(1)

式中：R0为定子电阻；ud为直轴电压；id为直轴电流；Ld=Lq=L0为交直轴电感；uq为交轴电压；iq为交轴电流；ωe为电角速度；ψf0为永磁体磁链。

考虑电机参数漂移及未建模动态的影响时，可得实际定子电压方程为

(2)

式中：Δud、Δuq分别为由电机参数漂移和未建模动态引起的不确定量，具体表达式为

(3)

其中：ΔR0=R-R0、ΔL=L-L0、Δψf=ψf-ψf0(带下标“0”的为电机铭牌上的标称值，不带下标“0”的为电机工作时的真实值)。则在考虑电机参数漂移的影响时，定子电流表达式为

(4)

2 无模型无差拍电流预测控制模型

2.1 PMSM的MFDPCC模型

对于一个非线性的一阶单输入-单输出系统，建立超局部模型[7]：

(5)

式中：y为系统输出信号；F为系统已知及未知扰动之和；α为系统输入的比例因子；u为系统输入信号。

考虑电机参数漂移和未建模动态后，将数学模型改写为

(6)

(7)

式中：Fd、Fq包含了系统已知扰动及未建模动态、参数漂移等未知扰动部分，当采样时间间隔较短时可视为常数；αd、αq分别表示定子交直轴电压的比例因子，增大αd、αq会使响应加快但同时也会引起超调，需根据工况在动态响应与超调间进行平衡取舍。

为将连续时间模型转化为离散时间模型，采用前向欧拉离散法对式(7)进行离散化，离散化后的电流预测模型为

(8)

(9)

2.2 扰动项的在线估计

在第2.1节中得到了电流环的MFDPCC控制律后，需对系统扰动进行估计。传统的MFC中常采用代数法在线估计系统总扰动，计算复杂且耗时。文中现利用线性扩张状态观测器对扰动项进行观测。

针对表贴式PMSM，选择电流和总扰动为状态变量，设计d轴的LESO为

(10)

式中：z1为系统输出id的跟踪信号；z2为总扰动Fd的估计值；β1、β2为ESO增益系数；bd为控制增益。

对式(10)进行离散化得：

(11)

为使系统处于稳定状态，设LESO的带宽为ω0、特征方程的根为-ω0[19]，推导得LESO的增益系数β1、β2为

(12)

对式(11)进行z变换以判断离散状态方程的稳定性：

(13)

考虑到采样时间足够小，则离散系统的传递函数为

(14)

式中：β01=β1×Ts；β02=β2×Ts。

根据传递函数得离散系统的特征方程为

(z-1)2+β02Ts+β01z-β01=0

(15)

β02Tsω2+2(β01-β02Ts)ω+4+β02Ts-β01=0

(16)

要使得系统稳定，则应有：

(17)

同理可得q轴的LESO为

(18)

通过LESO获得Fd、Fq与id(k)、iq(k)的估计值后，可得文中提出的基于LESO的永磁同步电机无模型无差拍电流预测控制的控制律。

3 仿真实验

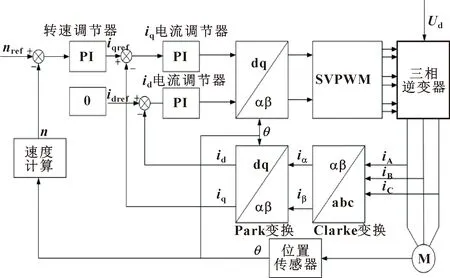
图1 基于PI控制器的电流控制

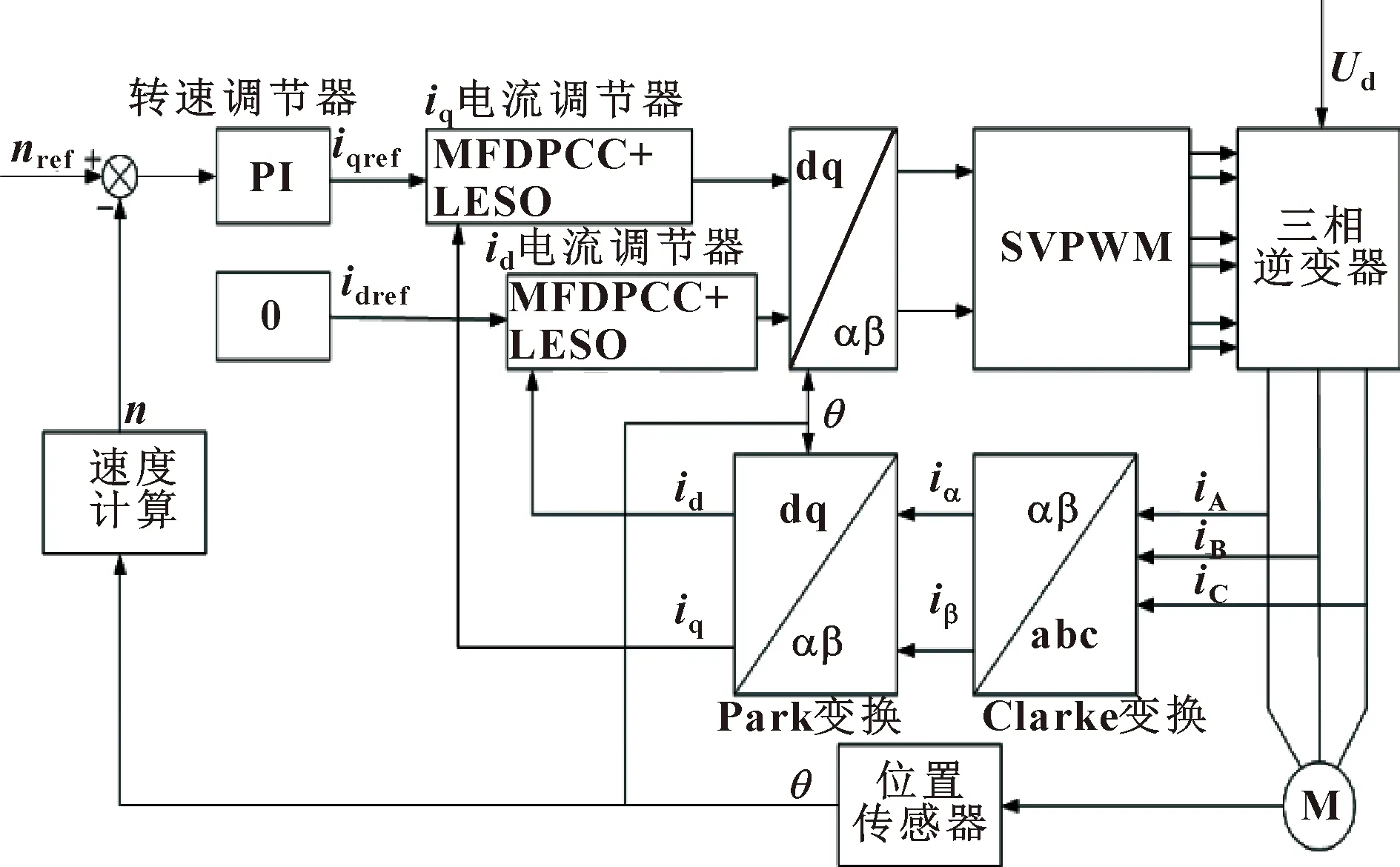
图2 基于LESO的MFDPCC控制

仿真模型中的永磁伺服系统参数标称值如表1所示。

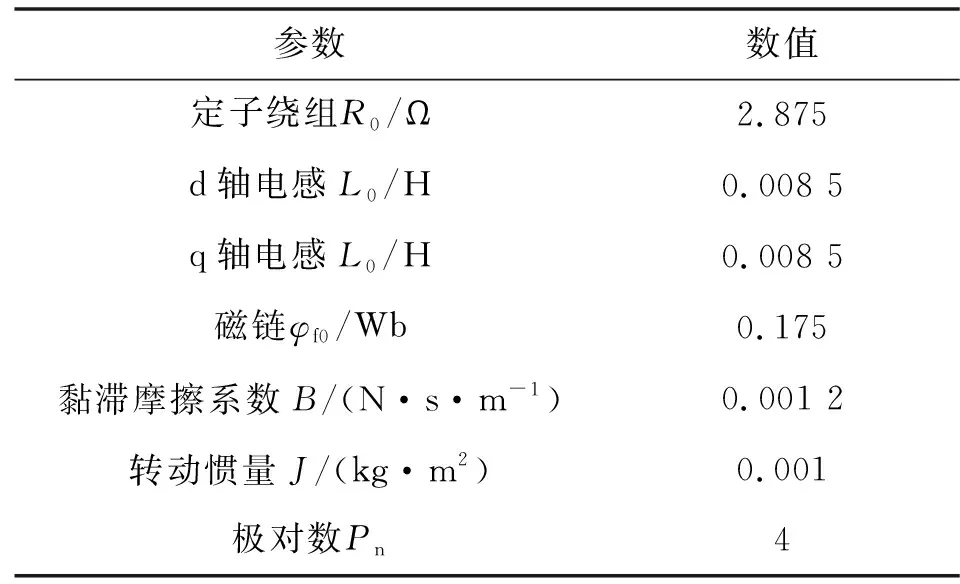
表1 参数设置

首先给定仿真条件为系统中不存在参数漂移的影响，即电机参数在运行过程中不受工况影响发生变化。给定转速指令1 000 r/mim，施加一个初始状态为0、0.1 s时突增到5 N的负载转矩TL，采样时间为2×10-7s。2种不同控制方法下的d、q轴定子电流、电磁转矩及转速的波形仿真结果如图3—图 5所示。

图 5 电磁转矩(不存在参数漂移)

观察图 3—图 5可以发现：在启动阶段和负载转矩发生突变的阶段，文中所提的控制方法下d轴电流、电磁转矩能够更好地跟踪电流和负载转矩的给定值，q轴电流能够更好地随负载转矩的变化而发生变化。

由图6可知：文中提出的控制方法在转速的响应波形中，具有更小的超调和更快的响应。为比较稳态时文中提出的控制方法与PI控制的性能，对转速响应波形图进行局部放大(图 7)，可以清晰地看到文中所提的控制方法具有更小的静差。

图6 转速(不存在参数漂移)

图7 稳定时转速的局部放大(不存在参数漂移)

其次，给定仿真条件为系统中存在电机参数不确定性，即电机的参数会受工况的影响而发生变化。设定在电机运行到0.2 s时，PMSM的参数突变为R=1.4R0、L=0.8L0、φ=0.8φf0，同时仍施加一个初始状态为0、0.1 s时突增到5 N的负载转矩，2种控制方法下的d、q轴定子电流、电磁转矩的波形仿真结果如图8—图10所示。

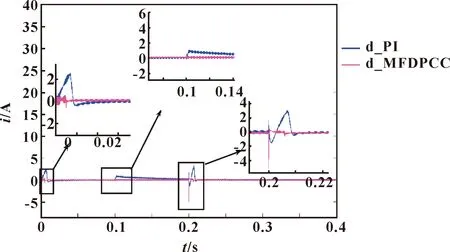
图8 d轴电流(存在参数不确定性)

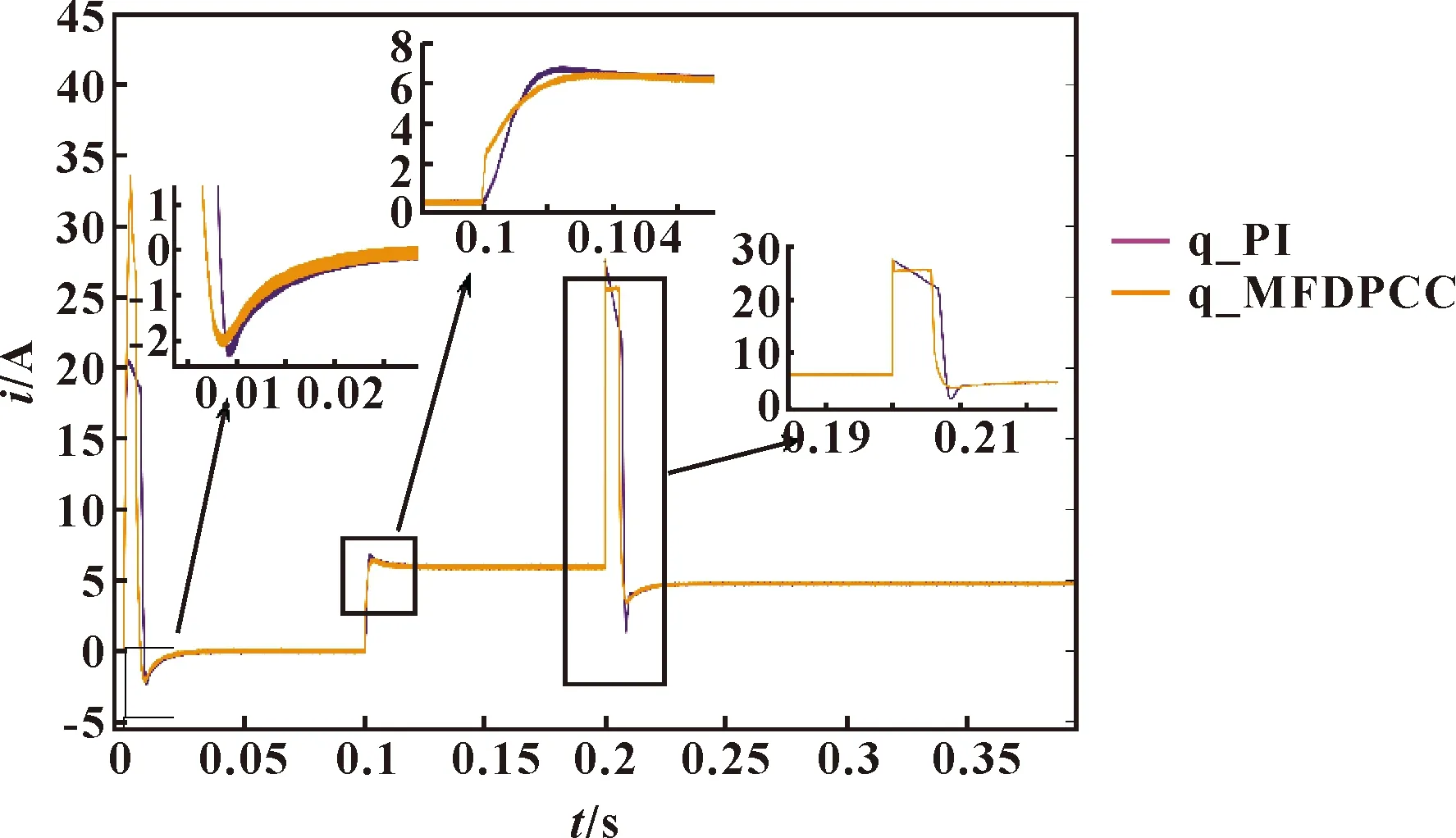
图9 q轴电流(存在参数不确定性)

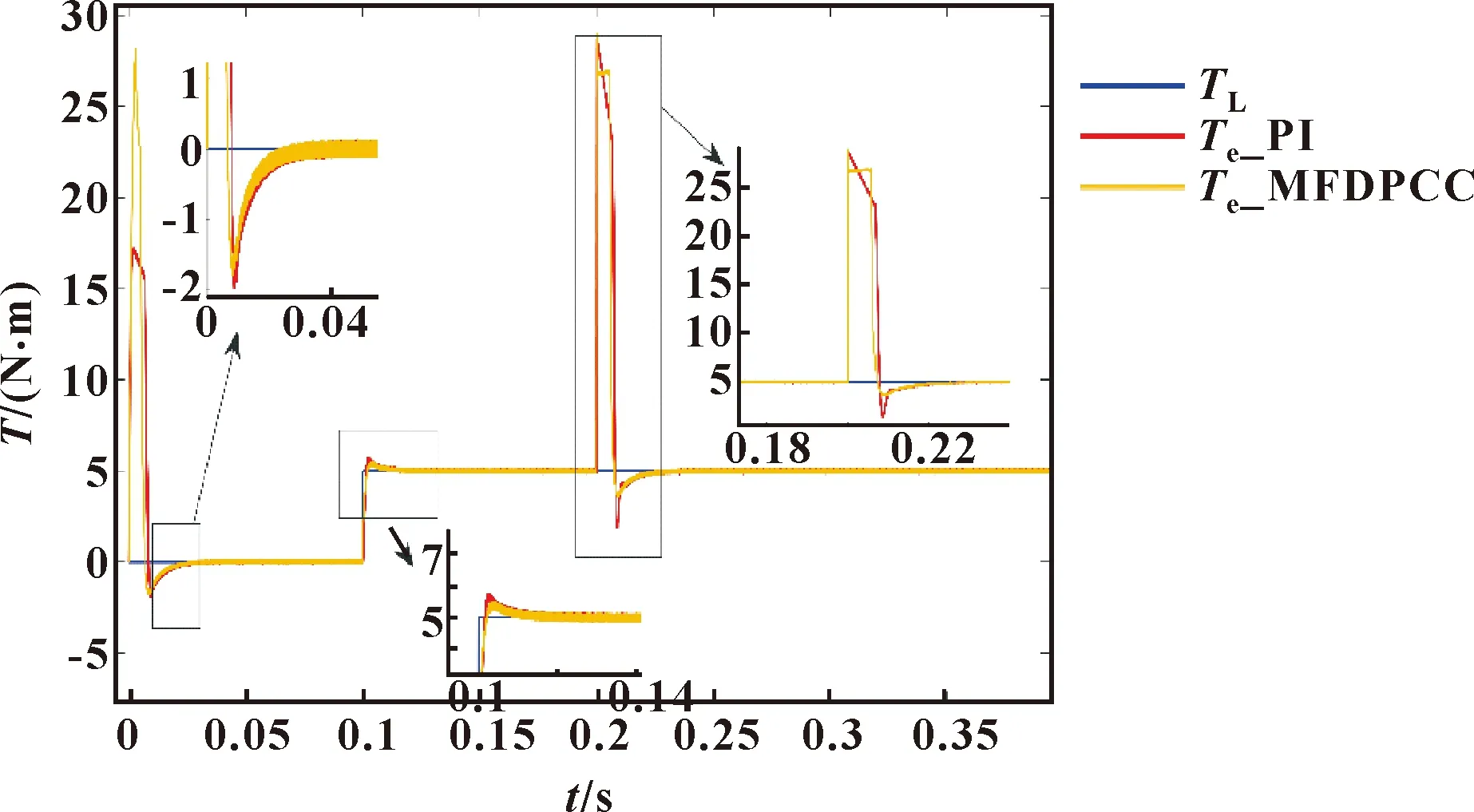
图10 电磁转矩(存在参数不确定性)

观察图8—图10可以发现：在启动阶段和负载转矩发生突变的阶段，文中所提的控制方法下d轴电流、电磁转矩能够更好地跟踪电流和负载转矩的给定值，q轴电流能够更好地随负载转矩的变化而发生变化。在0.2 s时，文中所提的控制方法能够更快克服参数变化对系统性能的影响。

由图11可知：文中提出的控制方法在转速的响应波形中，在启动、转矩突变和电机参数发生变化的瞬间皆具有更小的超调和更快的响应。为比较稳态时文中提出的控制方法与PI控制的性能，对转速响应波形图进行局部放大(图 12)，可以清晰地看到文中所提的控制方法静差更小。

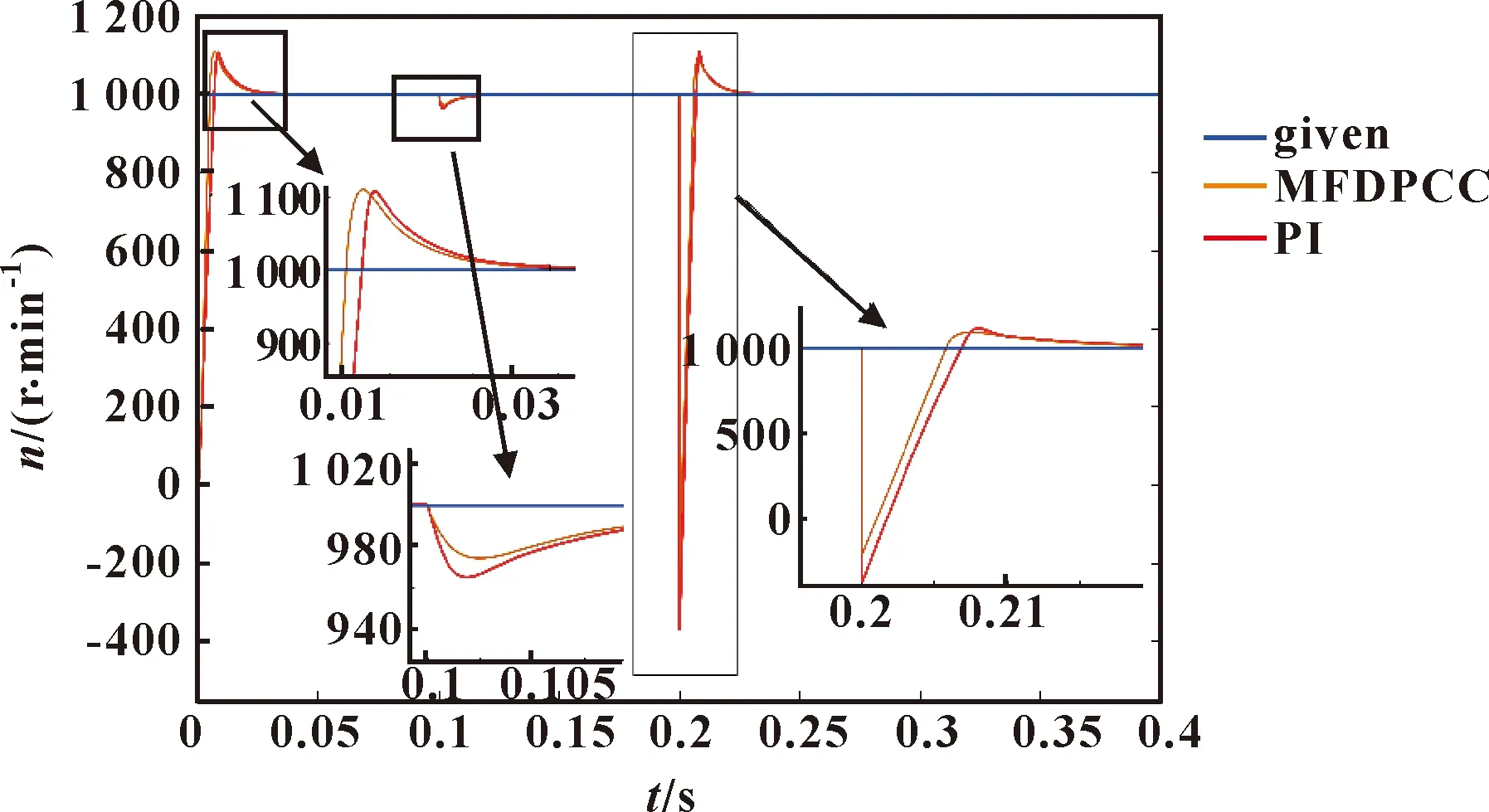
图11 转速(存在参数不确定性)

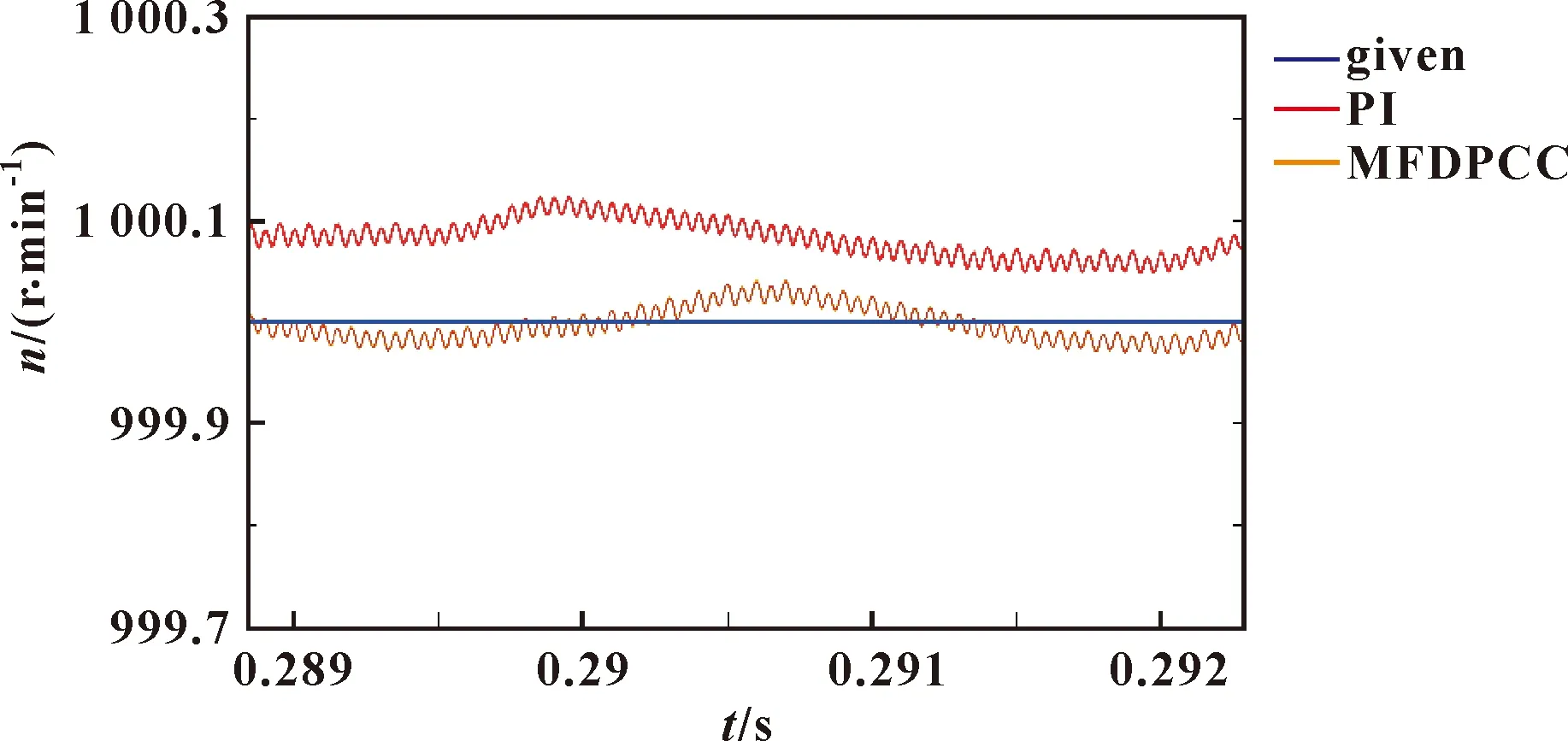
图12 稳定时转速的局部放大(存在参数不确定性)

系统仿真结果表明：所提出的基于线性扩张状态观测器的永磁同步电机无模型无差拍电流预测控制(MFDPCC)的d、q轴电子电流、电磁转矩和转速的纹波较PI控制器下的要小，能够有效消除负载突变和电机参数不确定性对系统控制性能的影响，兼具鲁棒性强的技术优势。

4 结论

文中创新性地将无差拍电流预测控制与无模型控制结合，并利用线性扩张状态观测器对电流环超局部无模型中的总扰动进行有效估计，实现了基于LESO的PMSM无模型无差拍电流预测控制，有效解决了PMSM在运行过程中电机性能受工况影响而发生变化的问题。与传统的PI控制器相比，系统仿真表明文中提出的控制方法下的d、q轴电子电流和电磁转矩纹波都较小，能够有效消除电机参数漂移和未建模动态对系统电流控制的影响，有效实现快速的动态响应，有较强的鲁棒性。文中主要围绕电流环进行改进，速度环仍采用传统的比例积分控制器，在后续的研究中，可针对速度环动态性能和稳态性能进行控制方法上的改进。