变胞手爪攀爬机器人多姿态力学分析
2023-07-27侯月阳
王 昆,侯 宇,2,孙 伟,2,侯月阳
(1.武汉科技大学冶金装备及其控制教育部重点实验室,湖北 武汉 430081;2.武汉科技大学机器人与智能系统研究院,湖北 武汉 430081)
1 引言
在钢铁、化工企业中,大量采用管道输送高温、高压、剧毒等流体介质。由于管道结构复杂、现场环境恶劣,在对管道进行检测和维护时危险系数高,容易发生安全事故。因此,研制出一种具有多姿态、能适应各种管道的攀爬机器人,对于满足实际应用具有非常重要的意义。
目前,管外攀爬机器人主要分为气动蠕动式、轮式、关节式和蛇形这几种类型。
文献[1]提出一种气动蠕动式管外爬行机器人,特点是整体结构简单,稳定性好,易于操作,但是越障能力不足且爬升高度受供气管长度的限制;文献[2]研制的轮式爬升机器人,特点是具有较高的机动性,运动稳定,但是适用范围较小,仅适用于直管;文献[3]研制的双手爪式模块化仿生攀爬机器人,特点是机构灵活性高,可适应性较强,能够跨越管道间的常见障碍,但是结构较复杂,对控制系统要求较高;文献[4]提出一种蛇形攀爬机器(CSR),特点是机器人有较好的越障性能,但负载能力存在不足。
为解决攀爬机器人负载和越障能力之间的矛盾,设计出一种变胞手爪攀爬机器人,在保证机器人整体灵活性的同时,机械手爪在夹紧过程中能自动适应管道直径和形状的变化,可以在L、T型管道上进行攀爬,能够跨越管道上的一般障碍物,并具有较好的负载能力,能够携带装置进行管道的检测和维护工作。
2 变胞手爪攀爬机器人结构设计
机器人变胞手爪机构简图及总体结构,如图1所示。攀爬机器人的总体结构包括上躯体、腰部、下躯体、上肢和下肢。各部位的连接方式,如图1(b)所示。
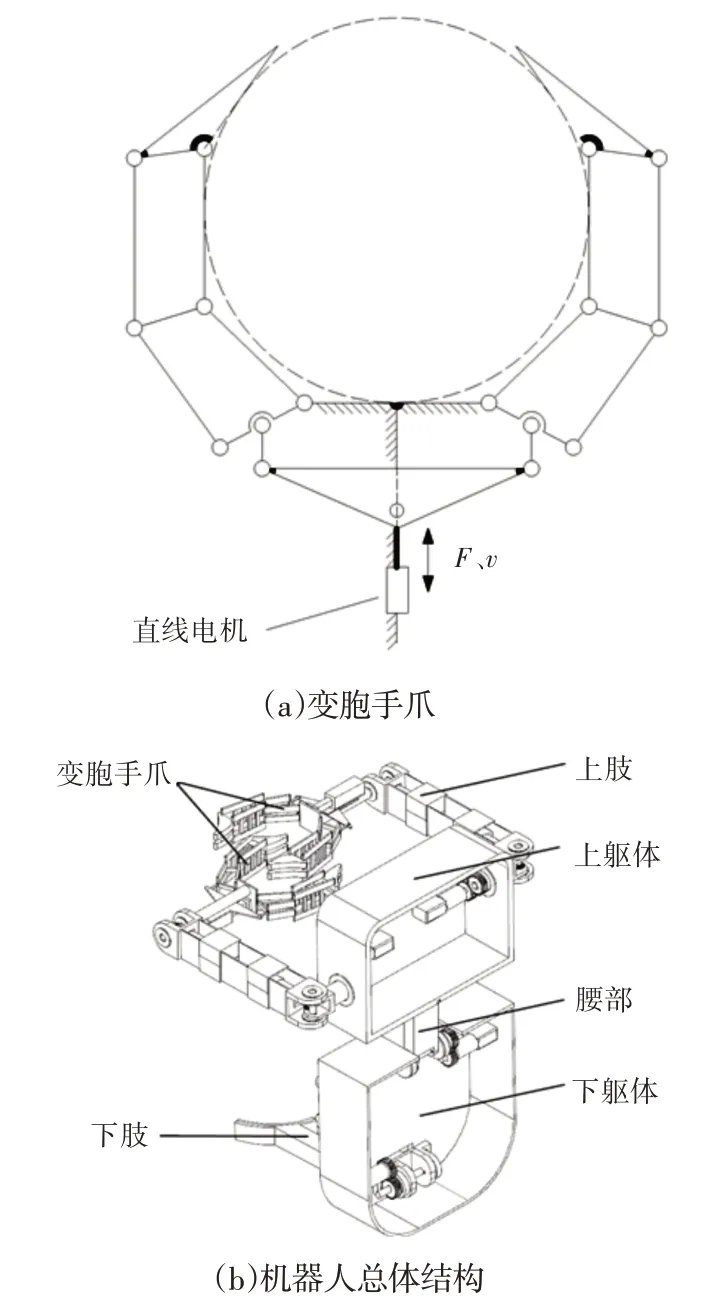
图1 攀爬机器人结构图Fig.1 Structure of Climbing Robot
攀爬机器人的整体结构是根据灵长类动物的攀爬姿势进行设计的,通过观察灵长类动物攀爬方式,我们发现灵长类动物是用两只手臂抱紧树干,下肢蹬住树干,双手交替向上攀爬。
攀爬机器人的整体结构与灵长类动物相似,其中上肢模拟灵长类动物的两只手臂,具有三个自由度,可以模拟手臂交替向上攀爬。手臂上的变胞手爪用来夹紧管道。机器人下肢模拟灵长类动物的下肢,蹬住管道,设计成这种结构简单的Y型结构,既能在腰部关节的帮助下进行辅助攀爬,也能有效的简化整体结构达到设计目的。
其中攀爬机器人的手爪采用变胞机构,变胞机构是一种能在瞬时使某些构件发生合并/分离、或出现几何奇异,并使机构有效构件数或自由度数发生变化,从而产生新构型的机构。机器人手指部分采用被动变胞的原理,当手指接触到管道之后,其中一个杆被固定,改变整个手爪的自由度,从而实现自适应抓紧。同时符合阻力最小原理,使整个手爪的适应性更强。在刚性手指外增设橡胶,以增大手指与管道之间的摩擦。同一只手爪抓取不同直径和不规则形状的管道夹紧示意图,如图2所示。
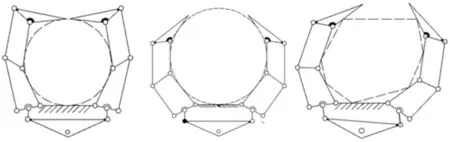
图2 手爪夹紧不同管道示意图Fig.2 Schematic Diagram of Gripper Clamping of Different Pipes
3 攀爬机器人多姿态力学分析
3.1 圆形管道攀爬力学分析
首先分析变胞手爪机构的力学特性,利用虚功原理建立变胞手爪在抓取管道时各个手指和管道的接触力与手爪驱动力之间的力学关系模型,如图3所示。

图3 手爪夹紧示意图Fig.3 Schematic Diagram of Gripper Clamping
根据虚功原理,对于具有理想约束的质点系,其平衡的充要条件是作用在质点系的所有主动力在任何虚位移中所作用的虚功和等于0,即:
式中:F1、F2、F3、F4—变胞手爪与管道的接触点产生的力;F—变胞手爪的驱动力;δ1、δ2、δ3—接触点在接触力F1、F2、F3的作用下产生的虚位移;δ—驱动力F作用下产生的虚位移,如图3所示。有:
δ1=d1φ1
δ2=d2φ2+a1φ1cos(α5-α2)
δ3=d3φ3+a2φ2cos( )γ+α8-α5+a1φ1cos(γ+α8-α5)
将δ1、δ2、δ3带入式(1),公式可变形为:
式中:αi( )
i= 1,2,…,8 —图中对应杆相对水平方向的位置角;ai、bi、ci、li( )
i= 1,2,3 —图中变胞手爪对应关节杆长;φi( )
i= 1,2,3 —每个手指的虚转角;d1—接触力F1到转轴A的距离;d2—接触力F2到转轴C的距离;d3—接触力F3到转轴E的距离;β—杆GI与竖直方向的夹角;γ—指尖的固定角。
可以得到α8、α5、α6之间的关系:
同理在四边形ABCD中可以得到α6、α2、α3之间的关系:
在三角形GHI中,可以得到α3、α1、l1之间的关系:
式中:α8、α5、α2的虚转角—φ3、φ2、φ1;δ—l1的虚位移。利用变分法可得到:
O=l3d1d2sinα1sin(α7-α8)
P=l3a2d2sinα1sin(α5-α7)
Q=l3a1b1sinα1sin(α2-α4)sin(α7-α6)
R=b1b2sin(α3-α1)sin(α7-α6)sin(α4-α3)
联立式(2)、式(3)可以得到F1、F2、F3与F之间的关系:
M1=Ta2d2cos(γ+α8-α6-α3)
M2=a2(Td1-Hd2)cos(γ+α8-α5)
M3=a2d1d2cos(γ+α8-α5)-d22d3
N1=S[a2d1cos(γ+α8-α5)-d2d3]
N2=a1cos(γ+α8-α2)(Td1-Hd2)
N3=a1cos(α5-α2)[a2d1cos(γ+α8-α5)-d2d3]
Z=a2d1cos(γ+α8-α5)-d2d3
机器人在圆形直管上攀爬步态,如图4所示。机器人利用手爪与管道之间的静摩擦力来保证机器人的稳定攀爬。
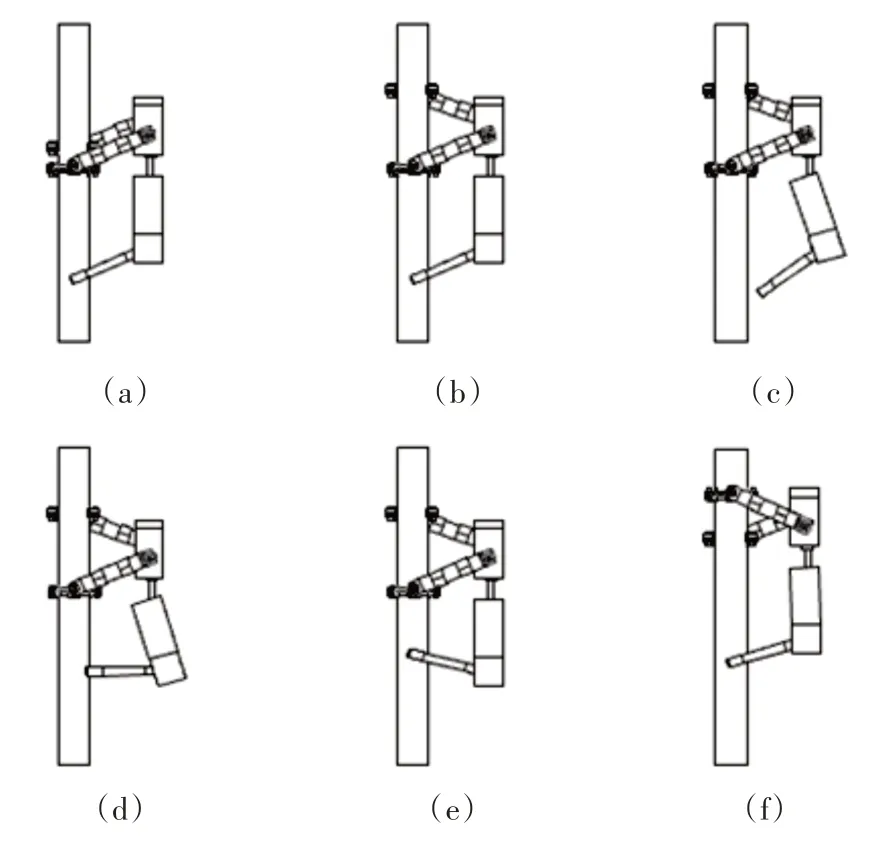
图4 机器人直管攀爬步态图Fig.4 Schematic Diagram of the Robot Straight Pipe Climbing Gait
对图4进行分析,攀爬机器人在圆形直管上攀爬时,对变胞手爪进行受力分析,即受力平衡方程式为:
式中:G—攀爬机器人的总重力为80N;μ—橡胶与钢管之间的静摩擦系数(μ取0.8);f—管道对手爪的理论最大静摩擦力;Ft—手爪对管道的总接触力。
根据静力平衡,计算出F1、F2、F3,可以计算出接触力F4。
根据设计参数,变胞手爪各杆长取值为:a1=45mm,a2=50mm,a3=40mm,b1=26mm,b2=22mm,b3=23mm,d1= 30mm,d2= 15mm,d3= 35mm,l2= 12mm;取管道直径为100mm;驱动力F= 100N。
根据以上数据可计算得到手爪夹持圆形管道各关节的接触力大小为:
F1= 35.217N,F2= 15.044N,
F3= 25.080N,F4= 27.082N
根据式(5),可以算出手爪对管道的最大静摩擦力为142.210N,且大于攀爬机器人总重力,表明机器人能够实现可靠夹持。
3.2 不规则管道攀爬力学分析
攀爬机器人在不规则管道上进行攀爬时,要保证机器人的稳定性,受力分析与圆管上攀爬一样,区别在于变胞手爪和管道的接触点不一样。且接触力的大小也不是对称的,将另一侧的接触力用Fi
‘表示,即受力平衡方程为:
同理,利用虚功原理计算出F1、F2、F3、F4、F1'、F2'、F3'与接触力F之间的关系,计算方式与上述方法一致,其中夹紧状态下的αi、di根据实际夹紧状态取值不同。
得到手爪夹持不规则管道各关节的接触力大小为:
F1= 39.364N,F1'= 29.249N
F2= 19.487N,F2'= 15.572N
F3= 30.823N,F3'= 27.336N
F4= 24.862N
根据式(6),可以算出手爪对管道的最大静摩擦力为126.696N,且大于攀爬机器人总重力,机器人能够实现可靠夹持。
3.3 L型管道攀爬力学分析
机器人在L型管道攀爬步态,如图5所示。机器人跨越L管道时,左右端手爪交替夹紧横管,并在后足的作用下将整个躯干移动到横管上。

图5 机器人越L管道步态图Fig.5 Schematic Diagram of the Robot Gait Across the L-Shaped Pipe
在图5中可以得知,当机器人跨过L型管道之后,在步态b~c的过程中手爪受力最大。手爪夹紧横管示意图,如图6所示。对机器人的手爪进行受力分析,可知,变胞手爪在横管上竖直方向的夹紧力为:
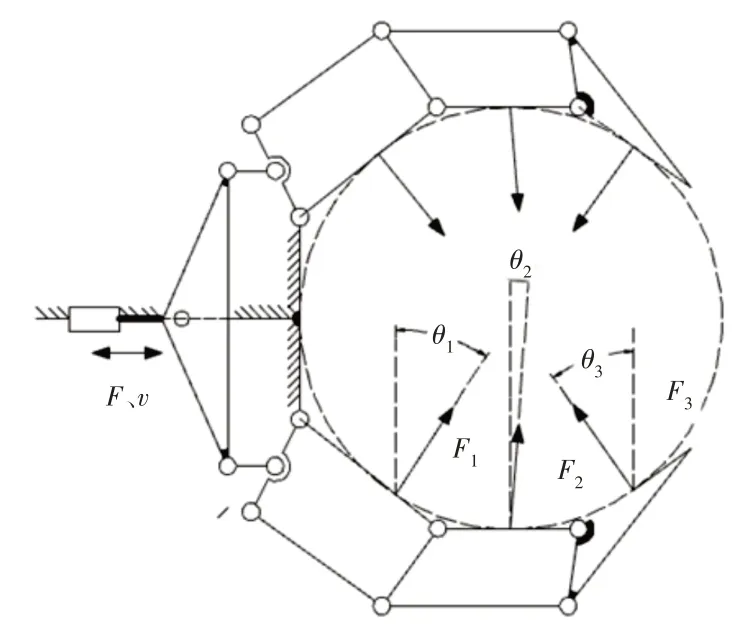
图6 横管夹紧示意图Fig.6 Schematic Diagram of Clamping Transverse Pipe
式中:θi—接触力Fi与竖直方向的夹角。
代入数据计算,变胞手爪在横管上夹紧力为104.178N,且大于攀爬机器人总重力,机器人能够实现可靠夹持。
4 机器人攀爬运动过程仿真与分析
4.1 机器人手爪夹持运动
将变胞手爪夹持圆管的三维模型导入到Adams中,对零件添加材料属性、对应的运动副、碰撞条件以及驱动信息,在驱动力为100N 的作用之下,其仿真动作及各接触力大小,如图7、图8所示。

图7 手爪夹持示意图Fig.7 Schematic Diagram of Gripper Holding
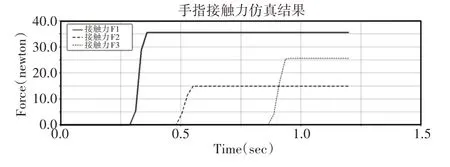
图8 变胞手爪各手指接触力Fig.8 The Contact Force of Each Finger of the Metamorphic Grippers
由图7可以看出,变胞手爪能实现适应性夹紧,证明方案的可行性,在图8中,根据仿真结果图8可知,变胞手爪各手指与管道的接触力F1=35.58N,F2=14.95N,F3=25.62N,与理论计算结果误差较小,证明方案理论模型的正确性。
4.2 机器人直管攀爬运动
在直管上,机器人实现攀爬运动,其仿真动作,如图9所示。

图9 机器人直管攀爬运动过程Fig.9 The Process of the Robot Climbing the Straight Pipe
由图9可以看出,机器人在Adams中的攀爬步态与原设计步态是一致的,模拟仿灵长类动物的攀爬步态,实现了整个向上攀爬的姿态,验证了此套方案可行性与正确性。
在图10 中,force 1 为机器人右手爪与管道之间的摩擦力;force2为左手爪与管道之间的摩擦力;force3为两只手爪总摩擦力。攀爬机械人左手爪在(0~2)s内处于夹住竖管状态,在(2~5)s时向直管上方移动,在(5~13)s内一直处于夹紧竖管状态。攀爬机器人右手爪在(0~9)s一直处于夹紧竖管状态,在(9~12)s时向直管上方移动,在(12~13)s时处于夹紧竖管状态。在整个攀爬过程中,攀爬机器人所有手爪与管道间的总摩擦力最小为82.6N,大于机器人重力80N,小于理论最大静摩擦力142.210N,可以使机器人在竖直管道上进行攀爬。
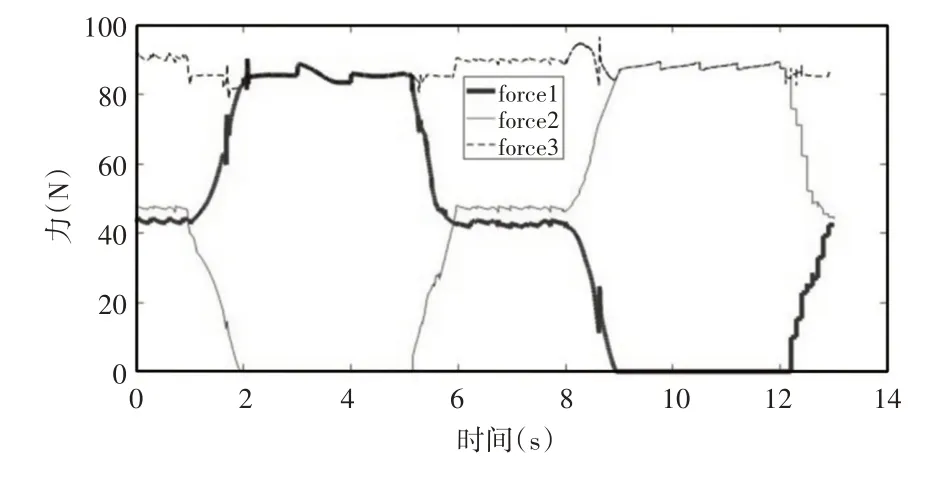
图10 手爪与管道间的摩擦力Fig.10 The Frictional Force Between the Gripper and the Pipe
4.3 机器人L型管道攀爬运动
在L型管道上,机器人实现翻转运动时,其仿真运动,如图11所示。由图11可以看出,攀爬机器人可以跨越L型管道或者其它类似的交叉管道,验证了此套攀爬方案可行性。

图11 机器人L型管道翻转运动过程Fig.11 The Process of the Robot Moving Over the L-Shaped Pipe
在图12中,force1表示右手爪与横管的接触力,force2表示左手爪与横管的接触力。攀爬机器人左手爪在(0~5)s时由夹紧竖管状态移动到横管上;在(5~12)s时,处于夹紧横管状态。攀爬机器人右手爪在(0~9)s时由夹紧竖管状态移动到横管上;在(9~12)s中处于夹紧横管状。在(5~9)s时,机器人由一只手爪与管道进行夹紧,此时手爪总夹紧力最小,为94.8N,大于攀爬机器人总重力80N,满足可靠夹持条件,且在双手爪完全夹紧之后,每个手爪的夹紧力为102.6N,与理论计算结果基本一致,证明攀爬机器人在多姿态下具有可靠夹持能力和稳定运动能力。

图12 手爪与横管竖直方向接触力Fig.12 The Vertical Contact Force Between the Claw and the Transverse Tube
5 结论
(1)变胞手爪攀爬机器人,通过手指机构的变胞,能稳定夹持不同形状的管道,相比传统的关节式攀爬机器人,具有良好的适应能力与负载能力,从而能更方便在管道上展开工作。
(2)建立了变胞手爪夹持圆形直管、不规则直管以及L型管道的力学模型,利用虚功原理建立手爪接触力和驱动力的力学模型,从而计算出机器人攀爬时,变胞手爪与竖直管道之间的理论最大静摩擦力和变胞手爪对横管的夹紧力。
(3)在ADAMS 中对机器人攀爬不同管道过程进行仿真分析,根据仿真数据与力学模型计算结果进行对比,在爬直管时,手爪和管道之间的摩擦力大于机器人自身重力,能使机器人完成直管攀爬;在机器人跨越L管道时,手爪对横管的接触力大于机器人总重力,能保证机器人实现从竖管跨越到横管上。仿真结果验证了模型的正确性,证明了机器人多姿态的攀爬性能良好。
