横纵向位移激励下变长度梁的动力学分析

刘冠男，胡振东

（同济大学航空航天与力学学院，上海 200092）

1 引言

在深井、核电站等大型建筑中，存在竖直放置的变长度操作杆，用于实现状态控制、信号传输等功能。在对该类结构进行抗震设计时，除了要检验结构的强度，还需要考虑结构的变形，变形过大则可能影响功能实现，甚至产生碰撞。在地震作用下，变长度操作杆固定于地面的顶端会随地面移动并引发结构振动，这一过程可以简化为轴向运动变长度悬臂梁在位移激励下的振动。

关于轴向运动变长度梁的研究主要集中于横向自由振动与稳定性分析。文献［1-3］利用广义Hamilton原理和假设模态法研究了轴向运动Euler梁、Timoshenko梁、粘弹性梁的自由振动特性。文献［4-6］以机械臂、航天器天线等结构为原型，对变长度梁模型进行了动力学和稳定性分析。文献［7-8］利用Euler梁理论，分别对均匀变长度梁与自由端带有主动振子的变长度梁进行了振动控制的研究。文献［9］研究了功能梯度材料变长度悬臂梁模型的动力响应。文献［10-12］将火炮系统简化为移动质量作用下的变长度悬臂梁模型，建立了横向振动方程并近似求解出振动响应。这些研究没有考虑到外激励的作用，而外激励作用下动力学分析的研究对象通常是定长度梁。文献［13］研究了基础激励作用下轴向运动定长度悬臂梁的振动及稳定性问题。文献［14-16］运用复模态法、多尺度法等方法研究了轴向运动简支梁的受迫振动。文献［17］运用节点生死方法研究了简谐激励作用下轴向运动外伸梁的横向振动特性。文献［18］研究了功能梯度梁在集中移动谐波荷载作用下的自由振动和强迫振动。这些研究考虑了轴向运动对振动的影响，但没有考虑梁长度变化对振动的影响。目前关于轴向运动梁的动力学研究中，同时考虑梁时变长度与外激励作用的研究较少，且往往只关注于横向方向的振动。

在以往该类研究的基础上，以变长度操作杆为研究对象，建立了变长度梁在横向与纵向位移作用下的动力学方程，并通过数值仿真方法近似求解出变长度梁在简谐波与地震波作用下的振动响应。结果说明了在对变长度梁结构进行抗震分析时，考虑结构时变性的影响是必要的。

采用的方法与算法为轴向运动梁动力学分析的研究补充了同时考虑梁长度变化与横纵两个方向位移激励的内容，为工程应用中相似时变结构的抗震分析提供了参考。

2 变长度梁的振动方程

将变长度操作杆简化为变长度悬臂梁模型，如图1所示。设梁的横截面积为A，截面惯性矩为I，密度为ρ，弹性模量为E。梁上端处于刚性滑槽中，且与嵌入到滑槽中的齿轮啮合，梁下端为自由端。梁在齿轮的驱动下可以在滑槽内沿轴向上下滑动，设轴向运动速度为v(t) =v0+at，其中，v0是轴向初始速度，a是轴向运动的加速度，为定值。梁在轴向运动的过程中，梁的悬臂长度也随时间发生改变，设梁的初始长度为l0，则梁的长度可表示为。在上述变长度梁模型中，滑槽限制了变长度梁顶端的横向位移，齿轮限制了变长度梁顶端的纵向位移。设yg(t)为施加在顶部滑槽上的横向地震位移，设ug(t)为通过齿轮施加在变长度梁顶端的纵向地震位移。

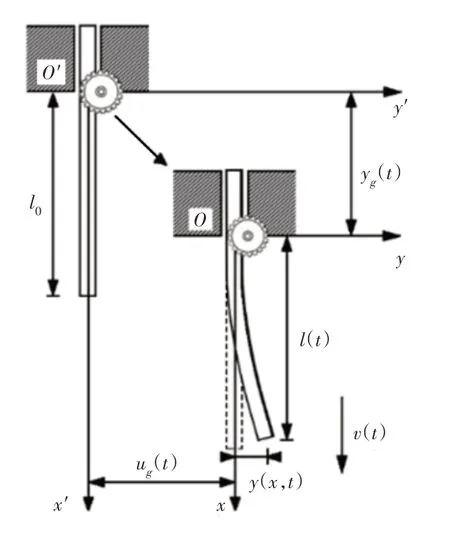
图1 变长度梁的振动力学模型Fig.1 Vibration Model of Time-Varying Beam

纵向运动包括齿轮带动及纵向位移激励作用下的刚体运动和结构自身在轴向方向的弹性变形。参考相关研究［19］可知，相同激励下，轴向运动悬臂梁的轴向振动响应要远小于横向振动响应，轴向变形引起的位移相比于横向位移可忽略不计。因此考虑在纵向方向上忽略弹性振动，采用刚体运动处理的变长度梁抗震分析简化模型。

参考支座位移激励下梁结构的动力学研究［20］，以梁顶端滑槽支承处的初始位置为原点，梁轴向向下为x'轴方向，横向为y'轴方向，建立以地面为参照的绝对坐标系O'x'y'。以梁顶端支承为原点，梁轴向向下为x轴方向，横向为y轴方向，建立以梁顶端支承为参照的相对坐标系Oxy。则梁上任意一点相对于地面的位移可表示为：

梁任意一点绝对坐标与相对坐标之间的关系可表示为：

变长度梁的动能为：

变长度梁的势能为：

式中：P(x，t) —系统的轴力，由重力加速度、相对滑槽运动的轴

向加速度与纵向地震激励加速度引起的惯性力组成，可表示为：

变长度梁外载荷所作的功W可表示为：

式中：p(t) —横向地震激励作用在滑槽的外载荷。

根据广义Hamilton原理可知：

将式（3）～式（6）代入式（7），考虑δy是任意的，可得到横纵向地震作用下变长度梁的动力学方程：

边界条件为：

3 振动方程的近似求解

变长度梁作为时变系统，其各阶模态存在时变性。采用修正后的Galerkin法求解其近似响应较为方便［21］。设描述变长度梁振动形态的振型函数为φ[x(t)]，描述时间变化的时间函数为q（t）。为方便求解，用变量ξ=x/l（t）作为振型函数中的自变量，设

式中：n—模态截断阶数。参考关于变长度梁动力响应求解的研究［1］，考虑下列两点边值问题：

该问题的频率方程与振型函数表达式如下：

式中：ki—式（13）的第i个解；

系数Ci由正交性条件确定。

各矩阵元素的表达式为：

求解系统对初始激励的响应，将初始条件按振型展开：

根据静力学方法，变长度梁初始条件下的变形可表示为：

4 数值仿真算例

为验证动力学方程的正确性，选择文献［1］的算例进行验证。令g=yg=ug= 0，线密度ρA=27kg/m，抗弯刚度EI=23300N·m2，梁的收缩速度为1m/s，梁的初始长度为7m，梁末端初始条件为。

运用Newmark-β法取前四阶模态进行计算，求解该变长度梁的振动响应。

计算结果和文献［1］算例的计算结果基本一致，由此可以验证上文所述动力学方程的正确性，如图2所示。

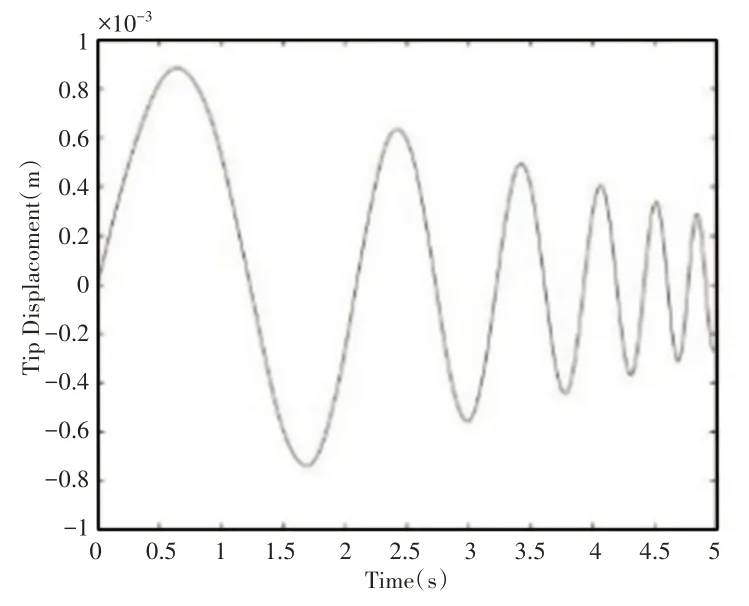
图2 l0 = 7m，v0 =-1m/s，a = 0m/s2的自由端位移Fig.2 The Tip Deflection of the Beam when l0 = 7m，v0 = —1m/s，a = 0m/s2

以某核电站变长度操作杆作为算例，参数设置为：线密度ρA=11.74 kg/m，抗弯刚度EI=70905N·m2，时变长度在（5～10）m范围内，重力加速度取为g=9.8m/s2。

为选取合适的模态数，计算变长度梁长度为5m和10m时前四阶振型的有效质量系数，如表1所示。

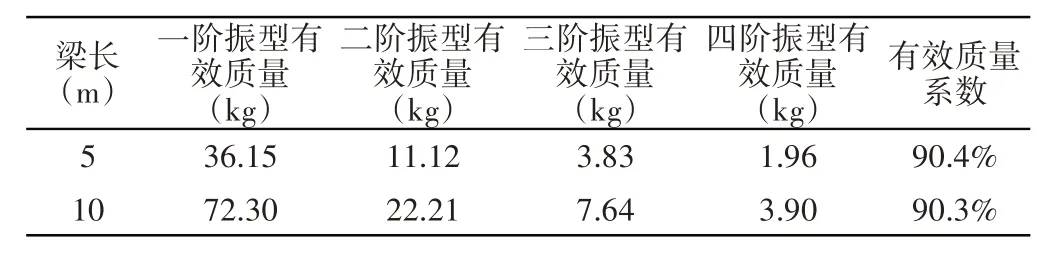
表1 变长度梁四阶振型的横向有效质量系数Tab.1 Transverse Effective Mass Coefficient of the Fourth Order Mode of the Length-Varying Beam

此时振型累计参与质量达到总质量90%，符合抗震规范的要求［22］。此外，还要保证选取到地震频率范围内的所有模态。

算例前五阶模态频率在地震频率范围内，故取前六阶模态进行计算。

为观察变长度梁的振动规律，先对变长度梁模型施加地震频谱范围内的简谐激励，设初始条件为0m/s，外激励为yg(t)=ug(t)= 0.4 sin(t)。

变长度梁在简谐激励下以不同时变速度进行轴向运动所得到的末端位移曲线，如图3～图8所示。

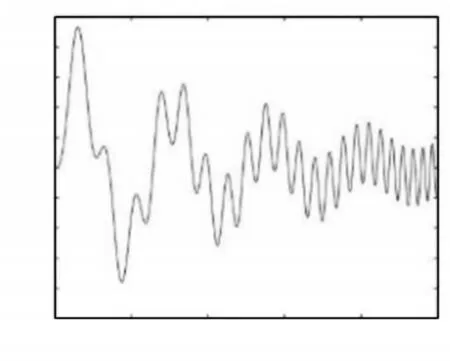
图3 l0 = 10m，v0 = —0.2m/s，a = 0m/s2的自由端位移Fig.3 The Tip Deflection of the Beam when l0 = 10m，v0 = —0.2m/s，a = 0m/s2

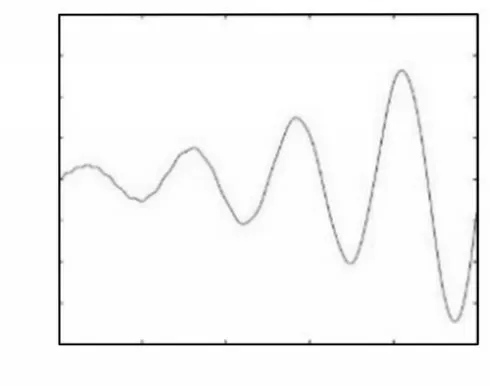
图4 l0 = 5m，v0 = 0.2m/s，a = 0m/s2的自由端位移Fig.4 The Tip Deflection of the Beam when l0 = 5m，v0 = 0.2m/s，a = 0m/s2

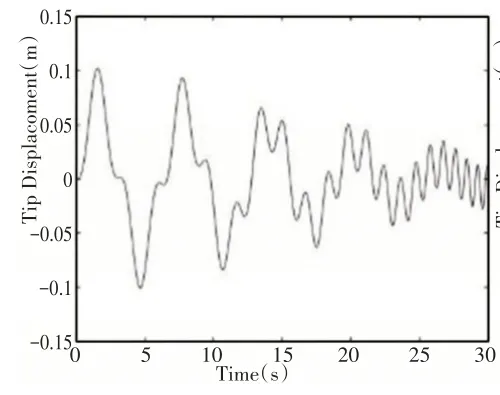
图5 l0 = 10m，v0 = 0m/s，a = —0.01 m/s2的自由端位移Fig.5 The Tip Deflection of the Beam when l0 = 10m，v0 = 0m/s，a = —0.01m/s2

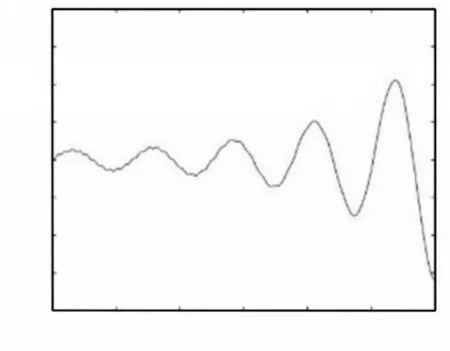
图6 l0 = 5m，v0 = 0m/s，a = 0.01 m/s2的自由端位移Fig.6 The Tip Deflection of the Beam when l0 = 5m，v0 = 0m/s，a = 0.01m/s2

图7 l0 = 10m，v0 = —0.5m/s，a = 0.025m/s2的自由端位移Fig.7 The Tip Deflection of the Beam when l0 = 10m，v0 = —0.5m/s，a = 0.025m/s2

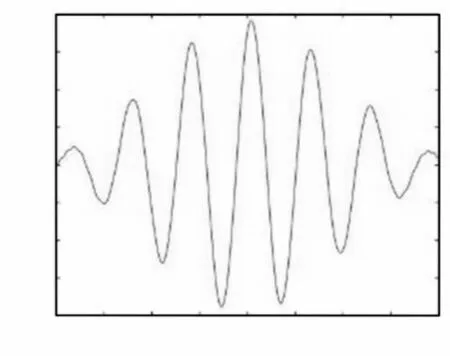
图8 l0 = 5m，v0 = 0.5m/s，a = —0.025m/s2的自由端位移Fig.8 The Tip Deflection of the Beam when l0 = 5m，v0 = 0.5m/s，a = —0.025m/s2

观察图3～图8可知，在变长度梁伸展过程中，自由端振动频率逐渐减小，而振幅逐渐增大。在变长度梁收缩时，自由端振动频率逐渐增大，而振幅逐渐减小。

接下来计算定长度梁与变长度梁在真实地震激励下的振动响应，输入的横向与纵向地震波，如图9所示。

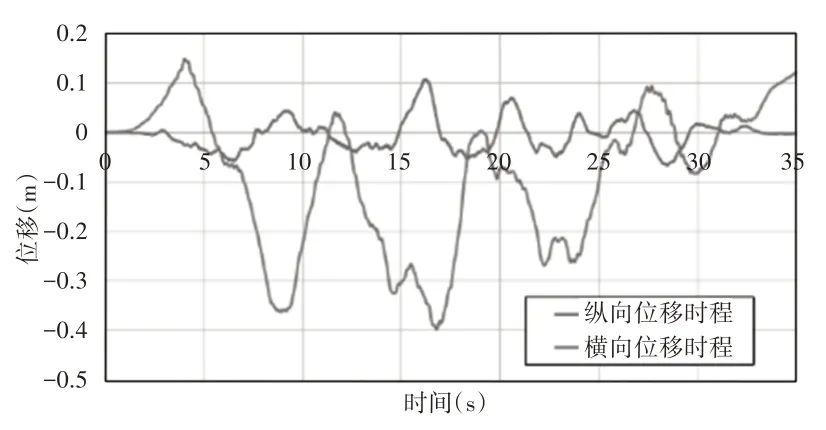
图9 横向与纵向地震位移时程曲线Fig.9 Time History Curve of Lateral and Longitudinal Seismic Displacement

定长度梁在地震激励下的末端位移曲线，如图10、图11所示。

图10 l=5m的自由端位移Fig.10 The Tip Deflection of the Beam when l=5m

图11 l=10m的自由端位移Fig.11 The Tip Deflection of the Beam when l=10m

变长度梁在地震激励下以不同时变速度进行轴向运动所得到的末端位移曲线，如图12～图17所示。

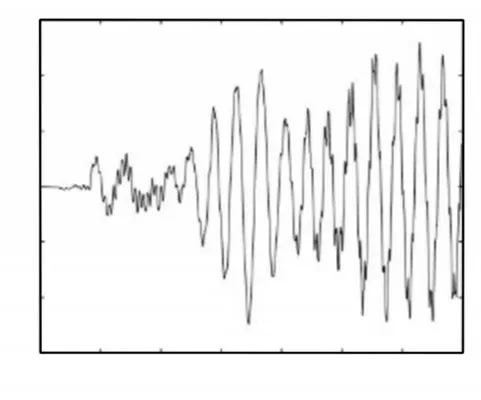
图12 l0 = 10m，v0 = —0.02m/s，a = 0m/s2的自由端位移Fig.12 The Tip Deflection of the Beam when l0 = 10m，v0 = —0.02m/s，a = 0m/s2

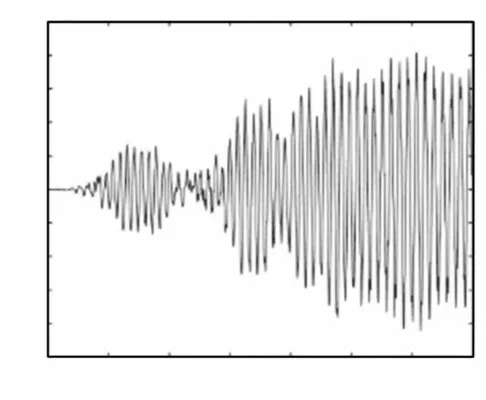
图13 l0 = 5m，v0 = 0.02m/s，a = 0m/s2的自由端位移Fig.13 The Tip Deflection of the Beam when l0 = 5m，v0 = 0.02m/s，a = 0m/s2

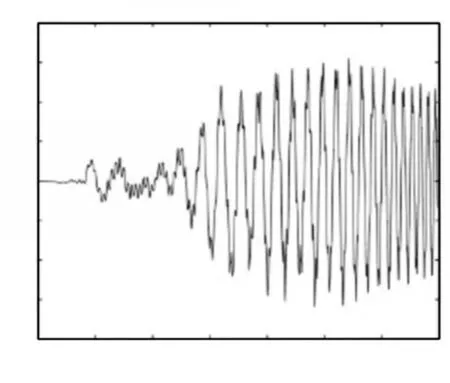
图14 l0 = 10m，v0 = 0m/s，a= —0.008m/s2的自由端位移Fig.14 The Tip Deflection of theBeam when l0 = 10m，v0 = 0m/s，a = —0.008m/s2

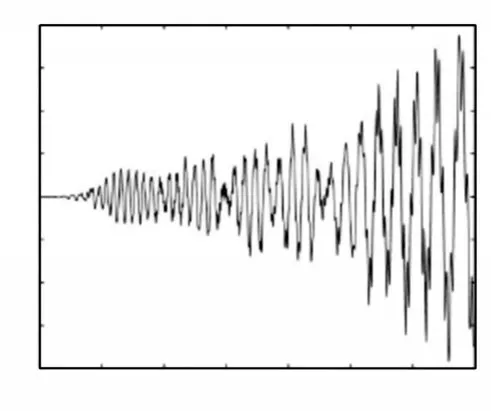
图15 l0 = 5m，v0 = 0m/s，a= 0.008m/s2的自由端位移Fig.15 The Tip Deflection of the Beam when l0 = 5m，v0 = 0m/s，a = 0.008m/s2

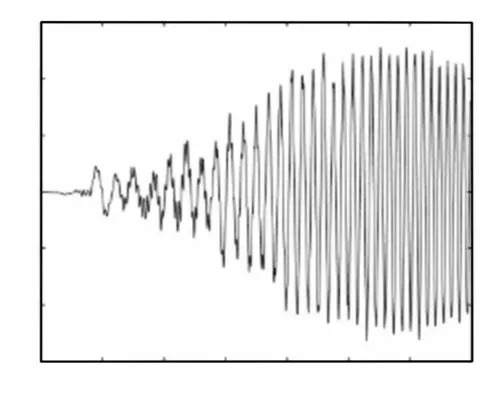
图16 l0 = 10m，v0 = —0.24m/s，a = 0.006m/s2的自由端位移Fig.16 The Tip Deflection of the Beam when l0 = 10m，v0 = —0.24m/s，a = 0.006m/s2

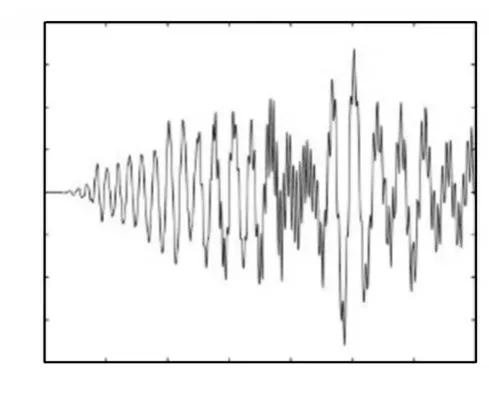
图17 l0 = 5m，v0 = 0.24m/s，a = —0.006m/s2的自由端位移Fig.17 The Tip Deflection of the Beam when l0 = 5m，v0 = 0.24m/s，a = —0.006m/s2

整理定长度梁与不同轴向运动下的变长度梁在相同地震作用下的末端最大位移结果，如表2所示。

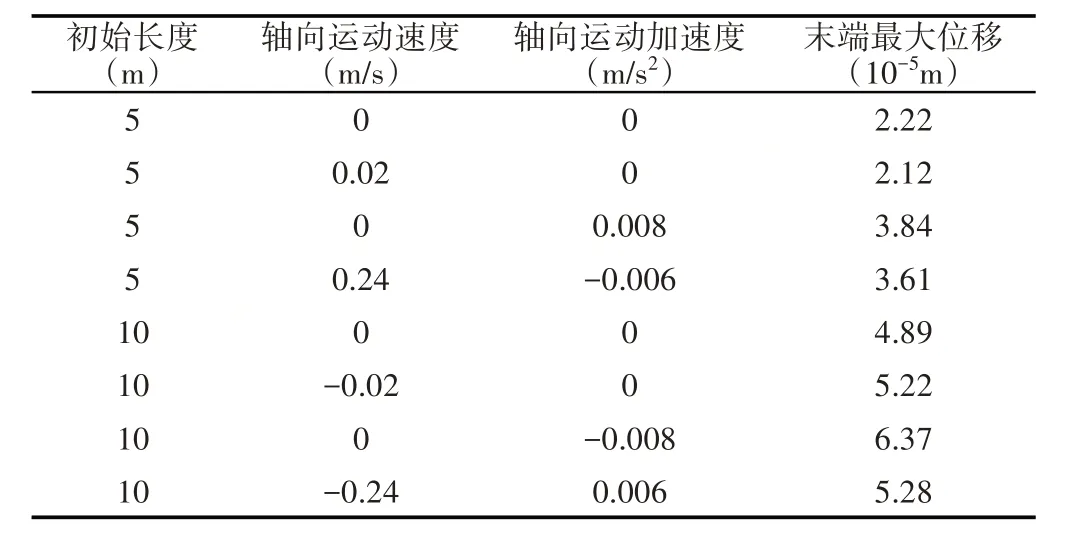
表2 梁末端最大位移Tab.2 The Maximum Tip Deflection of the Beam

根据算例的计算结果可以看出，当变长度梁在（5～10）m 范围内做轴向收缩运动时，变长度梁的地震响应大于梁长为10m和5m的固定梁的地震响应。因此，在对变长度梁进行抗震分析时，如果以固定结构代替时变结构进行计算，最终得到的结果可能小于结构真实的地震响应。

5 结论

这里以实际工程中的变长度操作杆为研究对象，提出在纵向方向上忽略弹性振动、作为刚体运动处理的抗震分析简化模型，建立了横纵向地震激励下变长度梁的时变动力学方程，并运用假设模态法和修正后Galerkin法近似求解。通过数值算例分析可知，在横纵向简谐激励下，变长度梁在轴向伸展时，振动频率减小而振幅增大，轴向收缩时，振动频率增大而振幅减小。在地震波作用下，变长度梁在收缩时，其末端最大位移大于相同长度范围内固定梁的末端最大位移。上述对比说明，用固定结构的抗震分析方法对时变结构进行抗震分析不满足保守性原则。为保证结构的安全性，在对类似具有时变性的结构进行抗震分析时，应充分考虑结构时变性的影响。