弹性连杆机构的渐变动力学及可靠性灵敏度
2023-07-27刘晓静
刘晓静
(山西工程职业学院汽车与轨道交通工程系,山西 太原 030009)
1 前言
早期,运动机构转速较低、刚性较大,因此可以忽略机构弹性变形对其工作性能的影响。然而随着现代工业的发展,机构速度高、构件质量轻的趋势使得机构呈现柔性化,导致弹性机构的弹性变形增大,使机构实际的运动偏离了预期运动。与此同时,弹性变形会产生较大的动应力,进而导致机构疲劳破坏。
因而研究弹性机构的渐变动力学及可靠性灵敏度就显得尤为重要。文献[1]最早应用伪刚体模型方法进行分析,对弹性四杆机构进行运动综合。文献[2]应用有限元分析方法探索了机构的各阶固有频率均值和转速在低阶下的关系。文献[3]则提出了机械动态与渐变可靠性理论,基于首次穿越理论的可靠性分析研究现状进行了详细的阐述。但目前国内外计算动应力的方法比较复杂[4],存在计算工作量大,工作效率低的问题。1989年,文献[5]将Kriging理论推广到确定性计算机实验的设计和分析领域,并给出了一种较实用的Kriging 算法(或Kriging 模型)。Kriging 模型根据相关函数使其具有局部估计的特点,是一种保证方差最小的无偏估计的模型,因此它受到近似确定计算机模型越来越多的青睐[6]。因此,文中采用Kriging替代模型,使其具有较好的拟合度,同时为后续计算可靠性灵敏度较大程度地降低计算量。
这里以两节点八自由度梁单元为基础,建立弹性连杆机构的动力学模型,获得具有渐变参数的系统动力学方程,进而建立Kriging近似替代模型。最后通过算例,考虑构件弹性变形求解其动力学特性和可靠性灵敏度,使计算结果更加接近工程实际。利用响应面近似替代模型可以较大程度地提高计算效率,通过修正构件参数可以优化弹性连杆机构的可靠性。
2 弹性连杆机构动力学建模
2.1 梁单元运动学关系
选取两节点八自由度等截面梁为研究对象,单元内的纵向位移(SW)和轴向位移(SV)分别满足五次Hermit多项式和线性分布,任意一点的纵向位移(SW)和轴向位移(SV)都可通过“型函数”和单元坐标系中的广义坐标表示为:
式中:u1,u5—节点轴向位移;u2,u6—节点纵向位移;u3,u7—节点弹性转角;u4,u8—节点曲率;ϕi—型函数。
这里在忽略刚柔耦合项的前提下,研究梁单元运动学关系[7]。假定机构的刚体(加)速度和弹性(加)速度的矢量和为实际(加)速度。
结合运动关系及式(1),可以得到梁单元轴线上坐标x处的速度为:
2.2 梁单元微分方程
为了得到梁单元的动力学方程,这里需要引入单元的动能、变形能和Lagrange方程[8]。
根据材料力学和式(2),分别得到单元动能和变形能的矩阵形式为:
将式(3)、式(4)代入式(5)中,整理得到梁单元运动微分方程式为:
根据机构运动学假定,式(6)可改写为:
2.3 系统微分方程
为使单元运动方程组集成系统运动方程,这里引入一组整体坐标系中的单元广义坐标[10]。
它与单元坐标系中的广义坐标列阵关系为:
式中:R—坐标转换矩阵。
将式(9)代入式(7)中,得到整体坐标系中的梁单元运动微分方程为:
定义系统广义坐标列阵为:U={U1,...,UN}T
式中:N—弹性力学分析的自由度数。
坐标协调矩阵Bi可将单元编号Uie和系统编号U实现转换,表示为:
将式(11)代入式(10)得到以系统坐标为未知量的单元运动微分方程,再将各单元对应坐标系下的运动微分方程进行叠加,得到系统运动方程为:
当考虑阻尼时,系统运行方程为:
其中,阻尼矩阵C常取比例阻尼形式,即:
式中:α、β—材料的比例系数,一般由前两阶固有频率确定。
3 弹性连杆机构渐变动力学特性
3.1 固有频率和特性
由于阻尼对机构的固有频率影响非常小,根据无阻尼自由振动方程,可以得到机构的固有频率[11]和模态。
根据机构的自由振动得到下列等式:
上式存在非零解的条件是系数矩阵行列式为0,即:由此得到特征值λ=ω2,将其代入式(15)中得到对应的特征向量(模态)X。其中X()
i对应特征值,i= 1,2,3,…,n。
3.2 动态应力应变分析
梁单元任意一点的弯曲应变为:
式中:ξ—在y方向上的坐标;S''W—单元纵向位移对于坐标x的二次导数。
梁单元中,线性单元的拉伸应变[12]为:
式中:单元轴向和纵向位移对于坐标轴变化率取平方引起的附加拉压应变。
同理求得拉压应变后,梁单元任一点的应变是弯曲应变和拉压应变的叠加,由此得到总体应变为:
矩阵;U通过u=RiBiU得到。
此过程中没有考虑剪切应变的影响,因为一般情况下这种影响是微小的,可以忽略。
根据σ=Eε,当柔顺杆件弯曲时,任意截面外边缘的弯曲应力为:
任意截面的拉压应力为:
式(22)中可以看出单元中拉压应力为常值。因此单元中外边缘任意一点的应力为:
所有截面中最大动应力的绝对值为:
任意一个位置的动应力可由式(24)得到,按公式计算可得不同时间不同位置的单元动应力。
4 弹性连杆机构的可靠性灵敏度
4.1 Kriging模型
假设给定m个样本点及其响应,y表示响应的预测值,F(β:,l,x)表示回归模型,zl(x)表示随机函数(随机过程),则响应的预测值模型[13]为:
随机部分zl(x)满足以下统计特征:
定义随机部分任意样本点间的相关方程为:
待测点与样本点的相关向量中的元素为:任意预测点x处的响应可通过样本点线性组合得到,即:
为了保证拟合的无偏差性,预测误差均值应为0、方差为极小值,进而得到系数C。
因为Fβ≅Y,则模拟的最小二乘估计为:
记残差为Rγ*=Y-Fβ,可得:
由式(31)可知,只要给定f(x),r(x)便可得到任意待测点的预测响应。
预测误差的方差为:
式中:y(x)—响应的真实值。
为保证方差最小,需要计算不确定的参数σ和相关系数R中的θ,则其对数似然函数为:
ln(P(x))
则问题转化为求解最大化无约束问题:
4.2 Kriging响应面构建中常用的试验设计方法
响应面的构造,首先是初始样本点的选取,可以通过随机采样获取,也可以通过优化试验设计进行采样,最终使初始样本点在样本空间内均匀分布,以便获得良好的近似Kriging替代模型。为了获得良好的数据,常用的试验设计方法有:全因子试验设计、部分因子试验设计、中心复合试验设计、拉丁方设计和序列探索实验设计方法等。在众多试验方法中,拉丁超立方(LHD)是使用较为广泛的方法,下面对拉丁超立方进行一个简单介绍。
假设在n维空间内抽取m个样本点,拉丁超立方抽(LDS)的步骤为:
(1)将n维中每一维划分为互不重叠的m个区间,使得每个区间有相同的概率(通常考虑到均匀分布,每个区间的长度相同)。
(2)在不同维不同区间中随机抽取一个点。
(3)再从每个区间里随机抽取(2)中选取的任一维点,并将它们组成向量,得到初始样本点。
4.3 拟合优度(决定系数)
响应面拟合结果可以通过拟合优度(决定系数)来判定。
假定Y是m个样本点的真实响应值,Y是真实响应值的均值,y是样本点通过Kriging模型得到的预测响应值。总离平方和(SST)与残差平方和(SSE)分别为:
则拟合优度:
4.4 失效概率
假定结构的功能函数为Z=gX(X),随机变量X的概率密度函数为fX(x)。按fX(x)对X进行随机抽样,所得的样本代入功能函数Z=gX(X),Z<0则记为失效一次。设模拟次数为N,其中Z<0的次数为nf次。根据概率论总的大数据定律中的Bernoulli定理[14]知,N次独立试验中的失效概率 收敛于该事件的概率nf N,pf则失效概率[14]估计值为:
结构的失效概率可以表示为:
式中:I(x)—x的指示函数。规定x<0时,I(x) = 1;x≥0,I(x) =0。根据式(39),X的第i个样本值为xi,则pf的估计值为:
4.5 可靠性灵敏度
灵敏度[15]为失效概率pf对基本变量xi的分布参数θ(k)x i(i=1,2,...,n;k= 1,2,...,m),其 中mi为第i个变量xi分布参数总数的偏导数,将失效概率的积分对分布参数θ(k)x i求导数,则得到可靠性灵敏度:
5 算例
5.1 弹性连杆机构[17]动力学分析
平面弹性连杆机构的主要参数,主动杆的转速为300r/min,如表1所示。将弹性四杆机构的模型结构,每个部件划分为4个单元,每个单元节点有4个节点广义坐标,如图1所示。
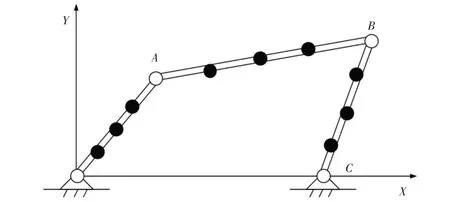
图1 弹性四杆机构模型结构Fig.1 The Module of Elastic Four-Bar Mechanism

表1 四杆机构参数Tab.1 Parameters of the Four-Bar Mechanism
在该转速下系统的前三阶固有频率,如图2所示。
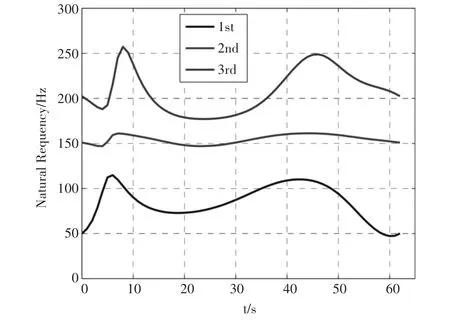
图2 系统前三阶固有频率
表示主动杆的转速分别为300r/min、600r/min和1200r/min不同时刻机构对应的最大应力,如图3所示。随着转速的增加,机构的最大动应力随之增加。
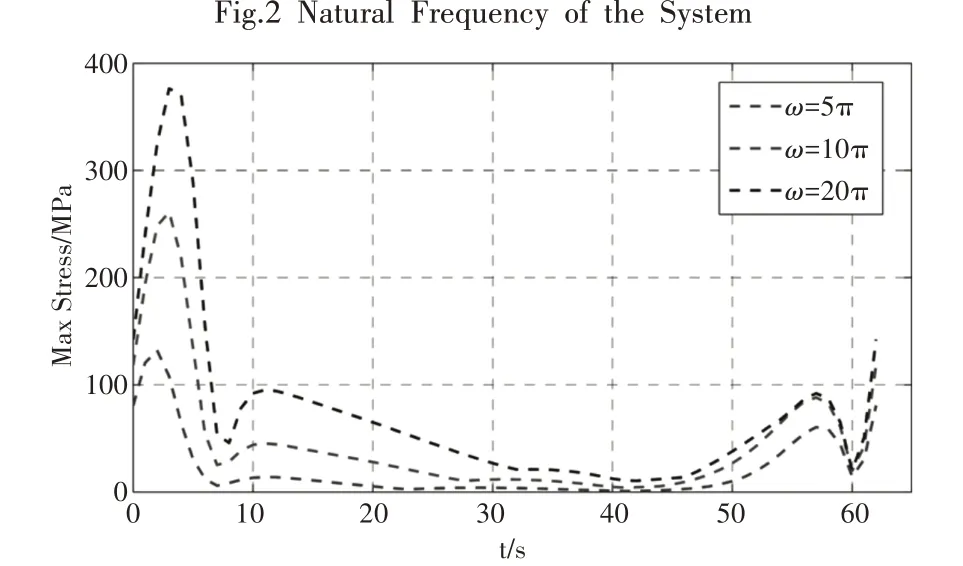
图3 系统最大动应力Fig.3 The System Maximum Dynamic Stress
5.2 弹性连杆机构的可靠性灵敏度
首先通过拉丁超立方[18]抽取50个样本点,根据动力学特性得到结构真实响应值。根据样本点及其响应建立Kriging近似替代模型。另取误差检验参考点100个。Kriging近似替代模型的预测值和真实值的拟合效果的对比,从图中可知有较好的拟合结果,同时得到拟合优度(决定系数)为:R2= 0.9852,如图4所示。

图4 Kriging模型拟合效果Fig.4 Model Fitting Effect of Kriging
主动杆转速为300r/min,在Kriging模型的基础上,利用拉丁超立方抽样方式进行抽样,设定抽样模拟次数为5000次,最大应力随着模拟次数的增加的变化曲线,如图5所示。

图5 基于Kriging模型最大应力随抽样模拟次数的变化曲线Fig.5 The Maximum Stress Changes with the Increase of the Simulation Curve
由图5可以看出:随着抽样模拟次数的增加,最大应力抽样结果趋于平稳收敛,在最大应力为261.06MPa处收敛,该图表明近似替代模型可以准确计算机构实际可靠度。
弹性连杆机构杆件尺寸存在随机性,具体参数,如表2所示。选取[-3σ,3σ]为样本采集范围。
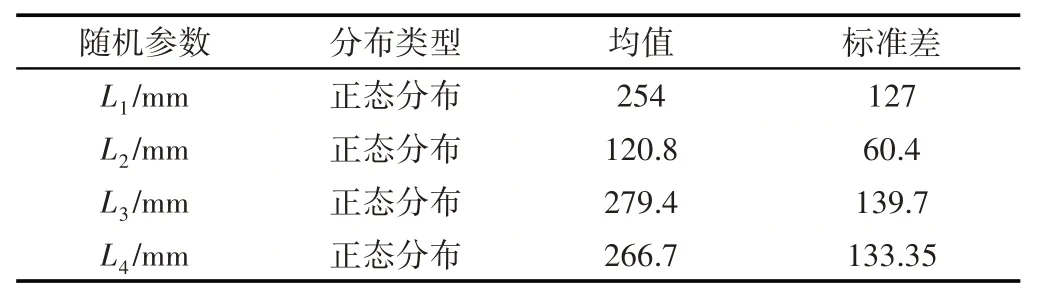
表2 机构变量参数表Tab.2 Variable Parameter List
主动杆件转速为300r/min,根据表2变量参数表利用拉丁超立方抽样1000次计算曲柄中点弹性纵向位移随着主动杆件转动的失效概率,最大的失效概率为0.427 出现在(0~60)°内,如图6所示。
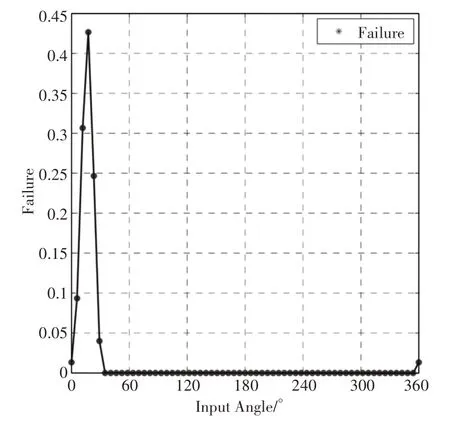
图6 曲柄中点弹性位移失效概率Fig.6 The Failure of Crank Midpoint
曲柄中点弹性纵向位移对于各杆件参数的均值可靠性灵敏度和标准差灵敏度,如图7、图8所示。由图中可以看出在同一时刻,不同参数的均值和标准差对失效概率会产生不同的影响,即灵敏度值有正有负。在不同时刻,相同参数的均值和标准差对失效概率产生相同的影响,但是对失效概率的影响程度即灵敏度值会随着主动杆件位置的改变而发生相应的改变,系统失效概率最大时各参数的灵敏度达到极值。

图7 曲柄中点弹性位移各参数的均值灵敏度Fig.7 Mean Sensitivity of Each Crank Midpoint Elastic Displacement Parameters

图8 曲柄中点弹性位移各参数的标准差灵敏度Fig.8 Standard Deviation Sensitivity of Each Crank Midpoint Elastic Displacement Parameters
灵敏度直方图,如图9、图10所示。

图9 均值灵敏度直方图Fig.9 Histogram of Mean Sensitivity
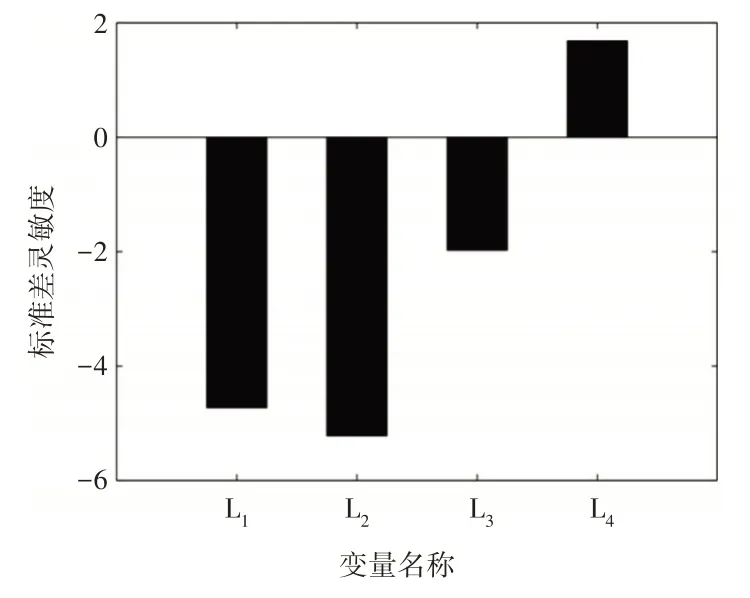
图10 标准差灵敏度直方图Fig.10 Histogram of Standard Deviation Sensitivity
从图中可以得到杆件L2的均值和标准差对系统可靠性都具有最大的影响,L2的均值灵敏度值为∂Pf/∂μ2=-25.694,标准差灵敏度值为∂Pf/∂σ2=-4.89648,由此可见灵敏度对于可靠性的影响是消极的。
而均值产生积极影响的是参数L1,标准差中产生积极影响的是参数L4。
6 结束语
(1)这里以梁单元为基础,利用广义坐标和Lagrange方程建立单元运动微分方程。通过坐标转换矩阵和协调矩阵,单元运动微分方程组集得到系统运动微分方程。利用动力学模型对弹性连杆机构的渐变动力学特性进行分析。
(2)利用拉丁超立方抽样,对比真实值和Kriging响应面近似替代模型得到的预测值,分析可知响应近似替代模型具有良好的拟合度。
因此在计算弹性连杆机构的渐变动力学和可靠性灵敏度时,基于近似替代模型,可以较大程度地提高计算效率。
(3)以平面弹性连杆机构为例,进一步证实Kriging近似替代模型具有良好的拟合度。随着主动杆转速的提高,机构任意时刻的最大动应力随之增大,因此控制机构的动应力可以通过控制主动杆件的转速实现。
(4)基于Kriging替代模型,平面弹性四杆机构曲柄中点的弹性纵向位移的失效概率最大值出现在(0~60)°内,最大的失效概率为0.427。
杆件L2的均值和标准差对系统可靠性均具有最大且消极的影响。而只有杆件L1的均值及L4的标准差对系统的可靠性产生积极影响。
