基于梯度惩罚生成对抗网络的过采样算法

陶家亮 魏国亮 宋燕 窦军 穆伟蒙

摘要：在不平衡数据分类问题中，为了更注重学习原始样本的概率密度分布，提出基于梯度惩罚 生成对抗网络的过采样算法（OGPG）。该算法首先引入生成对抗网络（GAN）， 有效地学习原始数 据的概率分布；其次，采用梯度惩罚对判别器输入项的梯度二范数进行约束，降低了 GAN 易出现 的过拟合和梯度消失，合理地生成新样本。实验部分，在 14 个公开数据集上运用k 近邻和决策树 分类器对比其他过采样算法，在评价指标上均有显著提升，并利用 Wilcoxon符号秩检验验证了该 算法与对比算法在统计学上的差异。结果表明该算法具有良好的有效性和通用性。

关键词：  不平衡数据 ；过采样算法 ；概率密度分布 ；生成对抗网络 ；梯度惩罚

中图分类号：  TP 181             文献标志码：   A

Oversampling algorithm based on gradient penalty generative adversarial network

TAO Jialiang1， WEI Guoliang2， SONG Yan3， DOU Jun3， MU Weimeng1

（1. College of Science， University of Shanghai for Science and Technology， Shanghai 200093， China;2. Business School， University of Shanghai for Science and Technology， Shanghai 200093， China;3. School of Optical-Electrical and Computer Engineering， University of Shanghai for Science and Technology， Shanghai 200093， China）

Abstract： In order to pay more attention to learning for probability density distribution of original samples in imbalanced data classification problem， an oversampling algorithm based on the gradient penalty generation adversarial network （OGPG） was proposed. Firstly， generation adversarial network （GAN） was adopted to effectively learn the probability density distribution of original data. Secondly， the gradient penalty was used to constrain the gradient two-norm of the input term of discriminator， which reduced the overfitting and gradient disappearance that appeared easily in GAN， so that the new samples were reasonably generated. In the experiment， the k-nearest neighbor and decision tree classifiers were adopted to compare the other oversampling algorithms， the evaluation indicators were significantly improved. The Wilcoxon signed-rank test was used to verify the statistical difference between this algorithm and the comparison algorithm. The results show that this algorithm has good effectiveness and generality.

Keywords：   imbalanced  data; oversampling algorithm; probability  density  distribution; GAN; gradientpenalty

不平衡數据的分类问题在数据挖掘和机器学习领域中一直倍受关注。美国人工智能协会和国际机器学习会议分别就这个问题举行了研讨会。现实生活中，很多领域都会出现数据不平衡的问题，例如金融诈骗[1]、精准医疗[2]、故障诊断[3]、人脸识别[4-5]等。

数据不平衡[6]是指数据中某些类别的样本数量远比其他类别的多。通常情况下，少数类数据中包含更多重要的信息，是研究者重点关注对象。

目前处理不平衡数据分类的方法可以分为两大类：基于算法层面[7]和基于数据层面[8]。算法层面主要包括代价敏感学习[9]和集成学习[10]：代价敏感学习通过最小化贝叶斯风险确定代价函数，以最小化误分类代价为目标，但是误分类代价的先验信息是难以获得的；集成学习是将多个分类器的分类结果结合在一起，提高集成分类器的精度，进而关注少数类的重要性。但这两类算法没有改变数据分布。数据层面主要包括欠采样技术[11]、过采样技术[12]。数据层面的技术主要通过改变样本比例，例如欠采样技术主要是通过减少多数类样本，使得多数类样本和少数类样本趋于平衡，但随机地舍弃样本可能会丢失潜在的有用信息。随机过采样方法通过随机复制少数类样本，但是该方法只是简单的复制样本，增加了过拟合的风险。目前，过采样技术的应用较为广泛，因为该技术不仅保证了数据平衡，还没有损失原始数据的有效信息。

过采样技术的研究有很多，例如 Chawla等[13] 提出了合成少数类过采样技术（synthetic minority oversampling technique， SMOTE），该算法在少数类样本中与其近邻样本之间线性插值合成新样本，没有考虑少数类样本内部的数据分布情况。He 等[14] 提出了自适应合成（adaptive synthetic， ADASYN）过采样方法，该算法通过样本点的学习难易程度给少数类样本赋予权值。此外，为了加强对边界样本的学习，边界自适应合成过采样技术[15]（B-SMOTE1， B-SMOTE2）被提出。随着深度学习的高速发展，基于网络过采样的算法应运而生， Goodfellow 等[16] 提出生成对抗网络（generative adversarial network， GAN）模型，通过生成器网络学习原始数据的分布。 Douzas 等[17]提出利用条件生成对抗网络学习原始数据的分布，再对少数类进行过采样算法。何新林等[18]提出了基于隐变量后验生成对抗网络的过采样算法（ latent posterior based GAN for oversampling，LGOS），该算法引入隐变量模型，降低了高斯噪声对生成样本的随机性影响。但 GAN 在训练过程易出现过拟合或梯度消失的风险，可以对损失函数施加惩罚项[19]，降低风险的发生。上述方法虽然在分类精度上有所提升，但没有充分考虑原始数据的分布，进而影响合成样本的安全性以及分类结果。

针对上述问题，本文提出了一种基于梯度惩罚生成对抗网络的过采样算法（ oversampling algorithm based on the gradient penalty generation adversarial network ， OGPG ）。該算法引入生成对抗网络，通过网络的生成器模型有效地学习原始数据的概率密度分布；运用梯度损失模型对生成对抗网络判别器输入项的梯度二范数进行约束，降低过拟合和梯度消失的风险；在14个公共数据集上采用两个分类器与多种算法进行了对比实验，并利用 Wilcoxon符号秩检验[20]验证了所提算法的有效性和通用性。

1 生成对抗网络模型及梯度惩罚模型

生成对抗网络（generative adversarial network， GAN）模型是一种无监督的生成模型，由生成器和判别器网络组成，能够有效地学习原始数据的概率密度分布。梯度惩罚模型是一种基于梯度损失的约束模型，降低了生成对抗网络出现过拟合和梯度消失的风险。

1.1 生成对抗网络模型

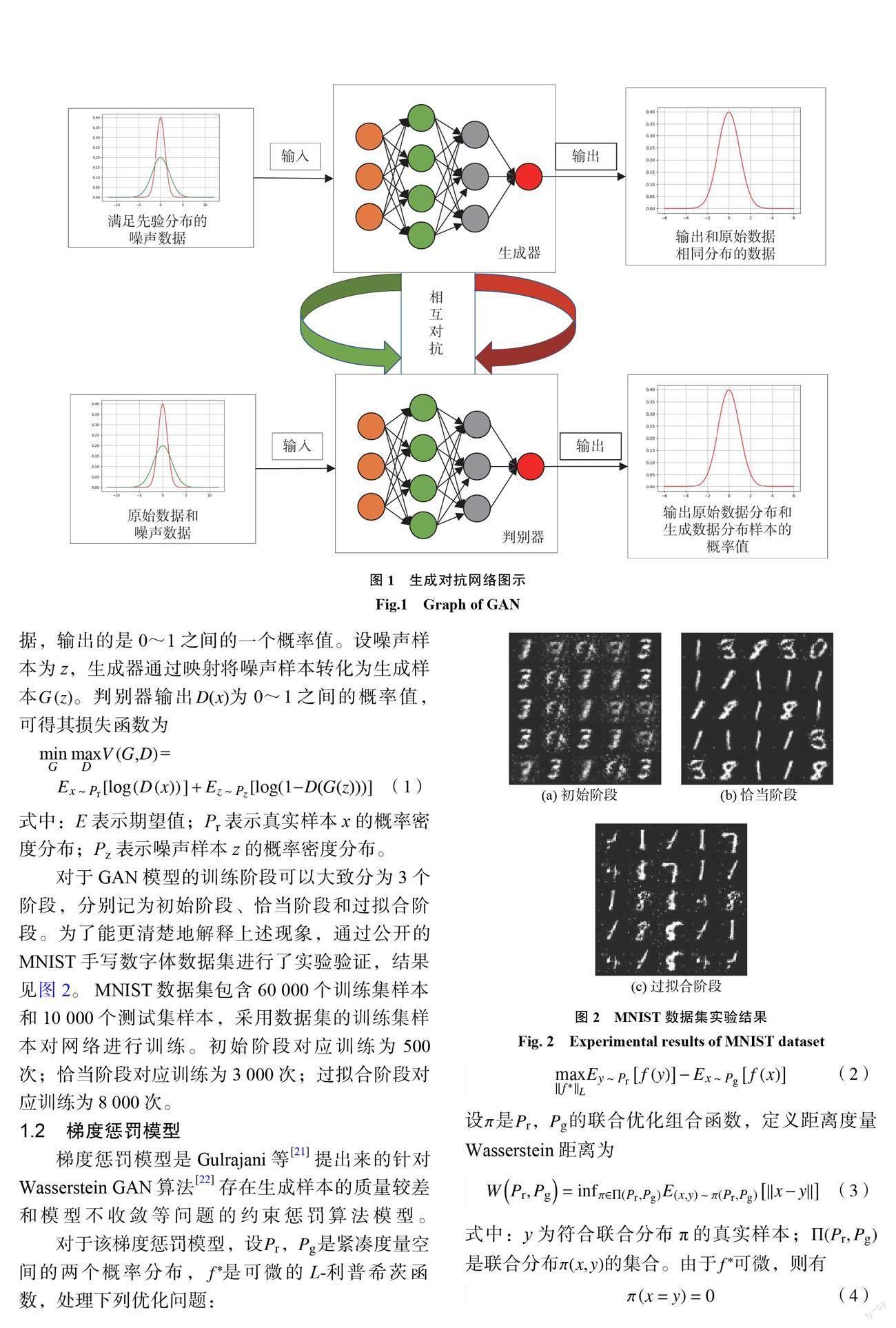
GAN 是 Goodfellow 等提出来的一种神经网络模型，也是一种无监督的生成模型。它由生成器网络和判别器网络两部分组成，网络模型结构如图1所示。 GAN 也是一个相互博弈的对抗模型，是判别器和生成器之间的相互博弈。其中，生成器是通过对先验噪声的学习，学习原始数据的概率密度分布；判别器主要对输入数据进行判断，判断数据是原始数据或者是生成器网络生成的数据，输出的是0～1之间的一个概率值。设噪声样本为 z ，生成器通过映射将噪声样本转化为生成样本G（z）。判别器输出 D（x）为0～1之间的概率值，可得其损失函数为

式中：E 表示期望值；Pr 表示真实样本 x 的概率密度分布； Pz 表示噪声样本 z 的概率密度分布。

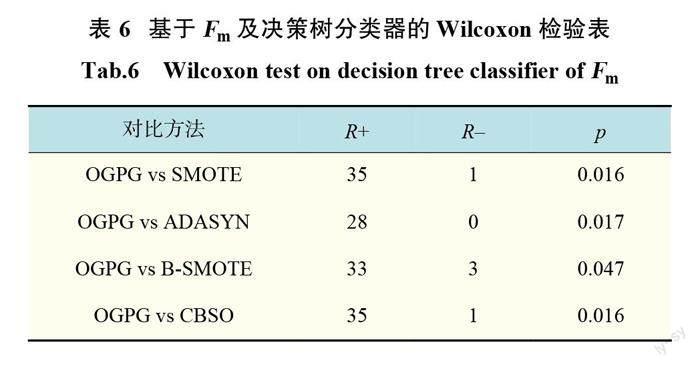
对于 GAN 模型的训练阶段可以大致分为3个阶段，分别记为初始阶段、恰当阶段和过拟合阶段。为了能更清楚地解释上述现象，通过公开的 MNIST 手写数字体数据集进行了实验验证，结果见图2。 MNIST 数据集包含60000个训练集样本和10000个测试集样本，采用数据集的训练集样本对网络进行训练。初始阶段对应训练为500次；恰当阶段对应训练为3000次；过拟合阶段对应训练为8000次。

1.2 梯度惩罚模型

梯度惩罚模型是 Gulrajani 等[21]提出来的针对 Wasserstein GAN 算法[22]存在生成样本的质量较差和模型不收敛等问题的约束惩罚算法模型。

对于该梯度惩罚模型，设Pr ，Pg 是紧凑度量空间的两个概率分布， f *是可微的 L-利普希茨函数，处理下列优化问题：

设π是Pr ，Pg 的联合优化组合函数，定义距离度量 Wasserstein 距离为

式中：y 为符合联合分布π的真实样本；Ⅱ（Pr ; Pg ）是联合分布π（x;y）的集合。由于f *可微，则有

即，对于所有的 L-利普希茨函数几乎都满足，若该函数可微则处处都有梯度，且梯度的范数值为1。根据上述理论知识， Ishaan 等研究者将梯度范数约束在不大于1的范围之内，提出如下新的约束惩罚：

式中： LGP表示梯度惩罚损失；?（x）表示训练样本；ⅡΔ?（x）Dw（?（x））Ⅱ2表示 Wasserstein GAN 中判别器网络输入项梯度的二范数；α是梯度惩罚因子； w 是判别器网络的参数，即D（?（x）; w）。

2 基于梯度惩罚生成对抗网络的过采样算法

由于传统的过采样算法没有充分考虑原始样本的概率密度分布，且易导致生成低质量的样本，因此本文引入生成对抗网络模型和梯度惩罚模型，提出了一种基于梯度惩罚生成对抗网络的过采样算法（OGPG）来解决上述问题。

在 OGPG 算法中，为防止少数类样本过少导致网络模型学习不到原始数据的有效信息，先对原始数据中的少类样本自适应生成部分样本。该算法主要包括3个步骤。

a.去除噪声样本。

在数据预处理阶段，先处理原始数据中存在的噪声数据。对每个样本采用 k 近邻算法，计算样本点与其他样本点的距离，找到该样本点的 k 个最近邻样本点，如果该样本点的标签与 k 近邻中的所有样本点的标签不一致，则认定为噪声数据，并删除该样本点。

b.合成部分少数类样本。

在步骤（a）的基础上，通过线性插值优先合成部分少数类样本数据，通过合成后的样本，学习样本的均值和方差，以便后续训练网络生成新的样本。

首先，设 T 为去噪后原始数据的总样本集合， Tmaj为多数类样本集合， Tmin为少数类样本集合，则有

过采样所需要的生成的样本量

接着，采用线性插值合成部分少数类样本，对于任意的Tmin中的一个样本点xi，运用欧氏距离度量，随机选取 k 近邻中的一个近邻样本xj，通过线性插值合成样本?（x），

式中，? e [0;1]，通过线性插值合成的样本量集合记为T syn。通过合成少数类样本后得到新的少数类样本集合记为Tnew_min 。其中，

c.生成新样本。

结合生成对抗网络模型和梯度惩罚模型优良性质，针对过采样问题提出了改进后的损失函数为

式中， P?（x）表示真实数据分布和生成数据分布采样的线性均匀采样分布，即?（x）=βxr+（1一β）xg ;β e （0;1）。

通过步骤（a）的去除噪声和步骤（b）合成部分少数类样本之后，采用梯度惩罚生成对抗网络算法生成新样本。

首先，把合成的新的少数类样本记为新少数类样本，即Tnew_min 。通过计算得到该样本的均值和方差，分别记为?和σ2。对于噪声样本 z ，假设满足

噪声数据通过映射将数据转化为生成样本

接着，将噪声样本和新少数类样本分别用生成器网络和判别器网络进行迭代，计算各个网络及梯度惩罚的损失，由式（12）得到判别器损失 LD 、生成器损失 LG 和梯度惩罚损失 LGP ，分別为

式中： x为训练样本；∥ΔxD（x）∥2为求该样本的梯度的二范数。

再设置判别器网络和生成器网络的收敛阈值，在达到阈值之后停止迭代，实验设置循环迭代阈值为3000次。最后，通过网络收敛时生成器生成的样本即为新样本，通过梯度惩罚的生成对抗网络模型生成的样本集合记为Tgen。

根据上述对于 OGPG 算法步骤的描述，给出算法的合成样本示意图，见图3。

3 实验结果及分析

3.1 数据集

为了验证 OGPG 算法的有效性，实验从 UCI 机器学习库中挑选了14组二类不平衡数据集，其样本量、特征数以及不平衡率（imbalanced ratio ，IR）都不相同。表1是所选取的数据集的详细信息：

3.2 评价指标

在处理不平衡数据的分类问题的时候，分类器的超平面会向少数类样本偏移，因此精确率不适合作为评价指标。实验采用 Fm 和 Gm 作为评价指标[23]。其中 Fm 表示单一类别精确率和召回率的均衡指标， Gm 表示召回两个类别数据的综合表现指标。Fm 和 Gm 的计算式如下：

式中： TP 表示将正例样本预测为正例；FP 表示将正例样本预测为反例；FN 表示将反例样本预测为正例； TN表示将反例样本预测为反例； P 为查准率； R 为召回率； S 为特异性。

3.3 实验分析

为了验证 OGPG 算法的优越性，首先通过前8组数据集对比了 SMOTE， ADASYN ，B-SMOTE， CBSO[24]传统过采样算法。其次通过后4组数据集对比了采用 GAN 的 LGOS 算法。此外，在对比传统算法中，采用 k 近邻分类器和决策树分类器随机选取70%的数据作为测试集，剩余30%的数据作为测试集，每个数据集取5次实验结果的平均值作为报告结果。在对比 LGOS 算法中采用决策树分类器选取80%的数据作为测试集，剩余20%的数据作为测试集，每个数据集取10次实验结果的平均值作为报告结果。粗体表示的是实验的最优值。通过上述实验验证本算法的有效性和泛化能力。所有实验都是在2.80 GHz CPU 、16.0 GB 内存的电脑上运行的，软件环境是 Python3.7。

从表2和表3的结果可以看出，无论是 k 近邻分类器还是决策树分类器， OGPG 算法在 Fm， Gm 上均获得了明显提升。在 Fm 指标下，8个数据集中都表现较好；在 Gm 指标下，8个数据集中7个表现相对较好。通过对表2、表3对各指标的分析，可以发现算法在 Gm 指标下 abalone3vs11数据集上表现相对没有优势。该数据集在 CBSO 算法上表现相对较好，之所以出现该现象，是因为数据集中存在边界较难学习的样本， OGPG 算法较难学习到该样本的有效信息，导致评价指标相对较低。但是从结果上看仍然非常接近最优指标，充分说明了 OGPG 算法的有效性。通过上述对表2和表3的结果分析，验证了 OGPG 算法的有效性。

为了验证 OGPG 算法的稳定性，实验绘制了数据集在 Fm 指标和 Gm 指标下的箱线图，分别见图4和图5。箱线图包括一个矩形箱体和上下两条线，箱体中间的线为中位线，上限和下限分别为上四分位数和下四分位数，箱子的宽度显示数据的波动程度，箱体的上下方各有一条线是数据的最大值和最小值，超出最大最小值线的数据为异常数据。从图4和图5中可以看出， OGPG算法的数据波动性相对较小，数据的中值、上下四分位数与其他算法相比要更加稳定，且数值也优于其他算法，这说明了 OGPG 算法稳定性较好。

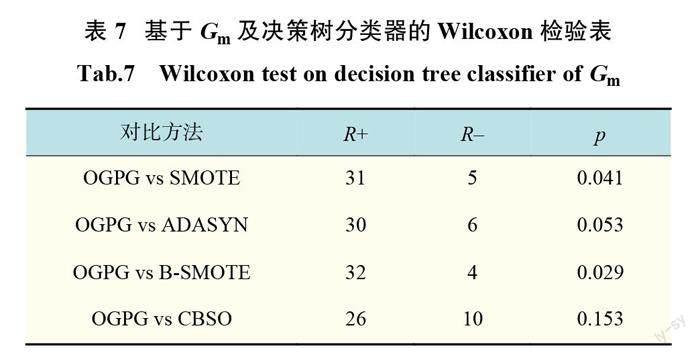
为了验证 OGPG 算法在统计学上是否具有显著性，本文采用 Wilcoxon符号秩检验来评估所提算法和其他对比算法之间的显著性差异。表4～表7是 Wilcoxon符号秩检验的结果，其中 R+表示所提算法的秩和， R–表示对比算法的秩和，置信度是95%，p 为0.05。在 k 近邻分类器下，可以看到，都是拒绝原假设；在决策树分类器下，在对比算法 ADASYN 、CBSO 在 Gm 指标下是接受原假设，其余都是拒绝原假设，说明 OGPG 算法相对于其他算法具有较显著的差异性。结合表2、表3在各指标的综合表现情况，说明 OGPG 算法相对于传统算法有显著的有效性。

为了全面验证算法的有效性，实验还对比了文献[18]的 LGOS 算法，即采用 GAN 的过采样算法，如表8所示。从表8的结果可以看出，在决策树分类器下，无论是 Fm 还是 Gm 指标，该算法均有较为明显的提升。除此之外，在前8组数据集中，样本量相对较少，在对比传统算法中有显著提升；在后6组数据集中，数据样本量相对较多，在对比算法中同样有着较为明显的提升，说明了算法的有效性。

OGPG 算法和 LGOS 算法之间的显著性差异见表9。可以看出，在置信度为95%的情况下，即 p 不大于0.05的情况下，均拒绝原假设。说明 OGPG 算法相对于 LGOS 算法具有显著的差异性。通过该部分实验也说明了 OGPG 算法具有显著的有效性。

4 结束语

针对不平衡数据分类问题，传统的过采样算法没有充分考虑原始数据的概率密度分布，从而导致生成的样本不具有较强的安全性。通过引入生成对抗网络以及梯度惩罚模型，提出了一种基于梯度惩罚生成对抗网络的过采样算法。在该算法中，首先引入生成对抗网络，通过生成器网络有效地学习原始数据的概率密度；其次，由于生成对抗网络易出现过拟合或梯度消失等现象，因此采用梯度惩罚来对判别器网络输入项的梯度二范数进行约束，从而有效地降低了该情况的发生，使得生成器既能有效学习数据的概率密度分布又能合理地生成新样本；最后，在14个公共数据集上采用两个分类器与多种算法进行了对比实验，并利用 Wilcoxon符号秩检验验证了所提算法的有效性和通用性。当然，该算法也有一定的缺点，在时间复杂度上，因为算法引入了深度学习网络，所以时间复杂度上较高，这也是后续将要努力的方向。

参考文献：

[1] FIORE U， DE SANTIS A， PERLA F， et al. Using generative  adversarial  networks  for  improving classification effectiveness in credit card fraud detection[J]. Information Sciences， 2019， 479：448–455.

[2] FOTOUHI S， ASADI S， KATTAN M W. A comprehensive data level analysis for cancer diagnosis on imbalanced data[J]. Journal of Biomedical Informatics， 2019， 90：103089.

[3] MENA L J， GONZALEZ J A. Machine learning for imbalanced  datasets：  application  in  medical diagnostic[C]//Proceedings of the Nineteenth International Florida  Artificial  Intelligence  Research  Society Conference. Melbourne Beach： AAAI Press， 2006：574–579.

[4]武文娟， 李勇. Emfacenet：一種轻量级人脸识别的卷积神经网络[J/OL].小型微型计算机系统， 2021：1–6.（2021-12-17）. http：//kns.cnki.net/kcms/detail/21.1106.tp.20211214.1436.004.html.

[5]周建含， 李英梅， 李文昊.一种改进的半监督集成软件缺陷预测方法[J].小型微型计算机系统 ， 2021， 42（10）：2196–2202.

[6] ZHANG H L， LIU G S， PAN L， et al. GEV regression with convex  loss  applied  to  imbalanced  binary classification[C]//2016 IEEE First International Conference on Data Science in Cyberspace （DSC）. Changsha： IEEE， 2016：532–537.

[7] JING X Y， ZHANG X Y， ZHU X K， et al. Multiset feature learning for highly imbalanced data classification[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence， 2021， 43（1）：139–156.

[8] ZHENG Z Y， CAI Y P， LI Y. Oversampling method for imbalanced classification[J]. Computing and Informatics， 2015， 34（5）：1017–1037.

[9] CASTRO C L， BRAGA A P. Novel cost-sensitive approach to improve the multilayer perceptron performance on imbalanced data[J]. IEEE Transactions on Neural Networks and Learning Systems， 2013， 24（6）：888–899.

[10] WANG C， DENG C Y， YU Z L， et al. Adaptive ensemble of classifiers with regularization for imbalanced dataclassification[J]. Information Fusion， 2021， 69：81–102.

[11]周传华， 朱俊杰， 徐文倩， 等.基于聚类欠采样的集成分类算法[J].计算机与现代化， 2021（11）：72–76.

[12]陳刚， 郭晓梅.基于时间序列模型的非平衡数据的过采样算法[J].信息与控制， 2021， 50（5）：522–530.

[13] CHAWLA N V， BOWYER K W， HALL L O， et al. SMOTE： synthetic minority over-sampling technique[J]. Journal of Artificial Intelligence Research， 2002， 16：321–357.

[14] HE H B， BAI Y， GARCIA E A， et al. ADASYN： Adaptive synthetic  sampling  approach  for  imbalanced learning[C]//2008 IEEE International Joint Conference on Neural Networks （IEEE World Congress on Computational Intelligence）. HongKong， China： IEEE， 2008：1322–1328.

[15] HAN H， WANG W Y， MAO B H. Borderline-SMOTE： a new over-sampling method in imbalanced data sets learning[C]//International  Conference  on  Intelligent Computing. Berlin， Heidelberg： Springer， 2005：878–887.

[16] GOODFELLOW I J， POUGET-ABADIE J， MIRZA M， et al. Generative adversarial nets[C]//Proceedings of the 27th International Conference on Neural Information Processing Systems. Montreal： MIT Press， 2014：2672–2680.

[17] DOUZAS G，  BACAO F. Geometric  SMOTE a geometrically  enhanced  drop-in  replacement  for SMOTE[J]. Information Sciences， 2019， 501：118–135.

[18]何新林， 戚宗锋， 李建勋.基于隐变量后验生成对抗网络的不平衡学习[J].上海交通大学学报 ， 2021， 55（5）：557–565.

[19] LUO X， CHANG X H， BAN X J. Regression and classification using extreme learning machine based on L1- norm and L2-norm[J]. Neurocomputing， 2016， 174：179–186.

[20] CUZICK J. A Wilcoxon ‐ type test for trend[J]. Statistics in Medicine， 1985， 4（1）：87–90.

[21] GULRAJANI I， AHMED F， ARJOVSKY M， et al.Improved training of Wasserstein GANs[C]//Proceedings of the 31st International Conference on Neural Information Processing Systems. Long Beach： Curran Associates Inc. ， 2017：5769–5779.

[22] ADLER  J，  LUNZ  S.  Banach  Wasserstein GAN[C]//Proceedings of the 32nd International Conference on Neural Information Processing Systems. Montréal：Curran Associates Inc. ， 2018：6755–6764.

[23] HE H B， GARCIA E A. Learning from imbalanced data[J]. IEEE Transactions on Knowledge and Data Engineering， 2009， 21（9）：1263–1284.

[24] YU Y， GAO S C， CHENG S， et al. CBSO： a memetic brain storm optimization with chaotic local search[J]. Memetic Computing， 2018， 10（4）：353–367.

（编辑：董 伟）