超高性能混凝土材料-窄幅钢箱组合梁极限承载力计算方法*

黄 荆 莫时旭,2 柴龙杰 郑 艳,2

(1.桂林理工大学土木与建筑工程学院, 广西桂林 541004; 2.广西建筑新能源与节能重点实验室, 广西桂林 541004)

钢-混凝土组合梁由于自重轻、承载力高、刚度大、稳定性好以及施工方便等优点,现已广泛应用于桥梁结构和建筑结构领域[1-2]。但在组合梁的使用过程中,由于混凝土材料的抗拉强度较低,受车辆荷载以及梁自重的影响,负弯矩区的拉应力会导致桥面板受拉区开裂,严重影响了结构的使用寿命。针对桥面负弯矩区开裂问题,目前的解决方法主要有施加预应力法、支点升降法等,此外,聂建国等提出可以在钢梁与混凝土的连接部位采用抗拔不抗剪的连接件,使得钢-混凝土界面在不发生分离的条件下产生自由滑动,从而释放混凝土板的拉应力,降低混凝土板的开裂风险[3]。上述解决方法多为施工过程中对翼板的加强,存在一定的局限性。同时,传统的钢箱组合桥梁,在受力过程中,其下部钢箱产生了部分屈曲变形,如何提高负弯矩区的抗裂能力以及减小钢箱的屈曲成为组合梁结构设计的关键。

超高性能混凝土(UHPC)是一种新型的高性能纤维增强胶结复合材料,基于最大密实度堆积理论配置,通过掺入一定体积的钢纤维,增加了其抗拉性能,使得UHPC材料与传统的混凝土材料相比,具有更高的抗拉强度、抗压强度、耐久性、抗剥落性以及能量吸收能力[4-5]。因此,将UHPC材料替代普通混凝土材料应用于桥梁结构中,可以显著地提高桥梁的抗裂性能,减少结构自重,增加结构的耐久性。

将UHPC材料应用于钢-混凝土组合梁中,提高结构承载力的同时改善负弯矩区的开裂问题成为研究的热点。朱劲松等对4根钢-UHPC华夫板组合梁进行了负弯矩区静力加载试验[6],并基于简化塑性理论,提出了负弯矩区钢-UHPC华夫板组合梁的极限抗弯承载力计算方法。试验结果表明,配筋率的增加可提高构件的承载力和刚度,板肋高厚比的减小会加剧板的裂缝开展,降低试件开裂荷载和初始刚度。王皓磊等对1根钢-UHPC连续组合梁和1根预应力钢-普通混凝土连续组合梁进行静力加载试验[7],对比发现,钢-UHPC梁的名义开裂强度以及极限承载力均大于预应力钢-普通混凝土组合梁,并根据塑性理论得到了钢-UHPC连续组合梁的抗弯承载力计算方法。刘新华等对钢-UHPC组合梁抗裂性能进行研究[8],并通过ABAQUS建立了有限元模型对试验梁进行模拟分析,研究结果表明组合梁负弯矩区采用UHPC可明显提高负弯矩区的开裂性能,且裂缝间距较小,可以明显抑制混凝土裂缝的发展,并提出了相应的UHPC裂缝宽度计算式。罗兵等采用薄层UHPC代替普通混凝土材料,研究了钢-UHPC-NC组合梁的负弯矩受力性能[9],研究结果表明,UHPC层裂缝分布呈现出数量多、宽度小、长度短的特征,其刚度相比于钢-普通混凝土组合梁试件提升了7%,且开裂荷载得到了显著的提升。

Liu等对5个试样进行了四点加载试验,建立了一种高应变硬化超高性能混凝土UHPC梁的极限承载力计算方法[10],研究结果表明:配筋率的增加可以提高极限承载力但当配筋比增加到一定水平时,极限承载力的增长速率减缓。

以上研究多集中于解决负弯矩区的开裂问题,对于组合梁的腹板屈曲方面涉猎较少,且其梁的结构形式多为工字形截面梁,箱型梁作为一种常见的组合梁形式,对其研究较少。针对组合梁负弯矩区开裂以及腹板屈曲问题提出了一种新的结构形式,即UHPC-窄幅钢箱组合梁,通过在组合梁翼板中采用UHPC部分替代普通混凝土材料,来改善梁的负弯矩区开裂状况,在钢箱中部分充填混凝土,抑制钢箱腹板的屈曲,从而提高组合结构整体承载能力。通过分析该种梁型不同配筋率下的受力特征,建立了理论分析模型,提出了钢-UHPC部分填充式窄幅钢箱组合梁的弹性弯矩以及承载力计算方法,成果可为该新型组合梁的设计与应用提供参考。

1 试验概况

1.1 试件设计

共设计制作了3根窄幅钢箱组合梁试件,其基本信息如表1所示,其中A0为NC-窄幅钢箱组合梁试件,SUCB-1、SUCB-2为翼板中UHPC层厚度为50 mm的UHPC-窄幅钢箱组合梁试件。

表1 组合梁基本参数Table 1 Basic parameters of composite beams

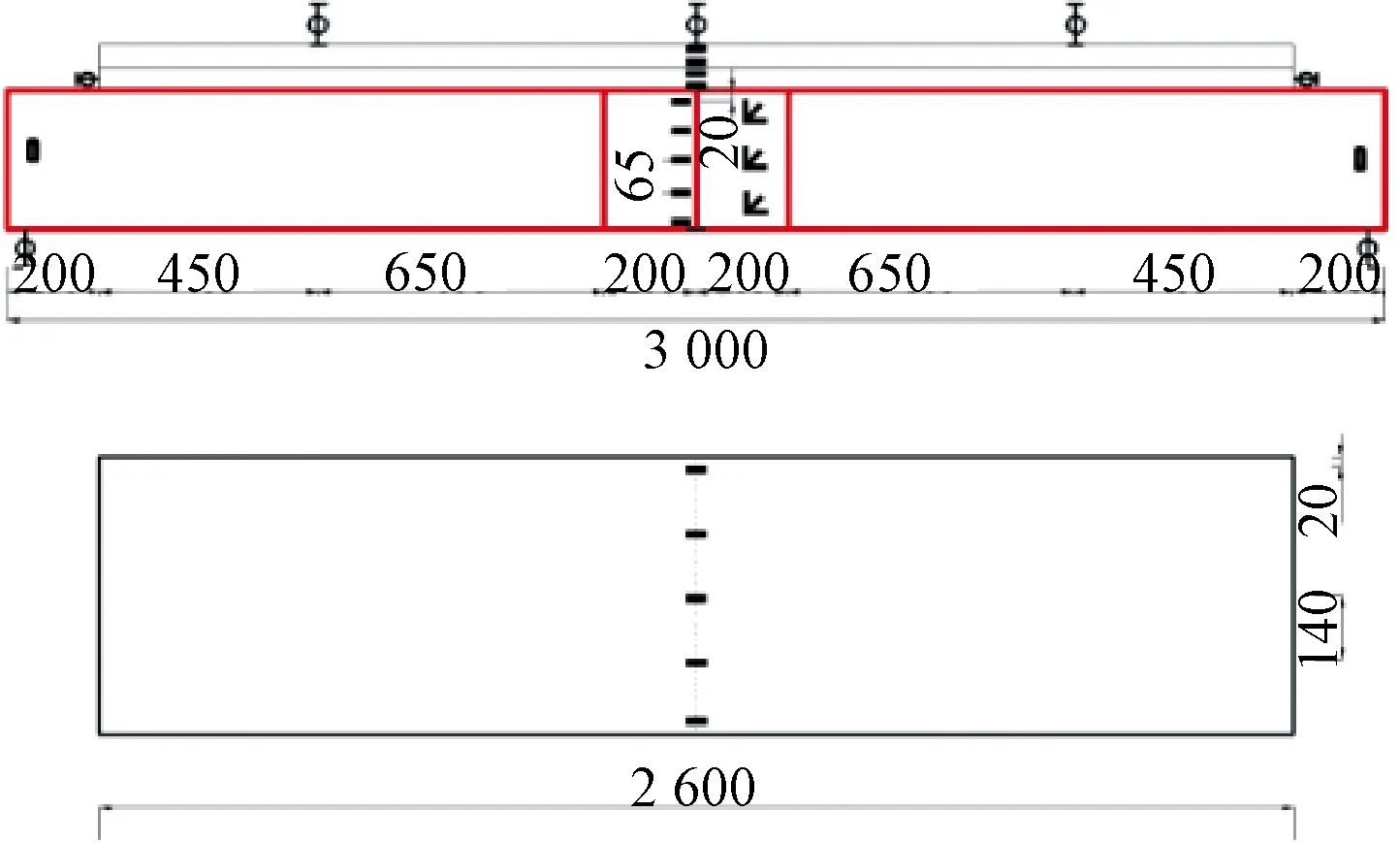
试件跨度3 000 mm,总高度为400 mm,其中钢箱高度为300 mm,腹板翼板高度100 mm,A0翼板均采用C40普通混凝土,其余试件翼板中UHPC层高度以及C40混凝土层高度均为50 mm,为减小下部钢箱的屈曲,所有试件钢箱内均填充无钢纤维掺量的UHPC材料,填充高度为钢箱高度的1/2。纵筋采用直径为14 mm 的Q400级钢筋,长度为2 560 mm,间距为180 mm;箍筋采用Q300级钢材,直径为6 mm,箍筋间距为135 mm。钢箱采用Q235钢板焊接加工而成,钢箱顶板和底板的厚度分别为20 mm和10 mm,隔板的厚度为6 mm,腹板、肋板和端板的厚度均为10 mm。钢箱与混凝土翼板采用栓钉连接,栓钉的设计根据极限平衡法,采用塑性方法设计,栓钉采用两列并排布置,两列间隔160 mm。试件的纵向布置及典型截面如图1、图2所示。

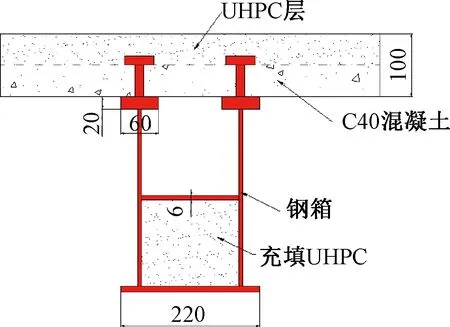
图1 组合梁截面 mmFig.1 Section diagram of the composite beam

图2 试件立面 mmFig.2 Elevation of the specimen

1.2 材料性能

所采用的UHPC配合比如表2所示。

表2 UHPC配合比Table 2 UHPC mix ratios

为测试材料性能,在每个钢箱浇筑的同时,浇筑UHPC试块和C40混凝土试块,其材料试验结果如表3所示。

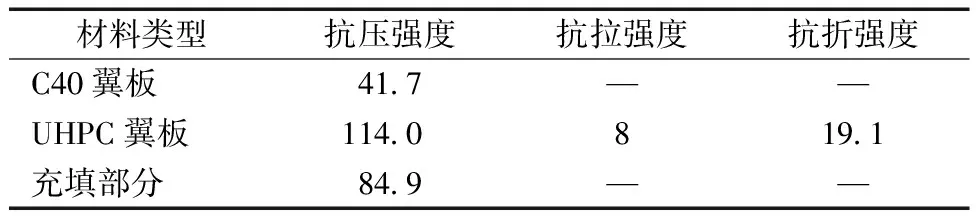
表3 材料性能Table 3 Material properties MPa

试验中钢纤维的直径为0.18～0.22 mm,其长度为13 mm,相关的力学参数如表4所示。

表4 钢纤维的力学参数Table 4 Mechanical parameters of steel fiber

D为钢纤维的直径;L为钢纤维的长度;ft为钢纤维的抗拉强度;Ef为钢纤维的弹性模量

1.3 加载方式

试验采用三点加载的方式。两端支座固定,跨中部位采用千斤顶进行加载,如图3所示。其应变片布置如图4所示。采用位移控制加载,在弹性阶段,以1 mm为一级控制加载,当其达到塑性阶段,将每级加载位移增大到2 mm,每级加载前停留5～10 min,用强光手电以及裂缝观测仪进行裂缝观测和记录。

图3 加载装置Fig.3 Loading device

位移计; 倾角仪; 应变片; 应变花。图4 应变片布置 mmFig.4 Strain gauge arrangement

2 试验结果及分析

2.1 试验现象

3根梁的破坏均为弯曲破坏,其破坏模式如图5所示,各试件破坏均为翼板由于受到负弯矩的作用,使得裂缝贯通,翼板中纵向钢筋拉断或屈服,钢箱下翼缘由于受压而产生局部屈曲变形,其中支座处以及钢箱跨中部分屈曲变形较为明显,钢梁跨中梁肋产生扭转变形,SUCB-1试件中,钢梁腹板部分可见较为明显的向外屈曲变形,因此,部分充填混凝土对钢箱的约束仅限于对于钢箱的内凹变形,而对其外凸变形的约束效果较差。

a—A0破坏特征; b—SUCB-1破坏特征; c—SUCB-2破坏特征。图5 试件主要破坏模式Fig.5 Main failure modes of specimens

各试件的破坏过程相似,在负弯矩作用下,组合梁的跨中位置先出现裂缝,且裂缝一出现即贯通板面,后随着荷载的不断增加,裂缝宽度逐渐增大,裂缝逐渐贯穿翼板,形成几条主裂缝。同时,A0和SUCB-1试件在荷载为251 kN以及747 kN时翼板侧面翼板交界处形成滑移裂缝,由此可知,UHPC与NC材料具有良好的黏结性能,滑移裂缝出现较晚,仅在0.93fu(fu为组合梁极限荷载)处产生第一条滑移裂缝,而普通混凝土之间的黏结性能较差,当荷载达到0.32fu时即出现第一条滑移裂缝。对比试件的裂缝分布可知,普通混凝土翼板A0中出现大量斜向裂缝,且斜向裂缝关于板纵向中线对称布置,原因是普通混凝土板的抗滑移能力较差,栓钉的约束作用显著。

此外,在试验过程中发现,试验梁翼板下部由于栓钉的约束使得出现的裂缝多为斜向裂缝,如图6所示,且在梁的两侧呈对称分布。

图6 翼板底面裂缝分布Fig.6 Cracks distributions on the bottom surface of wing plates

试验梁的端部均产生一定的滑移裂缝,其中A0试件的滑移裂缝最为显著,如图7所示,因此,UHPC与普通混凝土间的黏结强度要远大于普通混凝土间的黏结强度。

a—A0; b—SUCB-1; c—SUCB-2。图7 试验梁端部裂缝分布Fig.7 Crack distributions at the end of the test beam

2.2 荷载挠度曲线

试验梁的荷载-挠度曲线如图8所示,由图可知,试验梁的荷载-挠度曲线大致可以分为四个阶段:第一阶段为开始加载到翼板上部UHPC层开裂,为弹性阶段,荷载-挠度曲线呈线性分布;从开裂到组合梁开始屈服为第二阶段,此阶段被称为裂后弹性阶段,其荷载-挠度曲线仍为线性,但其刚度小于第一阶段,在此阶段中,钢纤维开始发挥桥接作用,钢筋应力也有明显的增强;第三阶段为屈服阶段,在此阶段,组合梁的刚度随着裂缝的开展呈现出非线性特征,裂缝数量增多,主裂缝宽度明显发展;从屈服到破坏为第四阶段,在此阶段,钢筋全部屈服,部分钢筋被拉断,钢箱底部屈曲,为塑性阶段。相关参数如表5所示。

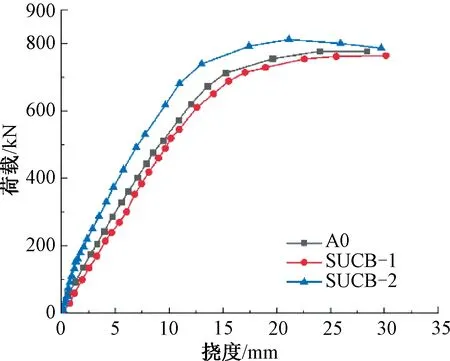
图8 荷载-挠度曲线Fig.8 Load-deflection curves

表5 相关参数Table 5 Related parameters kN

由表5可知,相同配筋率下,相比于普通混凝土翼板,采用UHPC翼板其开裂荷载、屈服荷载以及极限荷载分别提高了74.6%、11.3%、1.5%,裂前刚度提高了8.7%,裂后刚度提高了22%。当配筋率从1%提高到2%时,其开裂荷载、屈服荷载、极限荷载提升相对较小,分别为11.8%、2.2%、3.3%,裂前刚度提高了1倍,裂后刚度提高33.7%。因此,配筋率对于组合梁的刚度影响较为显著。

2.3 荷载-钢筋应力曲线

图9为钢筋屈服前的荷载-应力曲线,由图可知,当荷载小于开裂荷载时,其荷载-应力曲线近似为线性关系,钢筋的应力在翼板出现第一条裂缝时存在较大的突变,由于水泥基体的开裂,应力进行重分布,部分应力转移到了钢筋中,使得钢筋应力存在激增的现象。SUCB-1、SUCB-2组合梁翼板中的钢筋具有较高的屈服荷载,钢筋的屈服荷载可达到组合梁试件极限荷载的65%以上。A0组合梁翼板由于没有钢纤维的桥接作用,使得开裂后,水泥基体退出工作,所有的应力均由钢筋承担,故相比于UHPC组合梁翼板,在相对较小的荷载下,钢筋应力即达到屈服强度。

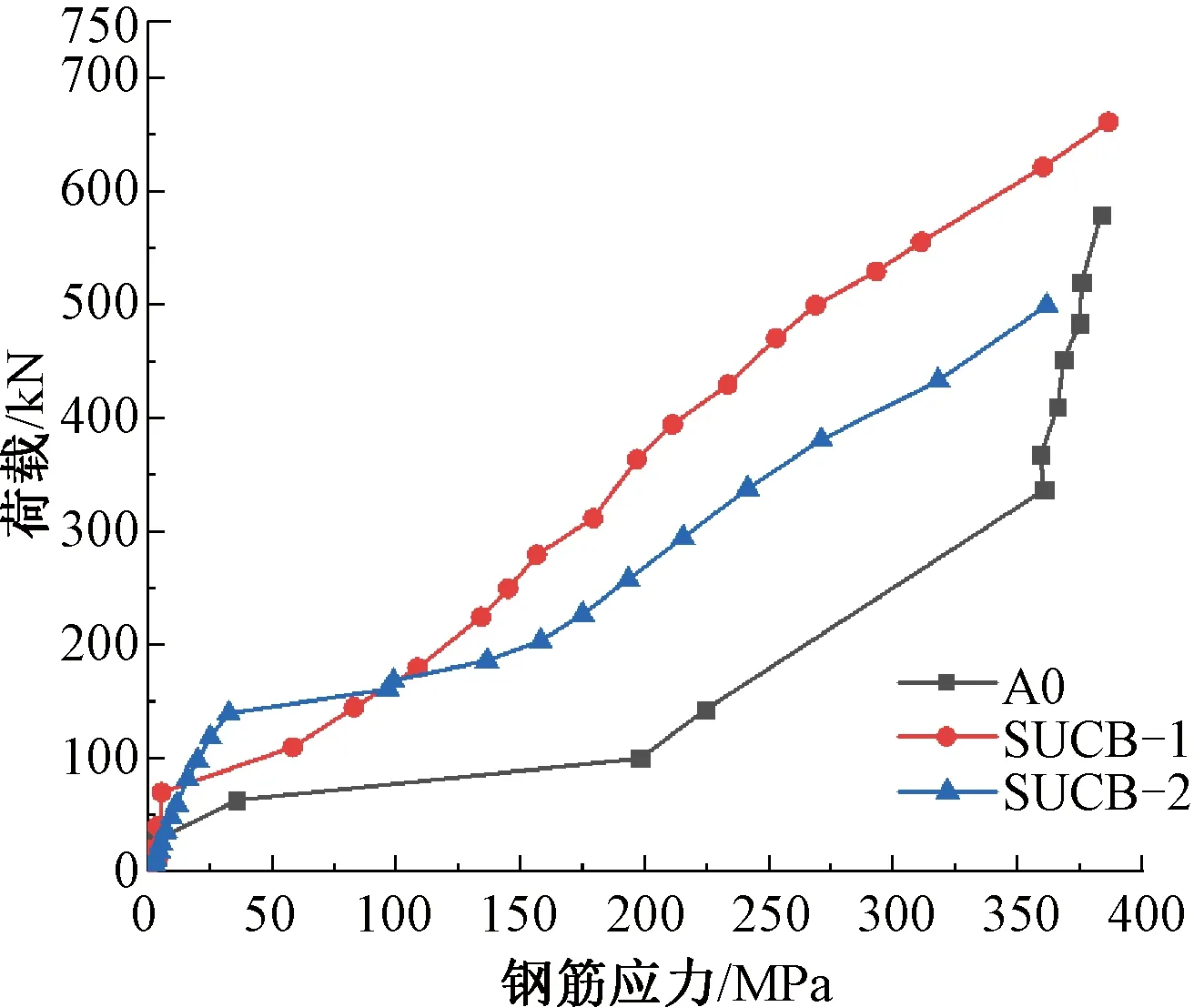
图9 荷载-钢筋应力曲线Fig.9 Load-reinforcement stress curves

2.4 钢箱应变

图10为钢箱下缘的荷载-应变曲线,由图可知,钢箱的应变可以分为三个阶段,即弹性阶段、裂后弹性阶段以及屈服阶段。

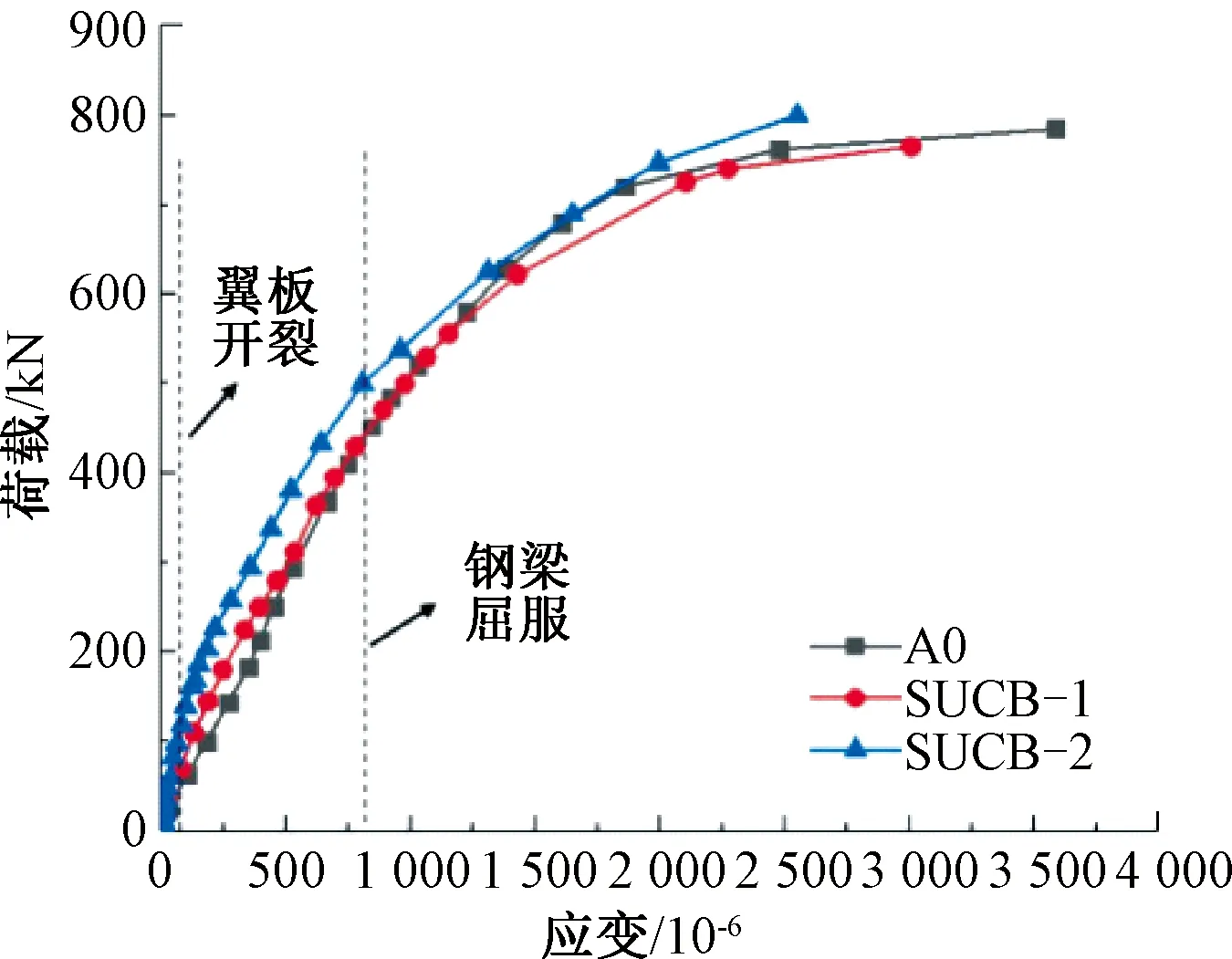
图10 钢箱下缘荷载-应变曲线Fig.10 Load-strain curves at lower edge of steel box

开裂前弹性阶段,试件的变化规律基本相同,开裂后到钢箱屈服阶段,A0以及SUCB-1的应变发展速率明显快于SUCB-2,说明采用UHPC翼板以及采用较高的配筋率均有助于梁裂后刚度的提升。当进入破坏阶段时,应变均达到了2 500×10-6,钢箱的塑性发展较为充分。

2.5 最大裂缝宽度

在负弯矩的作用下,荷载与UHPC翼板顶部最大裂缝宽度曲线如图11所示,由图可知,当裂缝宽度小于0.2 mm时,荷载与最大裂缝宽度关系近似线性;当接近组合梁的屈服荷载后,其最大裂缝宽度增长速率明显提升,且当配筋率为2%时其裂缝宽度增加速率相比于1%的配筋梁有所减小。A0试件的最大裂缝宽度增长速率慢于UHPC梁,原因是,A0试件最终破坏时裂缝宽度分布相对均匀,无明显的主裂缝。而UHPC试件的裂缝比较规整,为几条主裂缝发展,伴有较少的次要裂缝,因此UHPC组合梁翼板的拉应力主要在一条或几条主裂缝处释放,从而导致主裂缝发展迅速,其余裂缝宽度基本不变,而A0试件裂缝发展分布较为杂乱,从而使得拉应力在板面的释放较为均匀,因此,其裂缝多,而最大裂缝发展速度较慢。

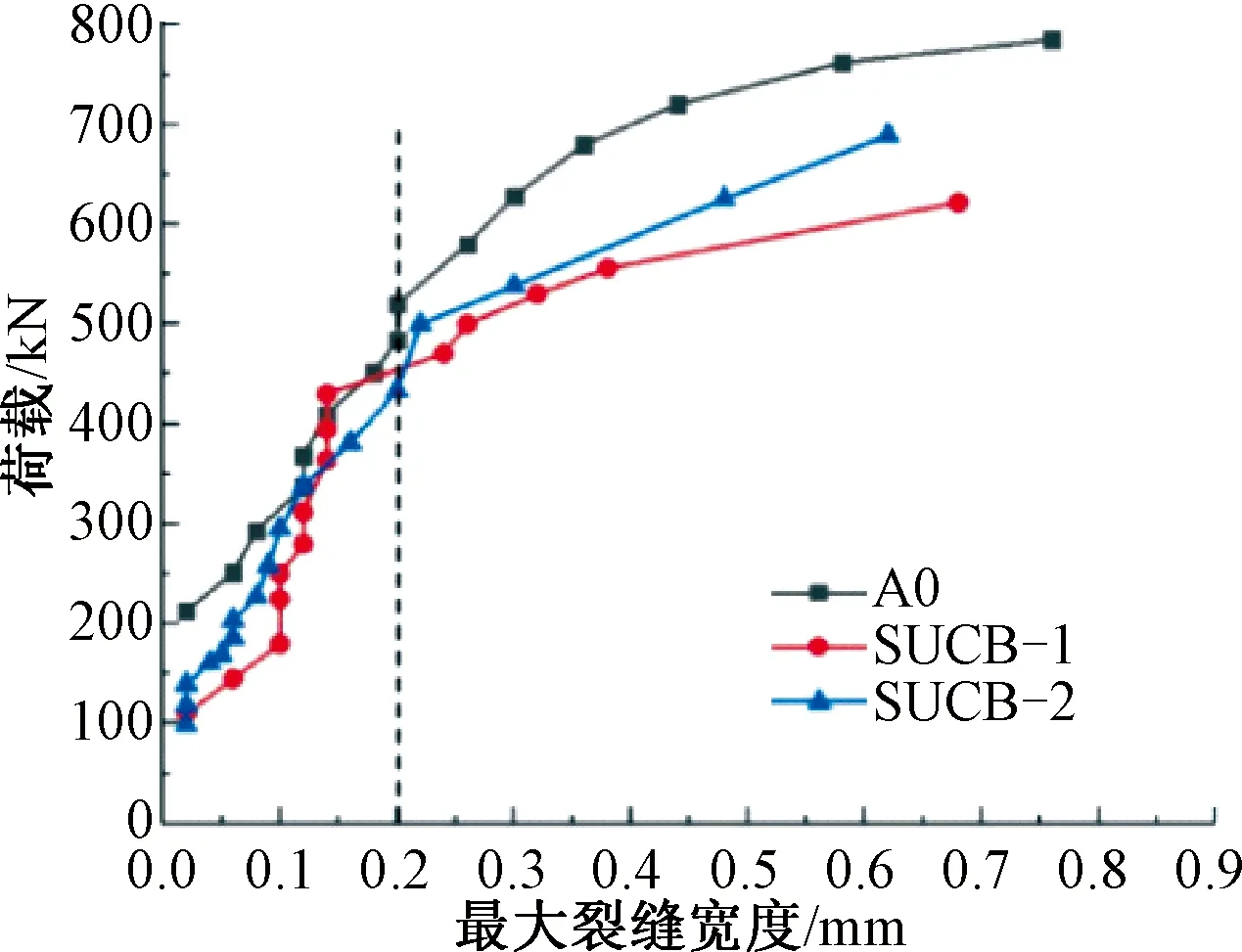
图11 荷载-最大裂缝宽度曲线Fig.11 Curves of load-maximum crack width

2.6 荷载-滑移曲线

在加载过程中可以在翼板的侧面交接位置观察到较为明显的水平滑移裂缝,为进一步对比分析三根梁的滑移情况,实测了三根梁的荷载-滑移曲线,其结果如图12所示,由图可知,普通混凝土翼板组合梁的最大滑移为2.0 mm,配筋率为1%的UHPC翼板组合梁最大滑移为0.7 mm,配筋率为2%的UHPC翼板组合梁的最大滑移为1.25 mm。因此UHPC组合梁的滑移要明显的小于普通混凝土组合梁,这主要是由于UHPC与NC的黏结性能要比普通混凝土之间的黏结性能强很多,这也是A0试件在0.32fu处即出现滑移裂缝的原因。

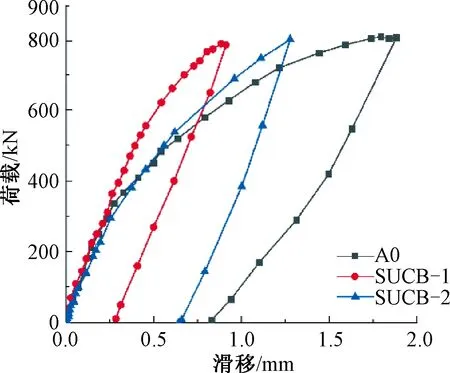
图12 荷载-滑移曲线Fig.12 load-slip curves

2.7 平截面假定验证

UHPC梁正截面承载力的计算以平截面假定为基础,因此需要对梁的平截面假定进行验证,各梁跨中应变沿截面梁高度分布如图13所示,由图可知,其应变沿梁截面高度的分布近似线性,基本符合平截面假定。

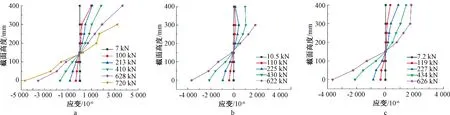
a—A0; b—SUCB-1; c—SUCB-2。图13 应变沿截面梁高的分布Fig.13 Strain distributions along section beam height

3 理论计算

3.1 UHPC抗拉强度

由于UHPC中掺有一定数量的钢纤维,故相比于普通混凝土材料,其开裂后仍具有较强的抗拉强度,在理论分析时,UHPC所提供的抗拉强度值不可忽略,文献[11-12]提出了考虑上述因素影响下的UHPC裂后抗拉强度计算方法,其计算式如下:

(1)

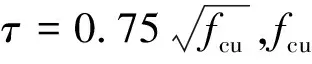
(2)

3.2 基本假设

1)忽略混凝土板与钢梁之间的竖向分离。

2)钢-UHPC界面滑移对承载能力的削弱效应忽略不计。

3)受力全过程中满足平截面假定。

4)不考虑普通混凝土的拉应力。

5)忽略钢箱厚度。

3.3 UHPC本构模型

根据法国规范[14]采用双线性模型来表征UHPC的受压行为。所采用的本构模型如图14所示[11],其抗压本构表达式为:

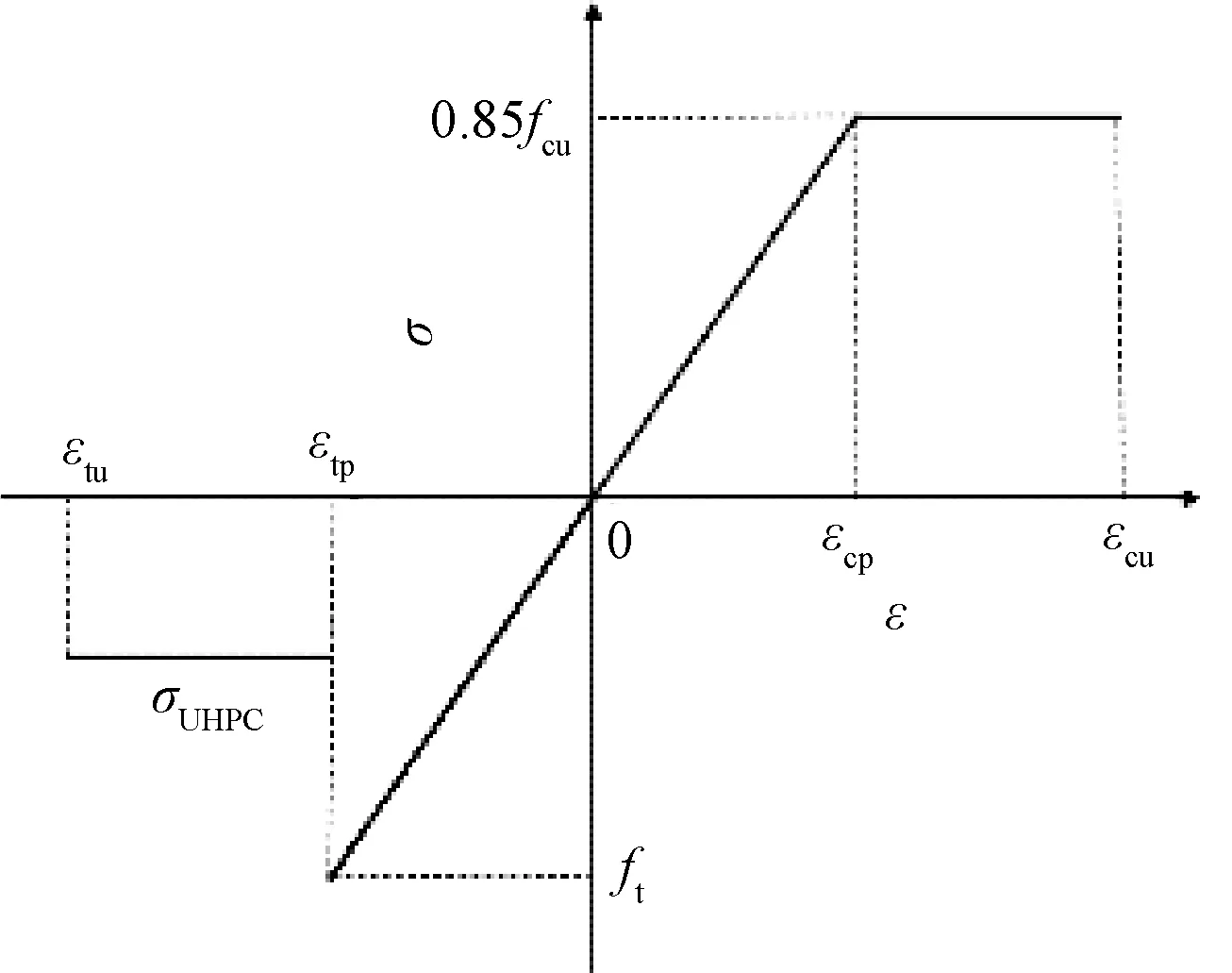
图14 UHPC本构模型Fig.14 UHPC constitutive model

(3)

式中:σc为压应力;εc、εcp和εcu分别为压应变、极限弹性压应变和极限压应变;Ec为UHPC受压时的弹性模量;fcu为UHPC立方体抗压强度。

UHPC拉伸本构关系式为:

(4)

式中:σt为拉应力;εt、εtp和εtu分别为拉应变、极限弹性拉应变和极限拉应变;Et为UHPC受拉时的弹性模量。

3.4 分析模型

3.4.1组合梁弹性阶段分析

将钢-UHPC窄幅钢箱连续组合梁分为弹性阶段和极限阶段两部分进行分析,组合梁开裂前,受拉部分的拉应力主要由UHPC层、钢筋承担,此时,UHPC层处于弹性状态,受压区由钢箱和充填部分无钢纤维掺量的UHPC提供,其应力、应变如图15所示。

由内力以及弯矩平衡可得:

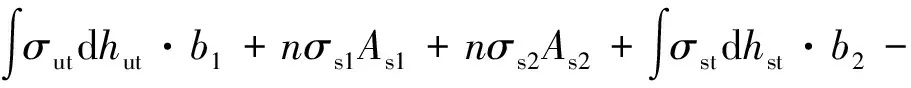
(5a)

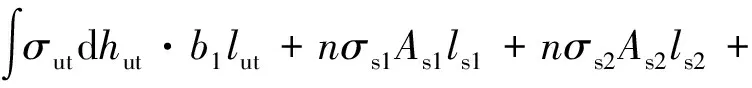
(5b)

式中:σut为UHPC层的应力分布函数;σs1为翼板中上层钢筋的应力;σs2为翼板中下层钢筋的应力;σst、σsc分别为钢箱受拉、受压部分的应力分布函数;σcu为钢箱中部分充填混凝土的受压分布函数;hut、hst、hsc、hcu分别为受拉区UHPC层的厚度、钢箱受拉区的高度、钢箱受压区高度、充填混凝土高度;b1、b2为组合梁翼板宽度和钢箱宽度;lut、ls1、ls2、lst、lsc、lcu分别为UHPC层、上、下层钢筋、钢箱受拉区、钢箱受压区以及充填部分混凝土形心到中性轴的距离。

积分后式(5a)及式(5b)可以表示为式(6a)～(6b):

(6a)

2nσs2As2ls2+σsthstltsb2-σschsclscb2-

(6b)

由几何关系可将各部分应变用最大拉应变值ε1表示,如式(7)所示:

(7a)

(7b)

(7c)

(7d)

(7e)

(7f)

式中:ε2、ε3、ε4分别为UHPC-NC交界面、钢箱顶部以及钢箱底部的应变,ε1根据文献[15]进行取值;εs1、εs2、εcu分别为上层钢筋、下层钢筋和部分充填混凝土顶部的应变;H为组合梁的总高度。

根据材料力学理论,UHPC弹性模量采用文献[16]中所提出的数值。将式(7)代入式(6a),经过迭代计算,得到中性轴高度,后代入式(6b),得到开裂弯矩。将开裂弯矩值与试验值进行对比,结果如表6所示。由表可知,其计算值与实际值吻合较好,但试验值的结果普遍大于理论值,原因是在计算时忽略了普通混凝土的贡献。

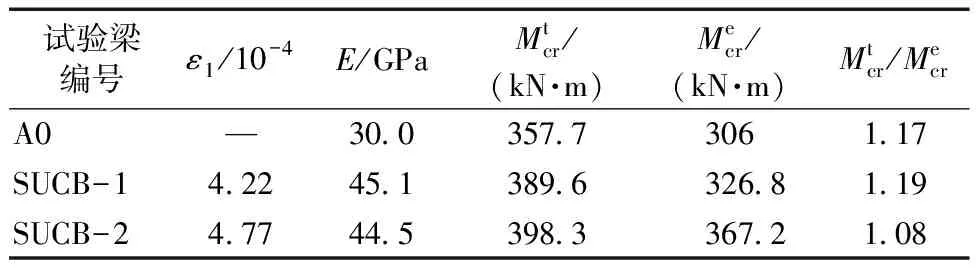
表6 弹性阶段理论值与试验值对比Table 6 Comparisons of theoretical and experimental values in the elastic stage

3.4.2极限承载能力计算

UHPC开裂后,仍然具有一定的抗拉强度,当达到极限承载能力时,根据前面所提出的本构模型,得到UHPC-窄幅钢箱组合梁的计算模型,如图16所示。

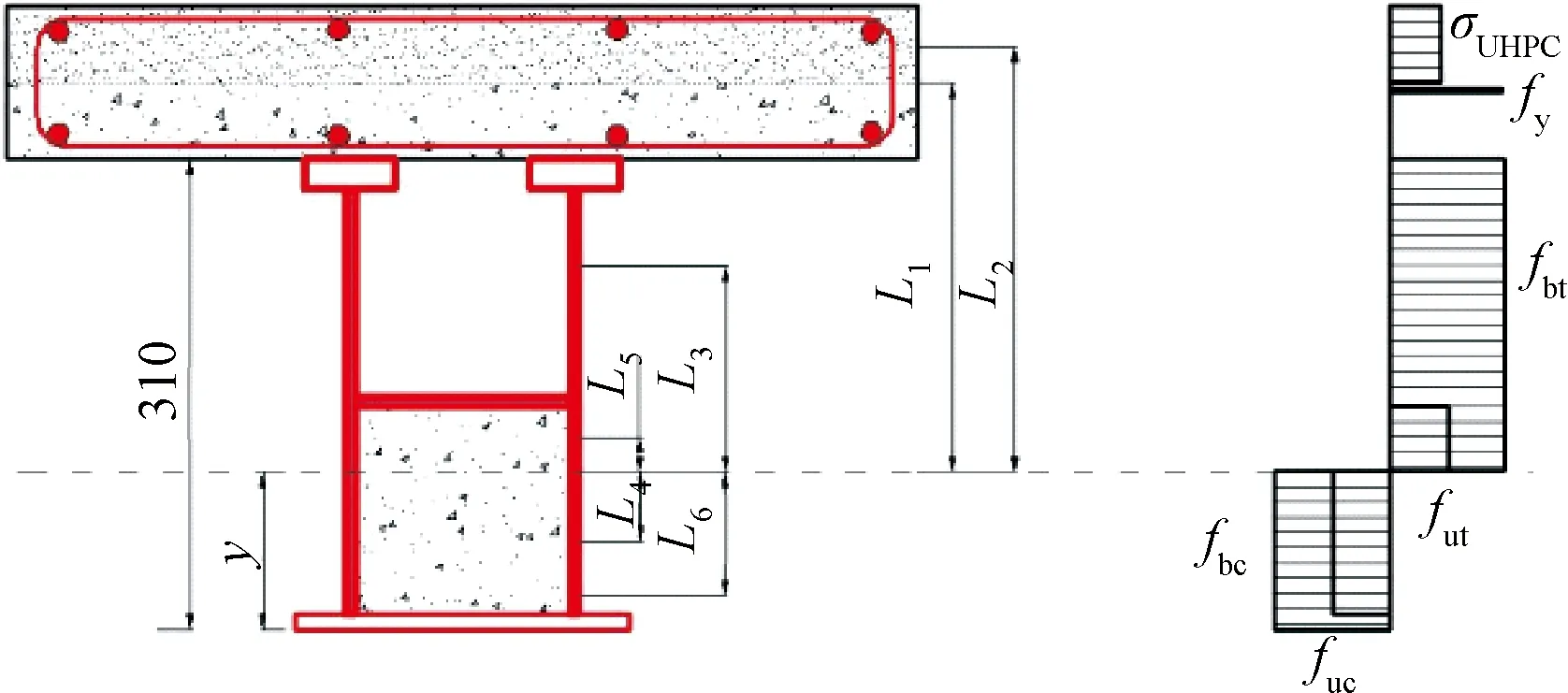
图16 极限状态下组合梁计算模型 mmFig.16 Calculation model of the composite beam in limit state

其中开裂后UHPC的拉应力由式(2)求得,UHPC开裂后拉应力如表7所示。

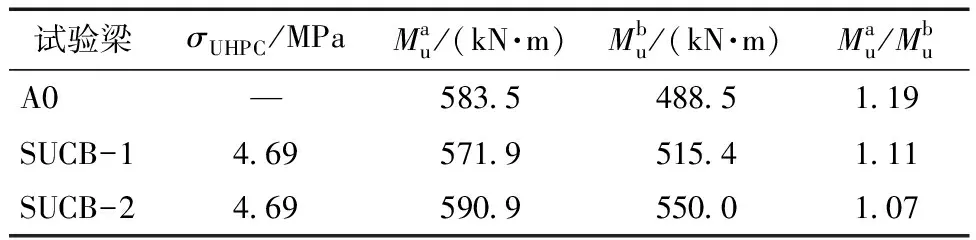
表7 极限弯矩试验值与计算值对比Table 7 Comparisons of test values and calculated values of ultimate bending moment

由内力以及弯矩平衡公式可得,

σUHPCAUHPC+fyAs+fbtAbt+futAut=fucAuc+fbcAbc

(8a)

M=σUHPCAUHPCl2+fyAsl1+fbtAbtl3+

fucAucl4+futAutl5+fbcAbcl6

(8b)

式中:σUHPC为开裂后UHPC的拉应力;fy、fbt、fut、fuc、fbc分别为钢筋的拉应力、钢箱受拉区的应力、充填部分受拉区的应力、充填部分受压区的应力以及钢箱受压区的应力;AUHPC、Abt、Aut、As、Auc、Abc分别为翼板UHPC层、钢箱受拉区、充填部分受拉区、钢筋、充填部分受压区以及钢箱受压区的面积;L1、L2、L3、L4、L5、L6分别为UHPC层、钢筋、钢箱受拉区、充填部分受压区、充填部分受拉区、钢箱受压区合力点到中性轴的距离。

通过式(8a)计算得到组合梁中性轴的高度y,后将y代入式(8b),解得各组合梁的极限弯矩。其计算结果如表7所示。A0试件的实测值与理论值之比为1.19,相差较大,原因是在计算时忽略了混凝土翼板对极限承载能力的贡献,导致其计算结果比实际值偏小。而SUCB-1和SUCB-2试件试验值与计算值吻合度较高。

4 试验梁非线性有限元分析

为了进一步保证试验结果可靠,采用ABAQUS软件对试验梁进行加载的全过程分析,以进一步分析UHPC-窄幅钢箱组合梁的受力性能。

4.1 有限元模型的建立

通过ABAQUS软件进行有限元建模分析。其中,钢梁、充填部分、翼板以及栓钉均采用八结点缩减单元(C3D8R)模拟。钢筋、箍筋采用三维两结点线性杆单元(T3D2)模拟。将钢筋与栓钉嵌入混凝土板中,使得钢筋、栓钉可以与混凝土板协同工作,模型中主要采用的接触设置如表8所示。

表8 模型接触关系Table 8 Model contact relations

4.2 UHPC材料本构

采用塑性损伤模型模拟混凝土由损伤所引起的退化行为,根据ABAQUS用户手册,对其塑性参数进行设置,如表9所示。

表9 塑性参数Table 9 Plasticity parameters

UHPC受压本构采用单波提出的拟合公式[17]:

(9)

式中:fc为抗压强度,fc=152 MPa;x=ε/ε0,ε为应变,ε0为峰值应变,取3 500×10-6;a为初始切线模量和峰值割线模量的比值,a=1.09;b为试验拟合参数,b=2.41[8]。

UHPC的受拉应力-应变曲线采用张哲等提出的UHPC双线性受拉应力-应变关系[18]:

(10)

式中:fct为应变硬化阶段平均应力,取fct=8 MPa;εca为弹性阶段峰值应变,取εca=2×10-4;εpc为极限应变,取εpc=1.941×10-3。

UHPC的受拉、受压损伤因子通过将式(9)、式(10)中的应力-应变关系代入式(11)中计算[19]:

(11)

4.3 有限元分析结果

4.3.1荷载-挠度曲线

图17为3根梁试件的试验值与模拟值荷载-挠度对比曲线,由图可知,其试验值与模拟值拟合较好。在裂后弹性阶段,试件刚度的试验值普遍小于模拟值,原因是在ABAQUS模拟中,将翼板中的普通混凝土层与UHPC层作为整体进行分析,不考虑两者之间的相对滑移,而试验过程中,可以观察到交界面处滑移裂缝的产生,因此,试验梁的裂后刚度试验值要小于模拟值。

图17 3根试件梁荷载-挠度曲线对比Fig.17 Comparisons of load-deflection curves of three specimens

4.3.2裂缝分布

ABAQUS塑性损伤模型无法模拟翼板的开裂,但可以通过拉伸损伤来近似地表征裂缝的分布。如图18、19所示,其裂缝的分布与实际测量得到的裂缝分布规律相近。

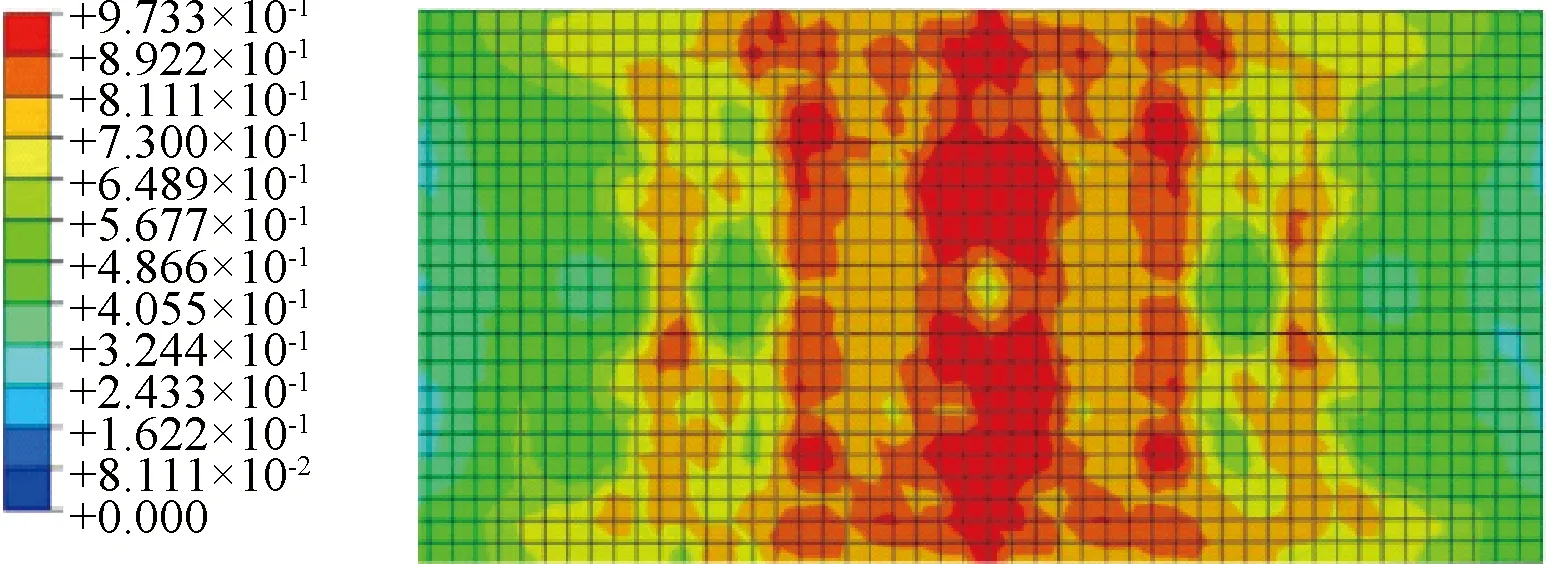
图18 SUCB-2拉伸损伤应变云图Fig.18 Strain cloud diagram of tensile damage of SUCB-2

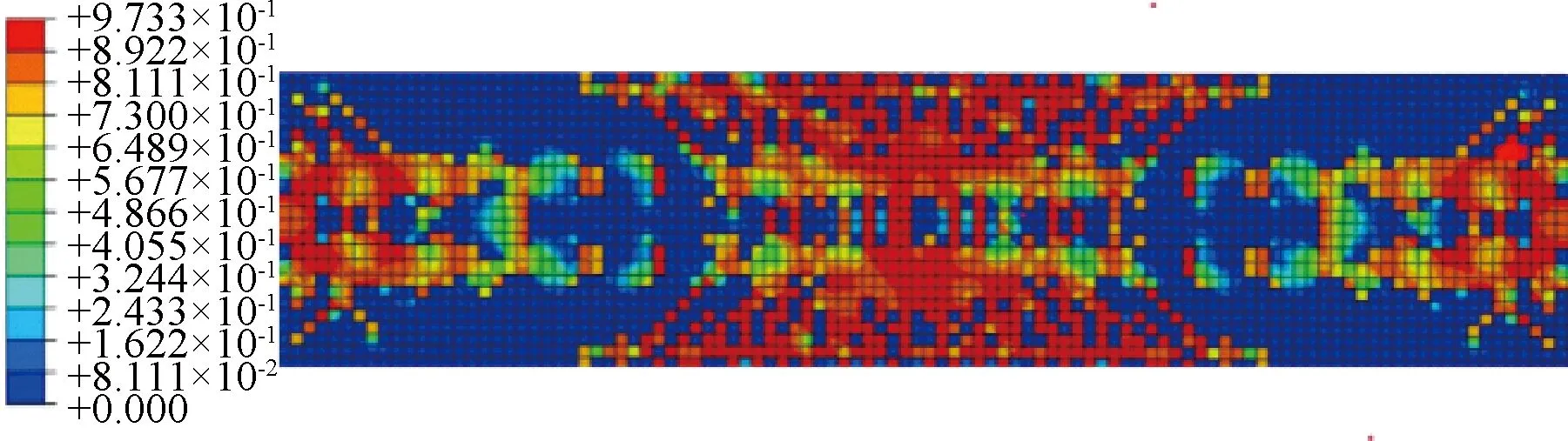
图19 SUCB-2底板拉伸损伤云图Fig.19 Tensile damage cloud image of base plate of SUCB-2

5 结 论

1)UHPC与NC材料具有良好的黏结性能,滑移裂缝出现较晚,仅在0.93fu处产生第一条滑移裂缝;而普通混凝土之间的黏结性能较差,第一条滑移裂缝出现在0.32fu处,且UHPC组合梁的滑移要明显小于普通混凝土组合梁。

2)相同配筋率下,相比于普通混凝土翼板,采用UHPC翼板其开裂荷载、屈服荷载以及极限荷载分别提高了74.6%、11.3%、1.5%,裂前刚度提高了8.7%,裂后刚度提高了22%。当配筋率从1%提高到2%时,其开裂荷载、屈服荷载、极限荷载提升相对较小,分别为11.8%、2.2%、3.3%,裂前刚度提高了1倍,裂后刚度提高33.7%。因此,配筋率对于组合梁的刚度影响较为显著。

3)基于截面平衡条件、平截面假定以及材料本构关系建立了UHPC-窄幅钢箱组合梁的受弯承载力计算模型,计算值与试验值吻合较好。

4)采用ABAQUS有限元软件建立了UHPC-窄幅钢箱组合梁分析模型,将模拟结果与试验数据进行对比,所建模型可较为准确地反映组合梁的受力特点。