钢骨不锈钢管超高性能混凝土柱轴压性能研究*
2023-07-26刘子丹焦文帅杜国锋
刘子丹 焦文帅 程 展 杜国锋
(1.长江大学城市建设学院, 湖北荆州 434000; 2.中梁控股集团有限公司, 上海 200333)
钢管混凝土柱因其强度高、延展性好、施工方便、抗震性能好等特点,在国内外超高层建筑、工业建筑和桥梁工程中得到广泛应用[1]。但传统钢管混凝土柱耐腐蚀性差,很难在海洋环境和腐蚀环境中应用。不锈钢因其较高的强度、较好的耐腐蚀性和耐火性,在特殊环境中的应用受到关注。国内外研究成果表明,用不锈钢替换钢管混凝土柱的外包钢管可以明显改善其力学性能和抗腐蚀能力[2-7]。当面临腐蚀环境时,不锈钢管混凝土柱具有更长的使用寿命和更低的维护成本。近年来,众多学者对不锈钢管混凝土柱展开了研究。代鹏等对奥氏体型和双相型的不锈钢管混凝土进行了轴压试验[8],结果表明:不锈钢管与核心混凝土协同工作良好,两者均有较高的极限承载力和变形能力。马国梁试验成果显示出不锈钢管混凝土柱具有较强的后期承载力和良好的变形性能[9]。文献[10-11]对圆不锈钢管混凝土柱进行了数值模拟,探究了径厚比、混凝土强度和不锈钢管等参数对其力学性能的影响。
由于不锈钢材价格较高,导致不锈钢管混凝土柱的应用受到一定限制。因此,有必要在不降低结构承载力的前提下,通过改变内填材料来减少不锈钢材的使用量。目前,许多研究都集中在将钢筋混凝土填充到不锈钢管柱中以改善其力学性能。Patel等通过试验和有限元分析指出,圆形混凝土填充双金属钢管(外侧为不锈钢,内侧为碳钢)柱与不锈钢管混凝土柱和钢管混凝土柱相比,强度更高,成本更低,并给出了相应的极限承载力预测模型[12]。乔崎云等对6个薄壁不锈钢管混凝土组合短柱进行了试验[13],结果表明不锈钢管-钢骨混凝土柱具有很高的承载力和较强的延性。
随着超高层结构的发展,钢管混凝土结构需要向更高承重、更优性能和更小截面发展,因此,提升普通混凝土性能成为必然。近年来,高性能混凝土、超高强度混凝土和超高性能混凝土不断发展。相比而言,超高性能混凝土具有较高的抗压强度、韧性和耐久性[14],将其作为核心混凝土,不仅可以进一步提高柱承载力,还可以大大减少试件的截面尺寸和自重,降低施工成本。但文献[15-16]研究成果指出,随着核心混凝土强度的提高,试件脆性会变大。为解决这一问题,本文试图通过内置钢骨来提高柱的刚度和延性。为此,提出了一种新型的内置型钢的不锈钢管超高性能混凝土柱(steel-reinforced ultra-high performance concrete-filled stainless steel tubular,简写为SRUFSST;当无内置型钢时,构件缩写为UFSST)。为研究不锈钢管、型钢、超高性能混凝土三者对柱整体性能的影响,以及三者间的协同工作性能,通过试验分析了径厚比(D/t)、长径比(L/D)和含骨率(ρ)对试件轴向压缩性能的影响。通过ABAQUS进行了有限元分析,根据试验和数值模拟结果,提出了SRUFSST柱的极限承载力预测模型,为此类结构的工程应用提供了参考。
1 试验设计
试验拟定参数为长径比(L/D)、径厚比(D/t)和含骨率(ρ),共设计了14个试件,包括6个短柱和8个中长柱,试件截面如图1所示。长径比(L/D)共有2.78、5、6.67和8.33 4种,为避免试件整体屈曲对轴向压缩试验的影响,取短柱和中长柱的长径比(L/D)限值为4[17],其中L为试件的高度,D为不锈钢管的外径。外包结构选取外径为180 mm的无缝不锈钢管,壁厚t分别为2 mm、3 mm和4 mm,相应的径厚比(D/t)为90、60和45。内置钢骨采用I10、I12和I14工字钢,试件含骨率(ρ)分别为5.62%、7%和8.45%,ρ由ρ=Ass/Asc得到,其中Ass和Asc分别为钢骨和试件的横截面积。各试件参数如表1所示。
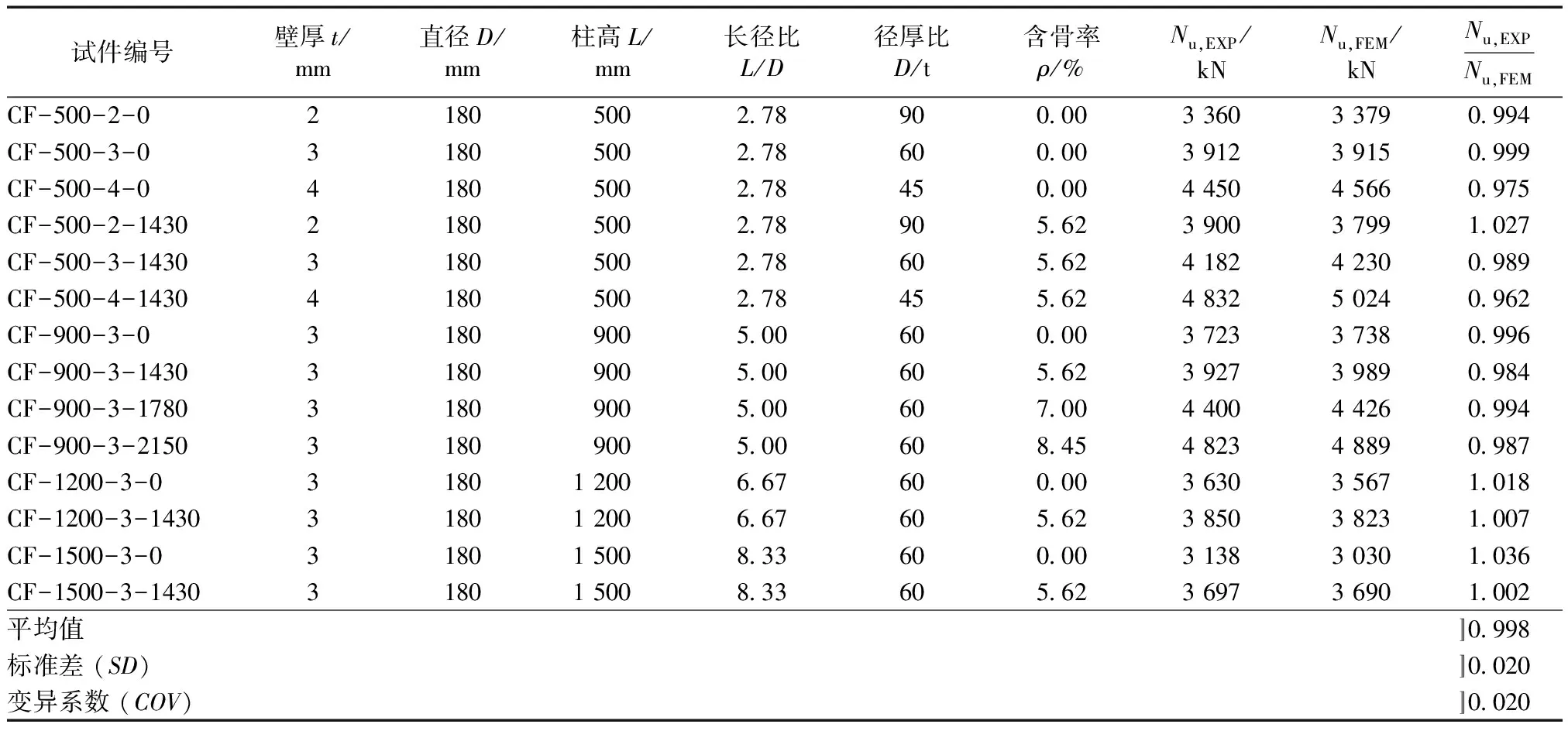
表1 试件参数Table 1 Parameters of specimens
1.1 材料性能
钢管选用奥氏体304级不锈钢,工字钢为Q235级碳素钢。根据GB/T 228.1—2021《金属材料 拉伸试验 第1部分:室温试验方法》[18],进行钢材拉伸试验,试验结果如表2所示。超高性能混凝土(UHPC)配合比如表3所示,水泥为P·O·52.5的普通硅酸盐水泥,掺合料分别为S95级矿粉和优质微硅粉。细骨料选用双级配石英砂。为了改善UHPC的流动度,加入胶凝材料重量3%的高性能聚羧酸减水剂。此外,使用长径比67、抗拉强度2 850 MPa的镀铜微丝钢纤维。在浇筑试件时,同时制备尺寸为100 mm×100 mm×100 mm的立方体试块,在与试件相同环境下养护28 d。按T/CECS 10107—2020《超高性能混凝土(UHPC)技术要求》[19],测得立方体抗压强度fcu为131 MPa,立方体强度与圆柱体强度换算系数取0.875[20]。

表2 钢材力学性能Table 2 Mechanical properties of steel

表3 超高性能混凝土配合比Table 3 Mix ratios of ultra high performance concrete kg/m3
1.2 加载制度与测点布置
试验在5 000 kN的液压伺服试验机上进行,试验布置如图2a所示,中长柱试验时,在压力机顶板和底板处加装铰支座。试验采用分级加载制度,度,0.65Fu(Fu为构件预估峰值荷载)之前每级200 kN,0.65Fu到0.8Fu之间每级100 kN,此后每级50 kN,每级荷载均保持5 min。正式加载前,对试件物理对中和几何对中,并以0.1Fu进行预加载。当试件轴向变形过大或荷载-位移曲线下降至0.6Fu时,停止加载。为测量试件在荷载下的应变,分别在不锈钢管以及内置钢骨的中部、1/3和2/3处布置应变片,测点布置如图2b所示。
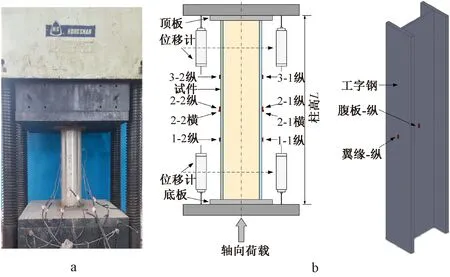
a—试验布置; b—测点布置。图2 试验和测点布置示意Fig.2 Diagrams of experiment set-up and measuring points layout
2 试验结果分析
2.1 破坏形态
短柱破坏形态如图3和图4a、4b所示,UFSST柱的破坏集中在试件两端。由于端部效应,试件在轴向荷载作用下柱端发生鼓曲,随着荷载的提高,在核心UHPC内部形成了一道贯穿试件的剪切滑移面,属于剪切破坏。SRUFSST柱的破坏出现在柱中和末端的受压侧,核心UHPC被压碎,钢纤维被拔出,随着荷载的增加,裂纹由端部向中部发展,形成了两道相交的剪切滑移面,属于双重剪切破坏。图5显示了中长柱在轴向荷载下的破坏形态。两类试件整体均产生明显弯曲,并伴随着横向偏转,柱中不锈钢管局部鼓曲明显,由于二阶效应影响,试件最终在轴向荷载和附加弯矩的共同作用下发生压弯破坏。图4c为中长柱拆解破坏示意,可明显观察到试件受压侧核心UHPC被压坏,受拉侧沿着轴向呈现许多近似水平的拉伸裂缝。此外,SRUFSST柱的破坏位移较UFSST柱更大,不锈钢管向外鼓起的时间也有所延迟。上述结果表明,不锈钢管、钢骨和UHPC的有益组合极大地增强了试件的轴向刚度,提高了抵抗变形的能力。
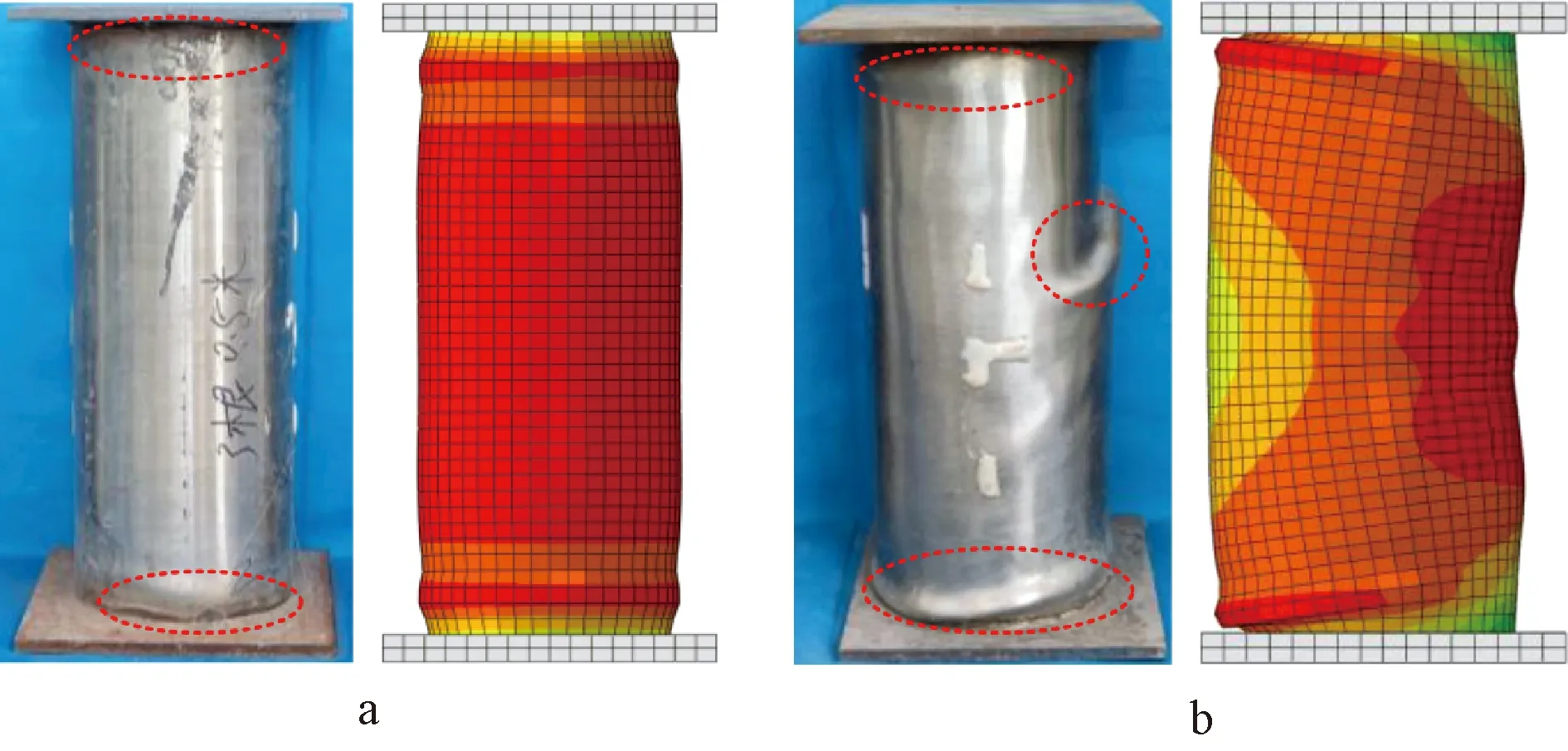
a—CF-500-3-0; b—CF-500-3-1430。图3 短柱破坏形态Fig.3 The failure modes of short columns

a—UFSST短柱; b—SRUFSST短柱; c—中长柱局部。图4 核心UHPC破坏形态Fig.4 The failure modes of core UHPC
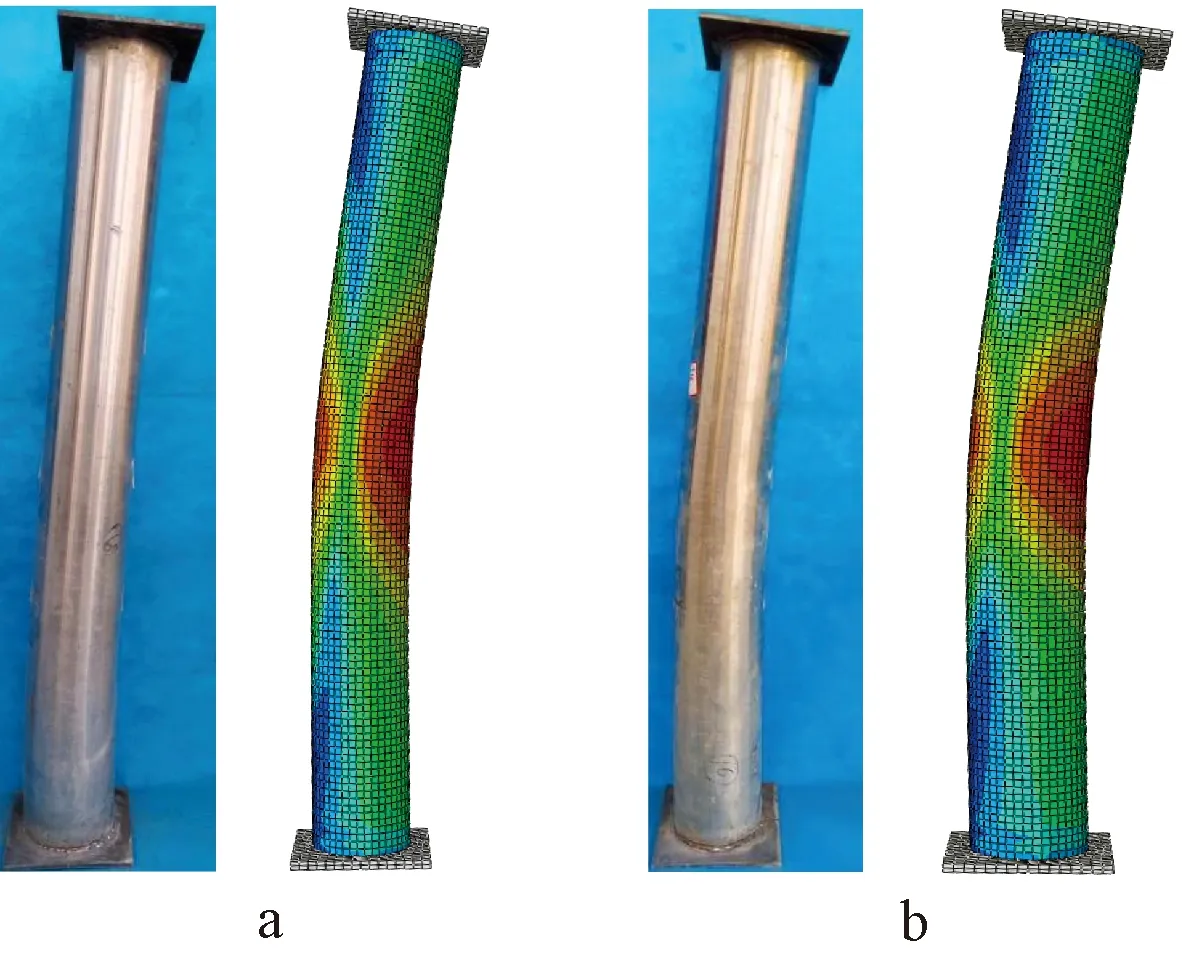
a—CF-1500-3-0; b—CF-1500-3-1430。图5 中长柱破坏形态Fig.5 The failure modes of mid-length columns
2.2 荷载-位移曲线
试验荷载-位移曲线如图6所示。曲线开始均呈线性增长趋势,试件处于弹性阶段,核心UHPC、不锈钢管和钢骨协同工作良好。在达到峰值荷载后,曲线逐渐下降,随着荷载增加,试件纵向位移增长速率持续加快,超高性能混凝土对不锈钢管挤压作用加强,最后,试件仍存在一定的残余强度。这是因为不锈钢管对开裂的核心混凝土仍存在约束作用,不锈钢管和钢骨也均处于应变硬化阶段。

a—径厚比(无钢骨试件); b—径厚比(内置钢骨试件); c—长径比(内置钢骨试件); d—长径比(无钢骨试件); e—含骨率。图6 不同参数试件荷载-位移曲线Fig.6 Load-displacement curves for specimens with different parameters
2.3 参数分析
2.3.1径厚比
不同径厚比条件下试件的荷载-位移曲线如图6a、6b所示,当径厚比减小时,试件的极限承载力、初始刚度和残余强度显著提升,刚度软化速度变缓。径厚比由90减小到60和45时,UFSST柱的极限承载力分别增加了16.43%和32.44%,SRUFSST柱极限承载力分别提高了7.23%和23.90%。这是由于管径一定时,随着壁厚的增加,核心UHPC受到的横向约束效应逐渐增强,抵抗开裂的能力提升。同时,随着钢管厚度增大,其自身承载能力也随之增强。
2.3.2长径比
不同长径比下的试件荷载-位移曲线如图6c、6d所示。随着长径比增大,试件的极限承载力、初始刚度和残余强度变小,下降段曲线陡峭趋势明显,试件延性降低。长径比由2.78增大至5.00、6.67和8.33时,SRUFSST柱的极限承载力分别降低了6.10%、7.94%和11.60%;UFSST柱的极限承载力降低了4.83%、7.21%和19.79%。当长径比增大时,试件的二阶效应愈发严重,相应的附加弯矩和侧向挠度变得更大,导致试件在纵向轴力和弯矩的共同作用下发生失稳破坏。
2.3.3含骨率
不同含骨率下的试件荷载-位移曲线如图6e所示。SRUFSST柱的极限承载力、初始刚度和残余强度随着含骨率的增大而增加,下降段曲线更加平缓。随着含骨率增加,试件轴向刚度提升,从而抑制了核心UHPC内部微小裂缝的产生,此外,试件截面强度也得到了提高。含骨率由0.00%增大至5.62%、7.00%和8.45%时,试件极限承载力分别增加了5.48%、18.18%和29.55%。
2.4 荷载-应变曲线
试件的荷载-应变曲线如图7所示。在加载初期,各测点曲线均呈线性增长趋势,钢管与UHPC近似单独受力。随着荷载的增加,钢管横向应变相较于纵向应变增长速率有所加快,对核心UHPC的包裹作用逐渐增强。此后纵向应变曲线进入非线性增长阶段,试件左右两侧测点处的纵向应变增加幅度有所不同。达到峰值荷载后,各测点应变增长速度明显加快,且横向应变的增长速率逐渐增大,表明UHPC在加载后期具有较大的膨胀变形,而不锈钢管在加载后期直至试件破坏都对核心UHPC提供了较强的横向约束力,使试件具有较好的变形能力。
为进一步研究SRUFSST柱在轴向荷载下的破坏机理,对试件各组件中截面的荷载-应变曲线进行分析。从图8a中可以看出,试件长径比越大,内置钢骨延性越低。这是由于二阶效应的影响,较大的长径比在轴力下产生了更大的附加弯矩,试件在两者共同作用下发生失稳破坏。如图8b~8d所示,在弹性阶段,钢骨和管壁的应变呈现相同的发展趋势,说明两者的协同工作性能很好。在弹塑性阶段,钢骨腹板的应变增长速率比翼缘和不锈钢管更快,当腹板达到屈服应变时,翼缘和不锈钢管仍处于载荷的上升段,随后翼缘和不锈钢管分别达到屈服状态。
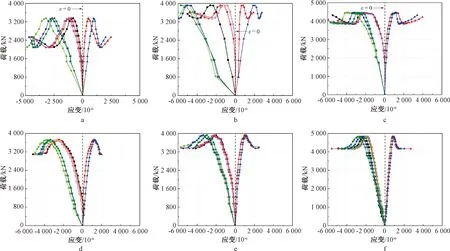
a—CF-500-2-0; b—CF-500-3-0; c—CF-500-4-0; d—CF-900-3-0; e—CF-900-3-1430; f—CF-900-3-2150。3-1纵; 2-1纵; 2-1横; 1-1纵; 3-2纵; 2-2纵; 2-2横; 1-2纵。 图7 试件荷载-应变曲线Fig.7 Load-strain curves for specimens
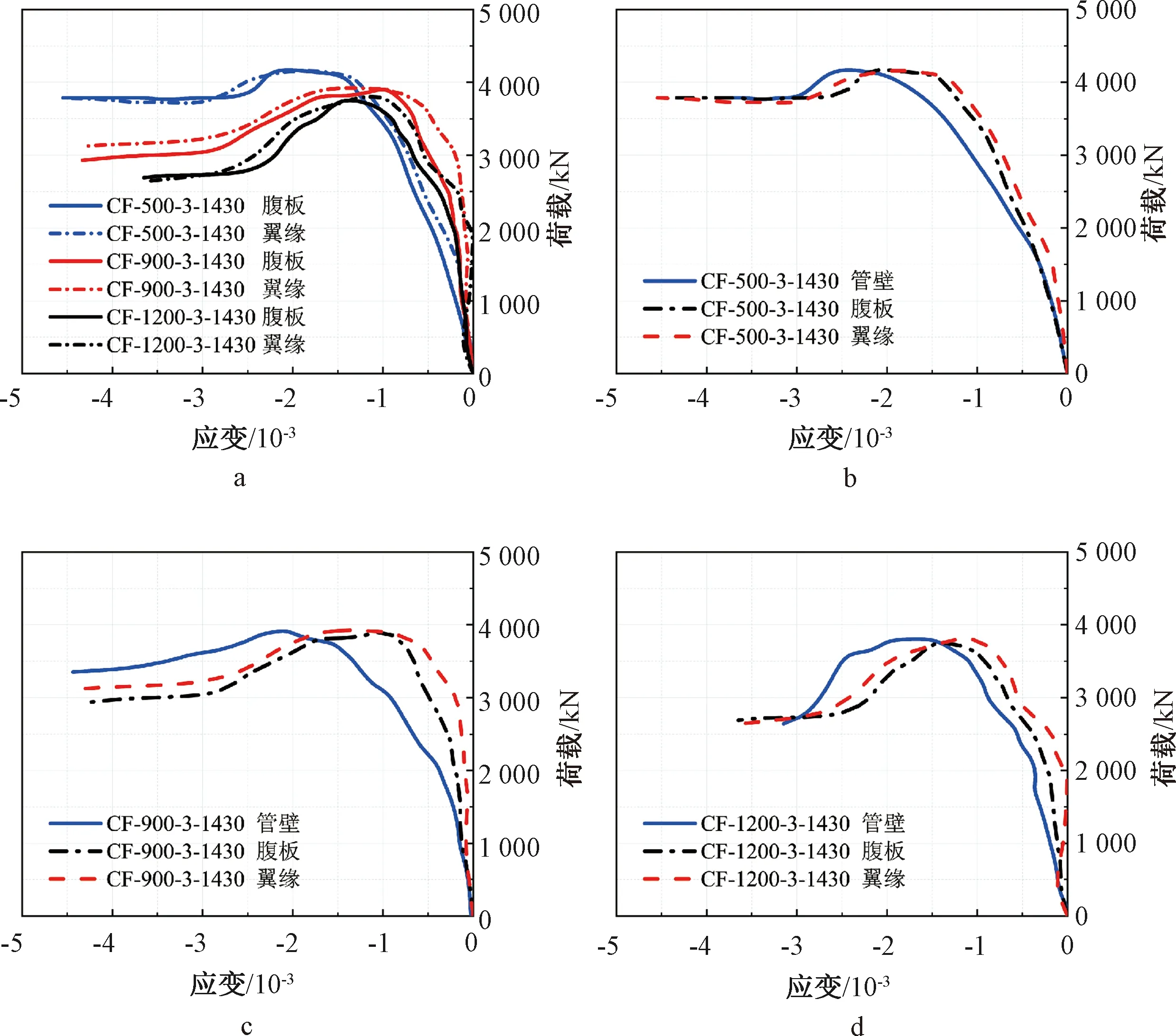
a—不同长径比试件; b—CF-500-3-1430; c—CF-900-3-1430; d—CF-1200-3-1430。图8 各组件中截面的荷载-应变曲线Fig.8 Load-strain curves for the middle section of each component of specimens
3 有限元分析
为了进一步揭示SRUFSST柱在轴向荷载下的力学性能,在考虑试件几何初始缺陷和不锈钢管横向约束效应下,建立了有限元模型。
3.1 材料属性
3.1.1不锈钢材料
Ramberg于1943年提出了不锈钢材的应力-应变模型[21],Eurocode 3 Part 1-4[22]在前者基础上进行了修正,提出了两阶段不锈钢钢材应力-应变关系模型:
(1)
式中:σ0.2和σu分别为不锈钢的名义屈服强度和峰值强度;E和εu分别为不锈钢的弹性模量和峰值应变,计算式为εu=1-(σ0.2/σu);Ey=E/[1+0.002n·(E/σ0.2)]是应力达到σ0.2时的切线模量;系数n是应变硬化指数,由n=ln(20)/ln(σ0.2/Rp0.01)得到,其中Rp0.01是残余应变为0.01%时的应力值;系数m=1+3.5σ0.2/fu。
3.1.2约束混凝土
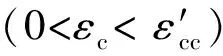
(2)
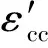
(3)

(4)
式中:fcr为核心混凝土的残余强度;εci为下降段曲线反弯点对应的应变值,由Ahmed等提出[26],如下所示。
Lim和Ozbakkaloglu根据众多试验结果回归分析得到了εci的计算公式[25],Ahmed等在研究的基础上进行了修正,引入参数γc来描述εci计算式[26]:

(6)
式中:γc为核心混凝土尺寸缩减因子,Liang通过钢管混凝土柱的试验结果给出了计算式[27]如下:
(7)
其中Dc=D-2t
式中:Dc为核心混凝土的直径;D和t分别为不锈钢管直径和厚度。
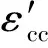
(8)
(9)
(10)
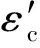
(11)
式中:vs和ve分别为不锈钢管在无填充和有填充UHPC时的泊松比,vs=0.5,Tang等给出了ve的计算公式[31]如下:
(12)
(13)
UHPC塑性参数Kc为0.8,膨胀角ψ为40°,偏心率为0.1,fb0/fc0(f60、fco分别为初始等效双轴抗压屈服应力和初始单轴抗压屈服应力)的值为1.033,混凝土的黏性系数为0.001[32]。
3.1.3钢 骨
工字钢采用Han等提出的二次塑流模型[33],应力-应变关系曲线一般可分为五个阶段,其中fp、fy和fu分别为钢材的弹性极限、屈服强度和抗拉强度,应力-应变关系如下:
(14)
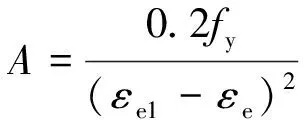
B=2Aεe1
式中:Es和fy分别为钢材的弹性模量和屈服强度;εe,εe1,εe2,εe3分别为钢材应力-应变曲线不同阶段的临界应变点,εe=0.8fy/Es,εe1=1.5εe,εe2=10εe1,εe3=100εe1。
3.2 数值模型
核心混凝土、工字钢和加载板均采用六面体单元(C3D8R)建模,不锈钢管为壳单元(S4R),经网格敏感性分析对试件进行网格划分,如图9所示。试件两端加载板均定义为刚体,短柱顶板约束除Y轴位移以外的所有自由度,底板采用完全固接。对于中长柱试件,除顶板Y轴位移外,上下加载板均采用铰接。不锈钢管与核心混凝土之间的接触为表面与表面接触,取库伦摩擦系数为0.25[34]。钢骨内置于核心UHPC内,仅考虑两者之间的黏结作用,不考虑相对滑移,不锈钢管与上下加载板的连接方式为壳-实体耦合。将试件一阶屈曲模态乘以一个缩放因子作为初始几何缺陷,缺陷大小取值为L/2 000[35]。此外,模型采用位移加载制度,加载速率为0.5 mm/s。

图9 SRUFSST网格示意Fig.9 Schematic diagram of SRUFSST meshes
3.3 试验有限元对比
试验和有限元荷载-位移曲线对比如图10所示。曲线上升段、下降段和残余强度均吻合较好,特征基本保持一致。由表1可知,Nu,EXP/Nu,FEM的均值为0.998,标准差和变异系数均为0.020。图3和图4比较了短柱和中长柱在轴向荷载下试验和有限元的破坏形态,短柱吻合了柱端和柱中的屈曲模式,中长柱也保证了柱中的横向偏转和局部鼓曲,均与试验结果较为一致。对比结果表明,提出的数值模型对SRUFSST的轴压模拟可靠度较高,并为承载力提供了较准确的预测。
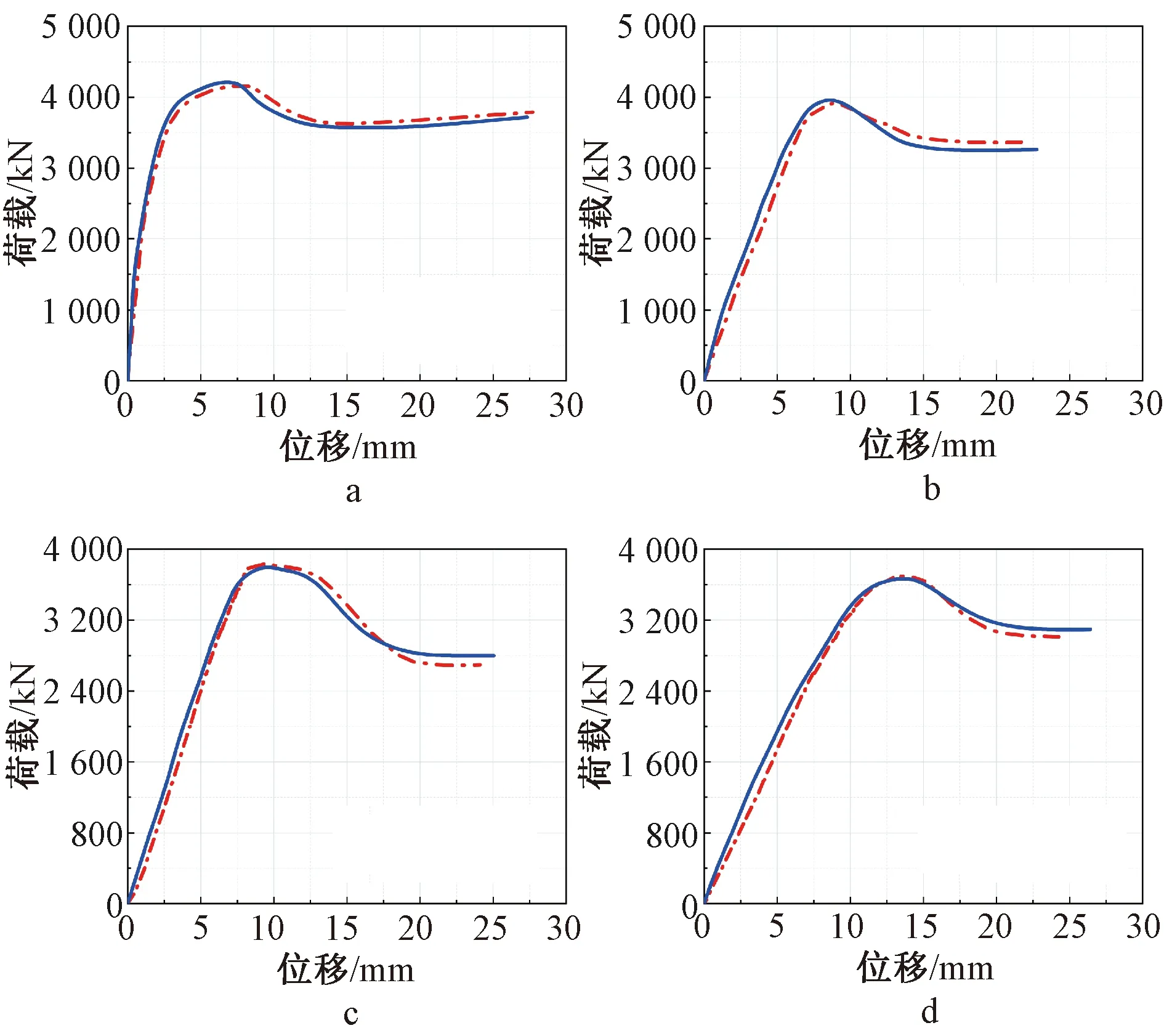
a—CF-500-3-1430; b—CF-900-3-1430; c—CF-1200-3-1430; d—CF-1500-3-1430。试验实测; 数值模拟。图10 试验与数值模拟荷载-位移曲线对比Fig.10 Comparisons of load-displacement curves between experimental results and numerical simulation ones
3.4 参数拓展分析
通过试验对试件的径厚比、长径比和含骨率进行了参数分析。为了更全面地探究各参数对UFSST短柱的影响,基于上述经验证的数值模型,进行了核心UHPC强度和内置钢骨强度参数拓展分析,如表4所示。
表4 公式结果与试验和有限元分析结果的比较Table 4 Comparisons of formula results with experimental and finite element analysis results
3.4.1核心UHPC强度
核心UHPC的强度等级对试件荷载-应变曲线有显著影响,如图11所示。试件的极限承载力和残余强度随着核心UHPC强度的增大而提高,增长趋势如图12所示。由于极限承载力主要由约束混凝土提供,因此,随着强度的增加,核心UHPC贡献的承载力不断增大,从而试件极限承载力大幅提高。但是,核心混凝土强度的增加伴随着脆性的变大,导致试件在曲线下降段的斜率变大,刚度退化加快。

a—CF-500-3-1430; b—CF-900-3-1430。fcu=130 MPa; fcu=150 MPa; fcu=170 MPa。图11 不同UHPC强度试件的荷载-位移曲线Fig.11 Load-displacement curves of specimens with different core UHPC strengths
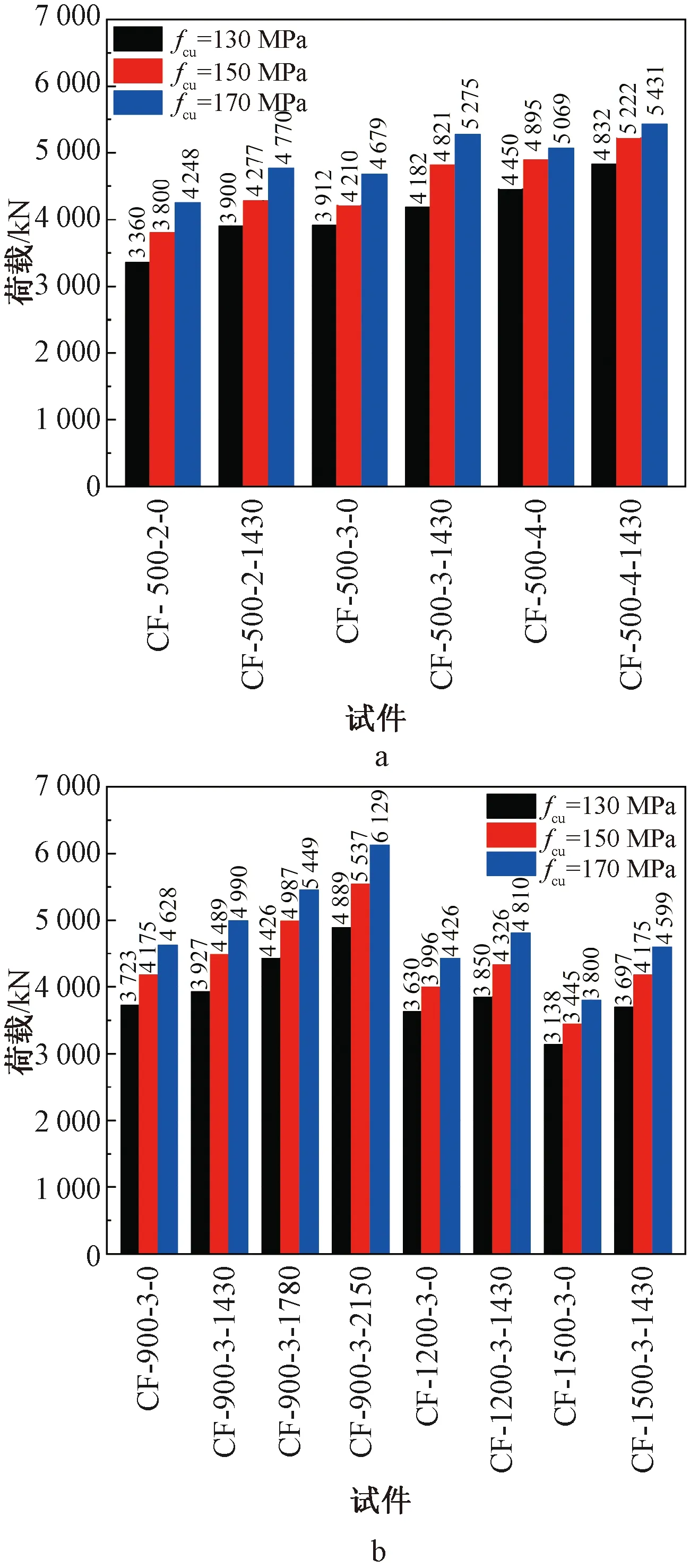
a—短柱试件; b—中长柱试件。图12 不同UHPC强度试件的极限承载力Fig.12 The ultimate bearing capacity of specimens with different core UHPC strengths
3.4.2内置钢骨强度
不同钢骨强度试件的荷载-位移曲线如图13所示,荷载增长趋势如图14所示。结果表明,随着钢骨强度提高,试件的极限承载力提高,残余强度也略有提高。这是由于截面尺寸一定时,试件的截面强度和轴向刚度随着内置钢骨强度的增大而增大,从而提高了试件的极限承载力。
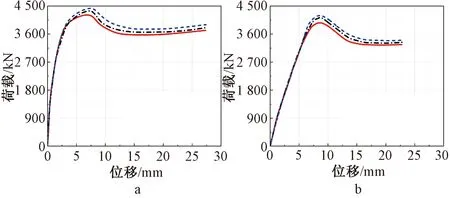
a—CF-500-3-1430; b—CF-900-3-1430。fsy=235 MPa; fsy=345 MPa; fsy=390 MPa。图13 不同钢骨强度试件的荷载-位移曲线Fig.13 Load-displacement curves of specimens with different steel profile strengths
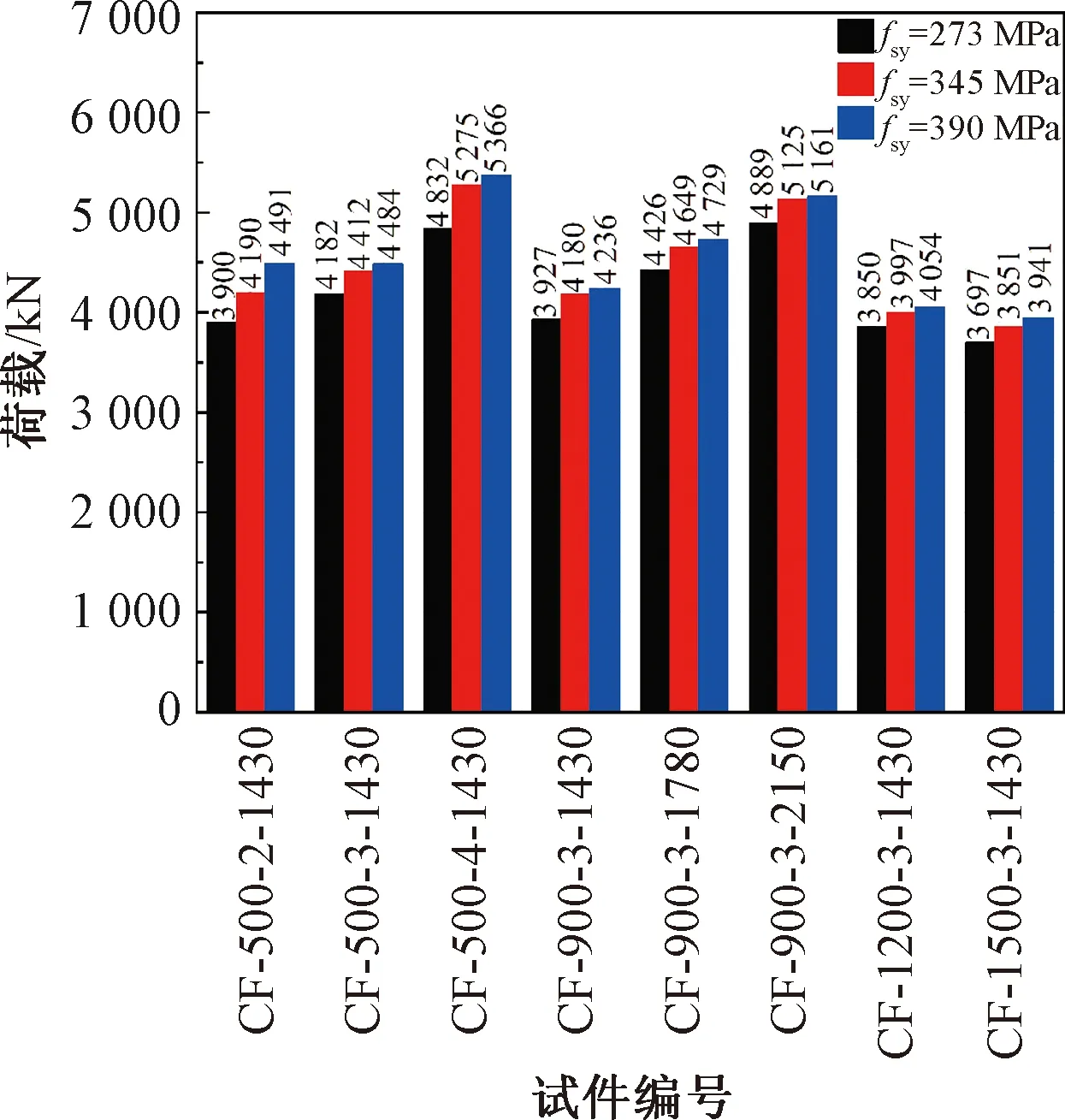
图14 不同钢骨强度试件的极限承载力Fig.14 The ultimate bearing capacity of specimens with different steel profile strengths
4 轴压承载力计算模型
目前,国内外研究尚无SRUFSST柱的极限承载力计算式。因此,根据叠加原理,将试件截面视为UFSST柱截面和钢骨截面的叠加。不锈钢管的横向约束使核心UHPC在轴向载荷下处于三轴应力状态,这大大增加了混凝土的峰值应力和峰值应变,UHPC的存在同时抑制了不锈钢管的局部屈曲,此外,内置钢骨也显著提高了试件的轴向刚度。因此,为了具体评估它们之间的积极作用,表现内置钢骨对UFSST柱极限承载力的影响,引入抗压指标SI和钢骨影响系数ξ,如式(15a)和式(15b)所示。
(15a)
(15b)
其中Nu,NOM=Asσ0.2+Acf′cc+Assfsy
式中:Nu,NOM为截面名义强度,显然,当Ass为0时,试件为UFSST柱;As和Ac分别代表不锈钢管和核心UHPC的横截面积;fsy为钢骨的屈服强度。假定SI与ξ存在线性关系,如式(16)所示,显然,当Ass为0时,SI等于1,此时极限承载力计算模型正好适用于UFSST柱。
(16)
式中:a为强度影响参数,根据短柱的试验及数值模拟结果进行回归分析得a=0.984 8。因此,联立式(15)~(16)得到SRUFSST短柱的极限承载力计算式,如式(17)所示。
(Asσ0.2+Acf′cc+Assfsy)
(17)
对于SRUFSST中长柱,为了考虑试件整体屈曲对极限承载力的影响,引入长径比折减系数φ,由SRUFSST短柱轴压承载力的计算式,导出SRUFSST柱的统一承载力计算模型,见式(18)。
Nu=φNu,DES_S
(18a)
(Asσ0.2+Acf′cc+Assfsy)
(18b)
式中:Nu,DES为SRUFSST轴压极限承载力预测值。按照短柱和中长柱的长径比限值,建立了折减系数φ的表达式如式(19)所示,其中β为长径比影响参数,根据中长柱试验及有限元结果回归分析得β=0.053。
(19)
将计算模型结果与试验及有限元结果进行对比分析,如表4和图15所示。结果表明,Nu,DES/Nu,EXP/FEM的平均值为0.989,标准差和变异系数均为0.041,说明提出的计算模型能够准确地预测SRUFSST柱的极限承载力,为该组合结构轴压力学性能的理论研究提供了参考。
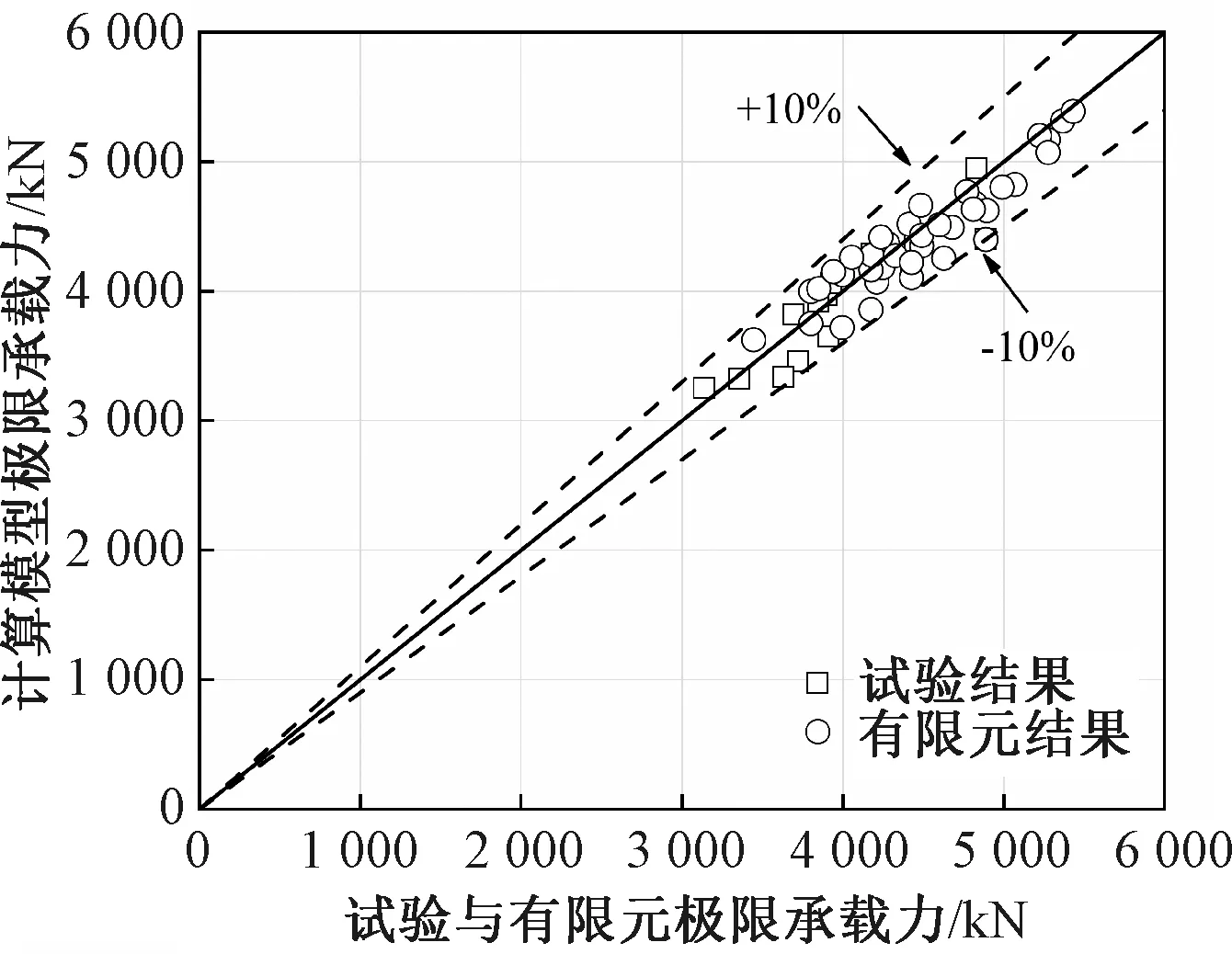
图15 计算模型验证Fig.15 Calculation model verification
5 结 论
对内置钢骨的不锈钢管超高性能混凝土柱轴压性能进行了研究,基于试验和有限元拓展结果,探究了试件的破坏模式,分析了不同参数对试件极限承载力、荷载-位移曲线的影响。得到以下结论:
1)随着径厚比减小,试件的极限承载力逐渐增大,荷载-位移曲线下降趋势逐渐变缓,延性得到改善;随着长径比增大,试件极限承载力明显降低,荷载-位移曲线下降段陡峭趋势明显,试件延性降低;随着含骨率增大,试件极限承载力随之增加,轴向刚度得到了一定程度的提高,试件延性随之提升。
2)试件极限承载力随着核心UHPC强度的提高而明显增大,但试件延性随之降低,刚度软化速率加快;随着钢骨强度提高,试件极限承载力增大,延性有所提升。
3)提出的承载力计算模型与试验和数值模拟结果吻合良好,为此类结构承载力评估、实际工程应用和相关规范修订提供了参考。
