海洋环境下混凝土结构耐久性寿命的概率分析*

2023-07-26郑少强陈业强刘荣桂王金元

工业建筑 2023年5期

郑少强陈业强刘荣桂王金元

(江苏大学土木工程与力学学院, 江苏镇江 212013)

0 引言

氯离子引起的钢筋腐蚀被认为是海洋环境中混凝土结构最重要的劣化机制之一[1-6]。钢筋腐蚀通常会导致混凝土保护层开裂、钢筋截面减少、钢筋与混凝土之间的黏结力丧失等,从而降低混凝土结构在海洋环境中的使用性能和承载能力[7-9]。以往对钢筋锈蚀起始时间的预测研究一般采用基于Fick第二定律的确定性方法[10-13]。然而,该确定性方法忽略了这些影响参数的概率特性,计算结果往往不是很合理[8],因此,有必要采用概率分析方法对混凝土结构的结构性能退化特性进行可靠性分析。

在工程实践中,环境作用的影响必须通过在暴露的混凝土中测量的氯化物侵蚀数据来量化[14]。在现有的研究中,影响参数的统计特性主要基于实验室试验或现场暴露试验的结果[15-18],而实际钢筋混凝土结构的长期现场结果较少[19-23]。王胜年等介绍了华东、华南等典型沿海地区开展海港工程混凝土结构原位调查的成果[14];Pang等对我国南海海岸的17座高桩码头进行耐久性调查[16]。这些参数需要根据实际海洋结构物的长期测量结果进行校准。

为此,结合连云港码头实际检测数据,着重讨论了模型参数的统计特性以及综合考虑耐久性保障率、最优可靠度以及可靠指标差值Δ三者耐久性概率分析方法。

1 基于时间的氯离子侵蚀模型

1.1 基本模型

氯离子在混凝土中的输运过程分为一系列基础物理化学过程,包括扩散、渗透、电迁移等[1]。其中,扩散方式过程被认为是最主要的传输方式[4]。在实践中,经常使用的简单模型为基于Fick第二定律,然而实际结构一般有多个暴露面,不能仅考虑一维模型[24]。本文采用二维的氯离子扩散模型[13]:

(1)

式中:C为距离混凝土表面x处的总的氯离子浓度;D为氯离子扩散系数;t为扩散时间;x和y为两个维度的扩散深度。

总的氯离子浓度C包括结合氯离子浓度和自由氯离子浓度[13],即:

C=Cb+Cf

(2)

式中:Cb为结合氯离子浓度;Cf为自由氯离子浓度。考虑混凝土中氯离子结合能力R[25]:

(3)

将式(2)和式(3)代入式(1)中可得:

(4)

同时,考虑到表观氯离子扩散系数的时间依赖性以及温度的影响[26],Da(t)可被表示为:

(5)

结合式(4)和式(5),为了简化计算,假定表面氯离子浓度Cs恒定且混凝土的初始材料中不含氯离子成分。混凝土中氯离子随时间相关的侵蚀模型可以用式(6)描述:

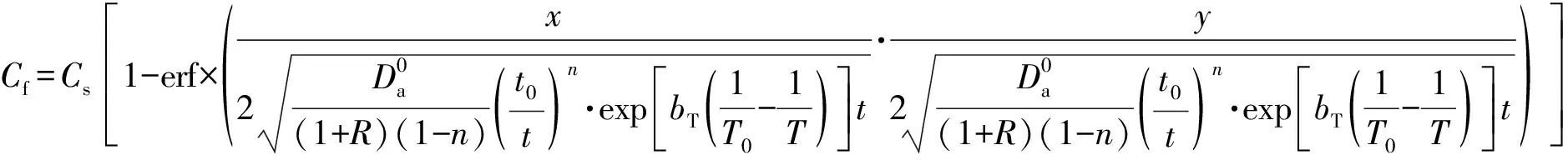
(6)

在混凝土结构耐久性寿命的概率分析中,用保护层厚度xd代替二维的扩散深度x和y。

1.2 耐久性极限状态

在2019年新发布的GB/T 50476—2019《混凝土结构耐久性设计标准》中,首次明确给出耐久性极限状态及定量设计方法的相关规定。将耐久性极限状态分为三类:钢筋开始锈蚀、钢筋适量锈蚀、混凝土表面轻微损伤。本文以钢筋锈蚀作为耐久性极限状态。

在内部钢筋表面氯离子浓度达到其阈值浓度时,混凝土结构发生腐蚀劣化[1]。因此,将钢筋刚刚达到脱钝时的状态视为耐久性极限状态。此时,耐久性极限状态功能函数G(X,t)如下:

G(X,t)=Ccr-Cf

(7)

根据式(5),海洋环境下混凝土结构耐久性极限状态的时变失效概率Pf(t)可以表示为:

Pf(t)=P{G(X,t)<0}=

P{C(xd,t)>Ccr}≤Ptarget

(8)

式中:Ptarget为预期的失效概率。

时变可靠指标与失效概率关系如下:

Pf=Φ(-β)

即:

β(t)=-Φ-1[Pf(t)]=Φ-1[1-Pf(t)]

(9)

式中:β(t)为t时的可靠指标;Φ-1[ ]为标准正态分布反函数。

1.3 失效概率的Monte-Carlo模拟

考虑到参数的分布随机性,很难通过解析法得出时变失效概率和可靠指标[8]。因此,本文借助于MATLAB软件,采用Monte-Carlo方法进行计算失效概率,通过MATLAB中的命令(-norminv)计算可靠指标。

Monte-Carlo方法的核心思想为随机抽样模拟,其准确性取决于试验的次数。本文采用了105次随机统计抽样,并采用文献[27]中数据,验证了所编写的Monte-Carlo模拟程序计算失效概率的准确性。图1为验证结果。

a—文献计算结果[27]; b—本文程序计算结果。1～4为文献[27]中4种情况。图1 Monte-Carlo模拟程序验证Fig.1 Monte-Carlo simulation program verification

2 参数统计特征

结合课题组在连云港码头的长期检测数据以及国内外相关的文献,对式(6)中参数的统计特性进行了分析。

2.1 连云港现场环境调查

连云港位于江苏省,处于季风海洋性气候地带,四季分明[28],雨量适中,年均降雨量852.8 mm,年平均气温14 ℃。连云港为不规则浅海半日潮港,平均涨潮历时5.62 h,平均落潮历时6.8 h,潮位相关数据以及海域海水的化学组成部分[29]见表1。

表1 连云港港区海水及潮位相关数据[29]Table 1 Sea water and tide level related data in Lianyungang Port area

2.2 混凝土保护层厚度xd

国内外统计结果见表2所列,其中,混凝土保护层厚度均为设计值,μxd为设计值均值。

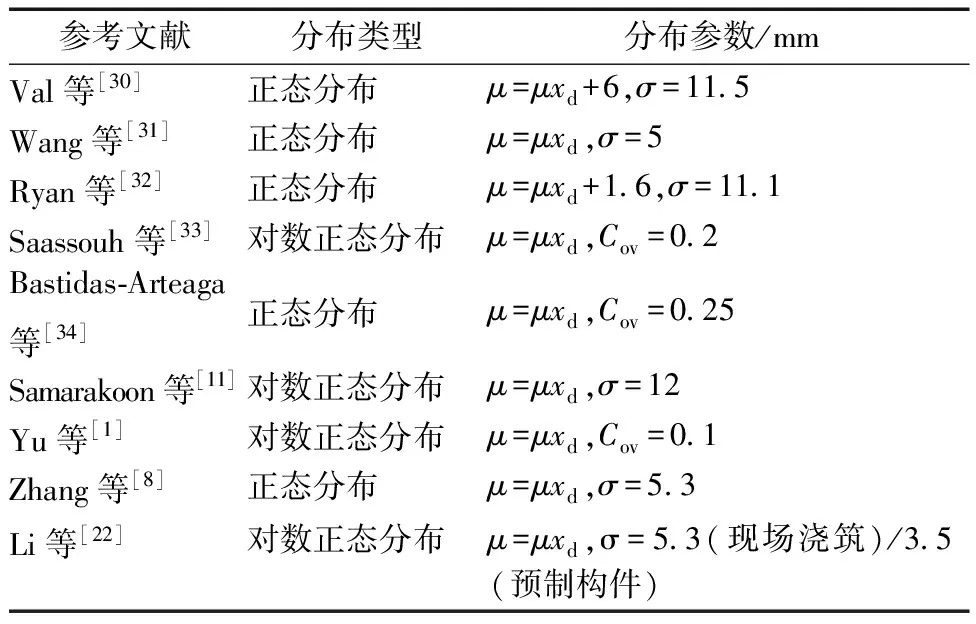
表2 保护层厚度统计结果Table 2 Statistical results of protective layer thickness

结合国内外文献,本文认为保护层厚度服从正态分布,均值为μ,变异系数Cov为0.1。

2.3 表面氯离子浓度Cs

表面氯离子浓度Cs不是直接测得的,而是通过方程(6)拟合回归得到的。将课题组在连云港码头进行的长期检测得到的氯离子数据进行拟合,得到不同区域的表面氯离子浓度,如图2所示。图中Cs取值为表面氯离子含量占混凝土质量的百分比。

Cs数据点。图2 表面氯离子浓度Fig.2 Surface chloride concentration

对不同环境下的表面氯离子浓度分布特征进行分析,大气区的Cs均值为0.50%,方差为0.01%,分别服从N(0.50,0.09)和LN(-0.70,0.20);浪溅区Cs均值为0.92%,方差为0.02%,分别服从N(0.92,0.13)和LN(-0.1,0.14);潮汐区Cs均值为0.87%,方差为0.01%。由此得到的概率密度图(PDF)、P-P图(Probability Plot)见图3～图5。

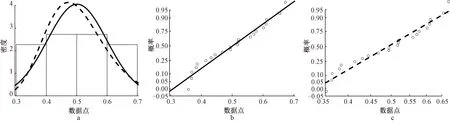
a—大气区PDF图; b—大气区正态分布P-P图; c—大气区对数正态分布P-P图。 Cs数据点;─正态分布拟合;┄对数正态分布拟合。图3 大气区统计分布Fig.3 Statistical distribution map of atmospheric area

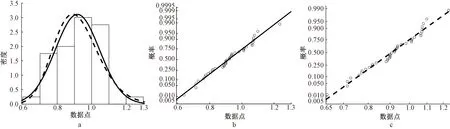
a—浪溅区PDF图; b—浪溅区正态分布P-P图; c—浪溅区对数正态分布P-P图。 Cs数据点;─正态分布拟合;┄对数正态分布拟合。图4 浪溅区统计分布Fig.4 Statistical distribution map of splash zone

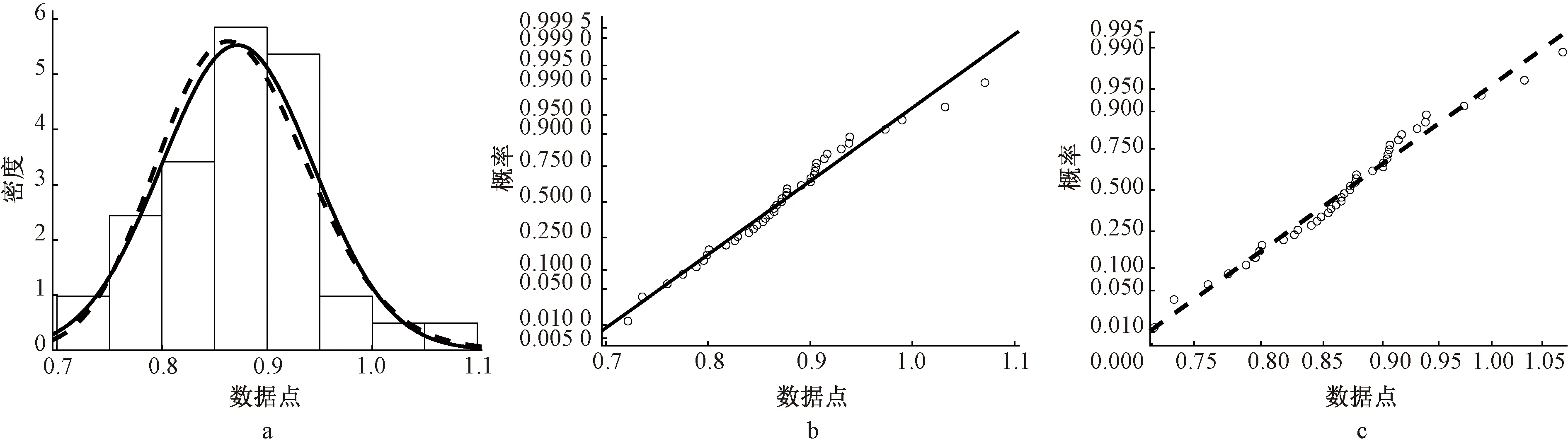
a—潮汐区PDF图; b—潮汐区正态分布P-P图; c—潮汐区对数正态分布P-P图。 Cs数据点;─正态分布拟合;┄对数正态分布拟合。图5 潮汐区统计分布Fig.5 Statistical distribution map of tidal area

结合图3～图5的P-P图可以得出:数据点与指定分布拟合图形为直线,服从指定的分布类型。将得到的两种分布类型同时进行Kolmogorov-Smirnov分布检验,结果皆为0,故接受原假设,可以认为连云港大气区Cs同时服从正态分布和对数正态分布。

水下区混凝土结构由于水中缺氧使锈蚀发展变得极其缓慢甚至停止[3],所以钢筋锈蚀危险性不大。同时没有充足的检测数据,本文不考虑水下区的参数统计特征。表3总结了水胶比w/b=0.4时,符合连云港码头Cs的统计特征。

表3 w/b=0.4时不同暴露环境下Cs统计特征Table 3 Cs statistical characteristics under different exposure environments when w/b=0.4 %

这里Cs同时服从正态分布和对数正态分布的差别很小,很大原因是参数统计量不够大。因此,本文将再结合国内外的参考文献确定Cs更优的参数分布。

国内外的研究结果[26,31-38]统计表明,表面氯离子浓度服从正态分布和对数正态分布,统计结果如表4所示。

结合国内外文献,认为表面氯离子浓度概率模型为正态分布,分布参数见表5。

表5 随机变量的统计特征Table 5 Statistical characteristics of random variables

2.4 临界氯离子浓度Ccr

国内外统计结果如表6所示。

表6 临界氯离子浓度统计结果Table 6 Statistical results of critical chloride concentration

本文中认为临界氯离子浓度概率模型为正态分布,分布参数见表5。

2.5 氯离子扩散系数

国内外统计结果如表7所示。

表7 氯离子扩散系数统计结果Table 7 Statistical results of chloride diffusion coefficient

2.6 龄期衰减系数n

国内外统计结果如表8所示。

表8 龄期衰减系数统计结果Table 8 Statistical results of age attenuation coefficient

本文采用Li龄期衰减系数n的分布类型和分布参数[19],认为龄期衰减系数服从正态分布。

2.7 参数统计

水胶比为0.4时,不同环境条件下随机变量的统计特性如表5所示。考虑到水下区氯离子侵蚀影响很小,这里并没有列出水下区的相关参数统计特性。其中,参数中常量R取1.15[13],T0取293.15 K[13],T取连云港地区年平均温度287.15 K[29]。

3 耐久性寿命的概率分析

GB/T 50476—2019中明确表示与耐久性极限状态相对应的结构设计使用年限应具有规定的保证率,并应满足正常使用极限状态的可靠度要求。根据正常使用极限状态失效后果的严重程度,可靠度宜为90%～95%,相应的失效概率宜为5%～10%。

同时,还应考虑结构的初期建设成本与后期维护成本的平衡问题。钟小平等[43]结合耐久性等级以及结构寿命期经济性,给出了不同耐久性极限状态目标可靠指标β。当耐久性等级为一级时,β=1.0;耐久性等级为二级时,β=1.5;耐久性等级为三级时,β=2.0。在本文的耐久性分析中,耐久性等级为一级,以β=1.0为最优可靠度进行分析。

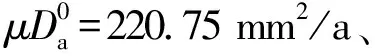
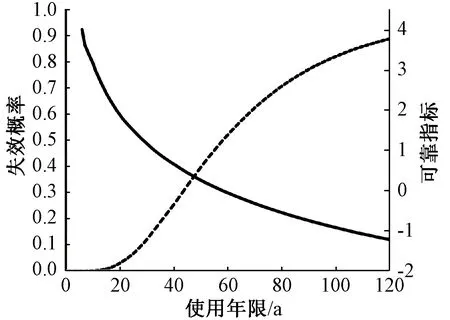
┄失效概率曲线;─可靠指标曲线图6 失效概率与可靠指标Fig.6 Failure probability and reliability index

由图6可得,当失效概率为10%时,对应的使用年限为29 a;考虑经济性时,可靠指标为1.0,对应的使用年限为34 a。

为了更好地进行耐久性分析,本文采用了失效概率为10%和可靠指标为1.0时对应的使用年限差值Δ。当失效概率为10%时,对应的可靠指标为1.26,则在Δ内可靠指标的斜率绝对值可表示为:

(10)

从式(10)中可以得出,随着Δ的增加,|k|降低,在差值Δ内可靠指标下降程度越缓,耐久性越好。同时Δ自身意义为从满足耐久性保证率到考虑经济性的最优可靠指标对应的年限差,这也在一定程度上反映了结构耐久性裕度。

a—失效概率曲线; b—可靠指标曲线。图7 μxd=50 mm时氯离子扩散系数的影响Fig.7 Influence of chloride diffusion coefficient when μxd=50 mm

3.1 μxd=50 mm

从图7中可以清楚地看出,氯离子扩散系数对失效概率及可靠指标的影响显著。当保护层厚度为50 mm时,随着氯离子扩散系数的增加,失效概率逐渐增加,可靠指标逐渐减少。腐蚀起始年限如表9所示。

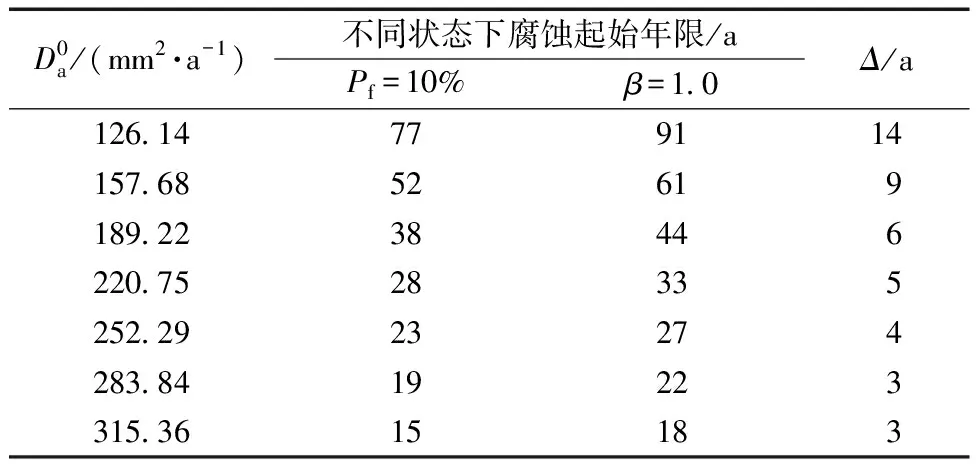
表9 μxd=50 mm时不同扩散系数下腐蚀起始年限Table 9 Corrosion initiation age under different diffusion coefficients when μxd=50 mm

从表9中Δ值的变化程度可以看出,随着氯离子扩散系数的增加,Δ不断减少。在氯离子扩散系数较低时,Δ降低程度较大;在氯离子扩散系数较高时,特别是超过220.75 mm2/a时,Δ降低程度变得很缓,且趋于稳定。这说明,随着氯离子扩散系数的增加,劣化速率越快,耐久性裕度不断降低。因此在设计时必须严格控制氯离子扩散系数,同时,在维护过程中也要根据检测、监测得到的实际情况选取相应的降低扩散系数的措施。

3.2μxd=60 mm

从图8中,可以看出,当保护层厚度为60 mm时,随着氯离子扩散系数的增加,失效概率逐渐增加,可靠指标逐渐减少。但对比图7和图8可知,随着保护层厚度从50 mm增加到60 mm时,总体上失效概率大幅降低,可靠指标大幅增加。腐蚀起始年限如表10所示。

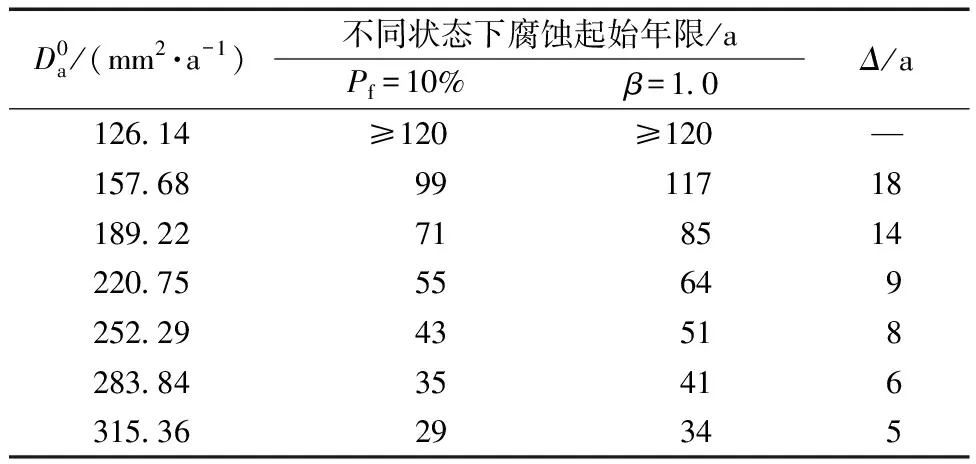
表10 μxd=60 mm时不同扩散系数下腐蚀起始年限Table 10 Corrosion initiation age under different diffusion coefficients when μxd=60 mm

a—失效概率曲线; b—可靠指标曲线。图8 μxd=60 mm时氯离子扩散系数的影响Fig.8 Influence of chloride diffusion coefficient when μxd=60 mm

从Δ值的变化程度可以看出,随着氯离子扩散系数的增加,Δ不断减少,且扩散系数较大时Δ降低程度比扩散系数较小时Δ降低程度低。这与μxd=50 mm时反映得特征相同。但将表9 与表10对比可知,Δ值明显增加,混凝土结构耐久性裕度得到提高。这说明保护层厚度的增加可以明显地降低氯离子扩散系数带来的影响,从而提高耐久性的保证率。从表9和表10中腐蚀起始年限的对比也可清晰地看出,虽然随着氯离子扩散系数的增加,腐蚀起始年限有明显的减少,但μxd从50 mm提升到60 mm时,总体的腐蚀起始年限得到了显著的增加,当扩散系数较低时更为明显。

3.3 μxd=70 mm

从图9中可以看出,当保护层厚度为70 mm时,随着氯离子扩散系数的增加,失效概率逐渐增加,可靠指标逐渐减少。腐蚀起始年限如表11所示。

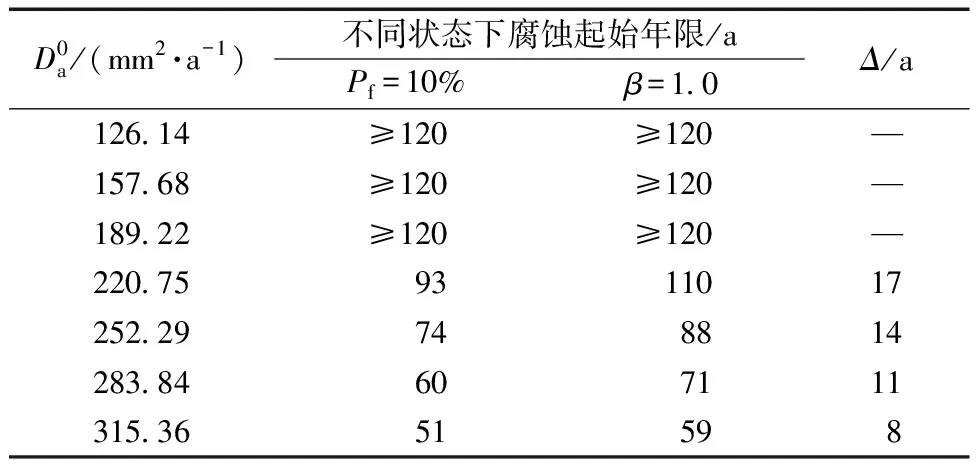
表11 μxd=70 mm时不同扩散系数下腐蚀起始年限Table 11 Corrosion initiation age under different diffusion coefficients when μxd=70 mm

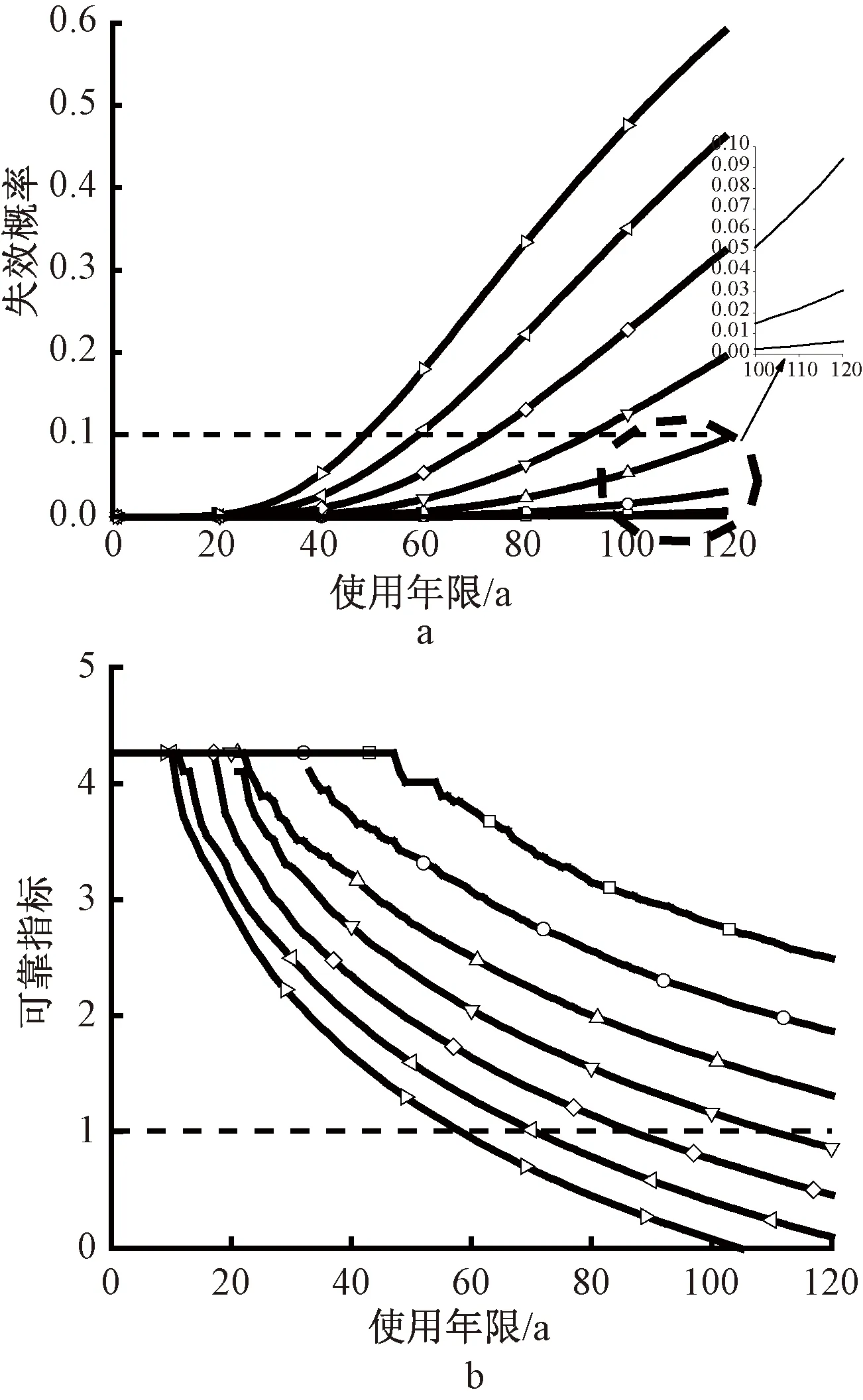
a—失效概率曲线; b—可靠指标曲线。图9 μxd=70 mm时氯离子扩散系数的影响Fig.9 Influence of chloride diffusion coefficient when μxd=70 mm

从Δ值可以看出,随着氯离子扩散系数的增加,Δ值不断减少,这说明可靠指标降低程度增大,耐久性裕度在降低。但将表9～表11综合对比可知,不同氯离子扩散系数对应的Δ值有很大的增加,相应地,腐蚀起始年限也得到了显著增加。

通过对图7～图9对比分析可以得出,氯离子扩散系数的增加会导致失效概率的显著增加,耐久性裕度降低。但随着保护层厚度的增加,混凝土的耐久性也是可以得到保证的。也就是说,在耐久性设计时,应该优先适当增加保护层厚度,其次是控制影响氯离子扩散系数的因素,如混凝土组分、水胶比等,并加以相应的防护措施(表面涂层、硅烷浸渍、阻锈剂等)。在混凝土使用过程中,应根据检测、监测情况,结合劣化程度选用合适的耐久性提升与修复措施(阴极保护、电化学除氯、微生物修复等)。