基于时变特性的多层脑网络拓扑属性分析及脑疾病分类

李涛, 邱震钰, 李瑶, 李囡, 李埼钒, 郭浩*

(1.太原理工大学信息与计算机学院, 太原 030024; 2.南昌理工学院计算机信息工程学院, 南昌 330044;3.太原理工大学软件学院, 太原 030024)

由于具有无创性和非侵入性的特点,功能磁共振成像技术目前已经被广泛应用于神经精神疾病的研究中[1]。研究人员常利用静息态功能磁共振成像技术通过血氧水平依赖信号表征脑区间自发的神经元活动,进而计算该信号的时间相关性表示脑区间的交互活动,以此构建脑功能网络来阐明疾病的病理机制从而实现分类[2-3]。

传统的脑网络认为静息态功能磁共振扫描期间功能连接是不变的[4]。但这在很大程度上忽略了大脑网络的动态特征,而最近的研究表明大脑是一个高度动态的网络系统[5-6]。基于此,研究人员提出了多层脑网络,用于表示随着扫描时间的推移脑区之间交互的时变特性[7-10]。

在已有的多层脑网络研究中,大多集中于对动态功能连接的探索,极少从网络的拓扑属性角度进行分析。但拓扑属性的引入有利于充分表征网络的结构信息,因而对精神疾病的诊断具有重要意义。目前针对多层网络拓扑属性的研究分为以下几种策略。①通过计算连接的连接将多层网络转变为单层网络,从而对单层网络的属性进行研究[11],但该方法本质上还是对单层网络属性进行分析;②将单层网络特定拓扑指标计算方法按照其特征扩展到多层网络,而此过程不适用于所有的单层拓扑指标到多层拓扑指标的转换,缺乏泛化性[12-13];③通过计算每层网络中拓扑指标的均值[6]或标准差[14-15]作为多层网络的拓扑指标值,这也是如今多层脑网络中最常用的一种计算拓扑指标值的方法。但是简单计算均值使得多个单层网络拓扑指标的极值无法得到有效利用,而这些值可能在一定程度上包含大脑的动力学信息[16];同时,单纯计算标准差的方法虽然可以反映多个单层网络中拓扑指标离散的绝对程度,但又会受到所有单层网络拓扑属性均值的影响[17]。

为了解决以上局限性,本研究在现有的利用均值和标准差计算多层网络拓扑属性的基础上,考虑到特定属性值及整体分布的影响,分别引入极差、相对极差、离散系数进行多视角多层网络拓扑属性的计算,从而实现对自闭症的分类。

首先,利用滑动窗口方法构建时变多层脑功能网络。其次,分别基于均值、极差、相对极差、标准差、离散系数计算多层网络的拓扑属性,并利用Kolmogo-rov-Smirnov(KS)非参数检验选取差异特征。然后,使用支持向量机(support vector machine, SVM)分别基于每种方法选取的差异特征及所有差异特征构建分类模型,比较不同方法的分类效果及研究中涉及的参数对分类性能的影响。最后,利用ADNI(Alzheimer’s disease neuroimaging initiative)数据集分析方法的可拓展性。相比于现有方法,本研究所提出的方法应取得更好的分类效果且具有较好的泛化性。

1 材料和方法

1.1 方法框架

基于时变特性的多层脑网络拓扑属性分析及脑疾病分类主要包括以下四个步骤。其具体流程如图1所示。

图1 方法框架Fig.1 Method framework

(1)数据获取和预处理。

(2)多层脑功能网络构建。利用滑动窗口方法构建基于时变特性的多层脑功能网络。

(3)特征提取。分别基于均值、极差、相对极差、标准差、离散系数视角计算多层网络的度、离心率、介数中心度。

(4)特征选择与分类。将非参数置换检验选取的每种视角下具有显著差异的特征及融合所有特征作为分类器的输入,并使用支持向量机对疾病进行分类。

1.2 数据集和预处理

1.2.1 数据获取

样本来源于自闭症脑影像数据共享中心(ABIDE, http://fcon_1000.projects.nitrc.org/indi/abide)中的纽约大学朗根医疗中心。各组数据排除标准为:①女性;②头动大于3 mm或转动大于3°。本研究最终纳入65例自闭症患者及76例健康对照。所有数据贡献者均通过机构审查委员会批准,且与受试者(或其监护人)签署知情同意书。所有被试详细信息如表1所示。其中,数据范围指最小值～最大值(平均值±标准差),ADOS-total表示自闭症诊断观察量表总分,P由双样本双尾T检验获得。

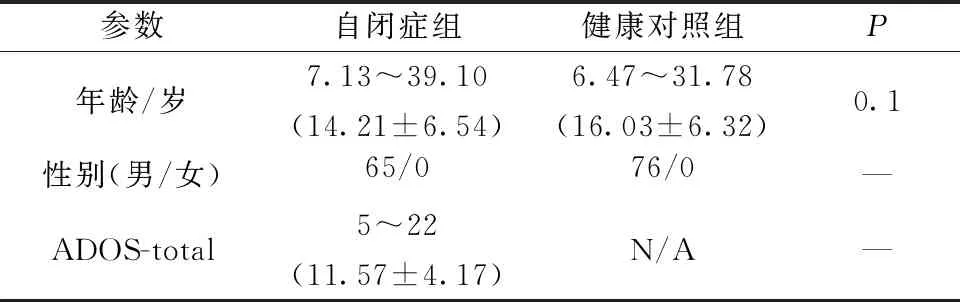
表1 被试的基本信息表

1.2.2 数据预处理

数据预处理使用GRETNA工具箱[18]进行,具体步骤包括:①去除前5个时间点数据;②时间层校正;③头动校正;④将图像配准至蒙特利尔神经研究所标准空间;⑤采用6 mm半高全宽的高斯滤波器对图像进行空间平滑;⑥去除协变量,如Friston 24头动参数、线性趋势、全局信号、脑白质及脑脊液信号;⑦带通滤波(0.01～0.1 Hz)。在校正过程中有3例自闭症患者和3例健康对照因头动大于3 mm或转动大于3°而被舍弃,不包含在最终的141名被试中。

1.3 多层脑功能网络构建

使用自动解剖标记模板[19]将大脑划分为90个脑区。把每个脑区作为脑网络中的一个节点,计算该脑区中所有体素在不同时间点上的血氧水平依赖信号的算术平均值来表示该节点的值。

采用滑动窗口方法[5, 20-21]构建时变多层脑功能网络,通过不同窗口内的时间序列构建单层网络,表示在一小段时间内脑区之间的功能连接,并引入层间连接表示不同层之间的脑区连通性。如图2所示,首先,参照后续对滑动窗口参数的分析,将窗口长度设置为100 s,窗口滑动步长设置为1个重复时间(repetition time, TR)。然后,在每个时间窗内,通过计算两两脑区之间的皮尔逊相关系数作为脑网络中的节点连边的值,从而得到126个90×90的对称矩阵。同时,为减少弱连接或虚假连接的影响,本研究采用15%的连接密度对每个窗口的连接矩阵进行阈值化。而由于负连接具有模糊的生理解释,在网络阈值之前将其删除。最后,考虑到相邻时间段上同一脑区之间的耦合,将邻接层中同一节点之间的连接权重设置为常用值1[12-13],其余情况的层间连接值为0,从而生成时变多层脑功能网络。

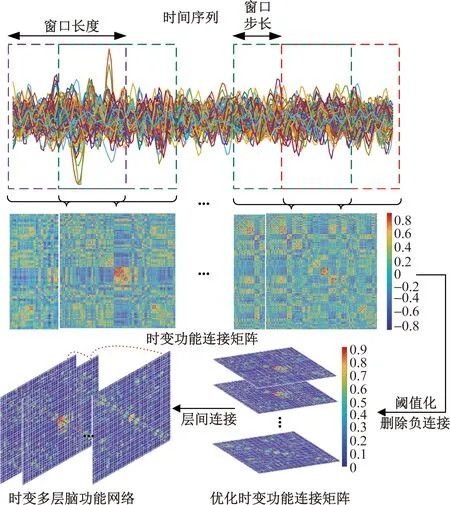
图2 构建多层脑功能网络Fig.2 Construct multilayer brain functional network

1.4 特征提取

利用滑动窗口方法构建时变多层脑功能网络后,选取度、离心率、介数中心度这三个局部拓扑属性作为特征。

1.4.1 单层网络拓扑属性计算

首先,对于每个滑动窗口内的功能连接矩阵,计算度、离心率、介数中心度来刻画单层功能连接网络的拓扑结构。

度是该节点连接到网络中其他节点的边的数量[16]。其计算公式为

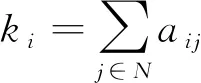
(1)

式(1)中:i、j表示节点;N表示节点数量;aij表示无向加权网络中节点i和节点j的连接。

离心率是该节点到网络中其他节点的所有最短路径中的最大值[22]。其计算公式为

ei=max{d(u,v)}

(2)

式(2)中:d(u,v)指的是节点u到节点v之间最短路径的值。

介数中心度用来衡量节点对于网络的重要程度[11]。其计算公式为

(3)

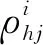
1.4.2 多层网络拓扑属性计算

接着,基于每个单层功能连接网络所得到的拓扑属性,计算时变多层网络的拓扑属性。传统的分析方法中,通过计算所有单层网络的拓扑指标的均值[6]或标准差[14-15]作为多层网络的拓扑指标。但单纯计算均值无法有效利用有代表性的特定属性值的信息[16],而计算标准差的方法又在一定程度上受到均值的影响[17]。为解决以上问题,在已有方法的基础上提出了从极差、相对极差、离散系数这三个视角入手计算多层网络拓扑指标的方法。具体来说,基于极差、相对极差、离散系数视角的方法分别通过计算所有单层网络的拓扑指标的极差、相对极差、离散系数作为多层网络的拓扑指标。其具体的计算公式如表2所示。

表2 多层拓扑属性计算

1.5 特征选择与分类

虽然将多层网络拓扑属性作为特征可以从不同方面描述脑网络特性,但存在冗余或不相关特征影响分类器的性能[9, 23]。因此需要对所计算的特征进行选择,选取组间差异显著的特征进行分类。

本研究把非参数置换检验[10]作为特征选择方法,选取具有显著组间差异的特征。具体来说,针对自闭症患者和健康被试,分别将基于均值、极差、相对极差、标准差、离散系数的多层网络拓扑指标计算方法所产生的270个局部属性进行组间KS非参数置换检验,选取具有显著差异的特征(P<0.05, 已校正)参与分类模型构建。同时将5种方法计算的差异特征首尾串联构建融合特征进行分类。

深度学习已经被广泛应用于各种疾病的诊断中[24-25],但训练其模型需要大量被试[26]。而支持向量机适用于小样本数据集和具有高维的特征[27-28]的脑疾病分类研究。由于本研究最终用于分析的样本量较少,很难获得完全的信息。因此,在对实验被试进行分类的过程中使用支持向量机工具包(https://www.csie.ntu.edu.tw/～cjlin/libsvm/)的径向基核函数(radial basis function, RBF)构建分类模型。

本研究利用留一交叉验证评价分类性能。此外,为了获得更好的分类效果,训练集利用K折交叉验证[29-30]对SVM参数——惩罚因子c和核函数g进行寻优。值得注意的是,构建分类模型前需对分类特征进行标准化。

2 结果

2.1 多层网络拓扑属性分析

为确定基于均值、极差、相对极差、标准差及离散系数计算的多层网络拓扑结构是否存在显著差异,本研究对这5种多层网络拓扑属性计算方法进行了比较,如图3所示。

首先,针对每个被试把通过不同拓扑属性计算方法得到的90个脑区的度、离心率、介数中心度进行平均获得各自拓扑属性计算方法的平均度、平均离心率、平均介数中心度。然后,分别计算自闭症组和健康对照组基于5种拓扑属性计算方法得到的平均度、平均离心率、平均介数中心度的均值,并用直方图进行表示。最后,用色块图表示在自闭症组和健康对照组中分别使用KS检验获得的不同拓扑属性计算方法所得到的平均度、平均离心率、平均介数中心度的统计显著性。结果显示,无论自闭症组还是健康对照组,基于度、离心率及介数中心度分别使用5种统计指标计算的多层网络拓扑属性均存在显著差异(P< 0.05),这表明本研究所提出的方法从不同角度刻画了多层网络的拓扑结构。

2.2 差异性脑区

将基于均值、极差、相对极差、标准差、离散系数计算的多层网络拓扑属性进行组间KS非参数置换检验,选取通过错误发现率校正后P<0.05的脑区作为自闭症组与健康对照的显著差异脑区,其在模板空间中的分布如图4所示,对应的脑区名称及其显著性如表3所示。

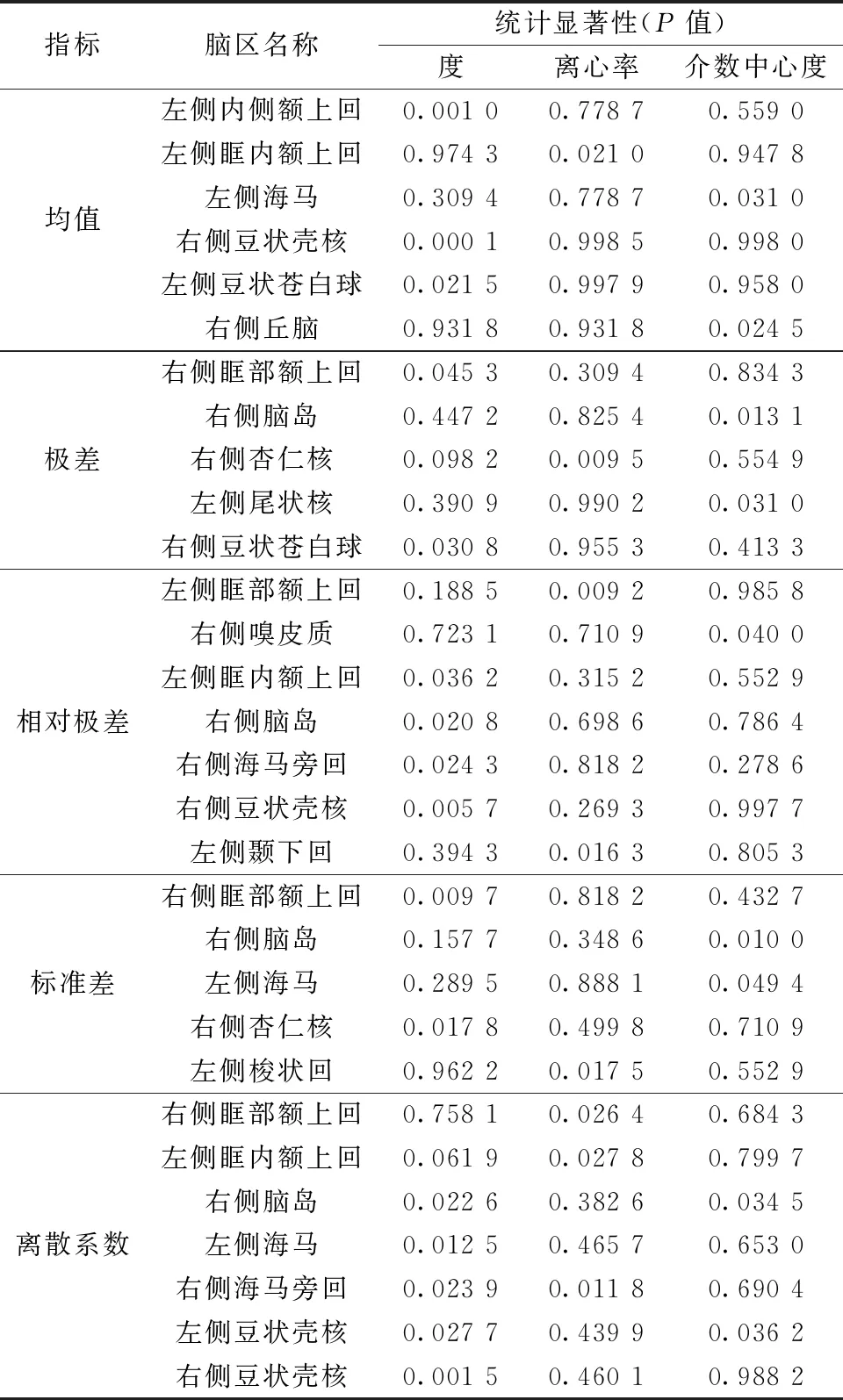
表3 节点指标异常脑区及其显著性

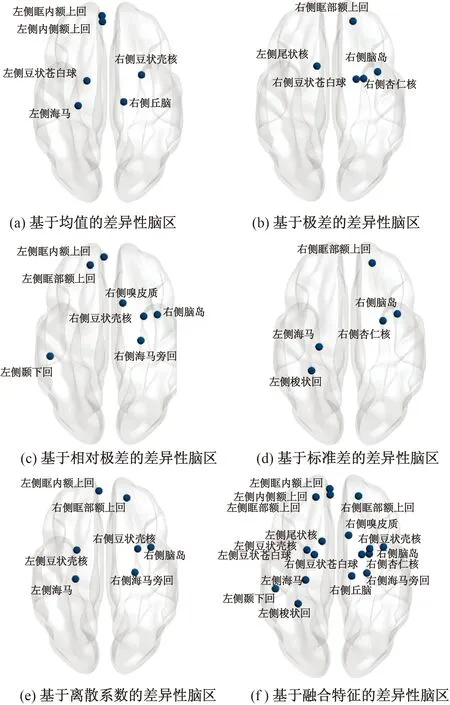
图4 差异性脑区分布图Fig.4 Differential distribution of brain regions

结果显示基于不同视角计算多层网络属性存在较少频繁出现的组间差异脑区,主要包括右侧眶部额上回、左侧眶内额上回、右侧脑岛、左侧海马、右侧豆状壳核。这表明本研究所提出的方法可以从不同角度全面的获得自闭症的差异脑区。同时,这些差异脑区和目前已经被证明与自闭症有关联的脑区一致。Tang等[31]研究定量磁共振成像在儿童自闭症诊断中的应用,结果显示患有自闭症的儿童在双侧豆状壳核、左侧尾状核的脑血流量低于健康对照组。Liang等[32]的研究结果表明,与健康对照组相比,自闭症患者在右侧海马旁回、左侧海马、右侧眶部额上回的功能连接神经回路数量明显减少。Duan等[33]表明自闭症的神经影像学标志物包括右侧嗅皮质、右侧脑岛、左侧颞下回。Qin等[1]的研究发现自闭症儿童相比于健康对照组在额上回脑区的功能连接显著减少。Wang等[4]发现自闭症的发展与脑岛高度相关。Peng等[2]的研究发现,与健康对照组相比,自闭症患者的双侧豆状苍白球在平均度属性上具有显著差异。Yi等[34]的研究显示自闭症患者右侧丘脑的度中心性显著高于健康对照组。Zhao等[35]的研究表明自闭症患者与健康对照组在左侧梭状回灰质体积上存在显著差异。Weerasekera等[36]的研究发现自闭症患者右侧杏仁核的皮层下体积显著高于健康对照组。这表明本研究所提的方法可以有效识别自闭症的生物标志物。

2.3 分类结果

将组间差异显著的脑区特征作为分类器的输入构建分类模型,并从准确率、灵敏度、特异度三个方面对分类器的性能进行评价。

如表4所示,将不同方法的分类结果进行比较。首先,描述了以前传统网络的分类结果。其次,列举了现有研究中将均值或标准差作为多层网络的统计指标计算功能连接从而进行分类的结果。最后,为了消除不同研究所采用的数据和方法的差异,本研究分析了在同一数据集上分别以均值、极差、相对极差、标准差、离散系数为统计指标计算多层网络拓扑属性从而构建的分类器及融合上述所有特征的分类器性能。

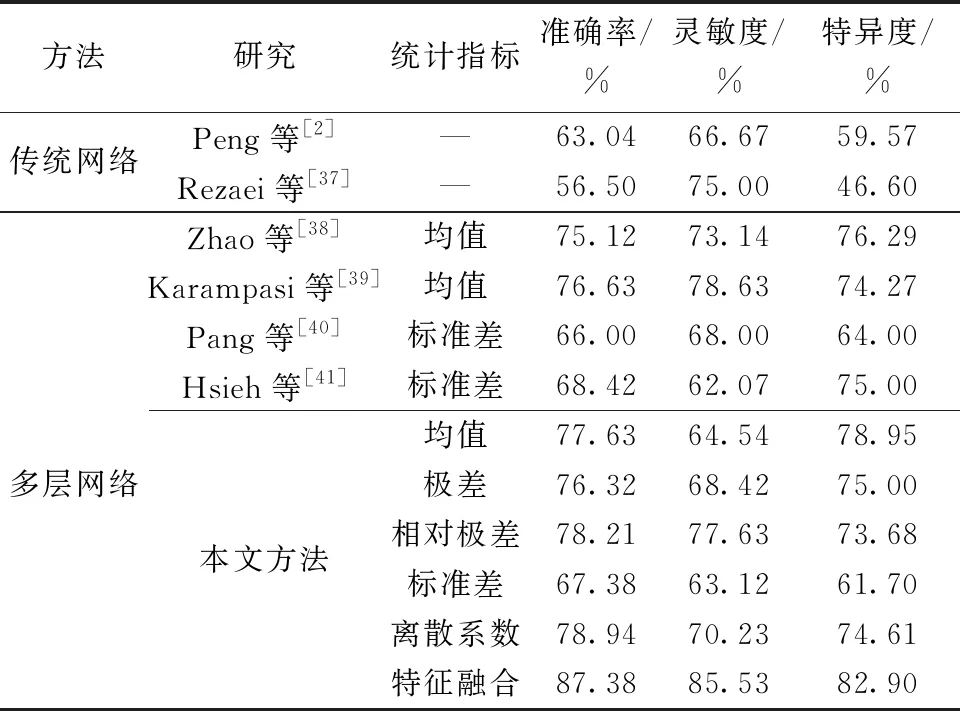
表4 不同方法的分类结果

研究结果显示相比于传统网络,多层网络具有更高的分类准确率,这与多层脑网络包含了大脑的时变信息有关[7]。此外,无论是已有文献,还是本研究所进行的实验,基于相对极差视角的分类准确率均高于基于均值和标准差的分类准确率,这表明相对极差既考虑了各个单层网络属性的整体分布情况,又充分利用了拓扑属性的极值信息。同时,基于离散系数视角的分类准确率高于传统的基于均值和标准差的分类准确率,这表明离散系数在考量所有单层网络拓扑属性的标准差的基础上避免了均值的影响。值得注意的是,基于极差视角的分类准确率高于基于标准差视角的分类准确率,略低于Karampasi等[39]的研究和本研究中基于均值视角的分类准确率。这可能由于基于极差的视角只应用了多个单层网络中拓扑属性的最大值和最小值,包含较少的信息。但是基于相对极差视角的方法应用了极差信息,而且分类效果较为理想。因此,这表明拓扑属性中的极值信息在一定程度上有利于自闭症的分类。此外,结果显示基于多特征融合的分类效果最好,分类准确率为87.38%,灵敏度为85.53%,特异度为82.90%。这表明融合特征方法可以弥补从单一角度考虑多层网络拓扑结构时缺失的信息,从而包含更多的自闭症生物学标志物,因此可以有效提高疾病的分类表现。

由此可见,使用本研究所提出的方法可以更好地实现对自闭症患者的分类,这为自闭症的临床诊断提供了一种新的思路。

2.4 特征权重

此外,使用ReliefF算法[42]分析基于均值、极差、相对极差、标准差、离散系数计算多层网络属性及融合所有特征对分类结果的贡献程度。该算法依据每种类别和功能的相关性分配不同权重,分类能力越强的特征对应越大的权重。利用直方图表示不同分类方法的权重值,并使用色块图表示各自方法分类权重之间的统计显著性。如图5所示,不同方法的分类权重存在差异。同时,与分类结果一致,基于融合特征方法的分类权重显著高于(P<0.05)任意基于单一视角的分类权重。这表明融合特征弥补了单一统计指标缺失的信息,从多个角度综合捕捉多层脑网络的拓扑特征,进而更好地识别自闭症。

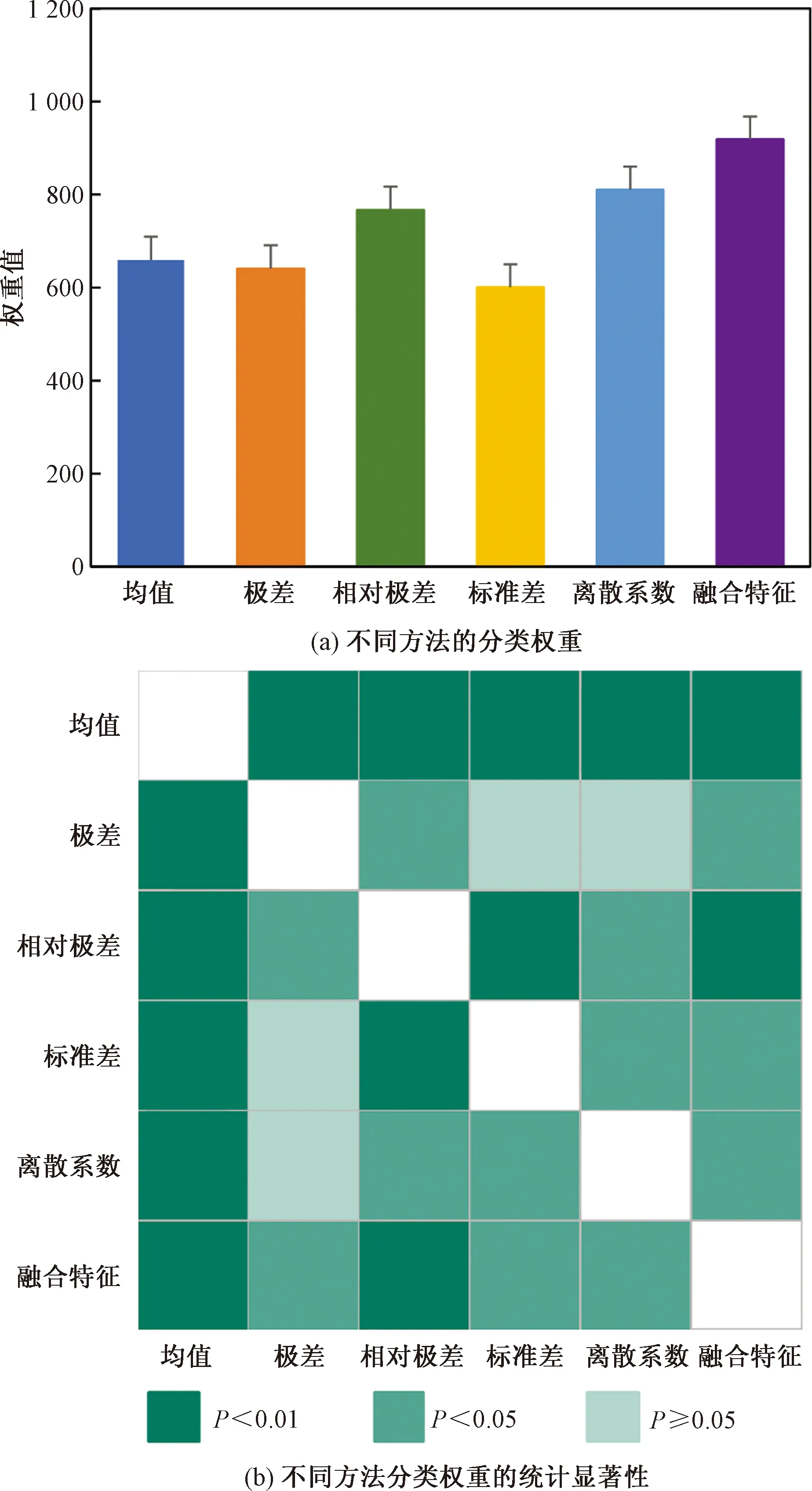
图5 不同方法的特征权重Fig.5 Feature weights of different methods

2.5 可重复性验证

为了验证基于统计指标的多视角多层脑网络拓扑属性计算方法的可重复性,从ADNI数据集中选择29例阿尔茨海默症患者和30例健康被试,分别基于均值、极差、相对极差、标准差、离散系数视角计算多层网络拓扑属性,通过组间差异显著的脑区特征实现分类,并对比不同多层网络拓扑属性计算方法及融合所有特征的方法的分类性能,具体效果如表5所示。

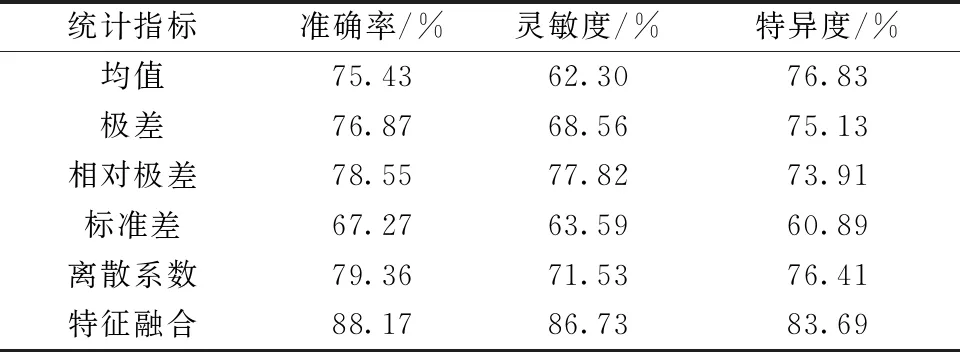
表5 ADNI数据集下不同方法的分类结果

结果显示基于极差、相对极差、离散系数视角的分类准确率高于基于均值和标准差视角的分类准确率,同时,多视角融合特征具有最好的分类效果。这表明,本研究所提出的方法在不同的数据集下具有可扩展性,可以更有效的诊断疾病。

3 方法论

鉴于目前针对多层网络拓扑指标的计算存在泛化性差、考量角度单一的缺点,本研究在现有的基于均值、标准差计算多层网络拓扑属性的基础上提出了基于极差、相对极差、离散系数计算多层网络拓扑属性的方法,同时融合所有特征进行分析,从而表征大脑的时变特性,寻找组间差异特征实现对疾病的分类。虽然最终结果被证明与数据集无关,但仍会受到一些重要参数的影响,因此,本研究分析了在自闭症数据集的实验中涉及的参数(如滑动窗口长度、滑动窗口步长、支持向量机分类模型参数c和g)的选择对分类准确率的影响。

3.1 滑动窗口长度

滑动窗口长度的大小会影响整体时间窗的数量和单层网络的构建,从而最终影响多层脑网络的构建。因此,在针对自闭症数据集的实验中,固定其他参数,研究滑动窗口长度分别为70、80、90、100、110、120 s时疾病的分类结果。如图6所示,当滑动窗口长度为100 s时基于均值、极差、相对极差、标准差、离散系数及特征融合视角的方法均获得最高的分类准确率。这表明过小的滑动窗口长度可能导致相似的时间序列被划分到不同的窗口,从而包含很多冗余特征,造成分类结果较差。而滑动窗口长度过大使得时间窗数量较少,进而导致时变特性不明显,因此最终的分类准确率较低。

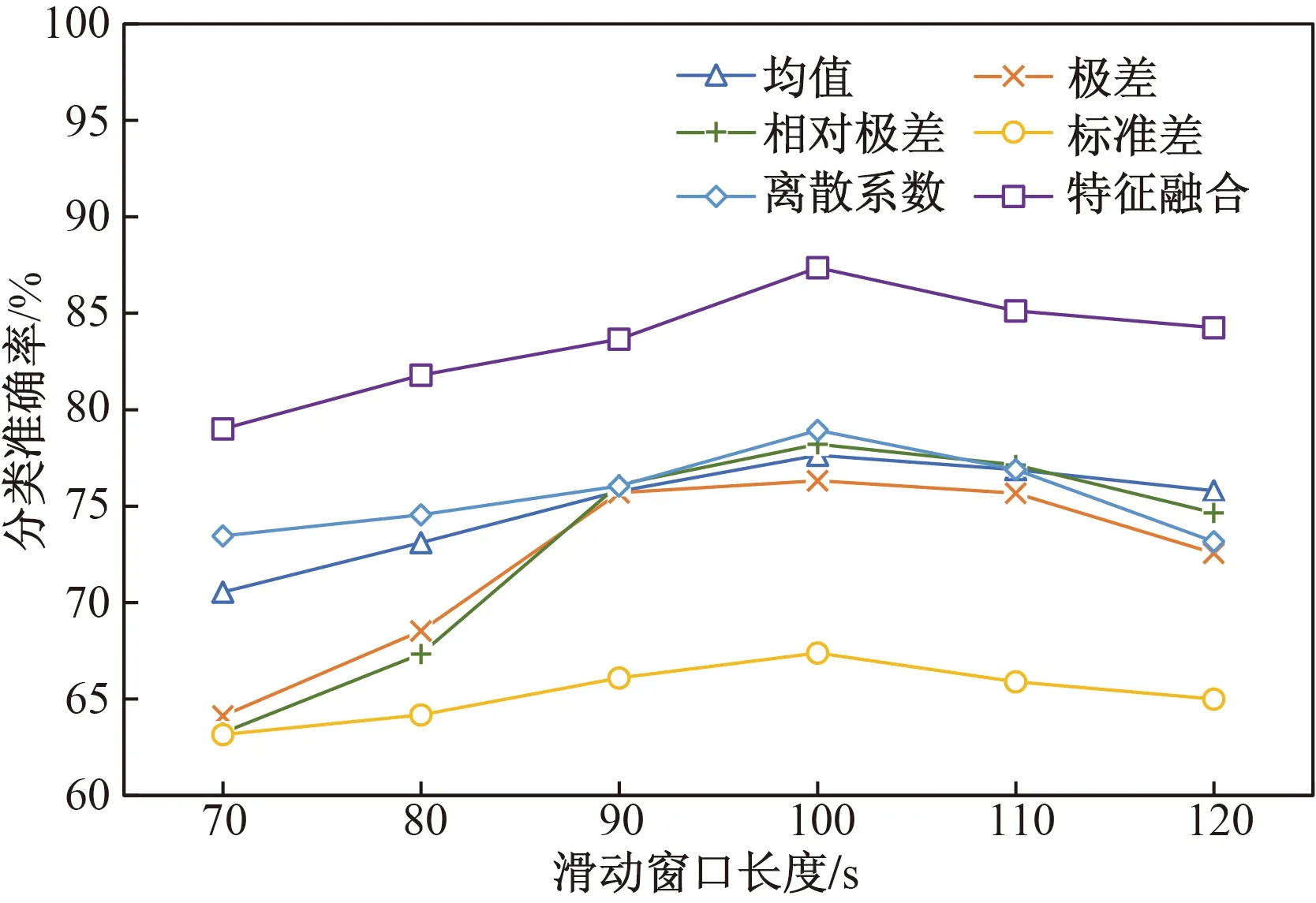
图6 不同滑动窗口长度的分类结果Fig.6 Classification results of different sliding window lengths

3.2 滑动窗口步长

除滑动窗口长度外,滑动窗口步长也会影响多层脑功能网络的构建。因此,如图7所示,在固定其他参数的基础上,研究滑动窗口步长分别为1、2、3、4、5、6 TR时自闭症的分类结果。

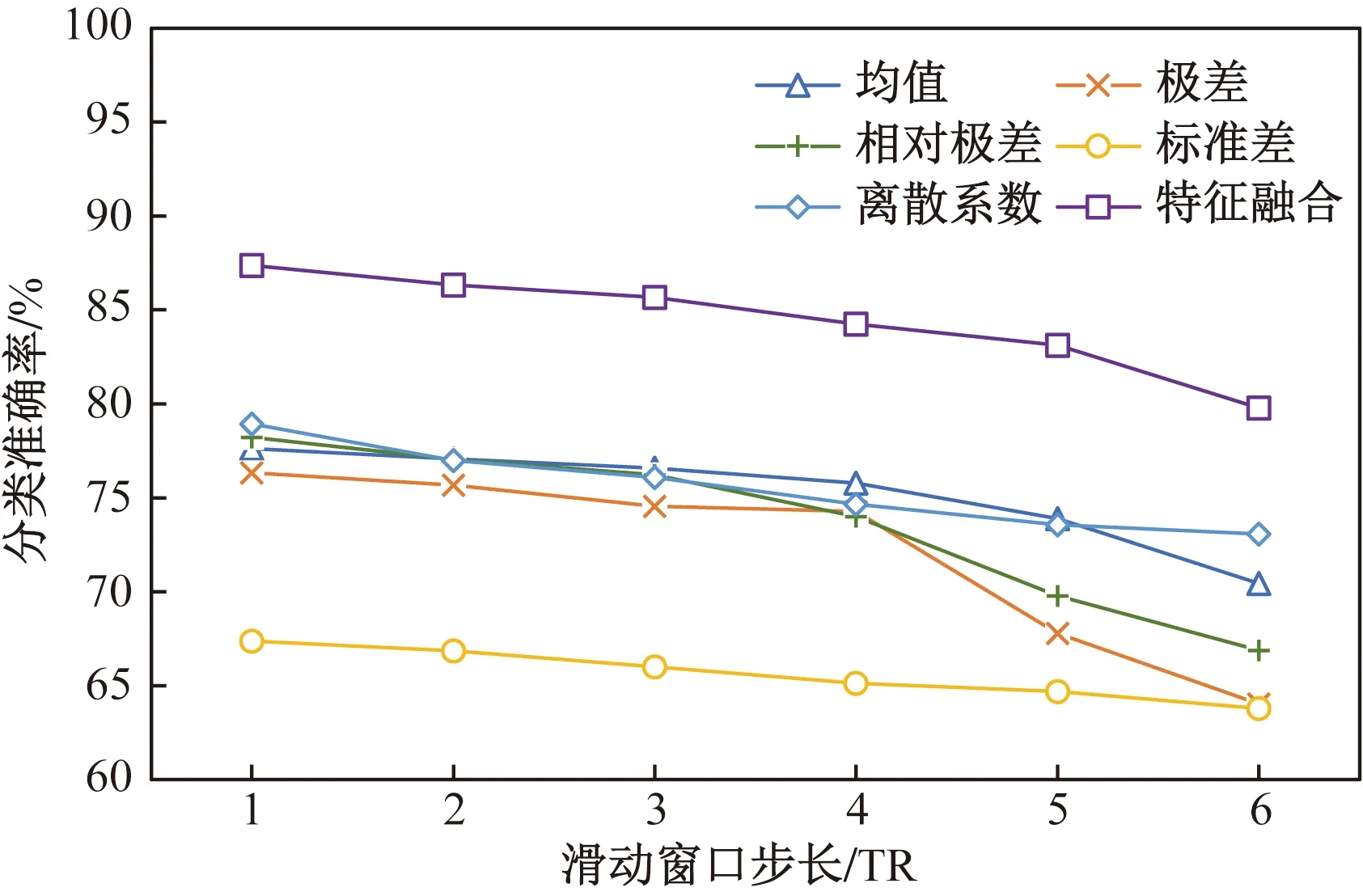
图7 不同滑动窗口步长的分类结果Fig.7 Classification results of different sliding window steps

结果显示,当滑动窗口步长为1 TR时基于均值、极差、相对极差、标准差、离散系数及特征融合视角的方法均获得最高的分类准确率。同时分类准确率随着滑动窗口步长的增大而降低。这表明滑动窗口步长越大,划分的时间窗数量越少,导致可能没有充分体现脑网络的时变特性,进而分类效果较差。

3.3 SVM分类模型参数的影响

SVM分类模型适用于具有高维特征和小样本特性的数据集,被广泛应用于脑疾病研究中。而RBF核函数不受样本数量的影响且可以解决线性不可分问题。因此,使用RBF核函数构建分类模型。

在SVM模型中惩罚因子c和核参数g的不同取值会导致不同的分类结果。c表示对误差的容忍度,其值过大或过小均会导致泛化能力变差;g隐含的决定原始特征数据映射到高维特征空间的分布情况,从而影响训练和预测的速度。因此,c和g的合理组合对分类器模型的构建至关重要。

本研究在针对自闭症数据集的实验中,设置参数c和g的范围为[2-8, 28],步长为1,采用网格搜索方法选取最优的c、g组合构建分类模型。具体来说,将训练集当作原始数据集,针对每一组给定的c和g的值,使用K折交叉验证计算分类准确率,选取最高分类准确率对应的c和g的值作为最佳参数组合。由于基于融合特征方法的分类效果最好,本研究展示了此方法下c和g的参数寻优结果。如图8所示,当c的值为1,g的值为0.25时得到最好的训练集验证分类效果,其准确率为92.135%。

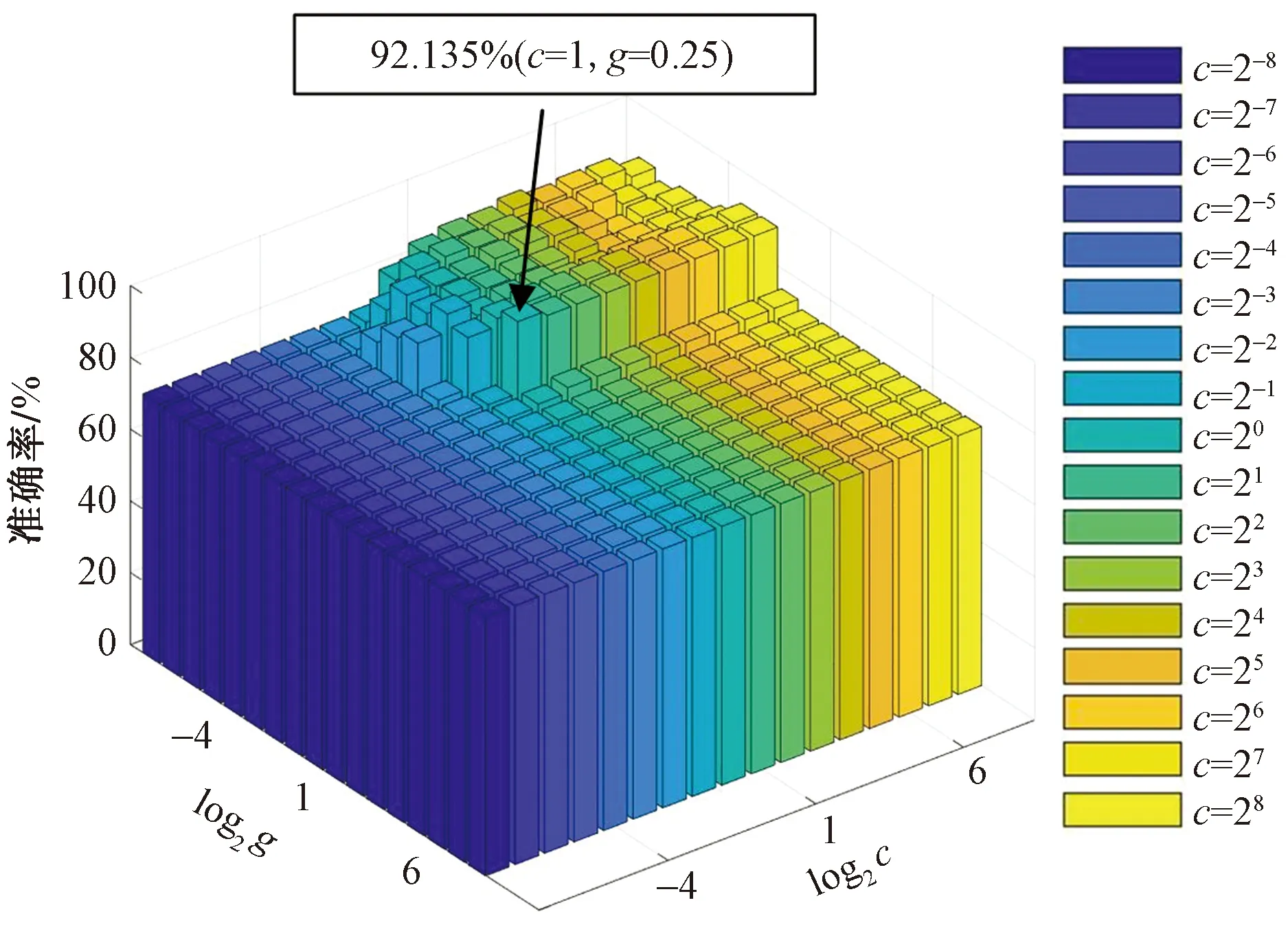
图8 c和g的参数寻优结果Fig.8 Parameter optimization results of c and g

4 结论

本研究考虑了大脑跨脑区交互作用的时间变化,利用滑动窗口技术构建多层脑功能网络来表征时变特性。鉴于已有的研究中针对多层网络拓扑指标的计算方法泛化能力差、考量角度不全面的现状,在基于均值和标准差计算多层网络拓扑属性的基础上,提出了基于极差、相对极差、离散系数表征多层网络拓扑特征,研究异常拓扑属性并实现分类。

结果显示,无论是ABIDE数据集还是ADNI数据集,基于相对极差、离散系数视角的分类准确率均显著高于传统基于均值和标准差的分类准确率,这表明本研究提出的方法可以更好地识别疾病且具有可扩展性。同时基于融合特征的分类性能优于任意单一视角下的分类性能。因此,从多个角度表征多层网络的拓扑结构具有较好的疾病诊断效果。

但本研究仍存在局限性。首先,鉴于数据量较少实验采用传统统计分析方法选择特征并使用机器学习实现分类,将来纳入更多样本后可以使用深度学习方法进行分类。其次,本研究使用度、离心率、介数中心度三个局部属性进行分析,忽略了整体角度对多层网络拓扑结构的影响,将来可以结合全局指标进行实验。最后,静态功能连接网络和动态多层功能连接网络为大脑交互提供互补信息,将来可以把两者结合起来,研究其对疾病诊断的贡献。