直流电晕放电特性分析

2023-07-26邹岸新王守刚杨滔刘岩李永明

科学技术与工程 2023年19期

邹岸新, 王守刚, 杨滔, 刘岩, 李永明

(1.国网重庆市电力公司超高压分公司, 重庆 400039;2.输配电装备及系统安全与新技术国家重点实验室(重庆大学), 重庆 400044)

高压直流输电技术是中国重点发展方向之一,能够将作为社会经济发展重要支撑的电力资源进行优化配置。随着电压等级不断提高,输送容量不断扩大,使得特高压直流输电技术不断发展[1-2]。但当高压直流输电线路的电压加到一定等级并且超过空气的击穿强度时,将会使空气中的气体电离,会使导线表面发生电晕放电现象[3-4]。电晕放电产生的电荷受空间电场的影响做漂移扩散的运动,最终产生的附加场会直接影响空间电场的分布[5]。并且电荷在空间中与运动还会产生电晕电流[5-6],直接决定了由电晕放电引起的电晕损耗,并且在放电过程中产生的声干扰、无线电干扰、绝缘劣化等电磁环境污染问题以及电晕放电造成的腐蚀设备表面和缩短设备使用寿命问题日渐受到重视[7-9],因此开展电晕放电围观物理过程研究对于探究电晕放电的特征规律、指导输电线路离子流场计算具有重要理论价值。

对于电晕放电的放电机理以及形成的离子流的相关特性,国内外学者建立不同的理论模型并进行大量的理论试验研究,分析放电机理以及电晕放电后产生的各种电磁影响。文献[10]提出一种考虑导线表面电场不均匀性对电晕放电影响的方法,研究超高压交流输电线路电晕放电对地面电场的影响。文献[11]通过悬空导线电位补偿法进行测量电晕放电产生的空间电荷的单位分布。文献[12]建立基于泊松方程和流体动力学方程的负电晕放电仿真模型,定量研究负电晕放电中的微观物理过程,并研究不同位置的颗粒物的运动特性。文献[13]建立Navier-Stokes方程耦合的二维单极离子漂移模型,研究导线电晕放电时电压和导线直径对离子风场分布和流速大小的影响。Javandel等[14]建立漂移扩散模型来模拟正负电压下的电晕放电差异性。 Font等[15]使用室内电晕笼和各种导体配置对高压直流输电线路的直流电晕特性进行了实验和模拟研究,以指导土耳其拟建高压直流输电线路的设计。Fahmi等[16]采用3种漂移扩散模型和泊松方程,用有限元方法求解了负电晕放电现象,研究带电物质的空间分布、电场分布和电离率。

电晕放电微观过程中会产生大量的激发态粒子、带电粒子等,空间难度大,特别是对于分子气体放电,动理学规律极其复杂。由于缺乏有效的等离子体诊断手段,电晕放电的很多微观参数通过试验获取还是有一定难度,并且应用数值计算方法分析效率不高。电晕放电属于非平衡放电中低温等离子体范畴,其微观物理过程是一个典型的多物理场耦合过程。

为此,建立完全自洽的等离子体模型和简化的电晕放电模型,研究考虑±30 kV的直流电晕放电情况。结合域方程的推导,描述载流子在传输区域中的传输,计算电晕放电产生的空间电荷密度和电势。

1 等离子体模型

1.1 等离子体建模

等离子体通常被称为物质的第四态,即带电粒子、中性粒子和电磁场的导电性组合体,呈现出高度激发的不稳定态。建立等离子体仿真模型,如图1所示,求解漂移扩散近似电子和离子连续性及动量方程,与泊松方程自洽耦合。

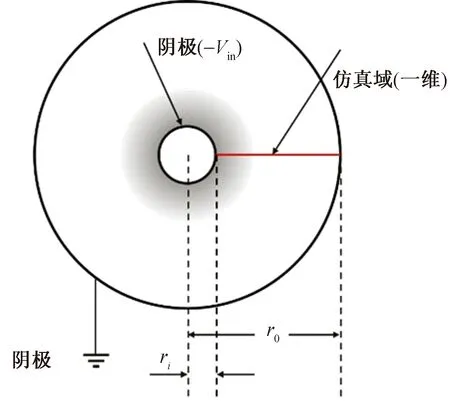
图1 同轴构型的非等比例横截面Fig.1 Non-equivalent cross-section of the coaxial configuration

图1显示了以负极为例的仿真模型几何结构的横截面,内部电极半径ri为100 μm,电极之间的间隙r0-ri为10 cm,阴影区域表示由阴极附近产生的正空间电荷分布产生的电离区域。假设观点在径向上均匀扩散,所以可以简化为在电极之间的径向方向上是以为的。假设其体温度和空气数密度是恒定的。其中采用“局部场近似”,这意味着假设传递系数和源系数通过约化电场 (E/N) 进行适当的参数化。并且也不涉及求解平均电子能的流体方程,因此,数值问题求解的复杂性可以大幅度降低,提高计算效率。

“局部场近似”有效的条件是,电子从电场中获得能量的速率与能量损耗率局部平衡。当满足这一条件时,电子平均属性可以表示为约化电场的函数[17],此时电子与电场是处于局部平衡状态的。

使用图1所示的模型模拟在内导体上施加电势时惰性气体的电离以及带电颗粒的传输。高电势和较小的导体曲率半径共同产生的强电场会导致电晕丝周围的惰性气体电离。

1.2 域方程

先求解电子密度的漂移扩散方程来计算电子密度,避免因为使用电晕放电接口的强近似而只求解离子传输问题。求解公式为

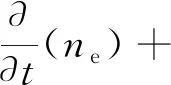
(1)

式(1)中:ne为电子密度;μe为电子迁移率;E为电场强度;De为电子扩散系数;Re为离子复合项。

应用“局部场近似”时,传输系数和源系数直接通过约化电场来直接映射,电子密度方程不再求解。实际上,当使用局部场近似或局部能量近似时,传输系数和源系数仍以平均电子能的函数形式给出[18]。但使用“局部场近似”时有所不同,此时必须提供一个能将平均电子能与约化电场联系起来的函数,而使用“局部能量近似”则不需要。平均电子能的计算公式为

ε=F(E/N)

(2)

式(2)中:N为气体粒子数密度。

根据电子迁移率计算出电子扩散系数,表达式为

De=μeTe

(3)

式(3)中:Te为电子温度。

等离子体化学成分的速率系数决定了源系数。对于速率系数的求解,电子源项表达式为

(4)

式(4)中:xj为反应j的目标物质的摩尔分数;kj为反应j的速率系数,m3/s;Nn为总中性数密度,m-3。

对于直流放电,使用汤森系数而不是速率系数来定义反应速率。此时,电子源计算式为

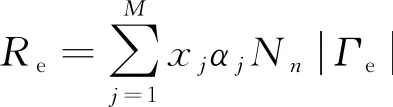
(5)

式(5)中:αj为反应j的汤森系数,m2;Γe为电子通量,m2/s。当电子通量像直流放电一样被场驱动时,汤森系数可以提高数值方案的稳定性[19-20]。

对于非电子物质,对每种物质的质量分数求解以下方程,即

(6)

式(6)中:ρ为混合物的密度,kg/m3;wk为第k种物质的质量分数;u为质量平均流体速度矢量,m/s;jk为扩散通量矢量;Rk为第k种物质的速率表达式,kg/(m3·s)。

静电场的计算方程为

-∇·ε0εr∇V=ρ

(7)

式(7)中:ε0为真空介电常数;εr为相对介电常数;V为电势,空间电荷密度ρ根据模型中指定的等离子体化学成分自动计算,公式为

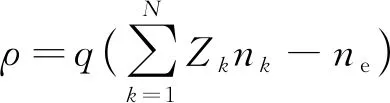
(8)

式(8)中:Zk为第k种物质的电荷量;nk为第k种物质的密度。

2 简化的电晕模型

用等离子体自洽模型需要非常小的时步来描述其物理场,对于电晕放电进行建模的计算量非常大。原因之一是可能会发展出电离波,增加了问题的数值难度,并增加了计算时间。高维模型对工业应用而言不太现实,因此采用简化模型。

简化模型使用与图1所示的等离子体模型相同的几何结构,满足基于带电载流子传输的电流守恒,由于需要在电晕电极上同时给出电势和电场,因此模型不是自洽的,即维持放电所需的电场不是根据第一原理获得的,电子和离子传输、电子从电场中获取能量,电子在于背景气体碰撞时损失能量。

在稳态下的电晕放电中,背景气体的电离发生在离电晕电极非常近的区域,即所谓的电离区。在电离区和大电极 (通常接地)之间,只有一种载流子:正离子或负离子,具体取决于电晕的极性。该区域称为传输区域。对于某些涉及电晕放电的应用,不需要用到等离子体模型的所有复杂方面,可以使用简化的模型来获得空间电荷密度和电势。

使用简化的模型来描述一种载流子在传输区域中的传输。维持放电的等离子体物理场浓缩在电晕电极的给定电场区域。显然,电晕电极上提供的电场的大小对于获得电势和空间电荷密度的精确值是至关重要的。

2.1 域方程

根据电荷守恒方程和泊松方程,建立简化的电晕模型,以此来求解载流子在电晕放电过程中的传输问题。当仅包括电场漂移时,域方程为

∇·J=S

(9)

J=zμρE

(10)

ε0∇2V=-ρ

(11)

式中:J为电流密度,A/m2;S为电流源,A/m3;z为电荷数;μ为迁移率,m2/(V·s);ρ为空间电荷密度,C/m3;E为电场;V为电势;ε0为真空介电常数,获得输运方程,即

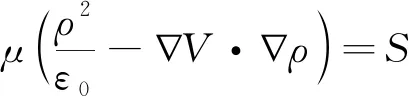
(12)

假设迁移率是恒定的。在没有源项的情况下,该方程广泛应用于模拟静电除尘器中的空间电荷密度的假设格式,即

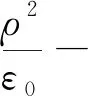
(13)

在简化形式下,方程不依赖于载流子的任何属性,正负电晕中V和ρ的解是对称的。与等离子体产生分布和维持放电相关的信息,都体现在内电极的边界条件设置里,在这里求解的域方程中没有涉及。

2.2 边界条件

电晕电极上电场的法向分量用作泊松方程的边界条件,表达式为

n·E=E0

(14)

泊松方程的另一个边界条件是外电极处的V=0。边界条件涉及采用拉格朗日乘子[21]求得电晕电极上的空间电荷密度ρq,从而验证施加的电势V0。表达式为

V-V0=0

(15)

在简化模型中,设置在电晕电极上施加电势和电场。为了获得和等离子体模型一致的预测的物理结果,应用匹克定律求解起始电晕电场,保证导线处的场强严格接近真实的数值。匹克定律为

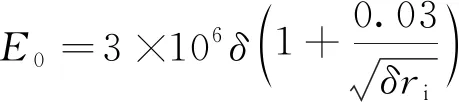
(16)

式(16)中:E0为击穿电场,V/m;δ为气体数密度;ri为电晕电极的半径。

3 仿真结果

3.1 负电晕放电微观过程

根据图1建立的模型,负电位(-Vin)施加在内部导体(阴极)上,外电极接地(阳极),分析负极导线周围的空间电荷分布情况。呈现和讨论的所有结果都对应于稳态操作。在内电极上施加-30 kV时的直流负电晕,获得负电晕的带电物质数密度如图2所示(为更清晰地展示粒子密度在截面上的分布情况,将计算结果取对数进行数学处理)。

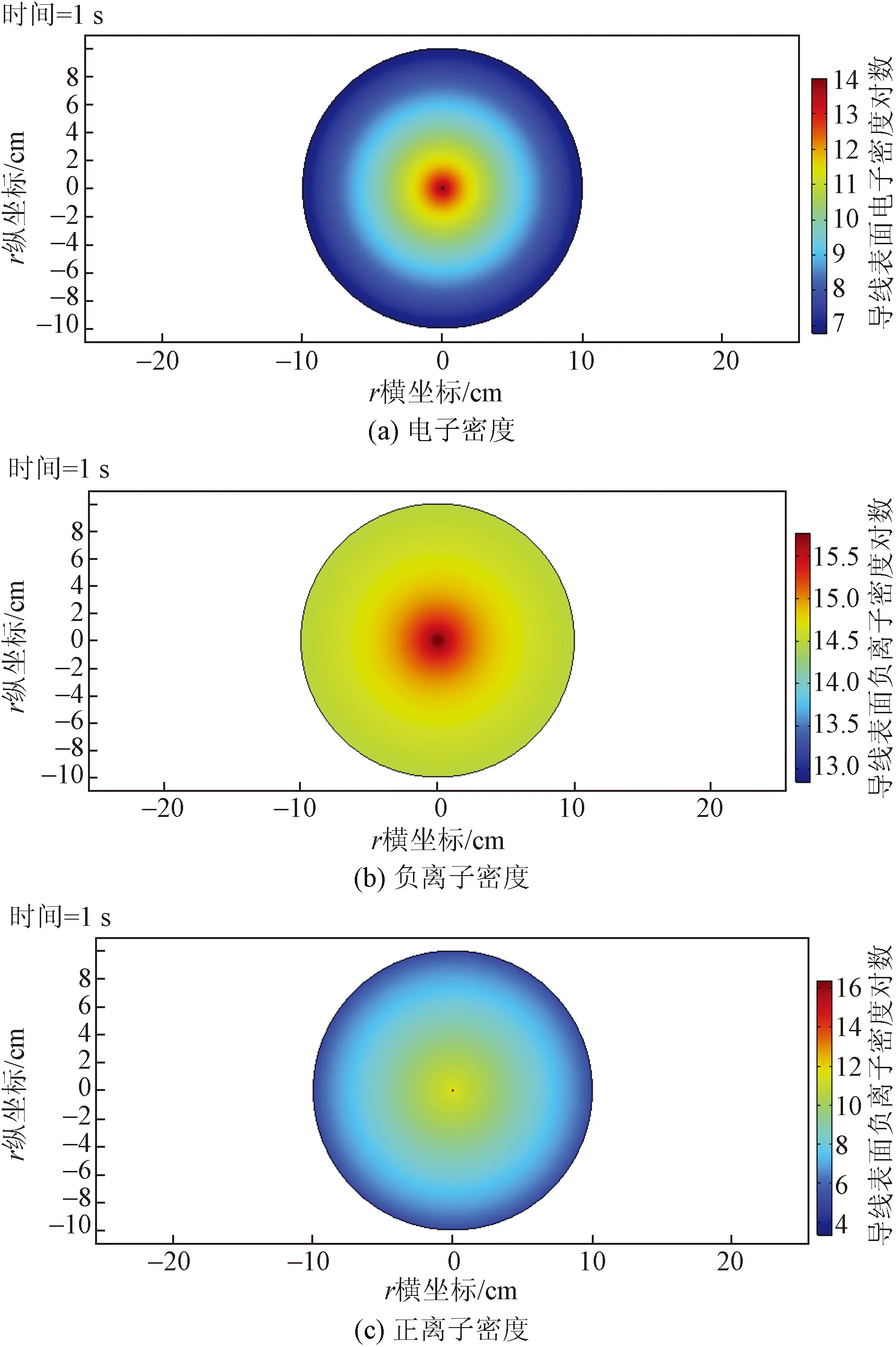
图2 负电晕带电物质数密度的二维表示Fig.2 Two-dimensional representation of number density of charged matter in neqative corona

图2是带电物质数密度通过一维解获得的二维表示。在电晕放电中涉及各种各样的电离反应,其中最主要的是电子和空气中中性分子碰撞电离。为了深入探求电晕放电的微观机理,需要对电子密度的分布进行分析计算,因为在外加电场和重粒子之间,电子是能量传递的主要载体。电子在向阳极运动的过程中,会不断和空气中的物质发生碰撞和电离,朝向阳极的基本电子崩也随之建立,同时激励反应和电离反应也在伴随产生。因此从阴极到阳极,电子的分布区域逐渐扩充,这一点从图2中可以明显看出。电极的大部分体积被在阳极方向上漂移的负离子填充。

图3～图5显示了电子温度、电势和约化电场的结果。可以看出,在到达电极的部分区域具有弱电场,因而具有电子温度。在该区域中,电子没有足够的能量发生电离并有效的附着形成负离子。因此,放电的一个较长的空间部分向接地电极漂移的负离子控制。另外,在此区域中,电荷分离几乎不会使外加电势的分布发生形变。

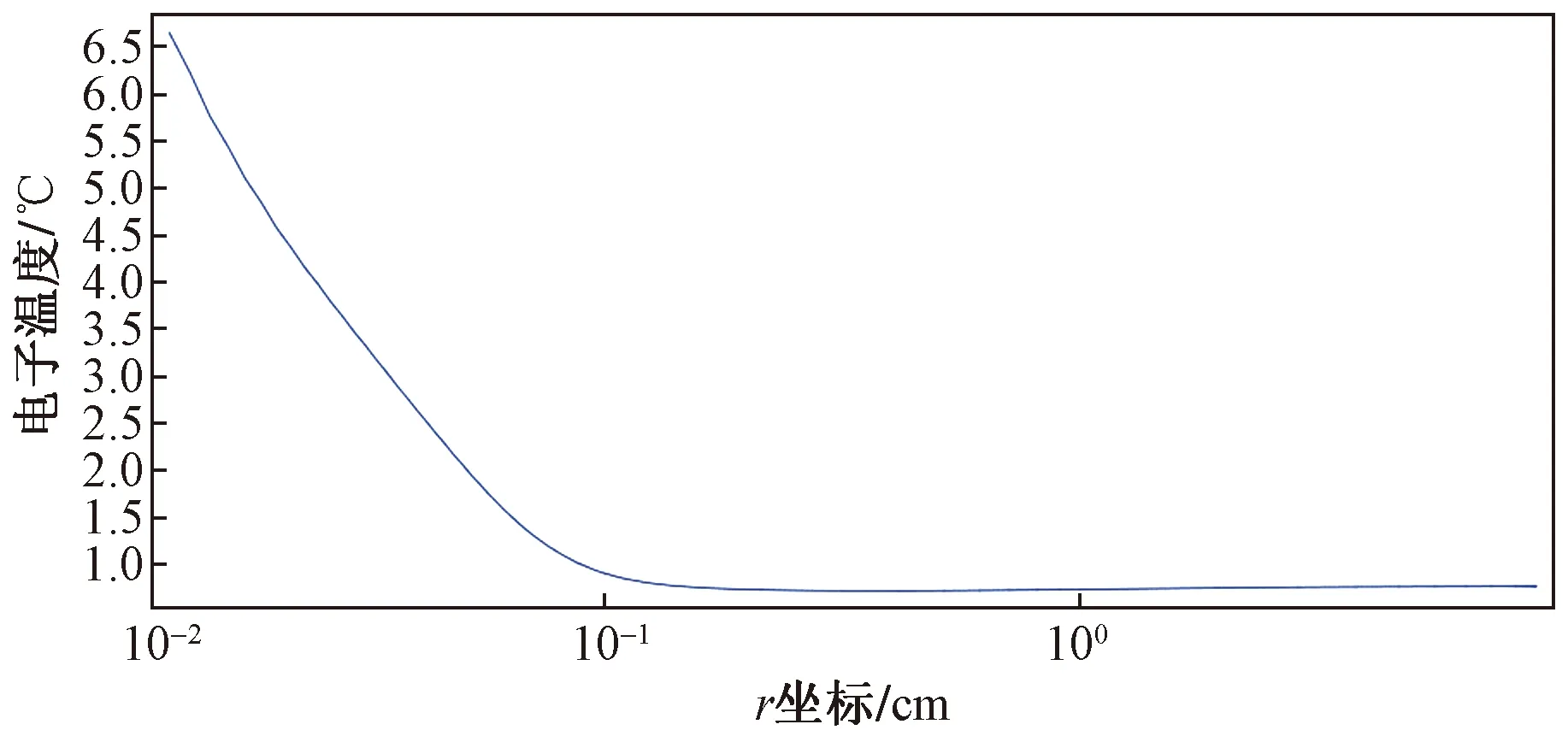
图3 电子温度的空间分布Fig.3 Spatial distribution of electron temperature

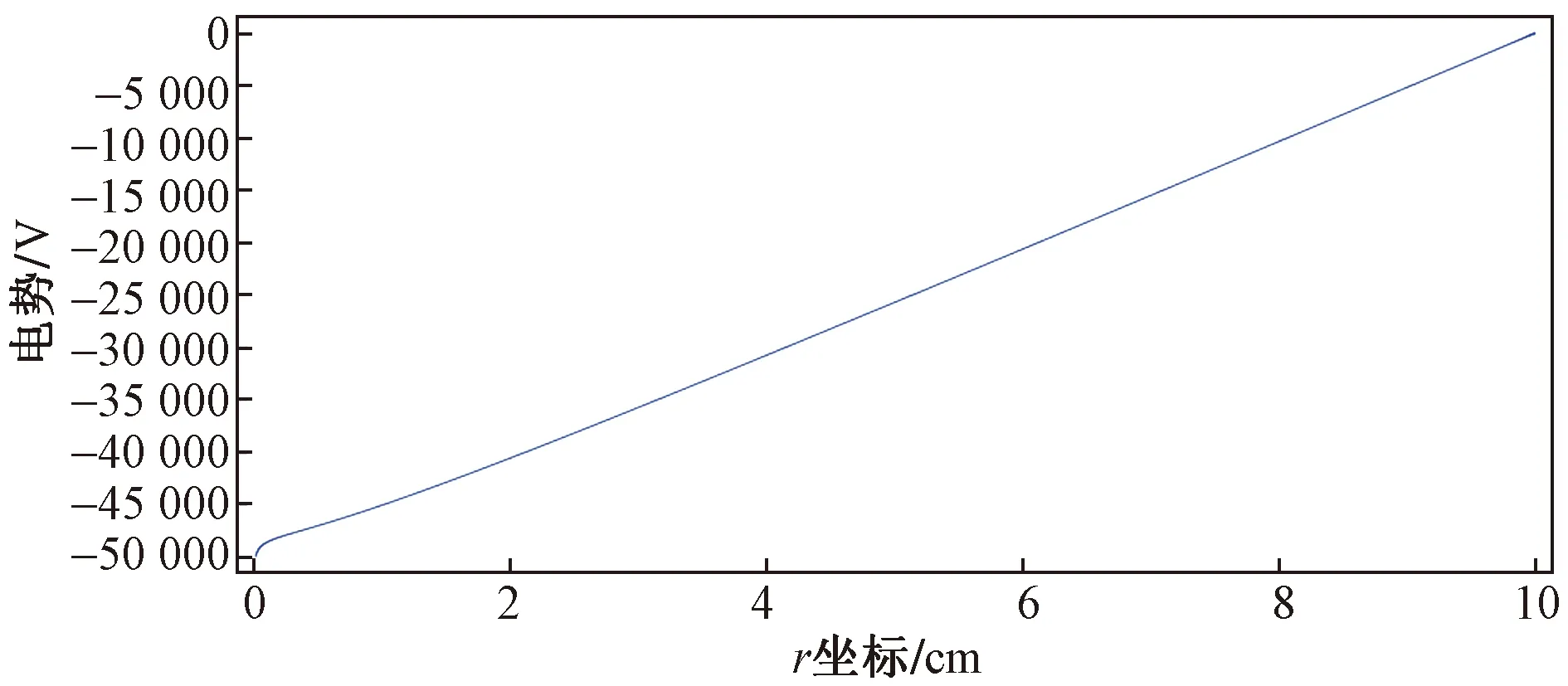
图4 电势的空间分布Fig.4 Spatial distribution of electric potential

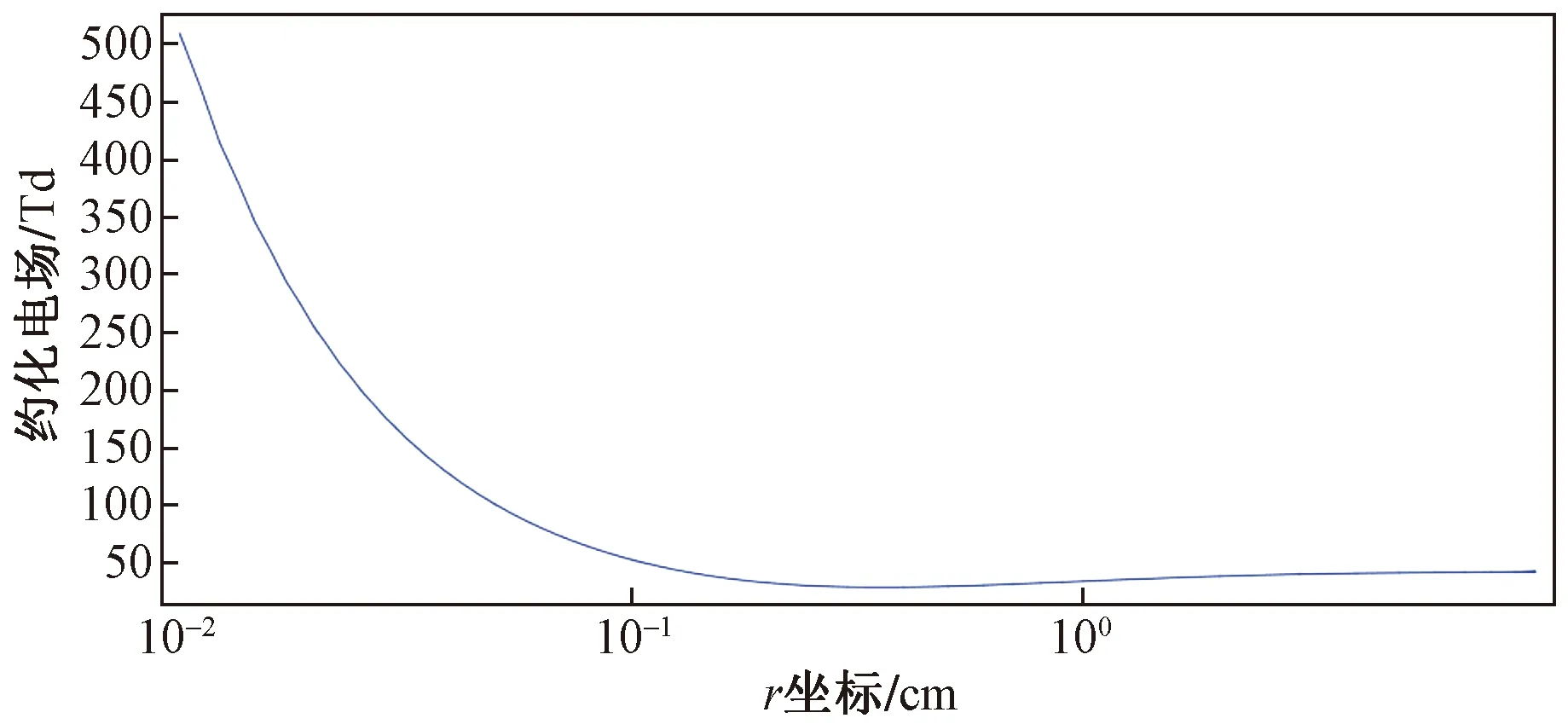
图5 约化电场的空间分布Fig.5 Spatial distribution of thereduced electric fields

图6显示了接地电极出总离子流的绝对值与内电极处外加电压的绝对值的函数关系。电流-电压特性遵循预期的二次定律。所获得的电流密度值也与这种放电的值一致。

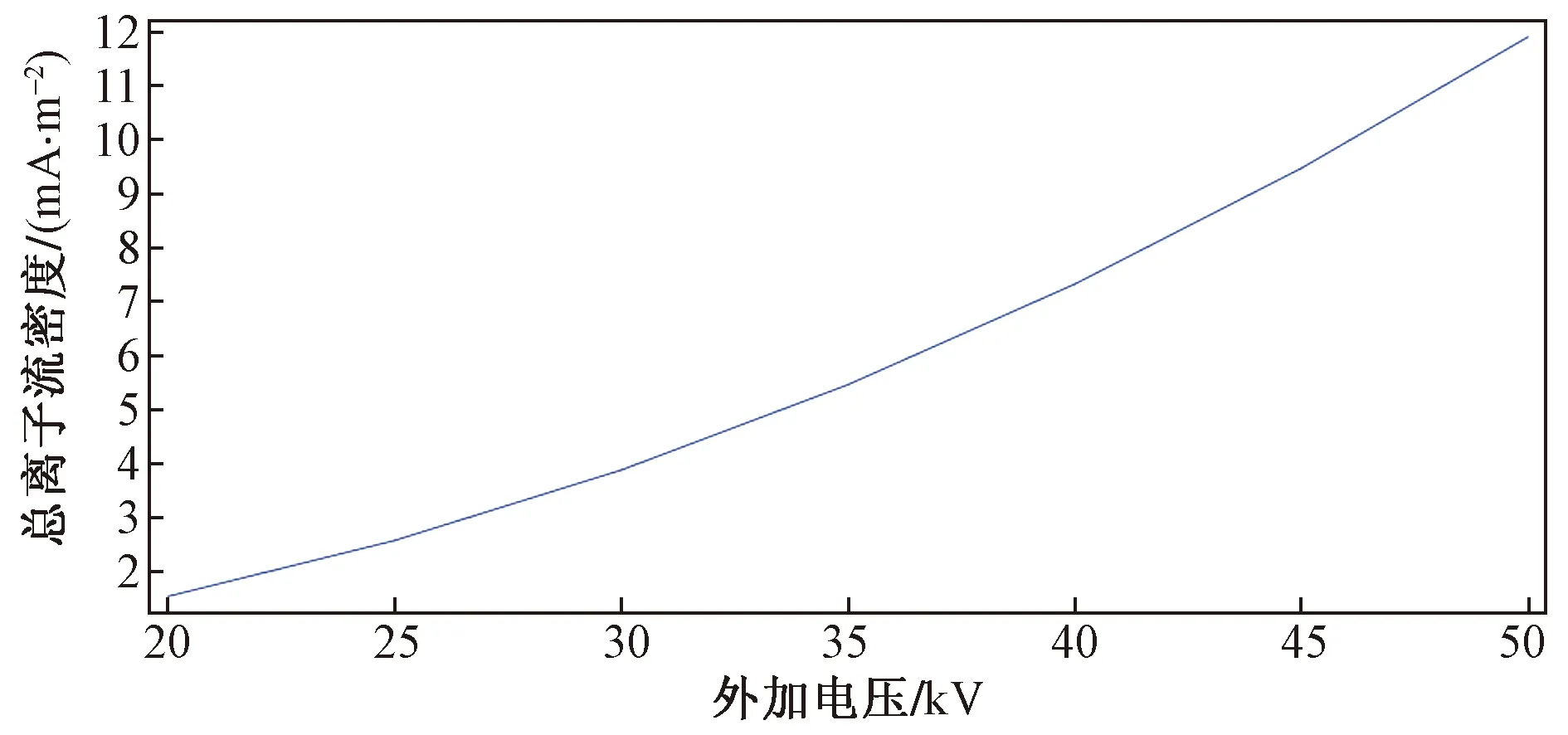
图6 接地电极总离子流密度与外加电压的函数关系Fig.6 Function of total ion current density of grounded electrode and applied voltage

3.2 自洽的等离子体模型

空气中等离子体的化学性质非常复杂,对主要激发态的详细研究很容易产生数百种反应。但在研究过程中主要关注的是电荷粒子密度的分布以及产生的电流情况。因此,在建模中可以使用一组简化的反应来替代,描述干空气背景下带电物质的产生和消失。具体计算结果如图7所示。

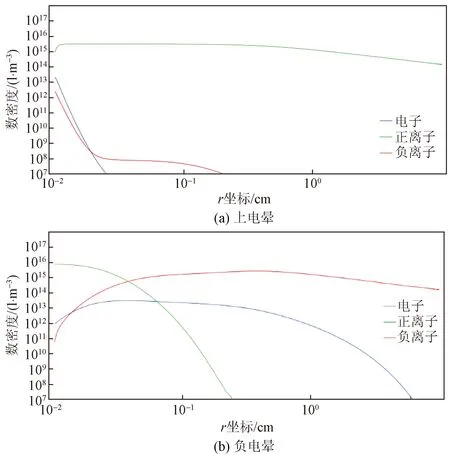
图7 电晕带电物质的数密度Fig.7 The number density of charged matter in corona

图7显示了用等离子体模型获得的正负电晕的带电物质的空间分布。从中可以看出,电晕放电在两个区域中进行:一个是主要发生电离区,另一个是粒子传输区。电离区主要是发生在阴极附近1 mm以内的区域,传输区是到达接地电极的其余部分。两个区域中关于粒子的分布有明显不同。图7(a)表示的正电晕带电物质浓度分布中,正离子密度在所有区域中占主导地位,而在图7(b)关于负电晕的描述中,正离子仅在阴极下降区占主导地位,而在传输区中,负离子占主导地位。

图8描述了通过自洽模型获得的各种极性的主要载流子的速率表达式:正离子用于正电晕,负离子用于负电晕。正电晕中,正离子是在电晕电极附近的狭窄区域中由基态的电子碰撞电离产生的。负电晕中,负离子是通过电离和传输区域中的电子附着产生的。

图8 正电晕的正离子和负电晕的负离子速率表达式Fig.8 Expressions for the rates of positive ions and negative ions of positive corona

3.3 简化模型与自洽的等离子体模型对比

空间电荷密度的分布是整个放电过程中带点粒子的宏观反映。对比两个模型的电势和空间电荷密度得到的结果如图9所示。

图9 正负电晕的电势空间电荷密度Fig.9 Space charge density and potential of positive and negative corona

图9显示了通过自洽模型和简化模型获得的电势和空间电荷密度的空间分布。其中在图8中将负电晕的电势乘以-1,以便比较曲线形状。在正电晕的简化模型仿真中,对电极处的电场使用了皮克定律,没有添加源项。电势和空间电荷密度与通过等离子体模型获得的结果具有合理的一致性。差异主要归因于通过Peek定律获得的较低强度的电场。这一点在负电晕模型中得到了证明,这两个模型的仿真结果都非常吻合。

在简化的负电晕模型中,做了两个重要的更改以改善模型之间的一致性:内电极上的电场是从等离子体模型获得的电场,由于电子附着物在传输区域中非常重要,因此还添加了来自等离子体模型的载流子的源。

对比两个模型获得的电势和空间电荷密度结果:与稀有气体中的电晕放电相比,空气电晕放电需要更高的电压来击穿背景气体并维持放电。造成这种情况的主要原因有两个。首先是空气中的电子碰撞频率较高,其中部分是由于旋转和振动相互作用所致,使得电子加速更加困难,其次是空气中的氧带负电。

从上述结果可以看出,通过简化模型获得的空间电荷密度和电势与通过自洽等离子体模型获得的仿真结果非常吻合。