端直面齿轮弯曲应力的解析算法与实验

张宝玉, 孙铁波, 李德才, 李金华

(1.江苏食品药品职业技术学院 机电工程学院,江苏 淮安 223003,E-mail:20141013@jsfpc.edu.cn;2.东北林业大学 交通学院,哈尔滨 150040;3.辽宁工业大学 机械工程与自动化学院,辽宁 锦州 121001)

端直面齿轮传动以互换性好、结构紧凑、体积小、质量轻等巨大的传动优势,已在武器装备传动系统中得到了广泛应用。美国宇航局和美国军方先后资助了先进旋翼计划(ART、TRP)和旋翼机传动系统研究计划(RDS-21)等项目,已成功将端直面齿轮传动技术应用在阿帕奇武装直升机主减速器功率分流装置中,实现传动系统噪声降低10分贝,马力重量比提高35%,运行和维护费用降低20%的效果[1-3]。因此,越来越多的学者热衷于端直面齿轮传动技术的研究,而弯曲强度作为传动系统寿命的关键参数一直是研究的重中之重。

GUINGAND等人[4]基于FACET计划分析计算了端直面齿轮接触强度、啮合刚度、传动误差等传动要素,并采用实验的手段测试了最小内径处的弯曲应力。CLAUDIO等人[5]采用有限网格法研究了修形端直面齿轮在一个完整啮合周期内的弯曲应力的变化规律。Litvin等人[6]等研究了采用含齿顶圆角的蜗杆刀具加工端直面齿轮的方法,实现弯曲应力降低10%。ULRICH等人[7]比较了锥齿轮、齿条弯曲应力的计算数据,提出采用ISO6336计算端直面齿轮弯曲应力的方式,并推测了最小的齿根弯曲疲劳。黄丽娟等人[8]采用有限元手段分析了不同结构参数下斜齿面齿轮在齿顶加载时弯曲应力变化规律。付学中等人[9]建立了非正交偏置的一般性直齿面齿轮双分支传动系统的静力学扭矩分配模型,给出了静态均载系数的计算方法。张淑艳等人[10]推导了双压力角非对称齿形面齿轮的齿面方程,并通过有限元非对称齿 形设计可以获得更高的轮齿强度。户立杰等人[11]利用有限元软件分析实际工况下该对齿轮副的接触情况和传动特性,为后续面齿轮传动系统的优化设计及传动强度校核提供实验指导和理论依据。林菁等人[12]提出的基于齿面法矢量的直齿锥齿轮可展曲面齿面及其几何特性求解方法简单实用为直齿锥齿轮的创新设计提供了一种新方法和新途径。沈瑞等人[13]针对直齿轮多工况使用情况,研究了小轮修形齿面理论建模方法和直齿轮传动多工况多目标修形优化方法。

根据国外内文献综述,研究人员普遍采用的有限元仿真的方法获取端直面齿轮传动弯曲应力。但通过解析法计算端直面齿轮接触强度,尚未形成成熟的理论和方法。因此,开展端直面齿轮弯曲应力解析算法的研究十分有价值和意义。

本文基于锥齿轮构建了端直面齿轮当量齿轮,推导并建立了齿形系数、应力修正系数、重合度系数以及端直面齿轮当量齿轮弯曲应力计算公式,并通过实验手段对弯曲应力算法进行了验证,以期为端直面齿轮优化设计和在相关领域的应用研究提供了理论基础。

1 基于锥齿轮的端直面齿轮当量齿轮

▲图1 端直面齿轮的当量齿轮

端直面齿轮传动作为锥齿轮传动的特殊形式,如图1所示。因此在计算端直面齿轮强度时,借鉴锥齿轮当量理论,首先对端直面齿轮进行当量处理。

根据锥齿轮当量理论,端直面齿轮和小齿轮的节锥角计算公式为[15]:

(1)

根据锥齿轮当量理论,端直面齿轮和小齿轮的当量齿数计算公式为:

(2)

式中:γ为端直面齿轮传动的轴夹角;m12为传动比;N1和N2分别为为小齿轮和端直面齿轮的齿数;Nv1和Nv2分别为小齿轮和端直面齿轮的当量齿数。

端直面齿轮当量重合度计算[16]:

(3)

式中:αa1和αa2分别为当量小齿轮和端直面齿轮齿顶圆压力角,有:

(4)

式中:rbi和rai分别为齿轮基圆和齿顶圆半径。

2 端直面齿轮弯曲应力的计算方法

端直面齿轮当量齿轮弯曲应σ计算公式[17]为:

(5)

式中:YF为齿形系数;YS为应力修正系数;Yε为重合度系数。

(1) 齿形系数YF计算:

(6)

式中:S为危险齿厚;ha为弯曲力臂;αFen为载荷作用角。

载荷作用角αFen为:

αFen=αet-γ

(7)

(8)

式中:x为变位系数。

(ⅰ) 危险齿厚S的计算原理为采用30°切线法确定危险截面的危险齿厚:

(9)

式中:θ为滚动切线角;ρ为刀具齿顶圆角半径。

由齿条刀具加工的小齿轮可知,各参数存在以下关系:

(10)

(11)

(12)

(13)

(14)

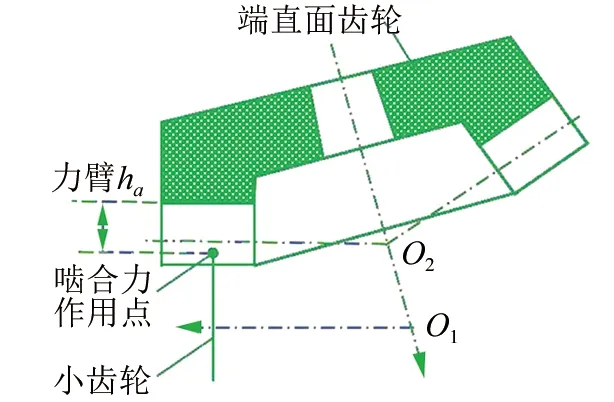
▲图2 面齿轮弯曲应力力臂计算方法

(ⅱ) 弯曲力臂ha的计算原理是利用LTCA分析来计算齿面接触点坐标,通过齿面接触点坐标确定力臂大小,如图2所示。

则弯曲应力力臂ha的计算公式为:

ha=z-zmin

(15)

(2) 应力修正系数YS的计算公式为:

(16)

式中:ρF为齿根处的曲率半径,由端直面齿轮TCA分析程序获取。

(3) 重合度系数Yε的计算公式为:

(17)

式中:ε为重合度。

3 算法验证及应用研究

3.1 算法实验验证

对弯曲应力算法准确性进行实验验证,选取的端直面齿轮传动参数如表1所示。

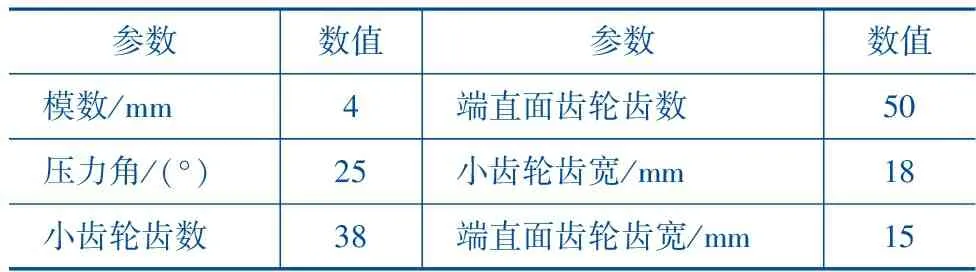
表1 端直面齿轮传动设计参数

根据公式(7)、(17)和(18),输入表1及载荷数据(扭矩为1 005 N·m),计算随着两齿轮旋转啮合点位置变化的齿形参数、应力修正系数和重合度系数数值如表2所示。其中,端直面齿轮每旋转7.2°计算一次数据。

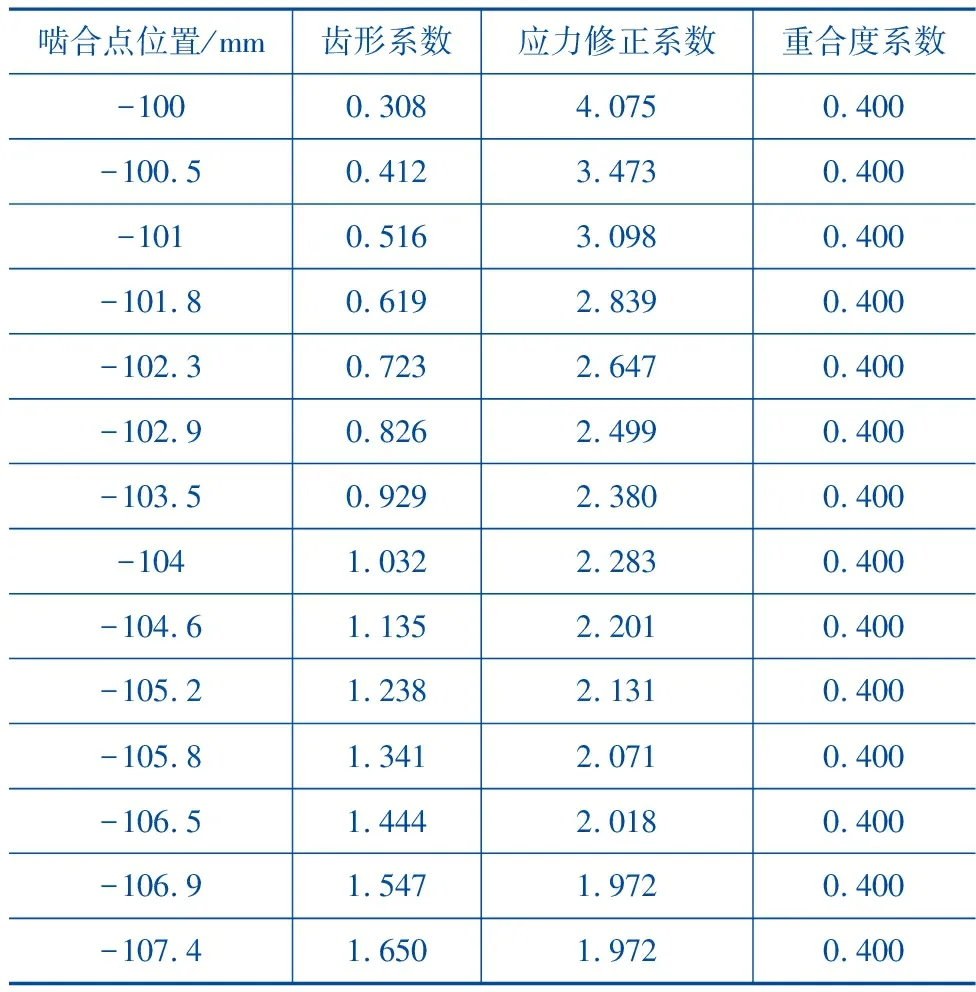
表2 弯曲应力解析法中间变量计算结果

将上述数据代入公式(6),获得端直面齿轮弯曲应力的数据如图3所示。

选中表1中相应端直面齿轮的样件,开展端直面齿轮传动弯曲应力实际检测实验。采用的是相交轴滚动检查试验台,如图4所示。其中,应变片是通过导电滑环输出信号。

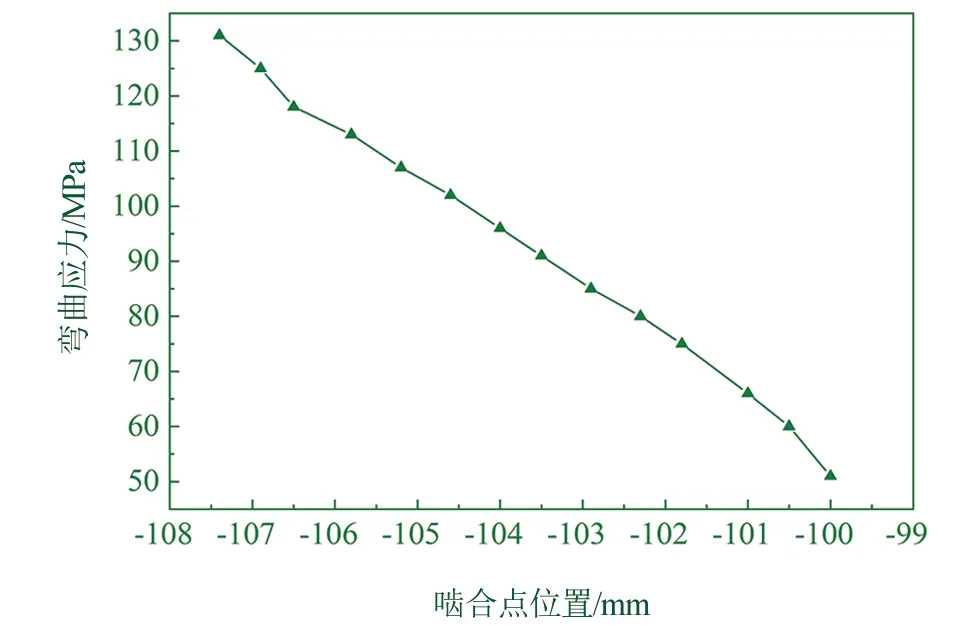
▲图3 端直面齿轮弯曲应力曲线图

▲图4 端直面齿轮传动弯曲强度试验

通过上述试验台,设定旋转角度和载荷,获取的端直面齿轮弯曲应力的数据如表3所示。其中,端直面齿轮有效弯曲应力数据采取三次测量取平均值的方法进行,端直面齿轮弯曲应力计算值由图3的计算程序导出。

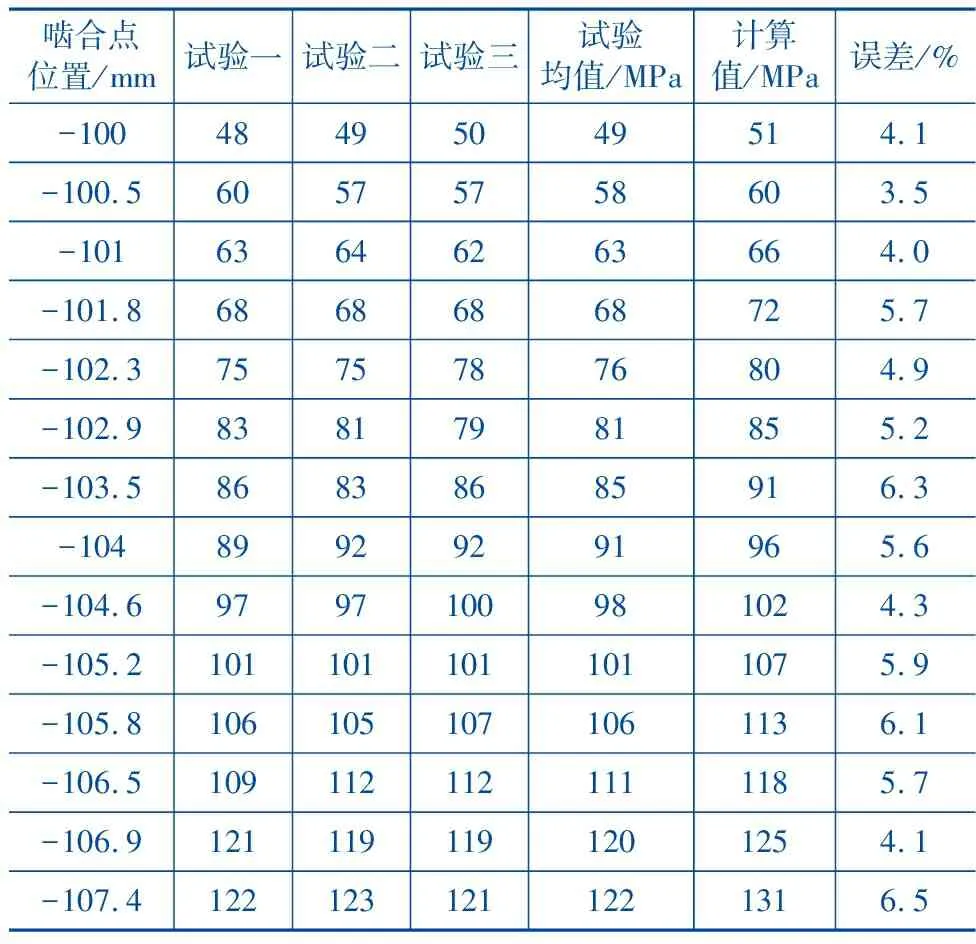
表3 弯曲应力实验结果及计算结果对比

从表3中可知,端直面齿轮弯曲应力的计算结果与实验结果随啮合点位置变化趋势一致,最大误差为6.5%,最小误差为3.5%。总体误差在7%在合理范围之内,验证了该算法的可靠性和准确性。

3.2 算法应用研究

3.2.1 模数对弯曲应力计算结果的影响

分别选取模数m=5、m=6,压力角a=30°,齿数比38∶50,变位系数x=0的端直面齿轮进行弯曲应力计算,计算结果如图5所示。

由图5曲线可知,增大端直面齿轮模数,端直面齿轮弯曲应力明显减小。

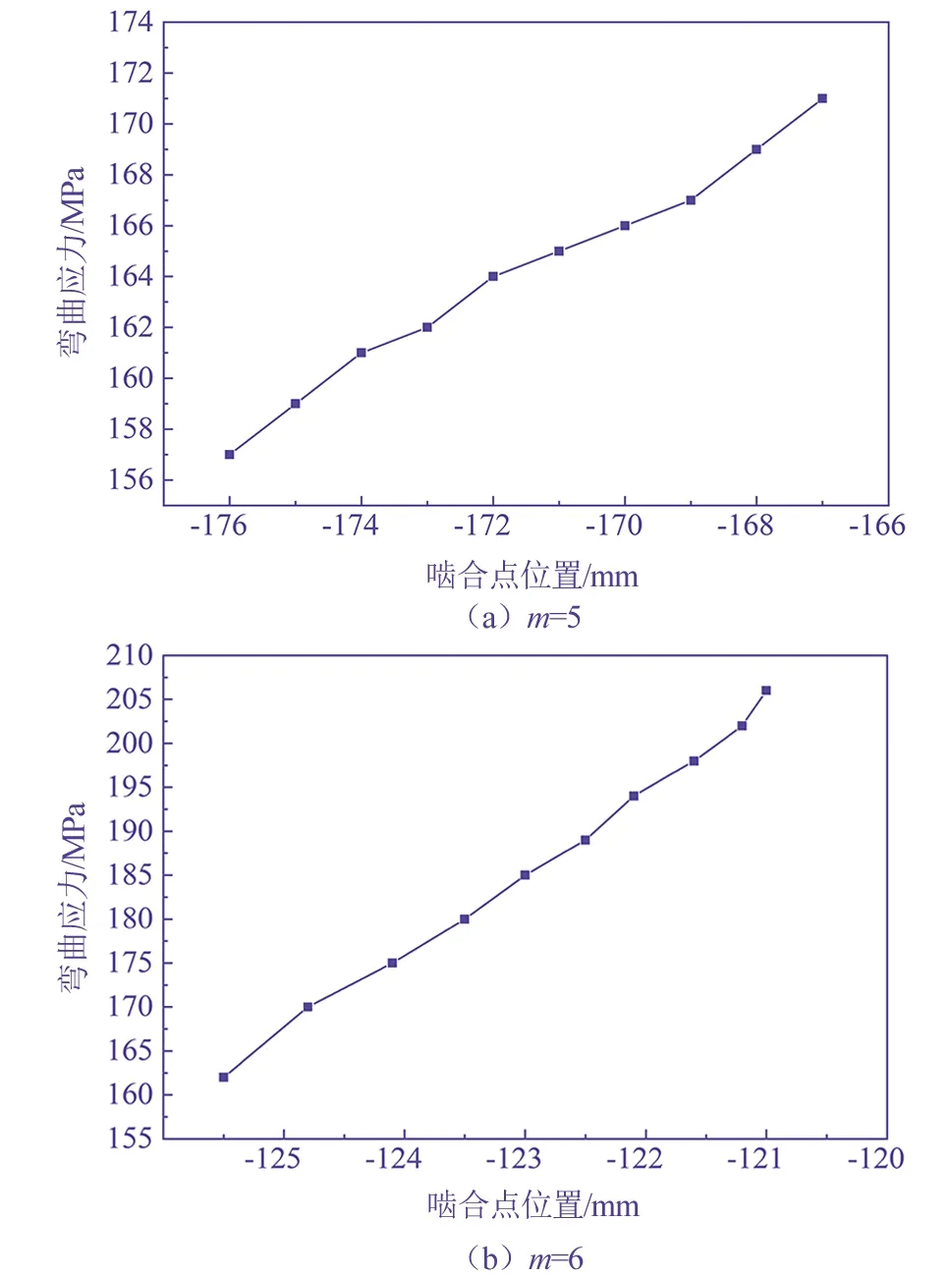
▲图5 不同模数的端直面齿轮弯曲应力

3.2.2 变位系数对弯曲应力计算结果的影响

选取变位系数x=0.1、x=0.2,压力角a=30°,齿数比38∶50,模数m=5的端直面齿轮进行弯曲应力计算,结果如图6所示。

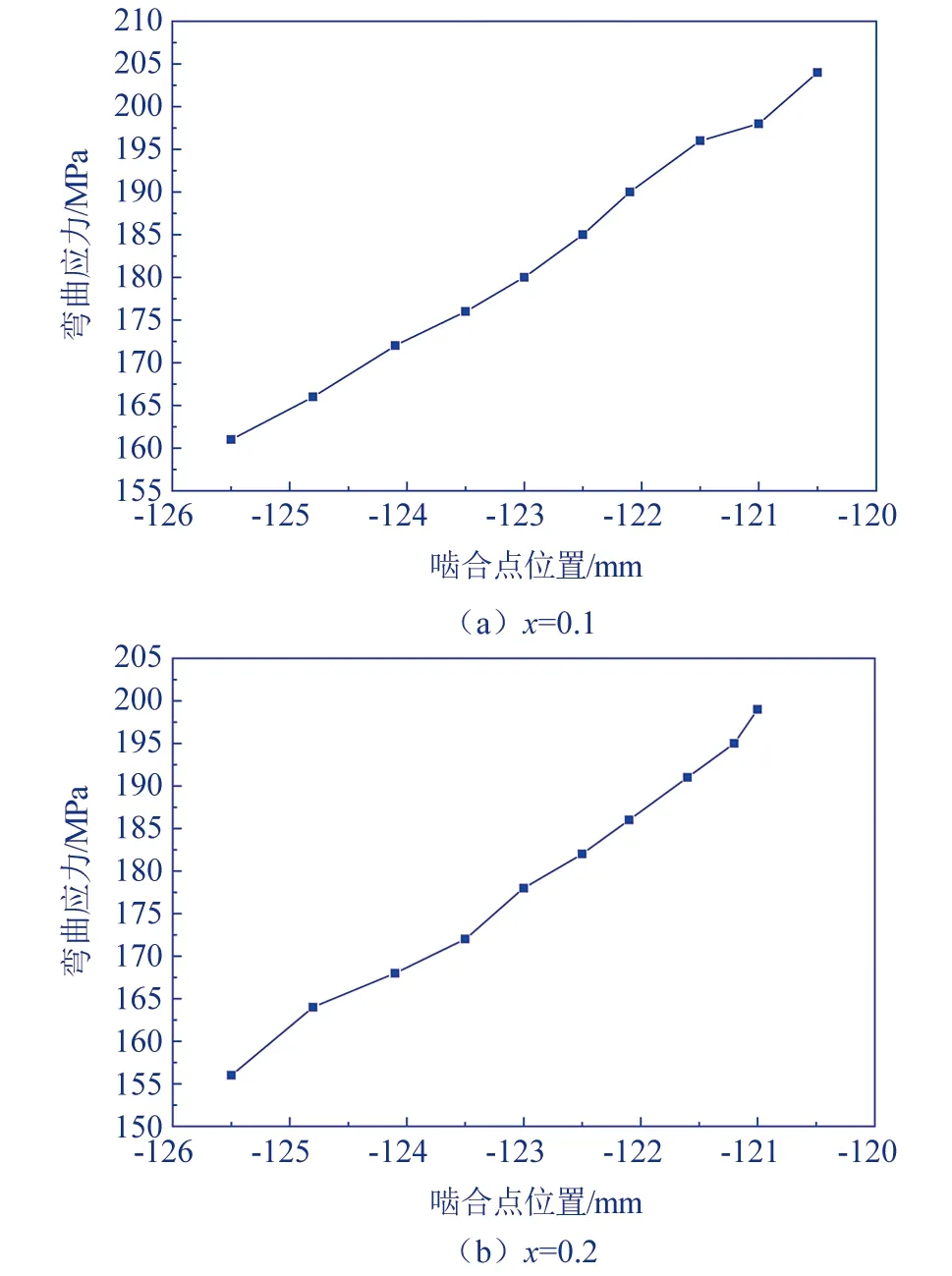
▲图6 不同变位系数端直面齿轮弯曲应力

由图6可知,采取正变位可以减小弯曲应力,提高承载能力,但效果有限。

3.2.2 压力角对弯曲应力计算结果的影响

选取压力角分别是25°、28°,齿数比38∶50,模数m=5,变位系数x=0的端直面齿轮进行弯曲应力计算,结果如图7所示。

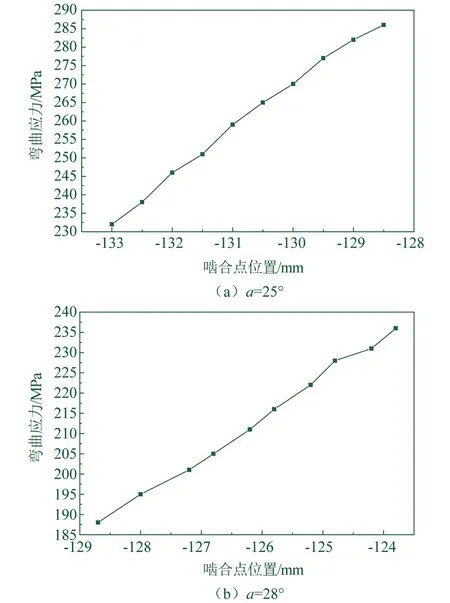
▲图7 不同压力角端直面齿轮弯曲应力

由图7可知,压力角增大弯曲应力有所减小,承载能力提高。

3.2.4 齿轮参数对弯曲应力的权重分析

设计正交实验,开展模数、压力角和变位系数对端直面齿轮弯曲应力的权重分析,计算结果分析如表4所示。

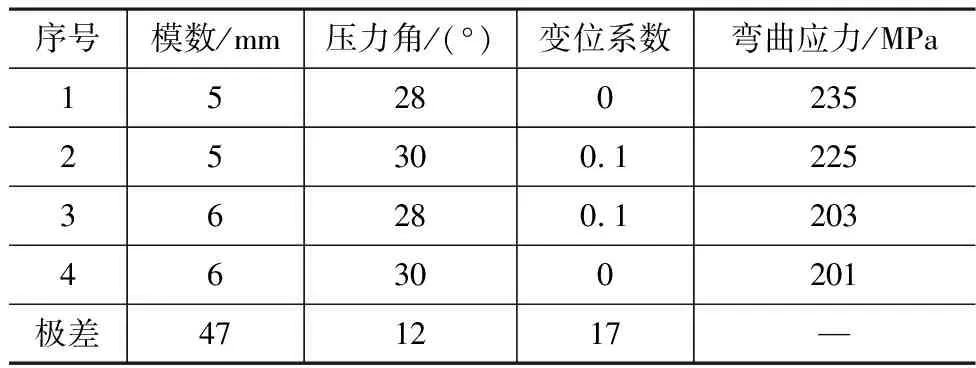
表4 正交实验数据及分析

通过表4正交实验数据,模数的极差最大,变位系数次之,压力角最小。由此可见,模数对端直面齿轮弯曲应力影响最大。因此,当面齿轮弯曲应力明显不足时,应优先提高端直面齿轮的模数。

4 结论

构建了端直面齿轮当量齿轮,建立了端直面齿轮弯曲应力计算公式,通过实验验证了该算法的准确性,并分析了齿轮参数对弯曲应力的影响权重,得到如下结论:

(1) 根据端直面齿轮为零度锥齿轮的定义,将锥齿轮当量引入端直面齿轮理论体系,构建了端直面齿轮当量齿轮。

(2) 基于材料强度理论,推导了齿形系数、应力修正系数和重合度系数的计算公式,建立了端直面齿轮当量齿轮的弯曲应力计算公式。

(3) 通过台架实验,获得一个周期内弯曲应力计算结果与实测结果误差在7%以内,验证了该算法的可靠性和准确度。

(4) 基于该算法,分析了齿轮参数对端直面齿轮弯曲应力的影响规律,发现模数对端直面齿轮弯曲应力影响最大,变位系数次之,压力角最小。