基于贝叶斯网络的机械产品再设计构件变更概率研究

王琪旸, 邓益民

(1.宁波大学 机械工程与力学学院,浙江 宁波 315211,E-mail:18868975865@163.com;2.浙江省零件轧制成型技术研究重点实验室,浙江 宁波 315211)

在机械产品的设计开发过程中,设计人员通常需要在现有产品或设计的基础上通过再设计进行修改、变更,使得变更后的产品可以满足新的设计任务要求。但是,由于系统构件之间的关联性,对目标结构的变更修改可能会导致与该目标结构直接或间接关联的其他系统构件受到影响,从而需要被迫进行相应的变更,即造成了变更传播。产品结构的被迫或被动变更会增加设计成本,导致设计过程复杂化,延长产品的设计开发周期,因此有必要对再设计中产品各构件的变更风险进行量化评估。

目前,已有一些针对变更传播的相关研究,如李玉鹏等[1]将复杂网络理论应用于复杂产品构件建模中,从构件自身属性、网络拓扑属性、变更影响属性等方面建立了构件重要度评价体系;殷习等[2]基于“功能-行为-结构”(FBS)模型对构件约束关系进行分析,制定了构件关联强度的量化值,建立构件关联矩阵以描述构件之间变更传播的可能性;王秋月等[3]根据构件之间的关联关系建立网络模型,采用功能关联度、变更传播指数等评估变更影响强度。上述研究在对构件变更风险进行量化评估时,部分指标的量化值是根据专家经验给出,人为参与的主观性较强。由于构件的变更概率是衡量变更风险的重要因素,根据企业的历史变更数据进行分析,通过科学的推理得到各构件的变更概率则可以很好的减少主观性;但目前对于满足新设计任务要求的前提下构件的变更概率的计算问题尚没有针对性的研究,因此有必要对其开展研究。

针对上述问题,考虑到贝叶斯网有着强大的推理能力及参数学习能力,本文引入贝叶斯网对构件的变更概率进行计算,从变更概率的角度对构件的变更风险进行量化评估,以对变更风险进行及时的识别和防范,指导机械产品的设计开发及生产管理的过程。

1 问题分析

1.1 构件变更概率的计算

在机械产品再设计的过程中,设计人员需要根据新的设计任务要求,确定需要变更和需要保留的构件,并以此作为条件,考虑变更传播,分析其他构件受变更传播的影响情况。其中,有关变更影响的重要数据之一是“变更概率”[4]。有了变更概率,设计人员就可以分析不同变更设计方案的影响范围,进而分析各方案的设计复杂度,因此可以帮助设计人员正确进行设计决策。有关各构件的变更情况可以用一组随机变量描述,每个变量都有两个取值“1”或“0”,其中,“1”表示构件发生变更,“0”表示构件不发生变更。根据新的设计任务要求,可确定部分构件的变更情况,即已知部分变量的取值,这些已知的变量分别记为X1,X2,…,其取值分别为x1,x2,…,需要计算后验概率的变量记为Y。根据条件概率分布公式可得满足新设计任务要求时构件的变更概率

通过查询这些变量的联合分布表,利用边缘分布即可求得各构件的变更概率。但联合分布的复杂度随着变量数的增加呈指数增长,这时需要非常庞大的数据才能进行可靠的推理。由于大多数机械产品构件数较多,联合分布的数值通常难以获取,推理过程十分困难,为此本文将引入贝叶斯网以降低推理的复杂度。

1.2 贝叶斯网

贝叶斯网是一种基于概率推理的图形化网络,由节点和有向边构成,其中节点表示变量,有向边表示变量间的关联关系。通过对变量间关联关系进行分析,依据变量之间的条件独立性,可以构建起贝叶斯网,将联合分布分解,使复杂的推理变得可行[5]。

贝叶斯网的推理很大程度上依赖于变量之间的关联关系,其中,变量间的关联强度决定了贝叶斯网络的条件概率分布,变量的顺序决定了推理的复杂度。因此,本文将先对构件间的关联性进行研究,建立网络模型以描述构件间的关联关系,以此作为参考确定贝叶斯网的结构。

2 机械产品的构件关联性分析

2.1 机械产品构件间的关联关系

机械产品构件网络模型是产品相关设计信息的具体表达,其中,网络节点表示机械产品的构件,连边表示构件间的关联关系。由于构件间的关联关系错综复杂,在构建机械产品构件网络模型时,如果只考虑构件间直观的的物理联接关系,则会忽略一些重要的设计信息,这样构建出的网络模型无法准确地反映机械产品构件之间的关联性,例如数控车床的主轴传动机构和横、纵向进给机构由多台伺服电机独立控制,通过数控装置实现精确的关联,以完成圆弧插补等高精度的加工功能,尽管主轴传动机构和横、纵向进给机构在结构上并没有直接的物理联接关系。

因此,研究该模型需要首先对产品设计信息进行详细的研究和分析。考虑到FBS(功能-行为-结构)模型[6]对产品概念设计阶段相关设计信息的完整表达特性以及对实施设计过程的作用,本文将在FBS模型的基础上开展机械产品构件关联性的研究。

在FBS理论中,功能层、行为层、结构层之间存在映射关系,如图1所示。其中,结构是行为的载体,是行为的执行者;行为是结构在实现其相应功能时所呈现的物理状态或状态改变[7],是功能的实现方式;功能是一系列行为的目的性抽象。FBS理论根据产品功能、行为和结构之间的映射关系,对产品概念设计设计的过程进行了细分,实现了抽象的功能在结构上的具体化落实。

▲图1 功能-行为-结构映射

类似地,构件之间的关联关系可以分为结构上的直接关联关系和功能、行为上的间接关联关系[8]。结构上的关联关系具有直观性,表现为两结构体之间存在着直接的物理联接;功能、行为上的关联关系具有隐蔽性,根据FBS理论,这种关联关系往往是通过“功能-行为-结构”的映射关系间接表现出来的,例如普通车床在实现螺纹加工功能时,横、纵向进给机构和主轴传动机构存在着功能上的关联关系,这种功能上的关联关系可以映射为行为上的关联关系:即加工时需保持一定的主轴转速和横向进给速度,而行为上的约束关系可以进一步映射到结构上:即通过一定传动比的传动机构来实现相应的行为。

下文将分别对这三种关联关系的关联方向和关联强度进行分析,在综合考虑这三种关联关系的基础上建立机械产品构件网络模型。

2.2 结构关联性分析

机械产品构件间的结构关联性表现为构件之间的物理联接关系,可以直接根据产品的BOM(物料清单)进行确认。结构关联方向由构件自身指向受其约束的其他构件,可根据构件间的约束情况和装配情况确定。构件之间的物理联接形式决定了结构关联强度,通过焊接、粘合等方式固定的两个构件间的结构关联强度最高,在发生设计变更时最有可能出现变更传播;通过形位配合方式联接的构件之间结构关联强度较高;通过限位等方式联接的构件之间结构关联强度较低。

结构层包含的设计信息更多的是产品的几何参数、物理参数等,而行为作为功能和结构的连接纽带,包含更复杂的关联关系,下文将对行为关联性进行分析。

2.3 行为关联性分析

机械产品的行为关联性跟“流”有关,流是机械产品在工作过程中能量、信息和物料的传递与转化过程。根据系统设计理论[9],可以按介质种类将流分为三种基本类型:能量流、信息流和物料流。

流决定了机械产品构件间的行为关联方向。机械产品的行为互相配合,按照一定的逻辑顺序执行,以实现机械产品的不同功能,这些行为的组合称为行为链[10],组成行为链的各个行为称为行为元。根据行为元执行的逻辑顺序,可将行为链分为顺连、分连和汇连三种基本类型,如图2所示,实际机械产品的行为链可能是这三类基本行为链的组合。行为的执行方向与流的方向一致,因此行为关联方向可以根据行为链的方向确定。

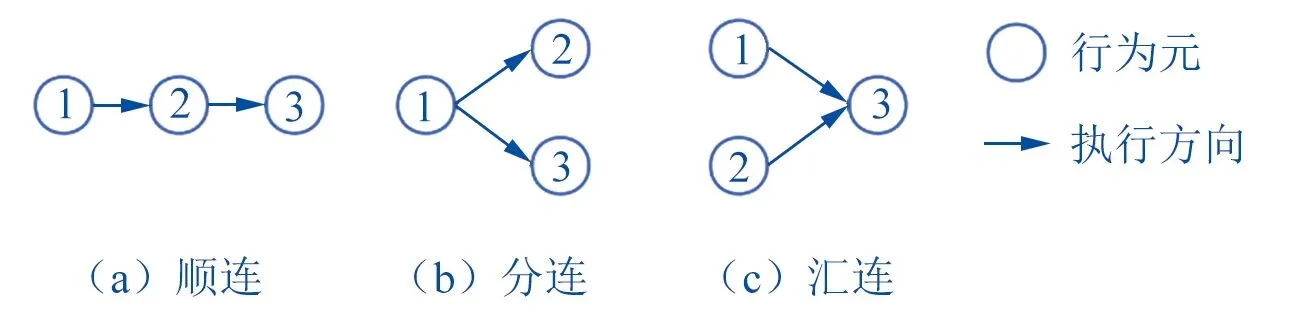
▲图2 行为链的类型

流也决定了机械产品构件间的行为关联强度。一般认为能量流直接作用于机械产品的工作功能,信息流辅助工作功能的实现,物料流反映了工作功能的结果。因此存在能量流的传递时,构件之间的关联强度较高,信息流次之,物料流最低。

2.4 功能关联性分析

根据FBS理论,机械产品的行为和功能之间存在映射关系,功能是一系列行为的组合,因此构件间的功能关联性同样是由流决定,功能关联方向不必重复确定。

机械产品构件间的功能关联强度表现为流传递的频率。机械产品构件可以根据产品的子功能划分为多个功能模块。根据模块的划分准则,功能模块应具备功能独立性,即应将功能关联性最高、交互作用最强的构件组划分为一个模块,并减少模块之间的交互作用[11]。因此,同个功能模块内的构件之间流的传递更加频繁,构件之间的功能关联性更强,变更传播的概率更高。

2.5 机械产品构件网络模型

网络模型可以用有向图表示,其中V是有向图中所有节点的集合,用于表示系统的基本组成元素,E是节点间连边的集合,用于表示节点间的相互作用。在对机械产品构件建立网络模型时,应综合考虑构件间结构、行为、功能三个层面的关联关系[12-15],根据关联方向将节点相互连接,即可构建起有向网络。

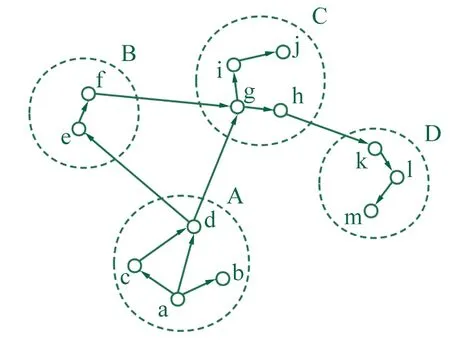
▲图3 机械产品构件的二级网络模型

由于同个功能模块内的构件之间关联关系更加密切,网络节点存在明显的集聚性,因此可以采用二级网络模型来表示。如图3所示,该机械产品由四个功能模块组成,分别与网络节点A、B、C、D对应,这些节点称为一级节点,一级节点之间通过一级连边连接。每个一级节点又由多个基础节点(a、b、c等)组成,这些基础节点称为二级节点,即组成机械产品的基本构件,二级节点通过二级连边连接。可以看出,采用二级网络模型对机械产品进行建模,构件之间关联关系的描述非常清晰直观。

3 基于贝叶斯网的查询推理

3.1 变量及变量取值的确定

贝叶斯网的构建包括三个过程:变量及变量取值的确定、结构选择和参数学习。在贝叶斯网的构建之初,选择合适的变量来描述问题,并为变量确定取值,对整个推理过程起着重要的作用。在机械产品构件变更概率判断问题中,可以将每个构件的变更情况视为一个随机变量,分别用字母A、B、C等表示,每个变量都有“1”或“0”两个取值,其中,“1”表示构件发生变更,“0”表示构件不发生变更。这样,机械产品的变更决策情况就可以用这组随机变量加以描述。

3.2 贝叶斯网的结构选择

在构建贝叶斯网时,变量添加的顺序可以随机设定,顺序不同,构建出的贝叶斯网的结构也不尽相同。在贝叶斯网中,子节点的概率分布和指向它的父节点有关,网络的边越多,计算的过程越复杂。为了获得较为简单的网络结构,通常根据变量之间的逻辑关系确定。

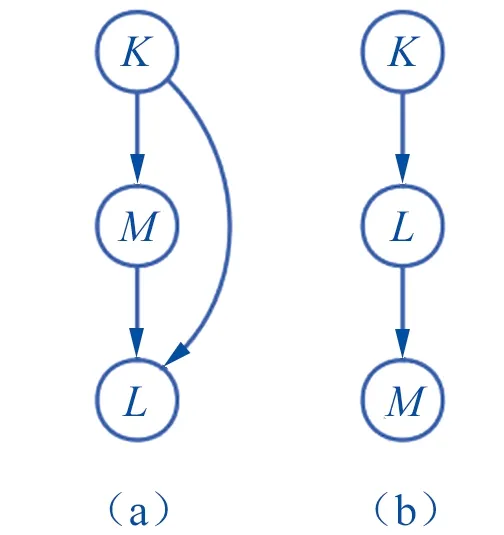
▲图4 不同变量顺序得到的贝叶斯网结构

以图3中的一级节点D为例,该节点包括3个二级节点k、l、m,他们的变更情况分别用K、M、L表示。若以顺序α1=〈K,M,L〉对这三个节点的变更情况构建贝叶斯网,在加入M时,由于不知道构件l的变更情况,构件k的变更有可能会引起l的变更,无法确定K和M互相独立,因此K和M之间需用有向边连接;加入L时,K和M的取值都对L产生影响,因此构建出的网络结构如图4(a)所示。若参考构件之间的关联方向,以顺序α2=〈K,L,M〉对这3三个节点的变更情况构建贝叶斯网,在加入L时,L依赖于K,K和L之间用有向边连接;在加入M时,根据条件独立性,在构件l的变更情况已知的情况下,M的取值只与L有关,因此构建出的网络结构如图4(b)所示,该网络的边更少,在对联合分布化简时可以减少参数的个数,有效地降低推理运算的复杂度。

因此,在确定贝叶斯网结构时,可以参考机械产品构件的网络模型,以网络模型中的根节点对应的变量作为起点,按网络模型中有向边的顺序添加变量,即可得到较为简单的贝叶斯网结构。

3.3 贝叶斯网的参数学习

贝叶斯网的参数是指节点依附的条件概率表(CPT),具体来说,根节点依附的是边缘分布,非根节点的取值依赖于其父节点,因此非根节点依附的是条件概率分布。CPT可以反映变量之间的关联强度。

在数据不足的情况下,CPT可以通过专家咨询,根据专家经验得到。虽然从定性的角度可知,构件之间的关联性越强,变更传播的概率越大,但由于人的认知水平有限,人工参与的主观性太强,若根据变量之间的关联强度定量地确定贝叶斯网的参数,推理结果的准确度较低,且需要耗费很多的时间和人力。

在数据充足的情况下,通过数据分析可以得到精确度极高的参数。企业的机械产品变更历史数据库记录着每种变更事件对应的变量组的取值,将这些样本数据载入MATLAB中,使用BNT工具箱中的最大似然估计算法进行参数学习,即可得到真实性很高的CPT。

3.4 查询推理

机械产品各构件的变更概率可通过查询推理求得。根据设计变更的要求,可以确定部分构件的变更情况,其中包括为了实现新的设计任务要求必须保留的构件和必须变更的构件,这些构件对应的变量称为证据变量,记为E,其取值为e;需要计算后验概率的变量称为查询变量,记为Q;各构件在满足设计任务要求的条件下的变更概率就是P(Q=1|E=e))。

查询推理可以用于多种因果推理情形,以图4(b)的贝叶斯网为例,查询推理可用于多种推理情形,包括正向推理P(L=1|)K=1)反向推理P(L=1|)M=1)及混合推理P(L=1|)K=0,M=1)等。这些后验概率可以用变量消元算法求得,但由于在实际应用中,需要分别计算多个构件的变更概率概率或多种条件下某一构件的变更概率,使用变量消元法进行计算会有大量重复的计算过程,而使用BNT工具箱中的联合树推理引擎进行计算能提高计算效率,大幅减少工作量。

4 实例分析

如今,共享单车以方便、环保的优点,成为了城市居民出行的重要代步工具,用户规模日益增长。某品牌旗下的共享单车主要由12种构件组成,包括一体成型的车架、车把、前叉、座杆、车座、链条、前牙盘、后牙盘、脚踏、曲柄连杆、前轮、后轮,按功能可以划分为三个主要的模块,包括转向模块、传动模块和支撑模块。现应市场环境和生产制造的需要,设计人员决定对车架进行重新设计,将其变结构更为简单、材质更为轻便的车架,出于成本考虑,前轮和后轮不进行变更。下文将以共享单车这一再设计所引起的变更传播问题为例,对其他构件的变更概率进行计算。

首先,根据产品的BOM确定构件之间的结构关联关系,并结合构件的行为关联性和功能关联性对产品构件建立二级网络模型,如图5所示。

设定变量A、B、C、…、G分别表示构件a、b、c、…、g的变更情况,在构建贝叶斯网时,参考共享单车构件的网络模型,选择根节点a对应的变量A作为起点,按网络模型中有向边的层级依次添加变量节点,根据构件间的关联性设定贝叶斯网的有向边,确定贝叶斯网的结构,如图6所示。

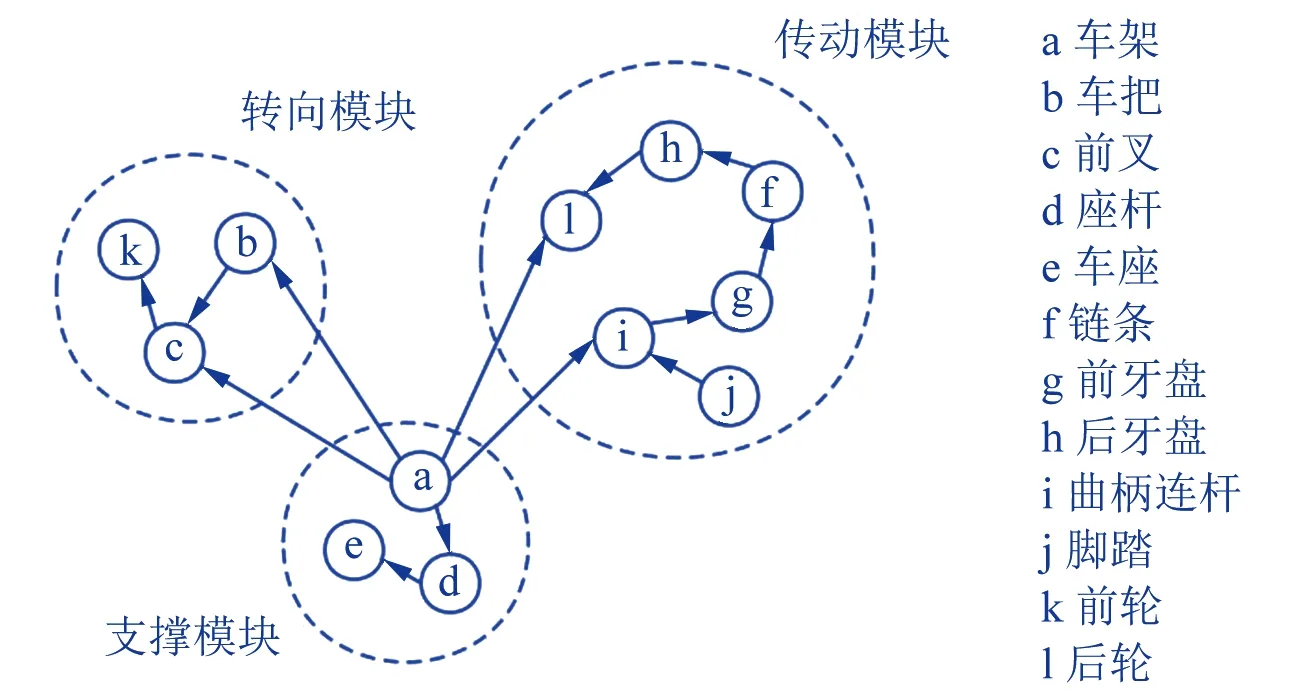
▲图5 共享单车构件的网络模型

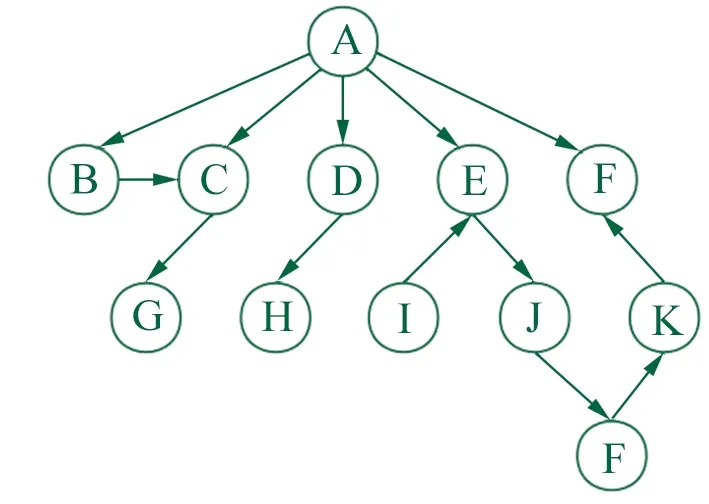
▲图6 贝叶斯网结构

查询某企业关于该产品的的历史变更数据,将数据导入MATLAB中,使用BNT工具箱中的最大似然估计算法进行参数学习,得到各变量依附的CPT如图7所示。

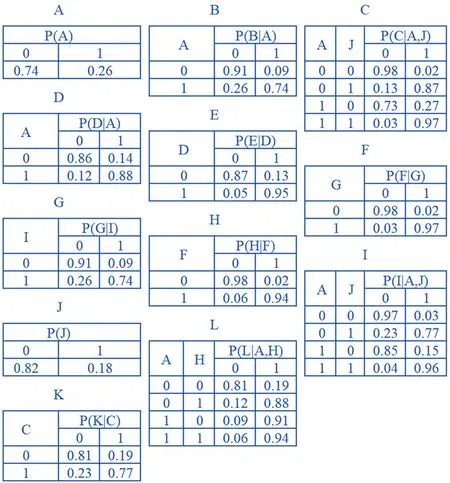
▲图7 各变量的条件概率分布表

根据新的设计任务要求,可知证据变量集E={A=1,K=0,L=0},借助BNT工具箱中的联合树推理引擎对该条件下各构件的变更概率P=(Q=|A)=1,K=0,L=0)进行计算,结果如表1所示。

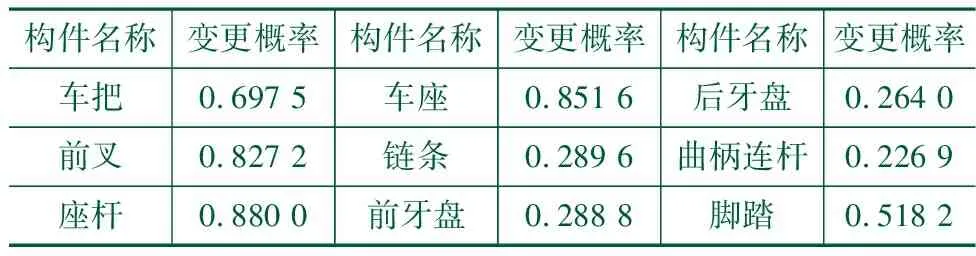
表1 各构件变更概率

由表1可以看出,受变更传播的影响,在车架发生设计变更,前轮和后轮不发生变更时,前叉、座杆及车座被迫进行变更的概率很高,再设计时应及时对这些构件的变更风险进行防范,并指导产品的生产管理过程。此外,由各构件的变更概率可以看出设计变更的影响范围,若设计开发中还有其他再设计方案,则设计人员可以类似地对各构件的变更概率进行计算,并对多种方案进行综合评估,总体概率较低者意味着其变更影响的范围较小,再设计复杂度较低,因此从一个方面为设计人员进行方案选择提供了决策依据。

5 结论

机械产品再设计的过程中,有必要考虑变更传播的影响,对构件的变更风险进行评估。本文提出了一种基于贝叶斯网的机械产品再设计构件变更概率计算方法,通过对构件间的关联关系的研究,建立机械产品构件二级网络模型,参考此模型,建立机械产品设计变更的贝叶斯网,并基于贝叶斯网的查询推理求得构件的变更概率。这一方法不仅可以将再设计中的变更传播影响加以量化,而且可以辅助设计人员对多种变更设计方案的优劣进行评判,从而为设计人员的设计决策提供依据。